2024年四川省成都市成华区中考数学二诊试卷（含解析）

这是一份2024年四川省成都市成华区中考数学二诊试卷（含解析），共30页。试卷主要包含了选择题．，填空题，解答题等内容，欢迎下载使用。

1．（4分）在π，﹣2，0，﹣1这四个实数中，最小的数是（ ）
A．πB．﹣2C．0D．﹣1
2．（4分）由一个长方体和一个圆柱组成的几何体如图所示，则这个几何体的俯视图是（ ）
A．B．
C．D．
3．（4分）经国家统计局初步核算，2023年我国国内生产总值1260582亿元，按不变价格计算，比上年增长5.2%．其中数据“1260582亿”用科学记数法表示为（ ）
A．1260582×108B．1.260582×1013
C．1.260582×1014D．1.260582×1015
4．（4分）下列运算中，计算正确的是（ ）
A．（a2b）3＝a6b3B．5a﹣3a＝2
C．（a+b）2＝a2+b2D．a6÷a3＝a2
5．（4分）为了解学生参加体育锻炼的情况，从该班学生中随机抽取5名同学进行调查．经统计，他们的体育锻炼时间（单位：分钟）分别为：65，60，75，60，80．则这组数据的众数是（ ）
A．60B．65C．75D．80
6．（4分）如图，直线m∥n，△ABC是等边三角形，顶点B在直线n上，直线m交AB于点E，交AC于点F，若∠1＝140°，则∠2的度数是（ ）
A．110°B．105°C．100°D．95°
7．（4分）如图，△ABC内接于⊙O，CD是⊙O的直径，若∠DCA＝38°，则∠ABC＝（ ）
A．56°B．52°C．48°D．38°
8．（4分）如图，二次函数y＝ax2+bx（a＜0）的图象过点A（2，0），下列结论错误的是（ ）
A．b＞0
B．a+b＞0
C．x＝2是关于x的方程ax2+bx＝0（a＜0）的一个根
D．若点（x1，y1），（x2，y2）在二次函数的图象上，且x1＞x2＞2，则y2＜y1＜0
二、填空题（本大题共5个小题，每小题4分，共20分）
9．（4分）分解因式：ab2﹣2ab+a＝ ．
10．（4分）如图，以正五边形ABCDE的顶点C为旋转中心，按顺时针方向旋转，使得新五边形A′B′CD′E′的顶点D′落在BC 的延长线上，则正五边ABCDE旋转的最小度数为 ．
11．（4分）若直线y＝x向上平移3个单位长度后经过点（2，m），则m的值为 ．
12．（4分）元朝朱世杰的《算学启蒙》一书记载：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之．”其题意为：“良马每天行240里，劣马每天行150里，劣马先行12天，良马要几天追上劣马？”答：良马追上劣马需要的天数是 ．
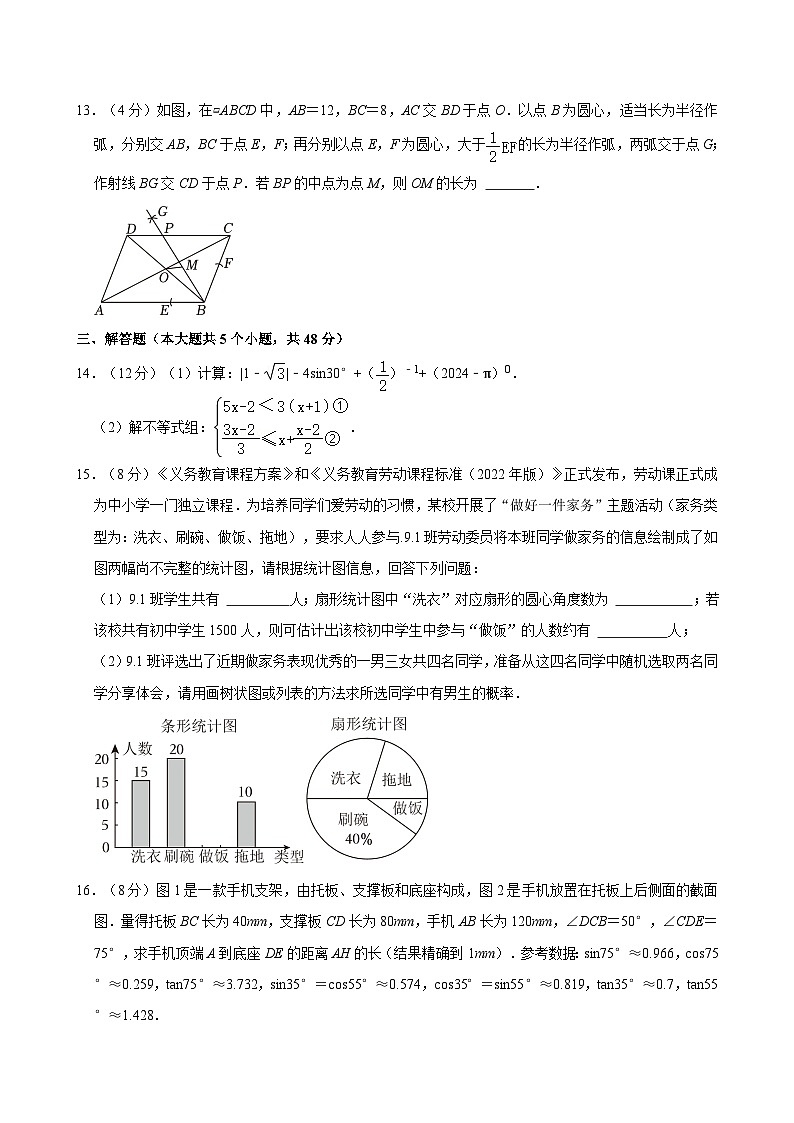
13．（4分）如图，在▱ABCD中，AB＝12，BC＝8，AC交BD于点O．以点B为圆心，适当长为半径作弧，分别交AB，BC于点E，F；再分别以点E，F为圆心，大于的长为半径作弧，两弧交于点G；作射线BG交CD于点P．若BP的中点为点M，则OM的长为 ．
三、解答题（本大题共5个小题，共48分）
14．（12分）（1）计算：|1﹣|﹣4sin30°+（）﹣1+（2024﹣π）0．
（2）解不等式组：．
15．（8分）《义务教育课程方案》和《义务教育劳动课程标准（2022年版）》正式发布，劳动课正式成为中小学一门独立课程．为培养同学们爱劳动的习惯，某校开展了“做好一件家务”主题活动（家务类型为：洗衣、刷碗、做饭、拖地），要求人人参与.9.1班劳动委员将本班同学做家务的信息绘制成了如图两幅尚不完整的统计图，请根据统计图信息，回答下列问题：
（1）9.1班学生共有 人；扇形统计图中“洗衣”对应扇形的圆心角度数为 ；若该校共有初中学生1500人，则可估计出该校初中学生中参与“做饭”的人数约有 人；
（2）9.1班评选出了近期做家务表现优秀的一男三女共四名同学，准备从这四名同学中随机选取两名同学分享体会，请用画树状图或列表的方法求所选同学中有男生的概率．
16．（8分）图1是一款手机支架，由托板、支撑板和底座构成，图2是手机放置在托板上后侧面的截面图．量得托板BC长为40mm，支撑板CD长为80mm，手机AB长为120mm，∠DCB＝50°，∠CDE＝75°，求手机顶端A到底座DE的距离AH的长（结果精确到1mm）．参考数据：sin75°≈0.966，cs75°≈0.259，tan75°≈3.732，sin35°＝cs55°≈0.574，cs35°＝sin55°≈0.819，tan35°≈0.7，tan55°≈1.428．
17．（10分）如图，AB为⊙O的直径，C是下半圆弧的中点，D为半径OA（除端点外）上一点，CD的延长线交⊙O于点E，过点E作⊙O的切线交BA的延长线于点F．
（1）求证：FD＝FE；
（2）若BD＝7，，求⊙O的半径及tanF的值．
18．（10分）如图，一次函数y＝x+2的图象与反比例函数y＝（x＞0）的图象交于点A（a，3），与y轴交于点B．
（1）求反比例函数的解析式；
（2）若C为反比例函数y＝（x＞0）图象上一点，直线AC与x轴交于点D，且满足AD＝2AC，求点C的坐标．
（3）若点P在反比例函数y＝（x＞0）图象上，点Q在x轴上，且以点A，B，P，Q为顶点的四边形是平行四边形，请直接写出符合条件的点P的坐标．
一、填空题（本大题共5个小题，每小题4分，共20分）
19．（4分）若m、n满足3m﹣n﹣4＝0，则8m÷2n＝ ．
20．（4分）《墨子•天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，以面积为4的正方形ABCD的中心O为位似中心，作它的位似图形A′B′C′D′，若A′B′：AB＝2：1，则四边形A′B′CD′的外接圆的面积为 ．
21．（4分）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点P为BC边上一动点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长的最小值为 ．
22．（4分）数学综合与实践活动小组用四个全等的直角三角形（Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA）拼成如图所示的“赵爽弦图”，得到正方形ABCD和正方形EFGH，连接AC和EG，AC与DF，EG，BH分别相交于点P，O，Q．若，则的值是 ．
23．（4分）若点M（x，y）的坐标满足x2＝t﹣5y，y2＝t﹣5x，其中x≠y，t为常数，则称点M为“好点”．若双曲线 上存在“好点”，则k的取值范围是 ．
二、解答题（本大题共3个小题，共30分）
24．（8分）某校为落实立德树人的根本任务，积极探索“五育并举，融合育人”的育人途径，计划组织八年级师生租用客车到成都大熊猫基地开展跨学科主题研学活动．已知每辆60座客车的租费是45座客车租费的1.25倍，花4000元可租45座客车的辆数比租60座客车多2辆．
（1）问每辆45座客车租费和每辆60座客车租费分别是多少元？
（2）该校八年级师生共有400人，若只租用同一种客车，应该租用哪种客车合算？
25．（10分）如图，在平面直角坐标系xOy中，直线y＝ax+2a（a＞0）与x轴交于点A，与抛物线y＝ax2（a＞0）交于点B，C（点B在点C的左边）．
（1）求点A的坐标；
（2）作点B关于x轴的对称点B′，若以点A，B′，C为顶点的三角形为直角三角形，求a的值；
（3）我们把平面直角坐标系中横坐标与纵坐标均为整数的点叫作格点，如（0，2），（1，1）等均为格点．若直线y＝ax+2a（a＞0）与抛物线y＝ax2（a＞0）所围成的封闭图形内部（不包含边界）的格点数有且只有6个，请直接写出a的取值范围．
26．（12分）在矩形ABCD中，AB＝3，AD＝4，点E从点A出发，沿边AD，DC向点C运动，点A，D关于直线BE的对称点分别为点A′，D′，连接A′D′，BA′，ED′．
（1）【初步感知】如图1，当点D′落在BC的延长线上时，求DE的长；
（2）【深入探究】当点E运动到AD中点时，连接A′D，求A′D的长；
（3）【拓展运用】当直线A′D′恰好经过点C时，求DE的长．
2024年四川省成都市成华区中考数学二诊试卷
参考答案与试题解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）．
1．（4分）在π，﹣2，0，﹣1这四个实数中，最小的数是（ ）
A．πB．﹣2C．0D．﹣1
【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．
【解答】解：∵﹣2＜﹣1＜0＜π，
∴在π，﹣2，0，﹣1这四个实数中，最小的数是﹣2．
故选：B．
2．（4分）由一个长方体和一个圆柱组成的几何体如图所示，则这个几何体的俯视图是（ ）
A．B．
C．D．
【分析】根据从上面看得到的图形是俯视图即可解答．
【解答】解：从上面看下边是一个矩形，矩形的内部是一个圆．
故选：D．
3．（4分）经国家统计局初步核算，2023年我国国内生产总值1260582亿元，按不变价格计算，比上年增长5.2%．其中数据“1260582亿”用科学记数法表示为（ ）
A．1260582×108B．1.260582×1013
C．1.260582×1014D．1.260582×1015
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解；1260582亿＝126058200000000＝1.21×1014．
故选：C．
4．（4分）下列运算中，计算正确的是（ ）
A．（a2b）3＝a6b3B．5a﹣3a＝2
C．（a+b）2＝a2+b2D．a6÷a3＝a2
【分析】分别根据完全平方公式、合并同类项、幂的乘方与积的乘方、同底数幂的除法运算法则计算即可．
【解答】解：A、（a2b）3＝a6b3，符合题意；
B、5a﹣3a＝2a，不合题意；
C、（a+b）2＝a2+2ab+b2，不合题意；
D、a6÷a3＝a3，不合题意；
故选：A．
5．（4分）为了解学生参加体育锻炼的情况，从该班学生中随机抽取5名同学进行调查．经统计，他们的体育锻炼时间（单位：分钟）分别为：65，60，75，60，80．则这组数据的众数是（ ）
A．60B．65C．75D．80
【分析】根据众数的定义即可得出结论．
【解答】解：∵从该班学生中随机抽取5名同学进行调查，他们的体育锻炼时间（单位：分钟）分别为：65，60，75，60，80，其中60出现的次数最多，
∴这组数据的众数是60，
故选：A．
6．（4分）如图，直线m∥n，△ABC是等边三角形，顶点B在直线n上，直线m交AB于点E，交AC于点F，若∠1＝140°，则∠2的度数是（ ）
A．110°B．105°C．100°D．95°
【分析】根据等边三角形性质得∠A＝60°，再根据三角形外角定理得∠AEF＝∠1﹣∠A＝80°，则∠DEB＝∠AEF＝80°，然后根据平行线的性质得∠DEB+∠2＝180°，据此可得∠2的度数．
【解答】解：如下图所示：
∵△ABC为等边三角形，
∴∠A＝60°，
∵∠1是△AEF的一个外角，∠1＝140°，
∴∠1＝∠A+∠AEF，
∴∠AEF＝∠1﹣∠A＝140°﹣∠A＝140°﹣60°＝80°，
∴∠DEB＝∠AEF＝80°，
∵直线m∥n，
∴∠DEB+∠2＝180°，
∴∠2＝180°﹣∠DEB＝180°﹣80°＝100°．
故选：C．
7．（4分）如图，△ABC内接于⊙O，CD是⊙O的直径，若∠DCA＝38°，则∠ABC＝（ ）
A．56°B．52°C．48°D．38°
【分析】连接AD，由CD是⊙O的直径，∠DCA＝38°，得∠DAC＝90°，∠ADC＝52°，得∠ABC＝∠ADC＝52°．
【解答】解：连接AD，由CD是⊙O的直径，∠DCA＝38°，
得∠DAC＝90°，∠ADC＝52°，
得∠ABC＝∠ADC＝52°，
故选：B．
8．（4分）如图，二次函数y＝ax2+bx（a＜0）的图象过点A（2，0），下列结论错误的是（ ）
A．b＞0
B．a+b＞0
C．x＝2是关于x的方程ax2+bx＝0（a＜0）的一个根
D．若点（x1，y1），（x2，y2）在二次函数的图象上，且x1＞x2＞2，则y2＜y1＜0
【分析】依据题意，由抛物线开口向下，可得a＜0，又抛物线过（2，0），（0，0），从而可得抛物线的对称轴是直线x＝＝1＝﹣，故b＝﹣2a＞0，故可判断A；又a+b＝a﹣2a＝﹣a＞0，故可判断B；又二次函数y＝ax2+bx（a＜0）的图象过点A（2，0），则x＝2是关于x的方程ax2+bx＝0（a＜0）的一个根，故可判断C；又对称轴是直线x＝1，且开口向下，从而当x＞1时，y随x的增大而减小，再结合点（x1，y1），（x2，y2），（2，0）在二次函数的图象上，且x1＞x2＞2时，则y1＜y2＜0，故可判断D．
【解答】解：由题意，∵抛物线开口向下，
∴a＜0．
又抛物线过（2，0），（0，0），
∴抛物线的对称轴是直线x＝＝1＝﹣．
∴b＝﹣2a＞0，故A正确，不合题意．
∴a+b＝a﹣2a＝﹣a＞0，故B正确，不合题意．
∵二次函数y＝ax2+bx（a＜0）的图象过点A（2，0），
∴x＝2是关于x的方程ax2+bx＝0（a＜0）的一个根，故C正确，不合题意．
∵对称轴是直线x＝1，且开口向下，
∴当x＞1时，y随x的增大而减小．
∴当点（x1，y1），（x2，y2），（2，0）在二次函数的图象上，且x1＞x2＞2时，y1＜y2＜0，故D错误，符合题意．
故选：D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9．（4分）分解因式：ab2﹣2ab+a＝ a（b﹣1）2 ．
【分析】先提取公因式a，再对余下的多项式利用完全平方公式继续分解．
【解答】解：ab2﹣2ab+a，
＝a（b2﹣2b+1），
＝a（b﹣1）2．
故答案为：a（b﹣1）2．
10．（4分）如图，以正五边形ABCDE的顶点C为旋转中心，按顺时针方向旋转，使得新五边形A′B′CD′E′的顶点D′落在BC 的延长线上，则正五边ABCDE旋转的最小度数为 72° ．
【分析】根据旋转的性质，正多边形和圆的性质以及正多边形外角的计算方法进行计算即可．
【解答】解：如图，正五边形ABCDE的外角∠DCM＝＝72°，
即将正五边形ABCDE的顶点C为旋转中心，按顺时针方向旋转，使得新五边形A′B′CD′E′的顶点D′落在BC 的延长线上，则正五边ABCDE旋转的最小度数为72°，
故答案为：72°．
11．（4分）若直线y＝x向上平移3个单位长度后经过点（2，m），则m的值为 5 ．
【分析】先根据平移规律求出直线y＝x向上平移3个单位的直线解析式，再把点（2，m）代入，即可求出m的值．
【解答】解：将直线y＝x向上平移3个单位，得到直线y＝x+3，
把点（2，m）代入，得m＝2+3＝5．
故答案为：5．
12．（4分）元朝朱世杰的《算学启蒙》一书记载：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之．”其题意为：“良马每天行240里，劣马每天行150里，劣马先行12天，良马要几天追上劣马？”答：良马追上劣马需要的天数是 20 ．
【分析】设良马x天追上劣马，根据良马追上劣马所走路程相同可得：240x＝150（x+12），即可解得良马20天追上劣马．
【解答】解：设良马x天追上劣马，
根据题意得：240x＝150（x+12），
解得x＝20，
答：良马20天追上劣马；
故答案为：20．
13．（4分）如图，在▱ABCD中，AB＝12，BC＝8，AC交BD于点O．以点B为圆心，适当长为半径作弧，分别交AB，BC于点E，F；再分别以点E，F为圆心，大于的长为半径作弧，两弧交于点G；作射线BG交CD于点P．若BP的中点为点M，则OM的长为 2 ．
【分析】由作图知，BG平分∠ABC，得到∠ABG＝∠CBG，根据平行线的性质得到∠CPB＝∠ABP，求得∠CPB＝∠CBP，得到CP＝BC＝8，根据三角形中位线定理即可得到结论．
【解答】解：由作图知，BG平分∠ABC，
∴∠ABG＝∠CBG，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD＝12，BO＝DO，
∴∠CPB＝∠ABP，
∴∠CPB＝∠CBP，
∴CP＝BC＝8，
∴PD＝CD﹣CP＝4，
∵BP的中点为点M，
∴BM＝PM，
∴OM是△BPD的中位线，
∴OM＝PD＝2，
故答案为：2．
三、解答题（本大题共5个小题，共48分）
14．（12分）（1）计算：|1﹣|﹣4sin30°+（）﹣1+（2024﹣π）0．
（2）解不等式组：．
【分析】（1）按照去绝对值、零指数幂、负整数指数幂、三角函数的性质运算即可；
（2）分别解出不等式①②的解集后再确定不等式组的解集即可．
【解答】解：（1）|1﹣|﹣4sin30°+（）﹣1+（2024﹣π）0．
＝﹣4×+2+1
＝﹣1﹣2+2+1
＝；
（2）解不等式①得：x，
解不等式②得：x，
∴不等式组的解集为：．
15．（8分）《义务教育课程方案》和《义务教育劳动课程标准（2022年版）》正式发布，劳动课正式成为中小学一门独立课程．为培养同学们爱劳动的习惯，某校开展了“做好一件家务”主题活动（家务类型为：洗衣、刷碗、做饭、拖地），要求人人参与.9.1班劳动委员将本班同学做家务的信息绘制成了如图两幅尚不完整的统计图，请根据统计图信息，回答下列问题：
（1）9.1班学生共有 50 人；扇形统计图中“洗衣”对应扇形的圆心角度数为 108° ；若该校共有初中学生1500人，则可估计出该校初中学生中参与“做饭”的人数约有 150 人；
（2）9.1班评选出了近期做家务表现优秀的一男三女共四名同学，准备从这四名同学中随机选取两名同学分享体会，请用画树状图或列表的方法求所选同学中有男生的概率．
【分析】（1）用条形统计图中“刷碗”的人数除以扇形统计图中“刷碗”的百分比可得9.1班的学生人数；用360°乘以“洗衣”的人数所占的百分比，即可得扇形统计图中“洗衣”对应扇形的圆心角度数；求出9.1班参与“做饭”的人数，根据用样本估计总体，用1500乘以“做饭”的人数所占的百分比，即可得出答案．
（2）列表可得出所有等可能的结果数以及所选同学中有男生的结果数，再利用概率公式可得出答案．
【解答】解：（1）9.1班学生共有20÷40%＝50（人）．
扇形统计图中“洗衣”对应扇形的圆心角度数为360°×＝108°．
9.1班参与“做饭”的人数为50﹣15﹣20﹣10＝5（人），
∴估计该校初中学生中参与“做饭”的人数约有1500×＝150（人）．
故答案为：50；108°；150．
（2）列表如下：
共有12种等可能的结果，其中所选同学中有男生的结果有：（男，女），（男，女），（男，女），（女，男），（女，男），（女，男），共6种，
∴所选同学中有男生的概率为＝．
16．（8分）图1是一款手机支架，由托板、支撑板和底座构成，图2是手机放置在托板上后侧面的截面图．量得托板BC长为40mm，支撑板CD长为80mm，手机AB长为120mm，∠DCB＝50°，∠CDE＝75°，求手机顶端A到底座DE的距离AH的长（结果精确到1mm）．参考数据：sin75°≈0.966，cs75°≈0.259，tan75°≈3.732，sin35°＝cs55°≈0.574，cs35°＝sin55°≈0.819，tan35°≈0.7，tan55°≈1.428．
【分析】通过作垂线，构造直角三角形，利用直角三角形的边角关系，求出FH、AF，即可求出点A到直线DE的距离．
【解答】解：如图，过点C作CF⊥AH，垂足为F，过点C作CN⊥DE，垂足为N，
由题意可知，AC＝80mm，CD＝80mm，∠DCB＝50°，∠CDE＝75°，
在Rt△CDN中，
CN＝CD•sin∠CDE＝80×sin75°＝80×0.966≈77（mm），
∴FH＝CN＝77mm，
∵CF∥DN，
∴∠CDN＝∠DCF＝75°，
∴∠ACF＝180°﹣∠DCF﹣∠BCD＝55°，
在Rt△AFC中，
AF＝AC•sin55°＝80×0.819≈66（mm），
AH＝AF+FH＝77+66＝143（mm），
答：点A到直线DE的距离约为143mm．
17．（10分）如图，AB为⊙O的直径，C是下半圆弧的中点，D为半径OA（除端点外）上一点，CD的延长线交⊙O于点E，过点E作⊙O的切线交BA的延长线于点F．
（1）求证：FD＝FE；
（2）若BD＝7，，求⊙O的半径及tanF的值．
【分析】（1）连接OE、OC，如图，根据垂径定理得到OC⊥AB，根据切线的性质得到∠OEF＝90°，然后证明∠FED＝∠FDE得到FD＝FE；
（2）设⊙O的半径为r，则OC＝r，OD＝BD﹣OB＝7﹣r，先在Rt△OCD中利用勾股定理得到（7﹣r）2+r2＝（）2，解方程得到OD＝2，OE＝5，设FE＝FD＝x，则OF＝x+2，接着在RtOEF中利用勾股定理得到x2+52＝（x+2）2，解方程得x＝，然后根据正切的定义求解．
【解答】（1）证明：连接OE、OC，如图，
∵C是下半圆弧的中点，
∴OC⊥AB，
∴∠COA＝90°，
∵EF为⊙O的切线，
∴OE⊥EF，
∴∠OEF＝90°，
∵OE＝OC，
∴∠OEC＝∠OCE，
∵∠OEC+∠FED＝90°，∠OCE+∠ODC＝90°，
∴∠FED＝∠ODC，
∵∠ODC＝∠FDE，
∴∠FED＝∠FDE，
∴FD＝FE；
（2）解：设⊙O的半径为r，则OC＝r，OD＝BD﹣OB＝7﹣r，
在Rt△OCD中，（7﹣r）2+r2＝（）2，
解得r1＝2（舍去），r2＝5，
∴OD＝2，OE＝5，
设FE＝FD＝x，则OF＝x+2，
在RtOEF中，x2+52＝（x+2）2，
解得x＝，
即FE＝，
∴tanF＝＝＝．
18．（10分）如图，一次函数y＝x+2的图象与反比例函数y＝（x＞0）的图象交于点A（a，3），与y轴交于点B．
（1）求反比例函数的解析式；
（2）若C为反比例函数y＝（x＞0）图象上一点，直线AC与x轴交于点D，且满足AD＝2AC，求点C的坐标．
（3）若点P在反比例函数y＝（x＞0）图象上，点Q在x轴上，且以点A，B，P，Q为顶点的四边形是平行四边形，请直接写出符合条件的点P的坐标．
【分析】（1）先求出a值，再用待定系数法求出反比例函数解析式即可；
（2）分两种情况进行解答，①如图1当点C在A点下方时，②如图2当C在A点上方时解出点C坐标即可；
（3）分两种情况进行解答，①当AB为平行四边形的边时，ABQ′P′是平行四边形，②当AB为平行四边形的对角线时，ABQP是平行四边形，分别求出点P坐标即可．
【解答】解：（1）∵点A（a，3）在直线y＝x+2的图象上，
∴，解得a＝2，
∴A（2，3），
∵A（2，3）在反比例函数y＝（x＞0）的图象上，
∴k＝2×3＝6，
∴反比例函数的解析式为：y＝；
（2）分两种情况，①如图1，当点C在A点下方时，
∵AD＝2AC，A（2，3），
∴点C为AD中点，
∴点C纵坐标为，
当y＝时，x＝6×＝4，
∴C（4，），
②如图2，当C在A点上方时，
∵AD＝2AC，A（2，3），
∴，即，解得yC＝，
将yC代入反比例函数解析式得：x＝，
∴C（，）．
综上分析，点C坐标为（4，）或（，）．
（3）∵直线AB解析式为y＝x+2，
∴B（0，2），A（2，3），分两种情况讨论：
如图3：
①当AB为平行四边形的边时，ABQ′P′是平行四边形，
yQ′﹣yB＝yP′﹣yA，即0﹣2＝yP′﹣3，解得yP′＝1，
∴P′（6，1），
②当AB为平行四边形的对角线时，APBQ是平行四边形，
∵B（0，2），A（2，3），又Q点纵坐标为0，
∴yP＝2+3﹣0＝5，
当y＝5时，x＝，
∴P（，5）．
综上分析，P（，5）或P（，5）．
一、填空题（本大题共5个小题，每小题4分，共20分）
19．（4分）若m、n满足3m﹣n﹣4＝0，则8m÷2n＝ 16 ．
【分析】直接利用幂的乘方运算法则将原式变形，进而计算得出答案．
【解答】解：∵3m﹣n﹣4＝0，
∴3m﹣n＝4，
∴8m÷2n＝23m÷2n＝23m﹣n＝24＝16．
故答案为：16．
20．（4分）《墨子•天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，以面积为4的正方形ABCD的中心O为位似中心，作它的位似图形A′B′C′D′，若A′B′：AB＝2：1，则四边形A′B′CD′的外接圆的面积为 8π ．
【分析】如图，连接B′D′．利用相似多边形的性质求出正方形A′B′C′D′的面积，求出边长，再求出B′D′可得结论．
【解答】解：如图，连接B′D′．设B′D′的中点为O．
∵正方形ABCD∽正方形A′B′C′D′，相似比为1：2，
又∵正方形ABCD的面积为4，
∴正方形A′B′C′D′的面积为16，
∴A′B′＝A′D′＝4，
∵∠B′A′D′＝90°，
∴B′D′＝A′B′＝4，
∴正方形A′B′C′D′的外接圆的面积＝8π，
故答案为：8π．
21．（4分）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点P为BC边上一动点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长的最小值为 ．
【分析】设AC与PQ交于点O，过点O作OD⊥BC于点D，先求出AC＝4，根据平行四边形性质得PQ＝2OP，OC＝AC＝2，证△ODC∽△BAC相似得OD＝，然后根据PQ＝2OP得当OP为最小时，PQ为最小，根据“垂线段最短”得OP≥OD＝，由此可得OP的最小值，进而可得PQ的最小值．
【解答】解：设AC与PQ交于点O，过点O作OD⊥BC于点D，如下图所示：
在Rt△ABC中，AB＝3，BC＝5，
由勾股定理得：AC＝＝4，
∵四边形PAQC为平行四边形，
∴点O为AC，PQ的中点，
∴PQ＝2OP，OC＝AC＝2，
∵OD⊥BC，∠BAC＝90°，
∴∠ODC＝∠BAC＝90°，∠OCD＝∠BCA，
∴△ODC∽△BAC，
∴OD：AB＝OC：BC，
即OD：3＝2：5，
∴OD＝，
∵PQ＝2OP，
∴当OP为最小时，PQ为最小，
根据“垂线段最短”得：OP≥OD，
即OP≥，
∴OP的最小值为，
∴PQ的最小值为．
故答案为：．
22．（4分）数学综合与实践活动小组用四个全等的直角三角形（Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA）拼成如图所示的“赵爽弦图”，得到正方形ABCD和正方形EFGH，连接AC和EG，AC与DF，EG，BH分别相交于点P，O，Q．若，则的值是 ．
【分析】设EC＝x（x＞0），EQ＝15a（a＞0），则BE＝14a，证明△AHQ∽△CEQ，利用相似三角形的性质求出EC＝BH＝35a，可得QH＝6a，EH＝21a，利用勾股定理求出BC和AQ，进而可得OQ的长，再证明△QEO≌△PGO，可得OP＝OQ＝a，然后根据正方形的性质求出OE，即可得出答案．
【解答】解：设EC＝x（x＞0），BE＝14a（a＞0），则QE＝15a，
∵∠AHQ＝∠CEQ＝90°，∠AQH＝∠CQE，
∴△AHQ∽△CEQ，
∴＝，
∵Rt△AHB≌Rt△BEC，
∴AH＝BE＝14a，BH＝EC＝x，
∴QH＝BH﹣BE﹣EQ＝x﹣29a，
∴＝，
整理得：x2﹣29ax﹣210a2＝0，
解得：x1＝35a，x2＝﹣6a （不合题意，舍去），
即EC＝BH＝35a，
∴QH＝EH﹣EQ＝35a﹣29a＝6a，EH＝BH﹣BE＝35a﹣14a＝21a，
∴BC＝＝7a，AQ＝＝2a，
∴AC＝BC＝7a，
∴OA＝AC＝a，
∴OQ＝OA﹣AQ＝a，
∵四边形HEFG是正方形，
∴∠QEO＝∠PGO，OE＝OG，
又∵∠QOE＝∠POG，
∴△QEO≌△PGO（SAS），
∵OP＝OQ＝a，
又∵EG＝EH＝21，
∴OE＝EG＝，
∴＝＝，
故答案为：．
23．（4分）若点M（x，y）的坐标满足x2＝t﹣5y，y2＝t﹣5x，其中x≠y，t为常数，则称点M为“好点”．若双曲线 上存在“好点”，则k的取值范围是 ≤k＜ ．
【分析】根据题意列出方程组，解方程组得到（x﹣）（x+﹣5）＝0，依据条件得到x+＝0，整理出k的代数式按照自变量取值范围确定k的范围即可．
【解答】解：∵双曲线 上存在“好点”，
∴，
①﹣②得：（x﹣）（x+）＝5（x﹣），
∴（x﹣）（x+﹣5）＝0，
∵x≠y，
∴x+＝0，
整理得：k＝5x﹣x2＝﹣x2+5x＝﹣（x2﹣5x）＝﹣（x﹣）2+，
∵，
∴≤k＜．
故答案为：≤k＜．
二、解答题（本大题共3个小题，共30分）
24．（8分）某校为落实立德树人的根本任务，积极探索“五育并举，融合育人”的育人途径，计划组织八年级师生租用客车到成都大熊猫基地开展跨学科主题研学活动．已知每辆60座客车的租费是45座客车租费的1.25倍，花4000元可租45座客车的辆数比租60座客车多2辆．
（1）问每辆45座客车租费和每辆60座客车租费分别是多少元？
（2）该校八年级师生共有400人，若只租用同一种客车，应该租用哪种客车合算？
【分析】（1）设每辆45座客车租费是x元，则每辆60座客车租费是1.25x元，根据花4000元可租45座客车的辆数比租60座客车多2辆．列出分式方程，解方程即可；
（2）求出租用45座客车9辆的租费和租用60座客车7辆的租费，再比较即可．
【解答】解：（1）设每辆45座客车租费是x元，则每辆60座客车租费是1.25x元，
由题意得：﹣＝2，
解得：x＝400，
经检验，x＝400是原方程的解，且符合题意，
∴1.25x＝1.25×400＝500，
答：每辆45座客车租费是400元，每辆60座客车租费是500元；
（2）∵400÷45＝8，400÷60＝6，
∴租用45座客车9辆，租费为9×400＝3600（元），
租用60座客车7辆，租费为7×500＝3500（元），
∵3500＜3600，
∴租用60座客车合算．
25．（10分）如图，在平面直角坐标系xOy中，直线y＝ax+2a（a＞0）与x轴交于点A，与抛物线y＝ax2（a＞0）交于点B，C（点B在点C的左边）．
（1）求点A的坐标；
（2）作点B关于x轴的对称点B′，若以点A，B′，C为顶点的三角形为直角三角形，求a的值；
（3）我们把平面直角坐标系中横坐标与纵坐标均为整数的点叫作格点，如（0，2），（1，1）等均为格点．若直线y＝ax+2a（a＞0）与抛物线y＝ax2（a＞0）所围成的封闭图形内部（不包含边界）的格点数有且只有6个，请直接写出a的取值范围．
【分析】（1）当y＝0时，求A点坐标即可；
（2）分别求出B'、C坐标，可得AC2＝16+16a2，B'C2＝9+25a2，AB'2＝1+a2，再分三种情况，利用勾股定理建立方程求a的值即可；
（3）画出图象，结合图象，当直线y＝ax+2a经过点（0，3）时，a＝，此时有5个格点；当直线y＝ax+2a经过点（1，5）时，a＝，此时有6个格点；当a＝2时，此时有6个格点；即可求＜a≤或a＝2时，有6个格点．
【解答】解：（1）当y＝0时，x＝﹣2，
∴A（﹣2，0）；
（2）当ax+2a＝ax2时，解得x＝2或x＝﹣1，
∴B（﹣1，a），C（2，4a），
∵B'与B关于x轴对称，
∴B'（﹣1，﹣a），
∴AC2＝16+16a2，B'C2＝9+25a2，AB'2＝1+a2，
①当AC为斜边时，16+16a2＝9+25a2+1+a2，
解得a＝或a＝﹣（舍）；
②当B'C为斜边时，9+25a2＝16+16a2+1+a2，
解得a＝1或a＝﹣1（舍）；
③当AB'为斜边时，1+a2＝16+16a2+9+25a2，
此时a无解；
综上所述：a的值为或1；
（3）如图：当直线y＝ax+2a经过点（0，3）时，a＝，此时有5个格点；
当直线y＝ax+2a经过点（1，5）时，a＝，此时有6个格点；
当a＝2时，此时有6个格点；
综上所述：＜a≤或a＝2时，有6个格点．
26．（12分）在矩形ABCD中，AB＝3，AD＝4，点E从点A出发，沿边AD，DC向点C运动，点A，D关于直线BE的对称点分别为点A′，D′，连接A′D′，BA′，ED′．
（1）【初步感知】如图1，当点D′落在BC的延长线上时，求DE的长；
（2）【深入探究】当点E运动到AD中点时，连接A′D，求A′D的长；
（3）【拓展运用】当直线A′D′恰好经过点C时，求DE的长．
【分析】（1）连接BD，设DE＝x，则EC＝3﹣x，由对称性得ED'＝ED＝x，由勾股定理求出BD＝5，列出方程（3﹣x）2+12＝x2，可得出答案；
（2）连接AA'，交BE于点F，由对称性得AA'⊥BE，证明△AEF∽△BEA，得出，求出EF的长，由三角形中位线定理可得出答案；
（3）分两种情况，由矩形的性质，相似三角形的性质及勾股定理可得出答案．
【解答】解：（1）如图1，连接BD，
设DE＝x，则EC＝3﹣x，由对称性得ED'＝ED＝x，
∵四边形ABCD是矩形，
∴AB＝DC＝3，AD＝BC＝4，∠A＝90°，
∴在Rt△BAD中，，
由对称性得BD'＝BD＝5，
∴CD'＝5﹣4＝1，
在△ECD'中，EC2+CD'2＝ED'2，
∴（3﹣x）2+12＝x2，
解得，
即，
（2）如图1，连接AA'，交BE于点F，由对称性得AA'⊥BE，
∵点E是AD中点，
∴AE＝DE＝2，
在Rt△ABE中，，
在△ABE中，∠EAB＝90°，AF⊥BE，
∴∠AEF＝∠AEB，∠AFE＝∠EAB，
∴△AEF∽△BEA，
∴，
∴，
由对称性得A′E＝AE，
∴A′E＝AE＝DE，
∴∠AA'D＝90°，
∴AA′⊥A′D，
∴A′D∥FE，
∵点E是AD的中点，
∴点F是AA′的中点，
∴FE是△AA'D 的中位线，
∴；
（3）分以下两种情况讨论：
①如图，当点E在边AD上时，A'D'恰好经过点C，
∴由对称性得∠1＝∠A＝90°，BA'＝BA＝CD＝3，
∴∠2＝∠1＝90°，
∴在Rt△BCA′中，，
∵在矩形ABCD中，AD∥BC，∠D＝90°，
∴∠3＝∠4，∠2＝∠D，
在△BCA′和△CED中，
，
∴△BCA′≌△CED（AAS），
∴；
②如图3，当点E在边CD上时，A′D恰好经过点C，
∴由对称性得∠A'＝∠A＝90°，∠D'＝∠D＝90°，BA'＝BA＝3，A'D'＝AD＝4，
∴∠A'＝∠D'＝90°，
在Rt△BCA′中，，
∴，
∵A'D'恰好经过点C，
∴∠5+∠6+∠BCD＝180°，
∵在矩形ABCD中，∠BCD＝90°，
∴∠5+∠6＝90°，
∵∠A'＝90°，
∴∠7+∠6＝90°，
∴∠5＝∠7，
在△ECD'和△CBA′中，∠D'＝∠A'，∠5＝∠7，
∴△ECD'∽△CBA'，
∴，
∴，
解得，
即，
综上所述，DE的长为或．
男
女
女
女
男
（男，女）
（男，女）
（男，女）
女
（女，男）
（女，女）
（女，女）
女
（女，男）
（女，女）
（女，女）
女
（女，男）
（女，女）
（女，女）