2024届高考数学学业水平测试复习专题五第21讲平面向量的应用课件

这是一份2024届高考数学学业水平测试复习专题五第21讲平面向量的应用课件，共34页。PPT课件主要包含了续上表，2如图所示，解析如图所示等内容，欢迎下载使用。
第21讲　平面向量的应用1．向量在平面几何中的应用(1)用向量解决常见平面几何问题的技巧：
2．平面向量在物理中的应用(1)由于物理学中的力、速度、位移都是矢量，它们的分解与合成与向量的加法和减法相似，可以用向量的知识来解决．(2)物理学中的功是一个标量，是力F与位移s的数量积，即W＝F·s＝|F||s|cs θ(θ为F与s的夹角)．3．余弦定理(1)三角形中任何一边的平方，等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍，即：a2＝b2＋c2－2bccs A；b2＝c2＋a2－2cacs B；c2＝a2＋b2－2abcs C.
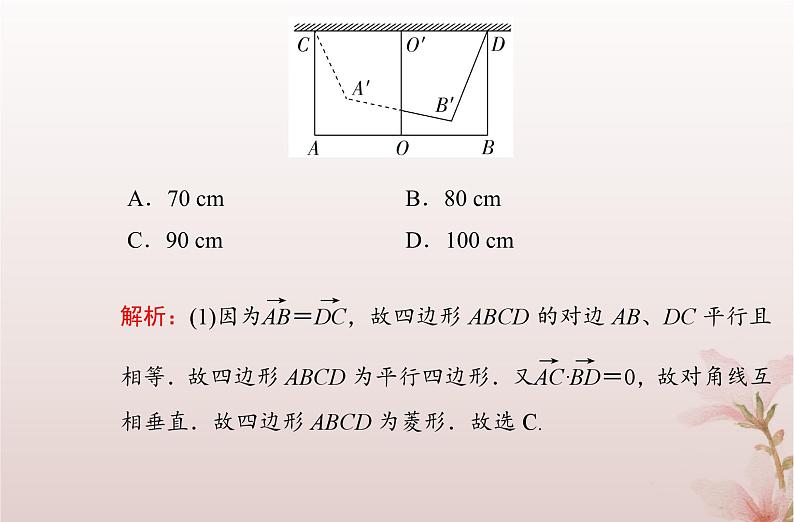
(2)如图，教室里悬挂着日光灯管AB，AB＝120 cm，灯线AC＝BD，将灯管AB绕着过AB中点O的铅垂线OO′顺时针旋转60°至A′B′，且始终保持灯线绷紧，若旋转后该灯管升高了20 cm，则AC的长为(　　)
A．70 cm B．80 cmC．90 cm D．100 cm
(2)设A′B′与OO′交于点N，过点A′作A′M⊥AC于M，连接MN，如图所示．
答案：(1)C　(2)D
剖析：向量法解决平面几何问题的“三步曲”
2．向量的在物理中的应用 (1)河水的流速为5 m/s，一艘小船想沿垂直于河岸方向以12 m/s的速度驶向对岸，则小船的静水速度大小为(　　)A．13 m/s B．12 m/sC．17 m/s D．15 m/s
解析：(1)设河水的流速v2＝5 m/s，静水速度与河水速度的合速度v＝12 m/s，小船的静水速度为v1，为了使航向垂直河岸，船头必须斜向上游方向，即静水速度v1斜向上游方向，河水速度v2＝5 m/s平行于河岸，静水速度与河水速度的合速度v＝12 m/s指向对岸，
答案：(1)A　(2)A剖析：(1)物理问题中常见的向量有力、速度、位移等．(2)向量的加减法运算体现在一些物理量的合成和分解中．(3)动量mv是向量的数乘运算．(4)功是力F与位移s的数量积．
3．正余弦定理在解三角形中的应用 (1)(2023·广东模拟)在△ABC中，内角A，B，C所对的边分别为a，b，c，且b2＋c2＝a2＋bc.若sin B·sin C＝sin2 A，则△ABC的形状是(　　)A．钝角三角形 B．直角三角形C．等边三角形 D．等腰直角三角形
答案：(1)C　(2)B剖析：已知三角形的两边和其中一边的对角解三角形可用正弦定理，也可用余弦定理．用正弦定理时需判断其解的个数，用余弦定理时可根据一元二次方程根的情况判断解的个数．
4．正余弦定理的实际应用 (1)王之涣《登鹳雀楼》：白日依山尽，黄河入海流，欲穷千里目，更上一层楼．诗句不仅刻画了祖国的壮丽河山，而且揭示了“只有站得高，才能看得远”的哲理，因此成为千古名句．我们从数学角度来思考：欲穷千里目，需上几层楼？把地球看作球体，地球半径R＝6 371 km，如图，设O为地球球心，人的初始位置为点M，点N是人登高后的位置(人的高度忽略不计)，按每层楼高3 m计算，“欲穷千里目”即弧AM的长度为500 km，则需要登上楼的层数约为(　　)
(2)如图，一辆汽车在一条水平的公路上向正西方向行驶，到A处时测得公路北侧一山顶D在西偏北45°的方向上，行驶600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为60°，则此山的高度CD为(　　)
答案：(1)C　(2)C
1．已知△ABC的三个顶点的坐标分别为A(3，4)，B(5，2)，C(－1，－4)，则该三角形为(　　)A．锐角三角形　　　　B．直角三角形C．钝角三角形 D．等腰直角三角形
5．如图，海平面上的甲船位于中心O的南偏西30°，与O相距15 nmile的C处．现甲船以35 nmile/h的速度沿直线CB去营救位于中心O正东方向25 nmile的B处的乙船，则甲船到达B处需要的时间为__________h.
△OBC中，∠BOC＝30°＋90°＝120°，OC＝15，OB＝25；所以BC2＝152＋252－2×15×25×cs 120°＝1 225，即BC＝35，又甲船的速度为35 nmile/h，所以甲船到达B处需要的时间为35÷35＝1(h)．故答案为1.答案：1