中考数学复习课件——-二次函数存在性问题

这是一份中考数学复习课件——-二次函数存在性问题，共32页。PPT课件主要包含了CONTENTS，考点1，考点2，考点3，考点4，题目分析等内容，欢迎下载使用。

二次函数与相似三角形问题
二次函数与直角三角形问题
二次函数与等腰三角形问题
二次函数与平行四边形问题（含特殊四边形）
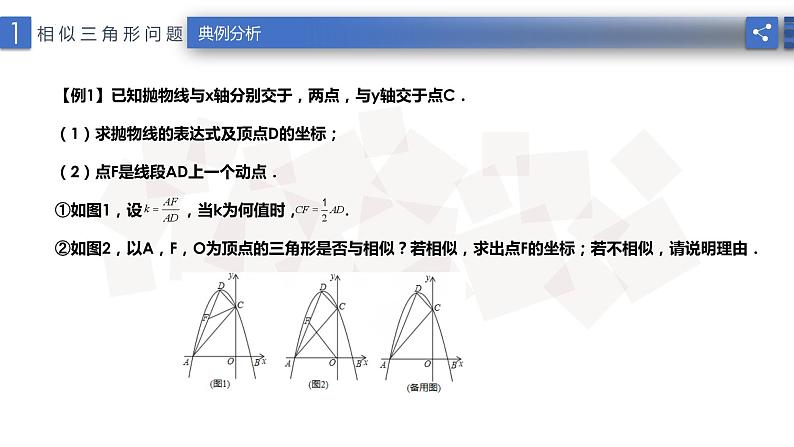
【例1】已知抛物线与x轴分别交于，两点，与y轴交于点C．（1）求抛物线的表达式及顶点D的坐标；（2）点F是线段AD上一个动点． ①如图1，设 ，当k为何值时， .②如图2，以A，F，O为顶点的三角形是否与相似？若相似，求出点F的坐标；若不相似，请说明理由．
【例1】已知抛物线与x轴分别交于，两点，与y轴交于点C．（1）求抛物线的表达式及顶点D的坐标；
【例1】已知抛物线与x轴分别交于，两点，与y轴交于点C．（2）点F是线段AD上一个动点． ①如图1，设 ，当k为何值时， .
【例1】已知抛物线与x轴分别交于，两点，与y轴交于点C．（2）②如图2，以A，F，O为顶点的三角形是否与相似？若相似，求出点F的坐标；若不相似，请说明理由．
本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、相似三角形的判定与性质和直角三角形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．
（1）将A、C的坐标代入 求出a、c即可得到解析式；（2）先求出E点坐标，然后作AE的垂直平分线，与x轴交于Q，与y轴交于Q'，根据垂直平分线的性质可知Q、与A、E，Q'与A、E组成的三角形是以AE为底边的等腰三角形，设Q点坐标(0,x)，Q'坐标(0,y)，根据距离公式建立方程求解即可；（3）根据A、E坐标，求出AE长度，然后推出∠BAE=∠ABC=45°，设 ，由相似得到 或 ，建立方程求解即可．
【例3】如图，已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（1）求抛物线的表达式；（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；（3）若抛物线上有一动点M，使△ABM的面积等于△ABC的面积，求M点坐标．（4）抛物线的对称轴上是否存在动点Q，使得△BCQ为等腰三角形？若存在，求出点Q的坐标；若不存在，说明理由．
【例3】如图，已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（1）求抛物线的表达式；
【例3】如图，已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；
【例3】如图，已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（3）若抛物线上有一动点M，使△ABM的面积等于△ABC的面积，求M点坐标．
【例3】如图，已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（4）抛物线的对称轴上是否存在动点Q，使得△BCQ为等腰三角形？若存在，求出点Q的坐标；若不存在，说明理由．
【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、二次函数的性质、两点间的距离公式、三角形的面积、等腰三角形的性质以及解一元二次（或一元一次）方程，解题的关键是：（1）由点的坐标，利用待定系数法求出二次函数表达式；（2）利用两点之间线段最短，找出点P的位置；（3）利用两三角形面积相等，找出关于x的一元二次方程；（4）分BQ=BC，CQ=CB及QB=QC三种情况，找出关于m的方程．
（1）把点A、B的坐标代入函数解析式，解方程组求出a、b的值，即可得解；（2）根据抛物线解析式求出对称轴，再根据平行四边形的对角线互相平分求出点C的横坐标，然后代入函数解析式计算求出纵坐标，即可得解；（3）设AC、EF的交点为D，根据点C的坐标写出点D的坐标，然后分①O是顶角，②C是顶角，③P是顶角三种情况讨论．
（1）把A（0，﹣4）代入可求c，运用根与系数的关系及 ，可求出b；（2）因为菱形的对角线互相垂直平分，故菱形的另外一条对角线必在抛物线的对称轴上，满足条件的D点，就是抛物线的顶点；（3）由四边形BPOH是以OB为对角线的菱形，可得PH垂直平分OB，求出OB的中点坐标，代入抛物线解析式即可，再根据所求点的坐标与线段OB的长度关系，判断是否为正方形即可．