






中考数学专项复习课件 《二次函数存在性问题解析》
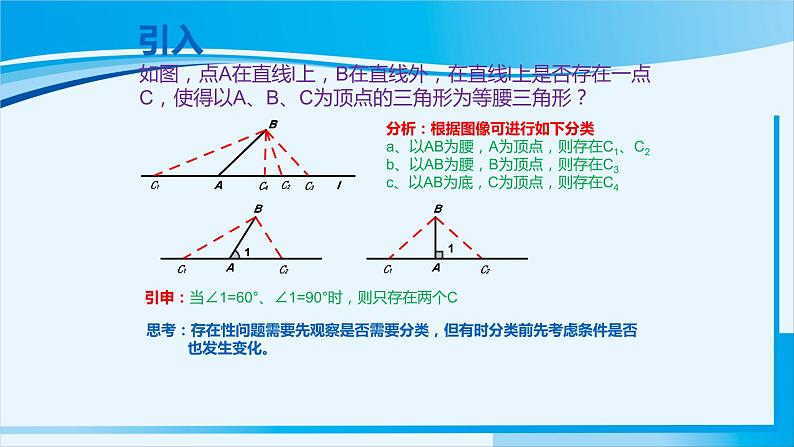
展开如图,点A在直线l上,B在直线外,在直线l上是否存在一点C,使得以A、B、C为顶点的三角形为等腰三角形?
分析:根据图像可进行如下分类a、以AB为腰,A为顶点,则存在C1、C2b、以AB为腰,B为顶点,则存在C3c、以AB为底,C为顶点,则存在C4
引申:当∠1=60°、∠1=90°时,则只存在两个C
思考:存在性问题需要先观察是否需要分类,但有时分类前先考虑条件是否 也发生变化。
特殊三角形存在性问题选题:等腰三角形存在性问题直角三角形存在性问题知识回顾:特殊三角形的判定等腰三角形的判定:两底脚相等、两腰长相等等边三角形的判定:两角60°、三边相等、含60°的等腰直角三角形的判定:一个角为90°、勾股定理等腰直角三角形的判定:有一个角为45°的直角三角形、两直角边相等的直角三角形。坐标系内知识点点点距公式:
例1、如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已BC//x知轴,点A在x轴上,点C在y轴上,且AC=BC.(1)求抛物线的对称轴;(解: )(2)写出A、B、C三点的坐标并求抛物线的解析式;(解:A(-3,0),B(5,4),C(0,4), )(3)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在△PAB是等腰三角形.若存在,求出所有符合条件的点P坐标;不存在,请说明理由.
思路点拨:1、不确定的点:点P 2、点P在对称轴上,且在x轴下方 3、分类:a)AB为腰,A为顶点,关系式:PA=AB b)AB为腰,B为顶点,关系式:PB=BA c)AB为底,P为顶点,关系式:PA=PB 4、根据分类依次列式计算,可设P点坐标为(2.5,y) 5、验算符合条件的P点坐标简要过程如下:A(-3,0),B(5,4),P(2.5,y)根据分类的三种情况分别算出:a) b) c)综上:(略)
例2、在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.(1)求点B的坐标;(解:B(-3,1))(2)求抛物线的解析式;(解: )(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
思路点拨:1、不确定的点:点P 2、点P在抛物线上 3、分类:a)AC⊥CP,P为直线CP与抛物线交点 b)AC⊥AP,P为直线AP与抛物线交点 4、求直线方程,联立抛物线求交点 5、求完交点,验算是否为等腰简要过程如下:a)CP直线方程就是BC: 联立抛物线方程得: 解得: ,则P(1,-1),可验的此P点满足题意。b)AP直线方程为: 联立抛物线方程得: 解得: ,则P1(2,1),P2(-4,6),可验的此P1点满足题意,P2不满足,舍去。 综上:(略)
相似三角形存在性问题选题:存在相等的角的相似存在性问题构造相等的角的相似存在性问题知识回顾:相似三角形的判定1、平行出相似2、三组对应边成比例3、两组对应边成比例,且夹角相等4、两组对应角相等坐标系内知识点点点距公式:
存在相等的角的相似存在性问题
例3、如图,已知抛物线y=ax2+bx+3与y轴交于点A,且经过B(1,0)、C(5,8)两点,点D是抛物线顶点,E是对称轴与直线AC的交点,F与E关于点D对称.(1)求抛物线的解析式;(解: y=x2-4x+3 )(2)求证:∠AFE=∠CFE;(解:D(2,-1),E(2,5),F(2,-7),tan∠AFE=0.2=tan∠CFE)(3)在抛物线的对称轴上是否存在点P,使△AFP与△FDC相似.若有,请求出所有符合条件的点P的坐标;若没有,请说明理由.
思路点拨:1、确定的三角形:△FDC,不确定的点P 2、P点在对称轴上 3、两个三角形存在相等的角:∠AFP=∠CFD 4、根据相似三角形相等的角的两边成比例分类: a)AF:FC=FP:FD b)AF:FD=PF:FC 5、设P的坐标为(2,y),根据分类的情况列方程求简要过程如下:a)解得y=-3,即P(2,-3)b)解得y=19,即P(2,19)综上:(略)
构造相等的角的相似存在性问题
例4、在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.(1)求抛物线解析是及顶点C的坐标.(解:y=-x2-2x+3,C(-1,4))(2)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
思路点拨:1、确定的三角形:△ACH,不确定的△PCQ 2、P点在抛物线上 3、两个都是直角三角形,可考虑构造另一个角相等来构造相似, 分类:a)∠ACP=∠CAH构造 b)∠ACP=∠ACH构造 4、画出辅助线,求出CP所在直线方程,求直线与抛物线的交点简要过程如下:a)∠ACP=∠CAH时,△ACD为等腰设D(d,0),利用AD=CD求的D(2,0) 直线CD为: ,联立抛物线: ,解得:b)∠ACP=∠ACH,AC为∠ECH的平分线,作AM⊥CE于M点,则AM=AH,设E(e,0),由△AEM∽△CEH知: AM:CH=AE:EC,其中: 可求得 ,直线CE为:综上:(略)
四边形存在性问题选题:平行四边形存在性问题菱形存在性问题直角梯形存在性问题知识回顾:特殊四边形的判定平行四边形的判定:1、两组对边平行。2、两组对边相等。3、两组对角相等。4、对角线互相平分。 5、一组对边平行且相等矩形的判定:1、有一个角为直角的□。2、三个角为直角的四边形。3、对角线相等的□菱形的判定:1、有一组邻边相等□。2、四条边相等四边形。3、对角线互相垂直的□正方形的判定:1、是菱形的矩形。2、是矩形的菱形梯形的判定:一组对边平行,另一组对边不平行直角梯形的判定:有一角为直角的梯形等腰梯形的判定:1、两腰长相等的梯形。2、两底角相等的梯形坐标系内知识点点点距公式: 线段中点坐标:
例5、如图,已知抛物线y=ax2-2ax-3与x轴交于A、B两点,其顶点为C,过点A的直线交抛物线于另一点D(2,-3),且tan∠BAD=1.(1)求抛物线的解析式;(解:y=x2-2x-3 )(2)点Q是抛物线上的动点,在x轴上是否存在点F,使以A,D,F,Q为顶点的四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
思路点拨:1、确定的点:A(-1,0),D(2,-3).不确定的点F,Q 2、F点在x轴上,Q点在抛物线上,可设F(m,0),Q(x,y),y=x 2-2x-3 3、利用对角线互相平分判定四边形是平行四边形,可分类为三种情况: a)AD,FQ为对角线 b)AF,DQ为对角线 c)AQ,DF为对角线 4、利用对角线互相平分即对角线中点坐标为同一点列出方程, 找出四点坐标关系,直至最后求出未知点的坐标。简要过程如下:a)AD,FQ为对角线: -1+2=m+x 0-3=0+y 解得:y=-3,m=-x+1,代入y=x2-2x-3解得x1=0,x2=2(舍) ∴m=1,则F(1,0)b)AF,DQ为对角线: -1+m=2+x 0+0=-3+y 解得:y=3,m=x+3,代入y=x2-2x-3解得: ∴ c)AQ,DF为对角线 -1+x=2+m 0+y=-3+0 解得:y=-3,m=x-3,代入y=x2-2x-3解得x1=0,x2=2(舍) ∴m=-3,则F(-3,0)综上:(略)
例6、如图,抛物线 与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).(1)求直线AB的函数关系式;(解:A(0,1),B(3,2.5), )(2)动点P在线段OC上,从原点O出发以每钞一个单位的速度向C移动,过点P作⊥x轴,交直线AB于点M,抛物线于点N,设点P移动的时间为t秒,MN的长为s个单位,求s与t的函数关系式,并写出t的取值范围;(解: )(3)设(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t的值,平行四边形BCMN是否为菱形?说明理由.
思路点拨:1、确定的关系:MN//BC 2、加上条件MN=BC,利用一边平行且相等判定平行四边形 3、在平行四边形基础上再去判断是否为菱形简要过程如下: 利用BC=MN求得:t1=1,t2=2当t=1时, ,MC=BC,四边形BCMN为菱形。当t=2时, ,MC≠BC,四边形BCMN不是菱形。综上:(略)
例7、如图,二次函数y=-x2+ax+b的图像与x轴交于A(- ,0)、 B(2,0)两点,且与y轴交于点C; (1) 求该拋物线的解析式,并判断△ABC的形状;(解: ,△ABC为直角三角形 ) (2) 在x轴上方的拋物线上有一点D,且以A、C、D、B四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;(解: ) (3) 在此拋物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。
思路点拨:1、确定的位置关系:AC⊥BC,不确定的点P点 2、P点在抛物线上 3、利用AC⊥BC知AC,BC中必有一条是底,一条是腰分类 a)BC为底,则AP也为底,AP//BC b)AC为底,则BP也为底,BP//AC 4、按照上面的分类分别求出AP,BP的直线关系式 5、直线关系式联立抛物线关系式求出交点坐标即为P点简要过程如下:a)BC为底,则AP也为底,AP//BC,BC: 代入A点可求出AP:b)AC为底,则BP也为底,BP//AC,AC: 代入B点可求出BP:综上:(略)
(备选)等腰梯形存在性问题
例、已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2。若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。(1)求点C的坐标;(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
(备选)菱形与正方形问题
例、如图,在平面直角坐标系中,抛物线 经过A(0,-4)、B(x1,0)、 C(x2,0)三点,且x2-x1=5.(1)求b、c的值;(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
存在性问题之几何图形问题,重点在于根据题意结合图形的判定方法来进行分类分析,然后在给学生讲解的过程中把思路调理化,剩下的问题就迎刃而解了。
下次初数培训内容: 圆的专题复习 培训师:孙梅老师 月考范围: 1、圆切线问题; 2、中点问题 3、动点问题; 4、存在性问题
中考数学复习重难点突破六探究存在性问题教学课件: 这是一份中考数学复习重难点突破六探究存在性问题教学课件,共9页。PPT课件主要包含了EF为腰等内容,欢迎下载使用。
中考总复习数学 专题 8 二次函数中的存在性问题课件: 这是一份中考总复习数学 专题 8 二次函数中的存在性问题课件,共60页。PPT课件主要包含了专题解析,典型例析,·1·,强化训练,·2·,·3·,·4·,·17·,·26·,·22·等内容,欢迎下载使用。
初中数学中考复习 微专题五 二次函数中的存在性问题课件PPT: 这是一份初中数学中考复习 微专题五 二次函数中的存在性问题课件PPT,共37页。PPT课件主要包含了自主解答略等内容,欢迎下载使用。












