




所属成套资源:【中考二轮】最新中考数学思想方法讲与练专题(全国通用)
最新中考数学思想方法讲与练 【猜想归纳】图案规律中的猜想归纳思想
展开
这是一份最新中考数学思想方法讲与练 【猜想归纳】图案规律中的猜想归纳思想,文件包含中考数学思想方法讲与练猜想归纳图案规律中的猜想归纳思想教师版docx、中考数学思想方法讲与练猜想归纳图案规律中的猜想归纳思想学生版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
图案规律中的猜想归纳思想
知识方法精讲
1.规律型:图形的变化类
图形的变化类的规律题
首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
2.认识图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
(3)重点和难点突破:
结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.能区分立体图形与平面图形,立体图形占有一定空间,各部分不都在同一平面内.
猜想归纳思想
归纳猜想类问题也是探索规律型问题,这类问题一般给出一组具有某种有规律的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,通过认真观察、分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论。考查学生的归纳、概括、类比能力。有利于培养学生思维的深刻性和创造性。
解决归纳猜想类问题的基本思路是“观察→归纳→猜想→证明(验证)”,具体做法:
(1)认真观察所给的一组数、式、图等,发现它们之间的关系;
(2)根据它们之间的关系分析、概括,归纳它们的共性和蕴含的变化规律,猜想得出一个一般性的结论;
(3)结合题目所给的材料情景证明或验证结论的正确性。
归纳猜想类问题可以分成四大类:
(1)数式归纳猜想题
这类题通常是先给出一组数或式子,通过观察、归纳这组数或式子的共性规律,写出一个一般性的结论。找出题目中规律,即不变的和变化的,变化的部分与序号的关系是解这类题的关键。
(2)图形归纳猜想题
此类题通常给出一组图形的排列(或操作得到一系列的图形)探求图形的变化规律,以图形为载体考查图形所蕴含的数量关系。其解题关键是找出相邻两个图形之间的位置关系和数量关系。
(3)结论归纳猜想题
结论归纳猜想题常考数值结果、数量关系及变化情况。发现或归纳出周期性或规律性变化,是解题的关键。
(4)类比归纳猜想题
类比归纳猜想题通常是指由两类对象的具有某些相同或相似的性质,和其中一类对象的某些已知的性质,推断出另一类对象也具有这些性质的一种题型,有时也指两个对象在研究方法、学习过程上类比,考查类比归纳推理能力。
一.选择题(共19小题)
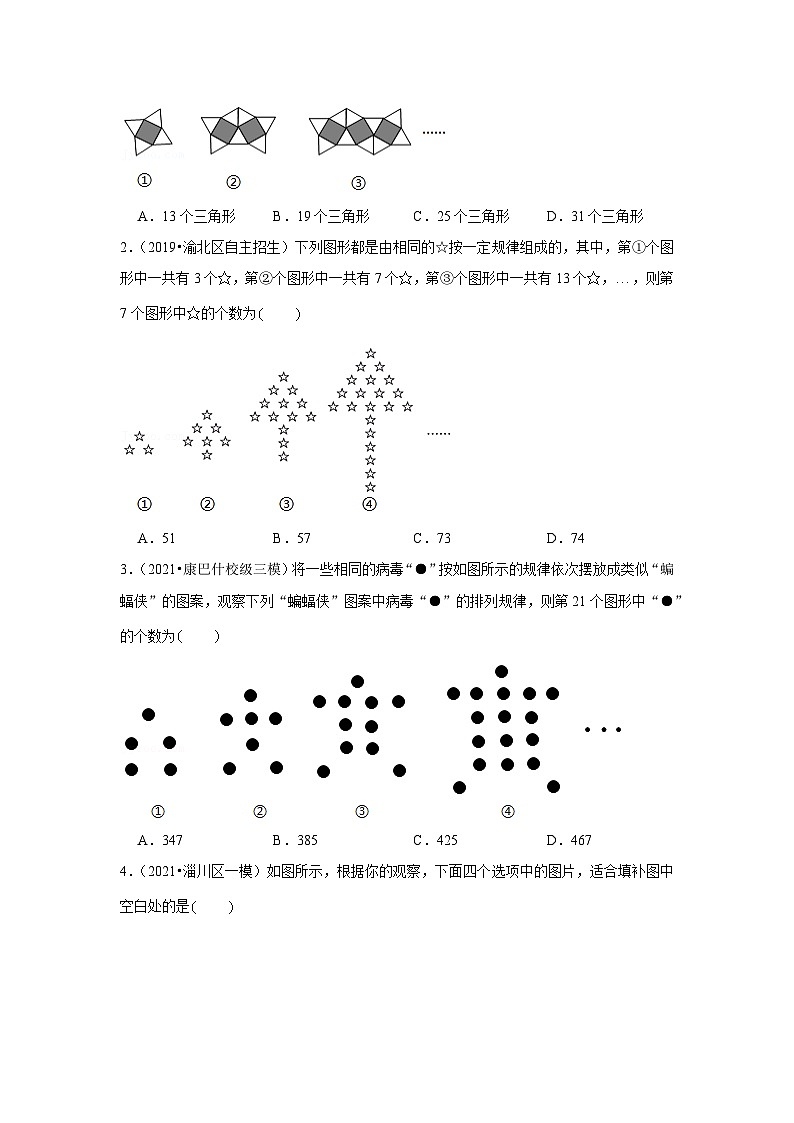
1.(2021•巴南区自主招生)把四边形和三角形按如图所示的规律拼图案,其中图案①中共有4个三角形,图案②中共有7个三角形,图案③中共有10个三角形,,若按此规律拼图案,则图案⑧中共有
A.13个三角形B.19个三角形C.25个三角形D.31个三角形
2.(2019•渝北区自主招生)下列图形都是由相同的☆按一定规律组成的,其中,第①个图形中一共有3个☆,第②个图形中一共有7个☆,第③个图形中一共有13个☆,,则第7个图形中☆的个数为
A.51B.57C.73D.74
3.(2021•康巴什校级三模)将一些相同的病毒“●”按如图所示的规律依次摆放成类似“蝙蝠侠”的图案,观察下列“蝙蝠侠”图案中病毒“●”的排列规律,则第21个图形中“●”的个数为
A.347B.385C.425D.467
4.(2021•淄川区一模)如图所示,根据你的观察,下面四个选项中的图片,适合填补图中空白处的是
A.B.C.D.
5.(2021•泗水县一模)将一列有理数,2,,4,,6,,如图所示有序排列.根据图中的排列规律可知,有理数4在“峰1”中的处.则有理数在
A.峰处B.峰处C.峰处D.峰处
6.(2021•渝中区校级三模)用大小相同的圆点摆成如图所示的图案,按照这样的规律摆放,则第8个图案中共有圆点的个数是
A.34B.40C.49D.59
7.(2021•江北区校级模拟)下列图形是用棋子按照一定规律摆成的,第①个图中有2枚棋子,第②个图中有6枚棋子,第③个图中有12枚棋子,,按照这种摆法,第8个图形中共有棋子
A.42B.56C.64D.72
8.(2021•九龙坡区模拟)下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,,按此规律排列下去,第⑦个图形中实心圆点的个数为
A.19B.20C.22D.23
9.(2021秋•平阴县期末)将全体自然数按下面的方式进行排列,按照这样的排列规律,2022应位于
A.位B.位C.位D.位
10.(2021秋•中原区校级期末)找出以下图形变化的规律,则第2022个图形中黑色正方形的数量是( )
A.3030B.3031C.3032D.3033
11.(2021秋•泉州期末)如图所示的数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第行有个数,且两端的数均为,每个数是它下一行左右相邻两数的和,若用表示第行从左到右第个数,如表示的数是,表示的数是,表示的数是,则表示的数是
A.B.C.D.
12.(2021秋•秦淮区期末)在某多媒体电子杂志的某一期上刊登了“正方形雪花图案的形成”的演示案例:作一个正方形,设每边长为,将每边四等分,作一凸一凹的两个边长为的小正方形,得到图形如图(2)所示,称为第一次变化,再对图(2)的每个边做相同的变化,得到图形如图(3),称为第二次变化,如此连续作几次,便可得到一个绚丽多彩的雪花图案.如不断发展下去到第次变化时,图形的面积和周长分别为
A.和B.和C.和D.和
13.(2021秋•顺德区期末)用木棒按如图所示的规律摆放图形,第100个图形需要木棒根数是
A.501B.502C.503D.504
14.(2021秋•丰台区期末)如图是用棋子摆成的图案,按照这样的规律摆下去,第⑨个图案需要的棋子个数为
A.81B.91C.109D.111
15.(2021秋•新都区期末)用火柴棒按如图所示的方式摆大小不同的“3”,按此规律摆下去,第2021个“3”需要火柴棒的根数为
A.4045B.6065C.6068D.8085
16.(2021秋•锦江区校级期末)如图,用菱形纸片按照如下规律拼成下列图案,若第个图案中有2021张纸片,则的值为
A.503B.504C.505D.506
17.(2021秋•西山区期末)将正方形做如下操作,第1次分别连接各边中点如图2,得到5个正方形;第2次将图2左上角正方形按上述方法再分割如图3,得到9个正方形,以此类推,根据以上操作,若要得到2025个正方形,则需要操作的次数为
A.503B.504C.505D.506
18.(2021秋•嵩县期末)有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为第一次“生长”(如图;再分别以这两个正方形的边为斜边,向外各自作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为第二次“生长”(如图如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是
A.1B.2020C.2021D.2022
19.(2021秋•大埔县期末)如图所示,直线,相交于点,“阿基米德曲线”从点开始生成,如果将该曲线与每条射线的交点依次标记为1,,3,,5,.那么标记为“2021”的点在
A.射线上B.射线上C.射线上D.射线上
二.填空题(共6小题)
20.(2020•通辽)如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形,按这样的方法拼成的第个正方形比第个正方形多 个小正方形.
21.(2021•安溪县模拟)北京天坛的国丘坛为古代祭天的场所,如图所示分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石) 环.
22.(2021•五华区一模)如图所示,下列各图形是由大小相同的黑点组成,图1中有2个点,图2中有7个点,图3中有14个点,,按此规律,那么图8中黑点的个数是 .
23.(2021•大庆模拟)把黑色三角形按如图所示的规律拼图案,其中第1个图案中有1个黑色三角形,第2个图案中有3个黑色三角形,第3个图案中有6个黑色三角形按此规律排列下去,则第5个图案中黑色三角形的个数为 个.
24.(2021•黔东南州模拟)如图是由同样大小的圆按一定规律排列所组成的,其中第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆按此规律排列下去,第10个图形中圆的个数是 个.
25.(2021秋•大同期末)观察下列图形,它们是按一定规律排列的,依照此规律,第个图形中★的个数为 .
三.解答题(共3小题)
26.(2021•胶州市一模)问题提出:
如果在一个平面内画出条直线,最多可以把这个平面分成几部分?
问题探究:
为解决问题,我们经常采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进到复杂的情形,在探究的过程中,通过归纳得出一般性的结论,进而拓展应用.
探究一:
如图1,当在平面内不画条)直线时,显然该平面只有1部分,可记为.
探究二:
如图2,当在平面内画1条直线时,该平面最多被分成了2部分,比前一次多了1部分,可记为(1).
探究三:
当在平面内画2条直线,若两条直线平行(如图,该平面被分成3部分;若两条直线相交(如图,交点将第2条直线分成2段,每一段将平面多分出1部分,因此比前一次多2部分,该平面被分成4部分,因此当在平面内画2条直线时,该平面最多被分成4部分,可记为(2),我们获得的直接经验是:直线相交时,平面被分成的部分多.
探究四:
当在平面内画3条直线,若3条直线相交于一点(如图,该平面被分成6部分;若3条直线的交点都不相同时(如图,第3条直线与前两条直线有2个交点,该直线被2个交点分成了3段,每段将平面多分出1部分,所以比前一次多出3部分,该平面被分成7部分.因此当在平面内画3条直线时,该平面最多被分成7部分,可记为(3).我们获得的经验是:直线相交的交点个数越多,平面被分成的部分就越多.所以直接探索直线交点个数最多的情况即可.
探究五:
当在平面内画4条直线(如图,第4条直线与前3条直线有3个交点,该直线被3个交点分成了4段,每段将平面多分出1部分,所以比前一次多出4部分,该平面被分成11部分.因此当在平面内画4条直线时,该平面最多被分成11部分,可记为(4).
探究六:
在平面内画5条直线,最多可以把这个平面分成几部分?(仿照前面的探究方法,写出解答过程,不需画图)
问题解决:
如果在一个平面内画出条直线,最多可以把这个平面分成 部分.
应用与拓展:
(1)如果一个平面内的10条直线将平面分成了50个部分,再增加2条直线,则该平面至多被分成 个部分.
(2)如果一个平面被直线分成了497部分,那么直线的条数至少有 条.
(3)一个正方体蛋糕切5刀,被分成的块数至多为 块.
27.(2021•芜湖模拟)把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形按此规律排列下去,解答下列问题:
(1)填写下列表格:
若第个图案中黑色三角形的个数有91个,求的值.
28.(2021•安徽模拟)观察下列图形与等式:
(1)观察图形,写出第(7)个等式: ;根据图中规律,写出第个图形的规律: ;(用含有的式子表示)
(2)求出的值.图序
①
②
③
④
黑色三角形个数
1
3
6
相关试卷
这是一份最新中考数学思想方法讲与练 【猜想归纳】周长面积问题中的猜想归纳思想,文件包含中考数学思想方法讲与练猜想归纳周长面积问题中的猜想归纳思想教师版docx、中考数学思想方法讲与练猜想归纳周长面积问题中的猜想归纳思想学生版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份最新中考数学思想方法讲与练 【猜想归纳】点的坐标中的猜想归纳思想,文件包含中考数学思想方法讲与练猜想归纳点的坐标中的猜想归纳思想教师版docx、中考数学思想方法讲与练猜想归纳点的坐标中的猜想归纳思想学生版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
这是一份2024年中考数学压轴题专项练习—猜想归纳思想,文件包含82猜想归纳思想答案docx、82猜想归纳思想docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。









