【专项复习】高考数学 专题13 双曲线 (名校模拟汇编).zip

这是一份【专项复习】高考数学 专题13 双曲线 (名校模拟汇编).zip，文件包含专项复习高考数学专题13双曲线名校模拟汇编原卷版docx、专项复习高考数学专题13双曲线名校模拟汇编解析版docx等2份试卷配套教学资源，其中试卷共76页， 欢迎下载使用。

2023真题展现
考向一 双曲线的离心率
真题考查解读
近年真题对比
考向一 双曲线的渐近线方程
命题规律解密
名校模拟探源
易错易混速记/二级结论速记
考向一 双曲线的离心率
1．（2023•新高考Ⅰ•第16题）已知双曲线C：x2a2−y2b2=1（a＞0，b＞0）的左、右焦点分别为F1，F2．点A在C上，点B在y轴上，F1A→⊥F1B→，F2A→=−23F2B→，则C的离心率为 ．
【命题意图】
考查双曲线的定义、标准方程、几何性质、直线与双曲线．考查运算求解能力、逻辑推导能力、分析问题与解决问题的能力、数形结合思想、化归与转化思想．
【考查要点】
双曲线的定义、方程、性质是高考常考内容，以小题出现，常规题，难度中等．
【得分要点】
一、双曲线的定义
把平面内与两个定点F1，F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
注：1、集合语言表达式
双曲线就是下列点的集合:.常数要小于两个定点的距离．
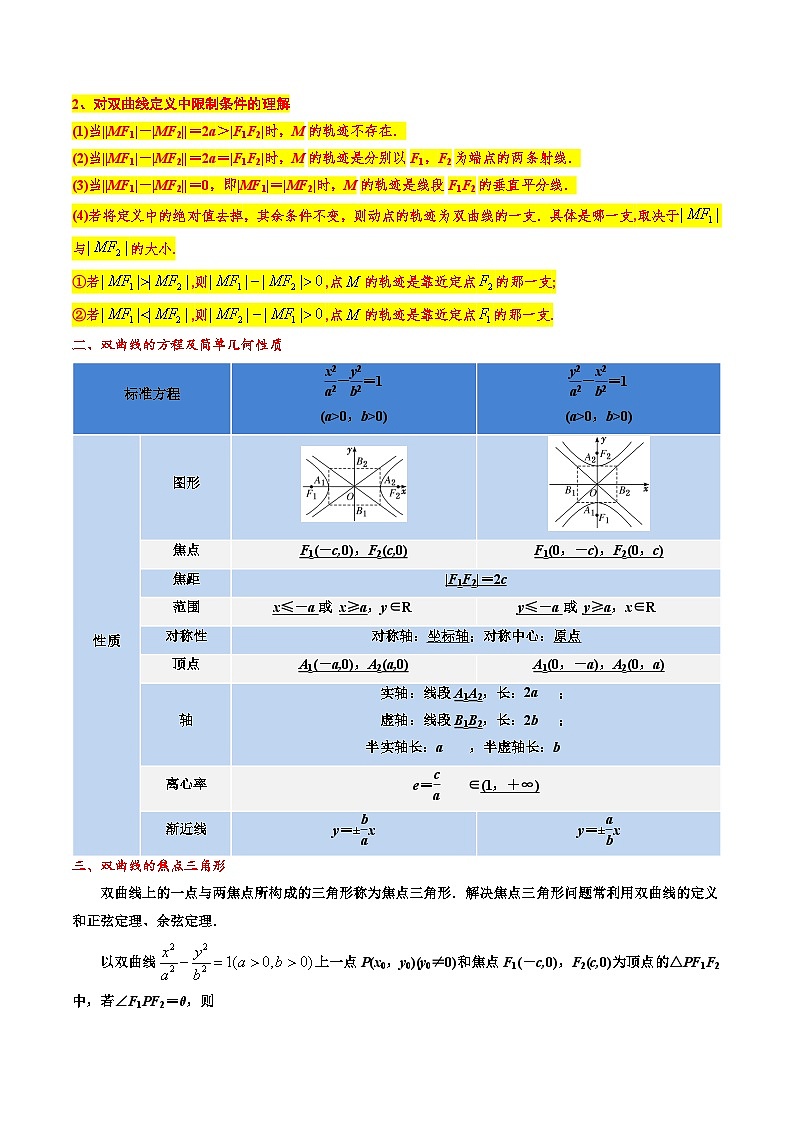
2、对双曲线定义中限制条件的理解
(1)当||MF1|－|MF2||＝2a＞|F1F2|时，M的轨迹不存在．
(2)当||MF1|－|MF2||＝2a＝|F1F2|时，M的轨迹是分别以F1，F2为端点的两条射线．
(3)当||MF1|－|MF2||＝0，即|MF1|＝|MF2|时，M的轨迹是线段F1F2的垂直平分线．
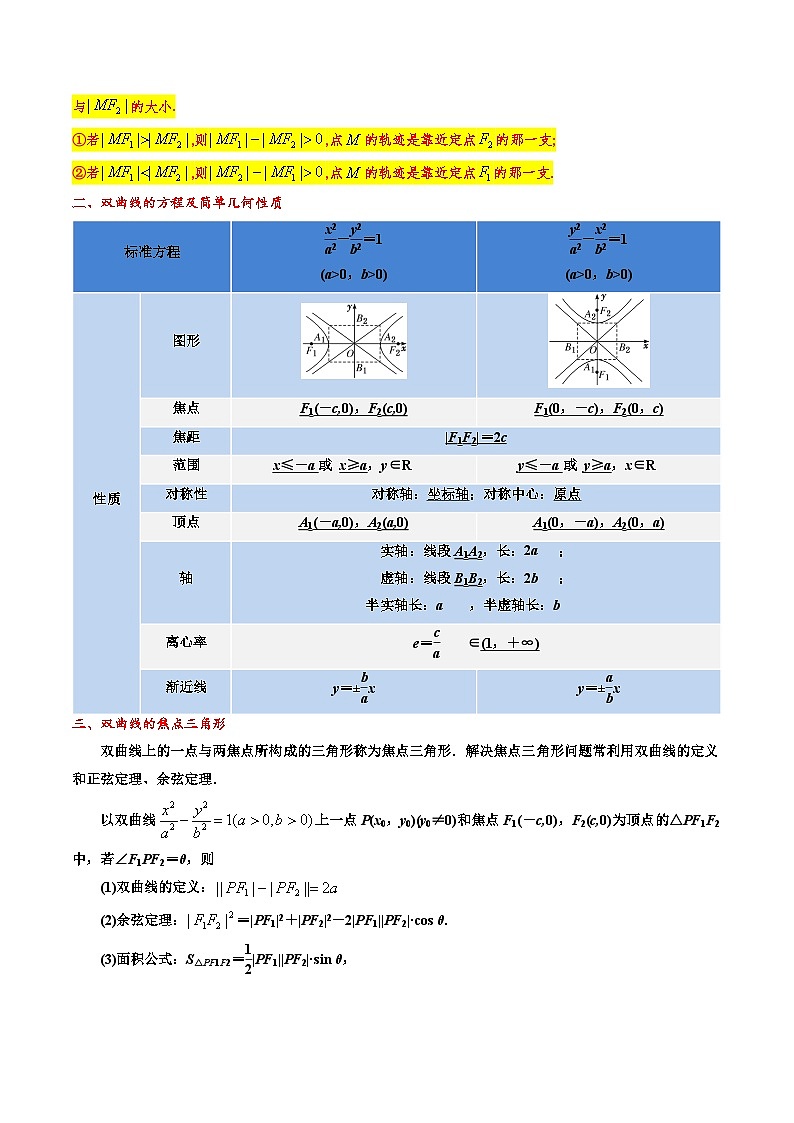
(4)若将定义中的绝对值去掉，其余条件不变，则动点的轨迹为双曲线的一支．具体是哪一支,取决于与的大小.
①若,则,点的轨迹是靠近定点的那一支;
②若,则,点的轨迹是靠近定点的那一支.
二、双曲线的方程及简单几何性质
三、双曲线的焦点三角形
双曲线上的一点与两焦点所构成的三角形称为焦点三角形．解决焦点三角形问题常利用双曲线的定义和正弦定理、余弦定理．
以双曲线上一点P(x0，y0)(y0≠0)和焦点F1(－c,0)，F2(c,0)为顶点的△PF1F2中，若∠F1PF2＝θ，则
(1)双曲线的定义：
(2)余弦定理：＝|PF1|2＋|PF2|2－2|PF1||PF2|·cs θ.
(3)面积公式：S△PF1F2＝eq \f(1,2)|PF1||PF2|·sin θ，
重要结论：S△PF1F2=
推导过程：由余弦定理得|F1F2|2=|PF1|2＋|PF2|2－2|PF1||PF2|·cs θ得
由三角形的面积公式可得
S△PF1F2=
=
四、直线与双曲线的位置关系
1、把直线与双曲线的方程联立成方程组，通过消元后化为ax2＋bx＋c＝0的形式，在a≠0的情况下考察方程的判别式．
(1)Δ>0时，直线与双曲线有两个不同的公共点．
(2)Δ＝0时，直线与双曲线只有一个公共点．
(3)Δ<0时，直线与双曲线没有公共点．
当a＝0时，此时直线与双曲线的渐近线平行，直线与双曲线有一个公共点．
注：直线与双曲线的关系中：一解不一定相切，相交不一定两解，两解不一定同支．
弦长公式
直线被双曲线截得的弦长公式，设直线与椭圆交于，两点，则

（为直线斜率）
3、通径的定义：过焦点且垂直于实轴的直线与双曲线相交于、两点，则弦长.
考向一 双曲线的渐近线方程
2．（2021•新高考Ⅱ）已知双曲线﹣＝1（a＞0，b＞0）的离心率e＝2，则该双曲线的渐近线方程为 ．
查考近几年真题推测以小题出现，常规题，难度中等．双曲线的定义、方程、性质是高考常考内容，
一．双曲线的标准方程（共5小题）
1．（2023•郑州模拟）已知双曲线（a＞0，b＞0）的离心率为2，则该双曲线的渐近线方程为（ ）
A．x±y＝0B．C．D．2x±y＝0
2．（2023•宝山区校级模拟）若双曲线经过点，且渐近线方程是，则这条双曲线的方程是 ．
3．（2023•通州区模拟）双曲线的焦点坐标为（ ）
A．（±1，0）B．（±，0）C．（±，0）D．（±，0）
4．（2023•西山区校级模拟）已知双曲线的一条渐近线的倾斜角为，则双曲线的离心率为（ ）
A．B．C．D．2
5．（2023•青羊区校级模拟）已知双曲线的右焦点为F，O为坐标原点，以OF为直径的圆与双曲线C的一条渐近线交于点O及点，则双曲线C的方程为（ ）
A．B．
C．D．
二．双曲线的性质（共33小题）
6．（2023•天山区校级模拟）已知双曲线（a＞0，b＞0）的左右焦点分别为F1、F2，过F2且垂直于x轴的直线与双曲线交于A、B两点，若△F1AB为等腰直角三角形，则该双曲线的离心率为（ ）
A．2B．C．D．
7．（2023•朝阳区一模）过双曲线的右焦点F作一条渐近线的垂线，垂足为A．若∠AFO＝2∠AOF（O为坐标原点），则该双曲线的离心率为（ ）
A．B．C．2D．或2
8．（2023•博白县模拟）已知F1，F2分别是双曲线C：﹣＝1（a＞0，b＞0）的左、右焦点，P为双曲线右支上一点，若∠F1PF2＝60°，＝ac，则双曲线的离心率为（ ）
A．B．C．D．2
9．（2023•郑州模拟）点（4，0）到双曲线Γ：的一条渐近线的距离为，则双曲线的离心率为（ ）
A．B．C．D．5
10．（2023•武鸣区校级二模）双曲线x2﹣＝1的焦点坐标为（ ）
A．（±1，0）B．（0，±）C．（±，0）D．（0，±1）
11．（2023•河南模拟）已知双曲线的左、右焦点分别为F1，F2，P是双曲线C的一条渐近线上的点，且线段PF1的中点M在另一条渐近线上．若∠PF2F1＝45°，则双曲线C的离心率为（ ）
A．B．C．2D．
12．（2023•源汇区校级模拟）已知F1、F2分别为双曲线＝1（a＞0，b＞0）的左、右焦点，P为双曲线右支上任意一点，若的最小值为2c，c＝，则该双曲线的离心率是（ ）
A．3B．4C．D．
13．（2023•四川模拟）已知双曲线C：x2﹣＝1（a＞b＞0）的左，右顶点分别为A，B，点P在双曲线C上，过点B作x轴的垂线BM，交PA于点M．若∠PAB＝∠PBM，则双曲线C的离心率为（ ）
A．B．C．2D．3
14．（2023•贺兰县校级模拟）人们在进行工业设计时，巧妙地利用了圆锥曲线的光学性质．从双曲线右焦点F2发出的光线通过双曲线镜面反射出发散光线，且反射光线的反向延长线经过左焦点F1.已知双曲线的方程为x2﹣y2＝1，则当入射光线F2P和反射光线PE互相垂直时（其中P为入射点），∠F1F2P的余弦值大小为（ ）
A．B．C．D．
15．（2023•海淀区校级模拟）若双曲线的一条渐近线被圆（x﹣2）2+y2＝4所截得的弦长为，则双曲线C的离心率为（ ）
A．B．C．D．
16．（2023•广西模拟）双曲线C：（a＞0，b＞0）的左顶点为A，点P，Q均在C上，且关于y轴对称．若直线AP，AQ的斜率之积为，则C的离心率为（ ）
A．B．C．2D．
17．（2023•未央区模拟）设O为坐标原点，F1，F2是双曲线C：的左、右焦点，已知双曲线C的离心率为，过F2作C的一条渐近线的垂线，垂足为P，则＝（ ）
A．B．2C．D．
18．（2023•贵阳模拟）已知双曲线C：mx2﹣ny2＝1（m＞0，n＞0）的离心率为，虚轴长为4，则C的方程为（ ）
A．3x2﹣4y2＝1B．
C．D．
19．（2023•郑州模拟）已知双曲线的左焦点为F，过原点O的直线与C交于点A，B，若|OF|＝|OA|，则|AF||BF|＝（ ）
A．2B．4C．8D．16
20．（2023•蕉城区校级二模）已知双曲线的左、右焦点分别为F1、F2，过F2的直线l交双曲线的右支于A、B两点．点M满足，且，者，则双曲线的离心率是（ ）
A．B．C．D．
21．（2023•凉山州模拟）已知以直线y＝±2x为渐近线的双曲线，经过直线x+y﹣3＝0与直线2x﹣y+6＝0的交点，则双曲线的实轴长为（ ）
A．6B．C．D．8
22．（2023•滨海新区校级三模）点F是抛物线x2＝8y的焦点，A为双曲线C：的左顶点，直线AF平行于双曲线C的一条渐近线，则实数b的值为（ ）
A．2B．4C．8D．16
23．（2023•恩施市校级模拟）已知F1，F2分别为双曲线C：的左右焦点，且F1到渐近线的距离为1，过F2的直线l与C的左、右两支曲线分别交于A，B两点，且l⊥AF1，则下列说法正确的为（ ）
A．△AF1F2的面积为2B．双曲线C的离心率为
C．D．
24．（2023•郑州模拟）已知F1，F2分别是双曲线Γ：的左、右焦点，过F1的直线分别交双曲线左、右两支于A，B两点，点C在x轴上，，BF2平分∠F1BC，则双曲线Γ的离心率为（ ）
A．B．C．D．
25．（2023•沙坪坝区校级模拟）已知双曲线C：的左、右焦点分别为F1，F2，过双曲线C上一点P向y轴作垂线，垂足为Q，若|PQ|＝|F1F2|且PF1与QF2垂直，则双曲线C的离心率为（ ）
A．B．C．D．
26．（2023•林芝市二模）已知双曲线的左、右焦点分别是F1，F2，双曲线C上有两点A，B满足，且，若四边形F1AF2B的周长l与面积S满足，则双曲线C的离心率为（ ）
A．B．C．D．
27．（2023•安徽模拟）在平面直角坐标系xOy中，已知双曲线的左、右焦点分别为F1，F2，过F1的直线与双曲线C的右支相交于点P，过点O，F2作ON⊥PF1，F2M⊥PF1，垂足分别为N，M，且M为线段PN的中点，|ON|＝a，则双曲线C的离心率为（ ）
A．2B．C．D．
28．（2023•长沙模拟）已知双曲线4x2﹣＝1的左、右焦点分别为F1，F2，点M是双曲线右支上一点，满足•＝0，点N是线段F1F2上一点，满足＝λ．现将△MF1F2沿MN折成直二面角F1﹣MN﹣F2，若使折叠后点F1，F2距离最小，则λ＝（ ）
A．B．C．D．
29．（2023•濠江区校级模拟）已知双曲线的右焦点为F，过点F且斜率为k（k≠0）的直线l交双曲线于A、B两点，线段AB的中垂线交x轴于点D．若，则双曲线的离心率取值范围是（ ）
A．B．C．D．
30．（2023•洛阳模拟）已知双曲线C：的左、右焦点分别为F1（﹣c，0），F2（c，0），过点F1的直线l与双曲线C的左支交于点A，与双曲线C的一条渐近线在第一象限交于点B，且|F1F2|＝2|OB|（O为坐标原点）．下列四个结论正确的是（ ）
①；
②若，则双曲线C的离心率；
③|BF1|﹣|BF2|＞2a；
④．
A．①②B．①③C．①②④D．①③④
31．（2023•江西二模）已知双曲线E：，其左右顶点分别为A1，A2，P在双曲线右支上运动，若∠A1PA2的角平分线交x轴于D点，A2关于PD的对称点为A3，若仅存在2个P使直线A3D与E仅有一个交点，则E离心率的范围为（ ）
A．B．C．D．（2，+∞）
32．（2023•江西模拟）双曲线的左焦点为F，过点F的直线l与双曲线C交于A，B两点，若过A，B和点的圆的圆心在y轴上，则直线l的斜率为（ ）
A．B．C．±1D．
33．（多选）（2023•宜章县模拟）已知F1，F2分别为双曲线C：＝1（a＞0，b＞0）的左、右焦点，P为双曲线C的渐近线在第一象限部分上的一点，线段PF2与双曲线交点为Q，且|F1P|＝|F1F2|＝2|PF2|，O为坐标原点，则下列结论正确的是（ ）
A．|OP|＝2a
B．双曲线C的离心率e＝
C．|QF1|＝a
D．若△QF1F2的内心的横坐标为3，则双曲线C的方程为＝1
34．（2023•万州区校级模拟）已知F1，F2为双曲线C：＝1（a＞0，b＞0）的左右焦点，过点F1作一条渐近线的垂线交双曲线右支于点P，直线PF2与y轴交于点Q（P，Q在x轴同侧），连接QF1，如图，若△PQF1内切圆圆心恰好落在以F1F2为直径的圆上，则∠F1PF2＝ ；双曲线的离心率e＝ ．
35．（2023•淮北一模）已知双曲线C：过点，则其方程为 ，设F1，F2分别为双曲线C的左右焦点，E为右顶点，过F2的直线与双曲线C的右支交于A，B两点（其中点A在第一象限），设M，N分别为△AF1F2，△BF1F2的内心，则|ME|﹣|NE|的取值范围是 ．
36．（多选）（2023•芜湖模拟）双曲线的光学性质：从双曲线一个焦点出发的光线，经双曲线反射后，反射光线的反向延长线经过双曲线的另一个焦点．已知O为坐标原点，F1，F2分别是双曲线C：的左右焦点，过F2的直线交双曲线C的右支于M，N两点，且M（x1，y1）在第一象限，△MF1F2，△NF1F2的内心分别为I1，I2，其内切圆半径分别为r1，r2，△MF1N的内心为I．双曲线C在M处的切线方程为，则下列说法正确的有（ ）
A．点I1、I2均在直线x＝3上
B．直线MI的方程为
C．
D．
37．（多选）（2023•广东模拟）双曲线的左右焦点分别为F1，F2，P为双曲线右支上异于顶点的一点，△PF1F2的内切圆记为圆I，圆I的半径为r，过F1作PI的垂线，交PI的延长线于Q，则（ ）
A．动点I的轨迹方程为x＝4（y≠0）
B．r的取值范围为（0，3）
C．若r＝1，则tan∠F1PF2＝
D．动点Q的轨迹方程为x2+y2＝16（x≠4且x＞﹣）
38．（2023•赤峰模拟）初中时代我们就说反比例函数的图像是双曲线，建立适当的平面直角坐标系可以求得这个双曲线的标准方程，比如，把的图象顺时针旋转可以得到双曲线．已知函数，在适当的平面直角坐标系中，其标准方程可能是（ ）
A．B．
C．D．
三．直线与双曲线的综合（共22小题）
39．（2023•射洪市校级模拟）已知双曲线的右焦点为F，点A（0，m），若直线AF与C只有一个交点，则m＝（ ）
A．±2B．C．D．±4
40．（2023•赤峰三模）2022年卡塔尔世界杯中的数字元素——会徽（如图）正视图近似伯努利双纽线．定义：在平面直角坐标系xOy中，把到定点F1（﹣a，0）F2（a，0）的距离之积等于a2（a＞0）的点的轨迹称为双纽线C．已知P（x0，y0）是双纽线C上的一点，下列说法错误的是（ ）
A．双纽线C关于原点O成中心对称
B．
C．双曲线C上满足|PF1|＝|PF2|的点P有两个
D．|OP|的最大值为
41．（2023•淮北二模）已知A（﹣2，0），B（2，0），过P（0，﹣1）斜率为k的直线上存在不同的两个点M，N满足：．则k的取值范围是（ ）
A．
B．
C．
D．
42．（2023•河南模拟）设双曲线的左、右焦点分别为F1，F2，B为双曲线E上在第一象限内的点，线段F1B与双曲线E相交于另一点A，AB的中点为M，且F2M⊥AB，若∠AF1F2＝30°，则双曲线E的离心率为（ ）
A．B．2C．D．
43．（2023•天津模拟）双曲线的左右焦点分别是F1，F2，离心率为e，过点F1的直线交双曲线的左支于M，N两点．若△MF2N是以M为直角顶点的等腰直角三角形，则e2等于（ ）
A．B．C．D．
44．（2023•让胡路区校级模拟）已知双曲线的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点，若A为线段BF1的中点，且BF1⊥BF2，则C的离心率为（ ）
A．B．2C．D．3
45．（2023•江西模拟）已知双曲线C：＝1，若直线l：y＝kx+t（kt≠0）与双曲线C交于不同的两点P，Q，且P，Q与M（0，1）构成的三角形中有∠MPQ＝∠MQP，则t的取值范围是（ ）
A．（﹣∞，﹣3）∪（0，+∞）B．
C．D．
46．（2023•咸阳一模）直线l过双曲线C：＝1（a＞0，b＞0）的右焦点F，与双曲线C的两条渐近线分别交于A，B两点，O为原点，且•＝0，3＝，则双曲线C的离心率为（ ）
A．B．C．D．
47．（2023•包河区校级模拟）设点F为双曲线的左焦点，经过原点O且斜率的直线与双曲线C交于A、B两点，AF的中点为P，BF的中点为Q．若OP⊥OQ，则双曲线C的离心率e的取值范围是 ．
48．（2023•宜宾模拟）已知双曲线C：的左，右焦点分别为F1，F2，离心率为，过F2作渐近线的垂线交C于A，B两点，点A在第一象限，若，则△ABF1的周长为 ．
49．（2023•山东模拟）过双曲线x2﹣y2＝1的左、右焦点作两条相互平行的弦AB，CD，其中A，B在双曲线的左支上，A，C在x轴上方，则|AF1|⋅|CF2|的最小值为 ，当AB的倾斜角为时，四边形AF1F2C的面积为 ．
50．（2023•黄石模拟）三等分角是古希腊三大几何难题之一．公元3世纪末，古希腊数学家帕普斯利用双曲线解决了三等分角问题如图，已知圆心角ACB是待三等分的角（0＜∠ACB＜π）具体操作方法如下：在弦AB上取一点D，满足AD＝2DB，以AD为实轴，为虚轴作双曲线，交圆弧AB于点M，则∠ACM＝2∠MCB，即CM为∠ACB的三等分线已知双曲线E的方程为，点A，D分别为双曲线E的左，右顶点，点B为其右焦点，点C为双曲线E的右准线上一点，且不在x轴上，线段CB交双曲线E于点P若扇形CMB的面积为，则的值为 ．
51．（2023•九江模拟）过点A（0，1）作斜率为k的直线l交双曲线于P1，P2两点，线段P1P2的中点在直线上，则实数k的值为 ．
52．（2023•嘉定区模拟）定义两个点集S、T之间的距离集为d（S，T）＝{|PQ||P∈S，Q∈T}，其中|PQ|表示两点P、Q之间的距离，已知k、t∈R，S＝{（x，y）|y＝kx+t，x∈R}，，若d（S，T）＝（1，+∞），则t的值为 ．
53．（2023•思明区校级模拟）设F为双曲线E：＝1（a＞0，b＞0）的右焦点，A，B分别为双曲线E的左右顶点，点P为双曲线E上异于A，B的动点，直线l：x＝t使得过F作直线AP的垂线交直线l于点Q时总有B，P，Q三点共线，则的最大值为 ．
54．（多选）（2023•广州二模）已知双曲线Γ：x2﹣y2＝a2（a＞0）的左，右焦点分别为F1，F2，过F2的直线l与双曲线Γ的右支交于点B，C，与双曲线Γ的渐近线交于点A，D（A，B在第一象限，C，D在第四象限），O为坐标原点，则下列结论正确的是（ ）
A．若BC⊥x轴，则△BCF1的周长为6a
B．若直线OB交双曲线Γ的左支于点E，则BC∥EF1
C．△AOD面积的最小值为4a2
D．|AB|+|BF1|的取值范围为（3a，+∞）
55．（2023•海珠区校级三模）在平面上给定相异两点A，B，设点P在同一平面上且满足＝λ，当λ＞0且λ≠1时，P点的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故我们称这个圆为阿波罗尼斯圆．现有双曲线＝1（a＞0，b＞0），F1，F2分别为双曲线的左、右焦点，A，B为双曲线虚轴的上、下端点，动点P满足＝2，△PAB面积的最大值为4．点S，T在双曲线上，且关于原点O对称，Q是双曲线上一点，直线QS和QT的斜率满足kQS•kQT＝3，则双曲线方程是 ；过F2的直线与双曲线右支交于C，D两点（其中C点在第一象限），设点M、N分别为△CF1F2、△DF1F2的内心，则|MN|的范围是 ．
56．（2023•贵州模拟）已知双曲线E的焦点为F1（﹣1，0），F2（1，0），过F1的直线l1与E的左支相交于A，B两点，过F2的直线l2与E的右支相交于C，D两点，若四边形ABCD为平行四边形，以AD为直径的圆过F1，|DF1|＝|AF1|，则E的方程为（ ）
A．2x2﹣2y2＝1B．
C．D．
57．（2023•江西模拟）已知F双曲线的右焦点，A1，A2分别是双曲线C的左右顶点，过F作双曲线渐近线的垂线与该渐近线在第一象限的交点为M，直线A1M交C的右支于点P，若|MP|＝|MA2|，且，则C的离心率为（ ）
A．B．C．2D．
58．（2023•福建模拟）双曲线的下焦点为F，过F的直线l与C交于A，B两点，若过A，B和点的圆的圆心在x轴上，则直线l的斜率为（ ）
A．B．C．±1D．
59．（多选）（2023•合肥模拟）如图，O为坐标原点，F1，F2分别为双曲线的左、右焦点，过双曲线C右支上一点P作双曲线的切线l分别交两渐近线于A、B两点，交x轴于点D，则下列结论正确的是（ ）
A．|AB|min＝2b
B．S△AOB＝2S△AOP
C．S△AOB＝2b
D．若存在点P，使得，且，则双曲线C的离心率为2或
60．（多选）（2023•南通模拟）已知F1，F2是双曲线的左、右焦点，是C上一点，若C的离心率为，连结AF2交C于点B，则（ ）
A．C的方程为
B．∠F1AF2＝90°
C．△F1AF2的周长为
D．△ABF1的内切圆半径为
双曲线常用结论：
(1)如图：①动点P到同侧焦点F2的距离最小值为：|PF2|最小＝|A2F2|＝c－a；
②焦点到渐近线的距离为：|F2M|＝b；
(2)渐近线求法结论：可直接令方程eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ≠0)等号右边的常数为0，化简解得；
标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1
(a>0，b>0)
eq \f(y2,a2)－eq \f(x2,b2)＝1
(a>0，b>0)
性质
图形
焦点
F1(－c,0)，F2(c,0)
F1(0，－c)，F2(0，c)
焦距
|F1F2|＝2c
范围
x≤－a或 x≥a，y∈eq \a\vs4\al(R)
y≤－a或 y≥a，x∈eq \a\vs4\al(R)
对称性
对称轴：坐标轴；对称中心：原点
顶点
A1(－a,0)，A2(a,0)
A1(0，－a)，A2(0，a)
轴
实轴：线段A1A2，长：eq \a\vs4\al(2a)；
虚轴：线段B1B2，长：eq \a\vs4\al(2b)；
半实轴长：eq \a\vs4\al(a)，半虚轴长：eq \a\vs4\al(b)
离心率
e＝eq \a\vs4\al(\f(c,a))∈(1，＋∞)
渐近线
y＝±eq \f(b,a)x
y＝±eq \f(a,b)x