初中数学——九大几何模型学案
展开
这是一份初中数学——九大几何模型学案,共16页。
等边三角形
【条件】:△OAB和△OCD均为等边三角形;
【结论】:①△OAC≌△OBD;②∠AEB=60°;③OE平分∠AED
等腰直角三角形
【条件】:△OAB和△OCD均为等腰直角三角形;
【结论】:①△OAC≌△OBD;②∠AEB=90°;③OE平分∠AED
顶角相等的两任意等腰三角形
【条件】:△OAB和△OCD均为等腰三角形;
且∠COD=∠AOB
【结论】:①△OAC≌△OBD;
②∠AEB=∠AOB;
③OE平分∠AED
模型二:手拉手模型----旋转型相似
一般情况
【条件】:CD∥AB,
将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA
特殊情况
【条件】:CD∥AB,∠AOB=90°
将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA;
③tan∠OCD;④BD⊥AC;
⑤连接AD、BC,必有;⑥
模型三、对角互补模型
全等型-90° 更多资料及电子版在公众号:学习笔记君
【条件】:①∠AOB=∠DCE=90°;②OC平分∠AOB
【结论】:①CD=CE;②OD+OE=OC;③
证明提示:
①作垂直,如图2,证明△CDM≌△CEN
②过点C作CF⊥OC,如图3,证明△ODC≌△FEC
※当∠DCE的一边交AO的延长线于D时(如图4):
以上三个结论:①CD=CE;②OE-OD=OC;
③
全等型-120°
【条件】:①∠AOB=2∠DCE=120°;②OC平分∠AOB
【结论】:①CD=CE;②OD+OE=OC;③
证明提示:①可参考“全等型-90°”证法一;
②如右下图:在OB上取一点F,使OF=OC,证明△OCF为等边三角形。
全等型-任意角ɑ
【条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE;
【结论】:①OC平分∠AOB;②OD+OE=2OC·csɑ;
③
※当∠DCE的一边交AO的延长线于D时(如右下图):
原结论变成:① ;
② ;
③ 。
可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。
对角互补模型总结:
①常见初始条件:四边形对角互补,注意两点:四点共圆有直角三角形斜边中线;
②初始条件“角平分线”与“两边相等”的区别;
③注意OC平分∠AOB时,
∠CDE=∠CED=∠COA=∠COB如何引导?
模型四:角含半角模型90°
角含半角模型90°---1
【条件】:①正方形ABCD;②∠EAF=45°;
【结论】:①EF=DF+BE;②△CEF的周长为正方形ABCD周长的一半;
也可以这样:
【条件】:①正方形ABCD;②EF=DF+BE;
【结论】:①∠EAF=45°;
角含半角模型90°---2
【条件】:①正方形ABCD;②∠EAF=45°;
【结论】:①EF=DF-BE;
角含半角模型90°---3
【条件】:①Rt△ABC;②∠DAE=45°;
【结论】:(如图1)
若∠DAE旋转到△ABC外部时,结论仍然成立(如图2)
角含半角模型90°变形
【条件】:①正方形ABCD;②∠EAF=45°;
【结论】:△AHE为等腰直角三角形;
证明:连接AC(方法不唯一)
∵∠DAC=∠EAF=45°,
∴∠DAH=∠CAE,又∵∠ACB=∠ADB=45°;
∴△DAH∽△CAE,∴
∴△AHE∽△ADC,∴△AHE为等腰直角三角形
模型五:倍长中线类模型
倍长中线类模型---1
【条件】:①矩形ABCD;②BD=BE;
③DF=EF;
【结论】:AF⊥CF
模型提取:①有平行线AD∥BE;②平行线间线段有中点DF=EF;
可以构造“8”字全等△ADF≌△HEF。
倍长中线类模型---2
【条件】:①平行四边形ABCD;②BC=2AB;③AM=DM;④CE⊥AB;
【结论】:∠EMD=3∠MEA
辅助线:有平行AB∥CD,有中点AM=DM,延长EM,构造△AME≌△DMF,连接CM构造
等腰△EMC,等腰△MCF。(通过构造8字全等线段数量及位置关系,角的大小转化)
模型六:相似三角形360°旋转模型
(1)相似三角形(等腰直角)360°旋转模型---倍长中线法
【条件】:①△ADE、△ABC均为等腰直角三角形;②EF=CF;
【结论】:①DF=BF;②DF⊥BF
辅助线:延长DF到点G,使FG=DF,连接CG、BG、BD,证明△BDG为等腰直角三角形;
突破点:△ABD≌△CBG;
难点:证明∠BAO=∠BCG
(2)相似三角形(等腰直角)360°旋转模型---补全法
【条件】:①△ADE、△ABC均为等腰直角三角形;②EF=CF;
【结论】:①DF=BF;②DF⊥BF
辅助线:构造等腰直角△AEG、△AHC;
辅助线思路:将DF与BF转化到CG与EF。
任意相似直角三角形360°旋转模型---补全法
【条件】:①△OAB∽△ODC;②∠OAB=∠ODC=90°;③BE=CE;
【结论】:①AE=DE;②∠AED=2∠ABO
辅助线:延长BA到G,使AG=AB,延长CD到点H使DH=CD,补全△OGB、△OCH构造旋转模型。转化AE与DE到CG与BH,难点在转化∠AED。
任意相似直角三角形360°旋转模型---倍长法
【条件】:①△OAB∽△ODC;②∠OAB=∠ODC=90°;③BE=CE;
【结论】:①AE=DE;②∠AED=2∠ABO
辅助线:延长DE至M,使ME=DE,将结论的两个条件转化为证明△AMD∽△ABO,此为难点,
将△AMD∽△ABC继续转化为证明△ABM∽△AOD,使用两边成比例且夹角相等,此处难点在证明∠ABM=∠AOD
模型七:最短路程模型
最短路程模型一(将军饮马类)
总结:右四图为常见的轴对称类最短路程问题,
最后都转化到:“两点之间,线段最短:解决;
特点:①动点在直线上;②起点,终点固定
最短路程模型二(点到直线类1)
【条件】:①OC平分∠AOB;②M为OB上一定点;③P为OC上一动点;④Q为OB上一动点;
【问题】:求MP+PQ最小时,P、Q的位置?
辅助线:将作Q关于OC对称点Q’,转化PQ’=PQ,过点M作MH⊥OA,
则MP+PQ=MP+PQ’MH(垂线段最短)
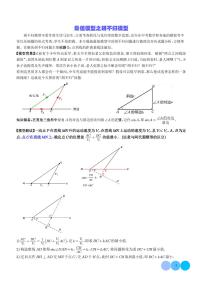
最短路程模型二(点到直线类2)
【条件】:A(0,4),B(-2,0),P(0,n)
【问题】:n为何值时,最小?
求解方法:①x轴上取C(2,0),使sin∠OAC=;②过B作BD⊥AC,交y轴于点E,即为所求;③tan∠EBO=tan∠OAC=,即E(0,1)
最短路程模型三(旋转类最值模型)
【条件】:①线段OA=4,OB=2;②OB绕点O在平面内360°旋转;
【问题】:AB的最大值,最小值分别为多少?
【结论】:以点O为圆心,OB为半径作圆,如图所示,将问题转化为
“三角形两边之和大于第三边,两边之差小于第三边”。
最大值:OA+OB;最小值:OA-OB
【条件】:①线段OA=4,OB=2;②以点O为圆心,OB,OC为半径作圆;
③点P是两圆所组成圆环内部(含边界)一点;
【结论】:若PA的最大值为10,则OC= 6 ;若PA的最小值为1,则OC= 3 ;
若PA的最小值为2,则PC的取值范围是 0
相关学案
这是一份中考数学(培优)几何模型全集(含答案)学案,共443页。
这是一份重要的几何模型之12345模型-2024年中考数学常见几何模型学案,文件包含重要的几何模型之12345模型学生版pdf、重要的几何模型之12345模型解析版pdf等2份学案配套教学资源,其中学案共31页, 欢迎下载使用。
这是一份重要的几何模型之中点模型(二)-2024年中考数学常见几何模型学案,文件包含重要的几何模型之中点模型二解析版pdf、重要的几何模型之中点模型二学生版pdf等2份学案配套教学资源,其中学案共50页, 欢迎下载使用。