

专题7二次函数与菱形存在性问题(学生版)-拔尖2023中考数学压轴题突破(全国通用)
展开我们已经知道菱形是特殊的平行四边形,它的判定方法一共有五种,分别是
①四边都相等的四边形是菱形;②两条对角线互相垂直的平行四边形是菱形 ;③邻边相等的平行四边形是菱形;④对角线互相垂直平分的四边形是菱形 ;⑤一条对角线平分一个顶角的平行四边形是菱形.
在做几何证明题的时候我们常用的判定方法主要是前三种.
二次函数和菱形存在性问题作为压轴题目,结合了“分类讨论思想”,“方程思想”“菱形的判定方法”,势必要比单纯的菱形判定思考难度要大的多,纵观历年中考真题,菱形存在性问题主要是以“两定两动”为设问方式,其中两定指的是四边形四个顶点其中有两个顶点的坐标是确定的或者是可求解的;两动指的是其中一个动点在一条直线或者抛物线上,另外一个动点是平面内任意一点或者该动点也在一条直线或者抛物线上.
【例1】(2020•雁塔区校级模拟)在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=4,抛物线与x轴相交于A(2,0),B两点,与y轴交于点C(0,6),点E为抛物线的顶点.
(1)求抛物线的函数表达式及顶点E的坐标;
(2)若将该抛物线的图象绕x轴上一点M旋转180°,点C、E的对应点分别是点C'、E',当以C、E、C'、E'为顶点的四边形是菱形时,求点M的坐标及旋转后的抛物线的表达式,
【例2】(2021•齐齐哈尔三模)如图,在平面直角坐标系中,抛物线y=ax2﹣x+c(a≠0)与x轴交于点A、B两点(点A在点B左侧),与y轴交于点C.OA、OB的长是不等式组的整数解(OA<OB),点D(2,m)在抛物线上.
(1)求抛物线的解析式及m的值;
(2)y轴上的点E使AE和DE的值最小,则OE= ;
(3)将抛物线向上平移,使点C落在点F处.当AD∥FB时,抛物线向上平移了 个单位;
(4)点M在在y轴上,平面直角坐标系内存在点N使以点A、B、M、N为顶点的四边形为菱形,请直接写出点N的坐标.
【例3】(2022•烟台)如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)求抛物线的表达式;
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
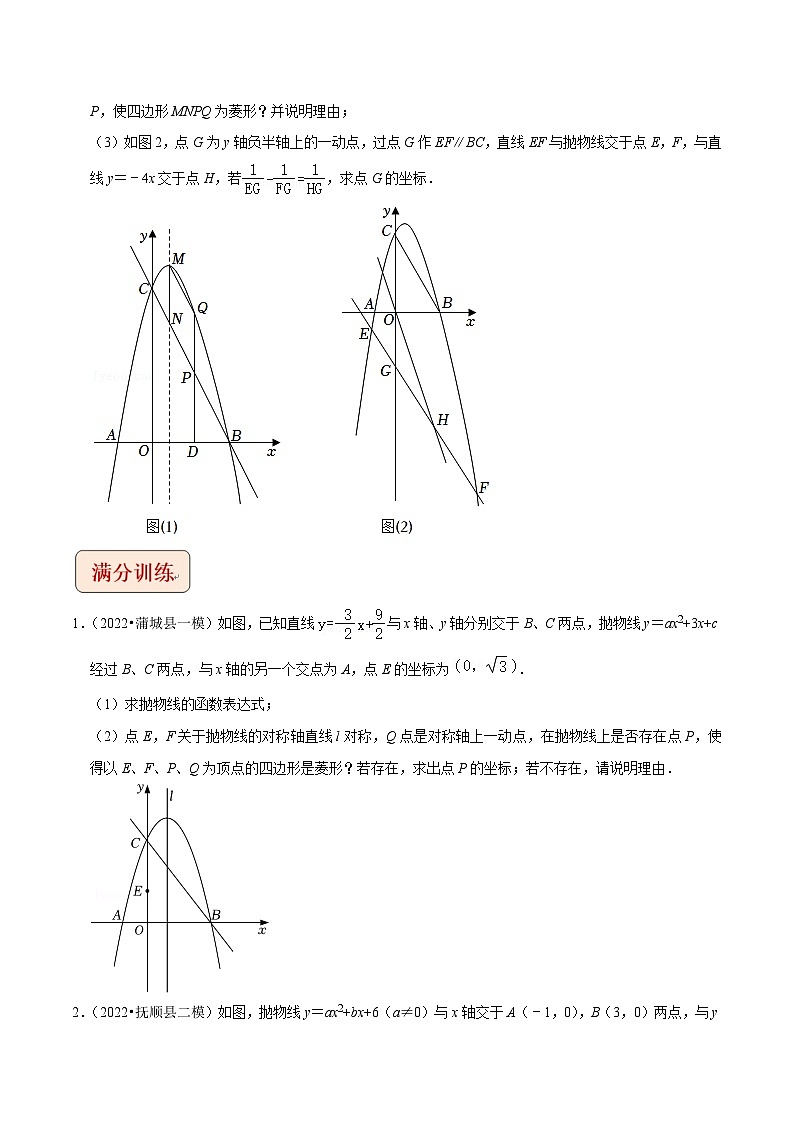
【例4】(2022•武昌区模拟)如图,直线y=﹣2x+8分别交x轴,y轴于点B,C,抛物线y=﹣x2+bx+c过B,C两点,其顶点为M,对称轴MN与直线BC交于点N.
(1)直接写出抛物线的解析式;
(2)如图1,点P是线段BC上一动点,过点P作PD⊥x轴于点D,交抛物线于点Q,问:是否存在点P,使四边形MNPQ为菱形?并说明理由;
(3)如图2,点G为y轴负半轴上的一动点,过点G作EF∥BC,直线EF与抛物线交于点E,F,与直线y=﹣4x交于点H,若,求点G的坐标.
1.(2022•蒲城县一模)如图,已知直线与x轴、y轴分别交于B、C两点,抛物线y=ax2+3x+c经过B、C两点,与x轴的另一个交点为A,点E的坐标为.
(1)求抛物线的函数表达式;
(2)点E,F关于抛物线的对称轴直线l对称,Q点是对称轴上一动点,在抛物线上是否存在点P,使得以E、F、P、Q为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
2.(2022•抚顺县二模)如图,抛物线y=ax2+bx+6(a≠0)与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求抛物线的解析式;
(2)若在线段BC上存在一点M,使得∠BMO=45°,过点O作OH⊥OM交BC的延长线于点H,求点M的坐标;
(3)点P是y轴上一动点,点Q是在对称轴上一动点,是否存在点P,Q,使得以点P,Q,C,D为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
3.(2022•历下区三模)如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象交x轴于A、B两点,与y轴交于点C,OB=3OA=3,点P是抛物线上一动点.
(1)求抛物线的解析式及点C坐标;
(2)如图1,若点P在第一象限内,过点P作x轴的平行线,交直线BC于点E,求线段PE的最大值及此时点P的坐标;
(3)如图2,过点P作x轴的垂线交x轴于点Q,交直线BC于点M,在y轴上是否存在点G,使得以M,P,C,G为顶点的四边形为菱形?若存在,请直接写出所有满足条件的点G坐标;若不存在,请说明理由.
4.(2022•碑林区校级三模)如图,在平面直角坐标系中,已知抛物线L1:y=﹣x2+bx+c经过点A(2,2),抛物线的对称轴是直线x=1,顶点为点B.
(1)求这条抛物线的解析式;
(2)将抛物线L1平移到抛物线L2,抛物线L2的顶点记为D,它的对称轴与x轴的交点记为E.已知点C(2,﹣1),若以A、C、D、E为顶点的四边形为菱形,则请求出抛物线L2的顶点坐标.
5.(2022•佛山校级三模)如图,抛物线y=ax2+bx+c与x轴交于A,B(﹣1,0)两点,与y轴交于点C,直线AC的解析式为y=x﹣2.
(1)求抛物线的解析式;
(2)已知k为正数,当0<x≤1+k时,y的最大值和最小值分别为m,n,且m+n=,求k的值;
(3)点P是平面内任意一点,在抛物线对称轴上是否存在点Q,使得以点A,C,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
6.(2022•邵阳模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求抛物线的解析式及对称轴;
(2)如图,点D与点C关于对称轴对称,点P在对称轴上,若∠BPD=90°,求点P的坐标;
(3)点M是抛物线上一动点,点N在抛物线的对称轴上,是否存在以A、B、M、N为顶点的四边形为菱形,若存在,求出点N的坐标;若不存在,请说明理由.
7.(2022•九龙坡区模拟)如图1,抛物线y=ax2+bx+c与x轴相交于点B、C(点B在点C左侧),与y轴相交于点A.已知点B坐标为B(1,0),BC=3,△ABC面积为6.
(1)求抛物线的解析式;
(2)如图1,点P为直线AC下方抛物线上一动点,过点P作PD∥AB,交线段AC于点D.求PD长度的最大值及此时P点的坐标;
(3)如图2,将抛物线向左平移个单位长度得到新的抛物线,M为新抛物线对称轴l上一点,N为平面内一点,使得以点A、B、M、N为顶点的四边形为菱形,请直接写出点N的坐标,并写出求解其中一个N点坐标的过程.
8.(2022•恩施市模拟)如图,已知直线y=﹣x﹣3与x轴,y轴分别交于点A,B,抛物线y=x2+bx+c的顶点是(2,﹣1),且与x轴交于C,D两点,与y轴交于点E,P是抛物线上一个动点,过点P作PG⊥AB于点G.
(1)求b、c的值;
(2)若点M是抛物线对称轴上任意点,点N是抛物线上一动点,是否存在点N,使得以点C,D,M,N为顶点的四边形是菱形?若存在,请你求出点N的坐标;若不存在,请你说明理由.
(3)当点P运动到何处时,线段PG的长最小?最小值为多少?
9.(2020秋•沙坪坝区校级期末)如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+2交x轴于点A、B,交y轴于点C.
(1)求△ABC的面积;
(2)如图,过点C作射线CM,交x轴的负半轴于点M,且∠OCM=∠OAC,点P为线段AC上方抛物线上的一点,过点P作AC的垂线交CM于点G,求线段PG的最大值及点P的坐标;
(3)将该抛物线沿射线AC方向平移个单位后得到的新抛物线为y′=ax2+bx+c(a≠0),新抛物线y′与原抛物线的交点为E,点F为新抛物线y′对称轴上的一点,在平面直角坐标系中是否存在点Q,使以点A、E、F、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
10.(2020秋•射阳县期末)已知,如图,抛物线y=ax2+bx+c(a≠0),经过抛物线上的两点A(﹣4,0)和B(2,0),C(0,8),点M是该抛物线顶点.
(1)求抛物线所对应的函数表达式和顶点M坐标;
(2)在抛物线上A、C两点之间的部分(不包含A、C两点),是否存在点D,使的S△DAC=S△MAC?若存在,求出点D的横坐标;若不存在,请说明理由;
(3)若点E是x轴上一个动点,点F为平面直角坐标系内一点,当以点A,C,E,F为顶点的四边形是菱形时,请直接写出满足条件的点E的坐标.
11.(2020•碑林区校级三模)在平面直角坐标系中,抛物线C1:y=﹣x2﹣4x﹣2的顶点为A,与y轴交于点B,将抛物线C1绕着平面内的某一点旋转180°得到抛物线C2,抛物线C2与y轴正半轴相交于点C.
(1)求A、B两点的坐标;
(2)若抛物线C2上存在点D,使得以A、B、C、D四点为顶点的四边形为菱形,请求出此时抛物线C2的表达式.
12.(2022春•兴宁区校级期末)如图,抛物线y=x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,连接AC,BC,点P是直线AC下方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)连接AP,CP,设P点的横坐标为m,△ACP的面积为S,求S与m的函数关系式;
(3)试探究:过点P作BC的平行线1,交线段AC于点D,在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,请直接写出点E的坐标,若不存在,请说明理由.
13.(2020•葫芦岛三模)如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A,B两点,与y轴交于点C,其中A(﹣1,0),B(4,0).
(1)求抛物线的解析式;
(2)连接BC,在直线BC上方的抛物线上有一动点D,连接AD,与直线BC相交于点E,当DE:AE=4:5时,求tan∠DAB的值;
(3)点P是直线BC上一点,在平面内是否存在点Q,使以点P,Q,C,A为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
14.(2020•师宗县一模)如图,直线y=﹣x+3与x轴、y轴分别交于点B,点C,经过B,C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P,点M为抛物线的对称轴上的一个动点.
(1)求该抛物线的解析式;
(2)当点M在x轴的上方时,求四边形COAM周长的最小值;
(3)在平面直角坐标系内是否存在点N,使以C,P,M,N为顶点的四边形为菱形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.
15.(2021•两江新区模拟)如图,抛物线y=ax2+bx+c(a≠0)交x轴于A,B两点,交y轴于点C.其中点A(﹣1,0),B(3,0),C(0,﹣3),连接AC、BC.
(1)求抛物线的解析式;
(2)如图1,在抛物线上B,C两点间有一动点P(点P不与B、C两点重合),过点P作AC的平行线,交BC于点G,求PG的最大值及此时点P的坐标;
(3)如图2,将抛物线y=ax2+bx+c(a≠0)沿射线CB方向平移个单位长度得到新抛物线y′,点M为新抛物线对称轴上的一动点,点N为平面内的任意一点,是否存在点N使得以A,C,M,N为顶点的四边形是以AC为边的菱形,若存在,请直接写出所有符合条件的点N的坐标;若不存在,请说明理由.
16.(2021•淮安区一模)如图1,在平面直角坐标系中,已知矩形ABCD的三个顶点A(﹣3,4)、B(﹣3,0)、C(﹣1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P以每秒1个单位的速度从点D出发,沿DC边向点C运动,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
(1)求该抛物线的解析式;
(2)连接BG,求△BGD的面积最大值;
(3)如图2,在点P运动的同时,点Q从点B出发,沿BA边以每秒1个单位的速度向点A运动.动点P、Q运动的过程中,在矩形ABCD内(包括其边界)是否存在点H,使以B,Q,E,H为顶点的四边形是菱形?若不存在,请说明理由;若存在,请直接写出t的值:t= .
17.(2021•渝中区校级一模)如图,在平面直角坐标系中,已知抛物线y=﹣x2+x+2与x轴相交于A,B两点,与y轴交于点C.
(1)求B、C两点的坐标;
(2)点P为直线BC上方抛物线上的任意一点,过P作PF∥x轴交直线BC于点F,过P作PE∥y轴交直线BC于点E,求线段EF的最大值及此时P点坐标;
(3)将该抛物线沿着射线AC方向平移个单位得到新抛物线y′,N是新抛物线对称轴上一点,在平面直角坐标系中是否存在点Q,使以点B、C、Q、N为顶点的四边形为菱形,若存在,请直接写出点Q点的坐标;若不存在,请说明理由.
18.(2022•岳池县模拟)如图1,一次函数y=x﹣4的图象分别与x轴,y轴交于B,C两点,二次函数y=ax2﹣x+c的图象过B,C两点,且与x轴交于另一点A.
(1)求二次函数的表达式;
(2)点P是二次函数图象的一个动点,设点P的横坐标为m,若∠ABC=2∠ABP.求m的值;
(3)如图2,过点C作CD∥x轴交抛物线于点D.点M是直线BC上一动点,在坐标平面内是否存在点N,使得以点C,D,M,N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
19.(2021•罗湖区校级模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3).且点A的坐标为(﹣1,0),点B的坐标为(3,0),点P是抛物线上第一象限内的一个点.
(1)求抛物线的函数表达式;
(2)连PO、PB,如果把△POB沿OB翻转,所得四边形POP′B恰为菱形,那么在抛物线的对称轴上是否存在点Q,使△QAB与△POB相似?若存在求出点Q的坐标;若不存在,说明理由;
(3)若(2)中点Q存在,指出△QAB与△POB是否位似?若位似,请直接写出其位似中心的坐标.
20.(2021秋•九龙坡区校级月考)如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC,交对称轴于点D.
(1)求抛物线的解析式;
(2)点P是直线BC上方的抛物线上一点,连接PC,PD.求△PCD的面积的最大值以及此时点P的坐标;
(3)将抛物线y=ax2+bx+3向右平移1个单位得到新抛物线,新抛物线与原抛物线交于点E,点F是新抛物线的对称轴上的一点,点G是坐标平面内一点.当以D、E、F、G四点为顶点的四边形是菱形时,直接写出点F的坐标,并写出求解其中一个点F的坐标的过程.
21.(2021•诸城市三模)如图,抛物线y=ax2+bx+4经过点A(﹣2,0),点B(4,0),与y轴交于点C,过点C作直线CD∥x轴,与抛物线交于点D,作直线BC,连接AC.
(1)求抛物线的函数表达式,并用配方法求抛物线的顶点坐标;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上,且位于点C的上方,点N在直线BC上,点P为直线BC上方抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
22.(2021•鞍山一模)如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于A、C两点,抛物线y=﹣x2+bx+c经过A、C两点.
(1)求抛物线的解析式;
(2)点B为y轴上一点,点P为直线AB上一点,过P作PQ∥BC交x轴于点Q,当四边形BCPQ为菱形时,请直接写出B点坐标;
(3)在(2)的条件下,且点B在线段OC上时,将抛物线y=﹣x2+bx+c向上平移m个单位,平移后的抛物线与直线AB交于点D(点D在第二象限),点N为x轴上一点,若∠DNB=90°,且符合条件的点N恰好有2个,求m的取值范围.
23.(2022•巨野县一模)如图,抛物线与x轴交于A(﹣1,0)、B(3,0),交y轴于C(0,3).
(1)求抛物线的解析式;
(2)P是直线BC上方的抛物线上的一个动点,设P的横坐标为t,P到BC的距离为h,求h与t的函数关系式,并求出h的最大值;
(3)设点M是x轴上的动点,在平面直角坐标系中,存在点N,使得以点A、C、M、N为顶点的四边形是菱形,直接写出所有符合条件的点N坐标.
24.(2021•洛阳一模)如图,直线y=x﹣3与x轴、y轴分别交于B、C两点,抛物线y=x2+bx+c经过B、C,且与x轴另一交点为A,连接AC.
(1)求抛物线的解析式;
(2)点E在抛物线上,连接EC,当∠ECB+∠ACO=45°时,求点E的横坐标;
(3)点M从点A出发,沿线段AB由A向B运动,同时点N从点C出发沿线段CA由C向A运动,M,N的运动速度都是每秒1个单位长度,当N点到达A点时,M,N同时停止运动,问在坐标平面内是否存在点D,使M,N运动过程中的某些时刻t,以A,D,M,N为顶点的四边形为菱形?若存在,直接写出t的值;若不存在,说明理由.
25.(2021•山西模拟)综合与探究.
如图,抛物线y=﹣x2+x+与x轴交于A,B两点(点A在点B的左侧),顶点为D.点P为对称轴右侧抛物线上的一个动点,其横坐标为m,直线AD交y轴于点C,过点P作PF∥AD,交x轴于点F,PE∥x轴,交直线AD于点E,交直线DF于点M.
(1)求直线AD的表达式及点C的坐标;
(2)当四边形AFPE的面积与△ADF的面积相等时,求m的值;
(3)试探究点P在运动过程中,是否存在m,使四边形AFPE是菱形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
26.(2021•交城县二模)实践与探究
如图1,已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线的解析式;
(2)P(x,y)是抛物线上的一点,若△ADP与△ADC的面积相等,求出所有符合条件的点P的坐标.
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.
专题8二次函数与矩形存在性问题(学生版)-拔尖2023中考数学压轴题突破(全国通用): 这是一份专题8二次函数与矩形存在性问题(学生版)-拔尖2023中考数学压轴题突破(全国通用),共15页。试卷主要包含了矩形的判定,题型分析等内容,欢迎下载使用。
专题7二次函数与菱形存在性问题(教师版)-拔尖2023中考数学压轴题突破(全国通用): 这是一份专题7二次函数与菱形存在性问题(教师版)-拔尖2023中考数学压轴题突破(全国通用),共97页。
专题6二次函数与平行四边形存在性问题(教师版)-拔尖2023中考数学压轴题突破(全国通用): 这是一份专题6二次函数与平行四边形存在性问题(教师版)-拔尖2023中考数学压轴题突破(全国通用),共70页。












