
2024年陕西省西安市高新唐南中学中考五模数学试题(无答案)
展开一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.下列实数中,无理数的是( )
A.B.C.D.
2.下列图形中,是中心对称但不是轴对称图形的是( )
A.B.C.D.
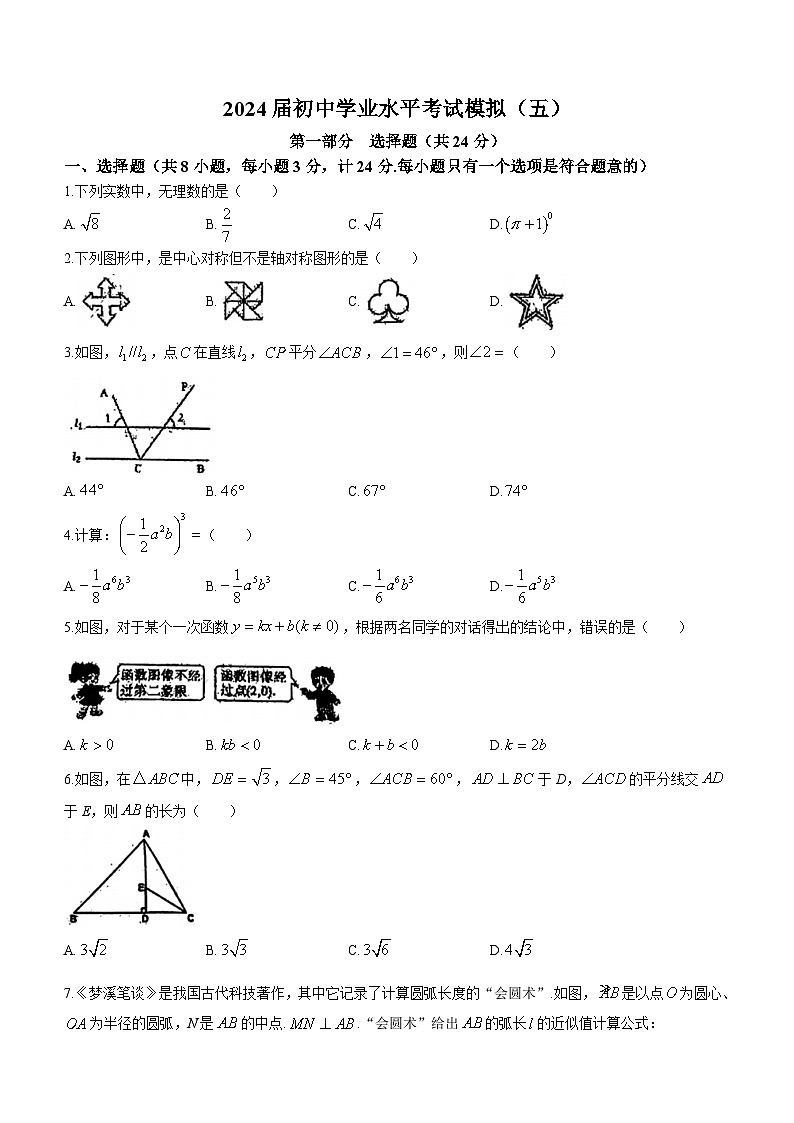
3.如图,,点在直线,平分,,则( )
A.B.C.D.
4.计算:( )
A.B.C.D.
5.如图,对于某个一次函数,根据两名同学的对话得出的结论中,错误的是( )
A.B.C.D.
6.如图,在中,,,,于D,的平分线交于E,则的长为( )
A.B.C.D.
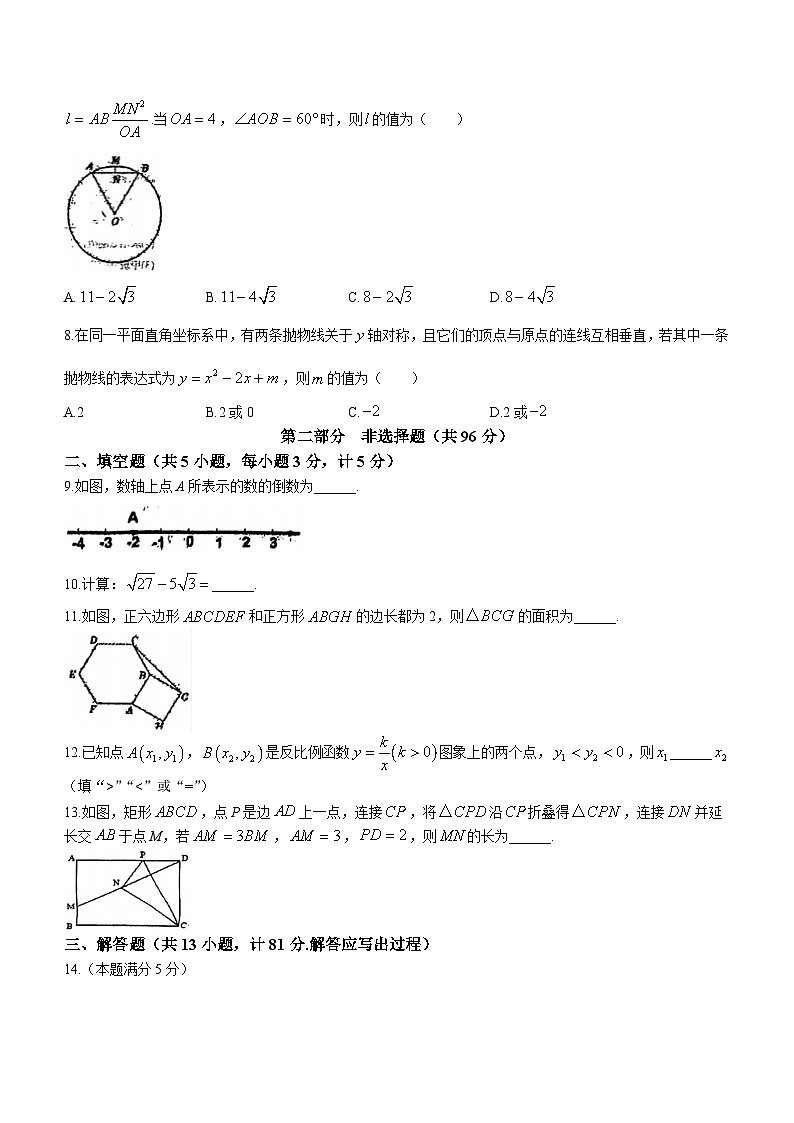
7.《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,是以点为圆心、为半径的圆弧,N是的中点..“会圆术”给出的弧长的近似值计算公式:.当,时,则的值为( )
A.B.C.D.
8.在同一平面直角坐标系中,有两条抛物线关于轴对称,且它们的顶点与原点的连线互相垂直,若其中一条抛物线的表达式为,则的值为( )
A.2B.2或0C.D.2或
第二部分 非选择题(共96分)
二、填空题(共5小题,每小题3分,计5分)
9.如图,数轴上点A所表示的数的倒数为______.
10.计算:______.
11.如图,正六边形和正方形的边长都为2,则的面积为______.
12.已知点,是反比例函数图象上的两个点,,则______(填“>”“<”或“=”)
13.如图,矩形,点P是边上一点,连接,将沿折叠得,连接并延长交于点M,若,,,则的长为______.
三、解答题(共13小题,计81分.解答应写出过程)
14.(本题满分5分)
计算:
15.(本题满分5分)
解方程:
16.(本题满分5分)
解不等式:,并写出最大整数解.
17.(本题满分5分)
如图,在中,,.请用尺规作图法,在线段上求作一点P,使得.(保留作图痕迹,不写作法)
18.(本题满分5分)
如图,在中,,点D在边上,且,过点D作交于点F,连接,且,求证:.
19.(本题满分5分)
《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱,问合伙人数是多少?
20.(本题满分5分)
为了弘扬雷锋精神,某校组织“学雷锋,争做新时代好少年”的宣传活动,根据活动要求,每班需要2名宣传员,某班班主任决定从甲、乙、丙、丁4名同学中随机选取2名同学作为宣传员.
(1)“甲、乙同学都被选为宣传员”是______事件;(填“必然”、“不可能”或“随机”)
(2)请用画树状图法或列表法,求甲、丁同学都被选为宣传员的概率.
21.(本题满分6分)
(科技成就)随着技术的发展,为扩大网络信号的辐射范围,某通信公司在一座坡度为的小山坡上新建了一座大型的网络信号发射塔(如图所示),信号塔底端Q到坡底A的距离为3.9米.同时为了提醒市民,在距离斜坡底A点4.4米的水平地面上立了一块警示牌,当太阳光线与水平线成角时,测得信号塔落在警示牌上的影子长为3米.求信号塔的高.(结果精确到0.1米,参考数据:,,)
22.(本题满分7分)
某校甲乙两班联合举办了“经典阅读”竞赛,从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩,并对数据(成绩)进行了收集、整理,分析.下面给出了部分信息.
【收集数据】
甲班10名学中竞赛成绩:
70,71,72,78,79,79,85,86,89,91
乙班10名学生竞赛成绩:
73,74,75,77,80,80,81,85,85,90
【分析数据】
【解决问题】
根据以上信息,回答下列问题:
(1)填空:______,______;
(2)求出的值,并说明哪个班的成绩更稳定;
(3)甲班共有学生45人,乙班其有学生40人.按竞赛规定,80分及80分以上的学生可以获奖,估计这两个班可以获奖的总人数是多少?
23.(本题满分7分)
某食用油的沸点温度远高于水的沸点温度,小聪想用刻度不超过的温度计测算出这种食用油沸点的温度.在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔测量一次锅中油温,得到的数据记录如下:
(1)小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温(单位:)与加热的时间(单位:)符合初中学习过的某种函数关系,填空:可能是______函数关系(请选填“正比例”“一次”“二次”“反比例”);
(2)根据以上判断,求关于的函数解析式;
(3)当加热时,油沸腾了,请推算沸点的温度.
24.(本题满分8分)
如图,为的直径,为上一点,连接,,过点作的切线交延长线于点.
(1)求证:;
(2)若,,求的半径.
25.(本题满分8分)
在平面直角坐标系中,抛物线:与轴交于,两点,与轴的交点为.
(1)求抛物线的函数表达式;
(2)将抛物线向右平移2个单位长度得到抛物线,已知点为抛物线对称轴上一点,点为抛物线上一点,是否存在以A,C,P,D为顶点且以为边的四边形为平行四边形?若存在,求出所有满足条件的点的坐标,若不存在,请说明理由.
26.(本题满分10分)
问题探究
(1)如图,已知,,,求面积的最大值.
问题解决
(2)为美化环境,我市园林设计部门准备在人民广场用鲜花拼成一个平行四边形的花卉展览场地供市民观赏.如图所示,在平行四边形中,点为边上一点且,,米.为了种植更多的鲜花,要求平行四边形的面积尽可能大.请问平行四边形面积是否存在最大值?如果存在,请计算平行四边形面积的最大值;如果不存在,请说明理由.
班级
平均数
中位数
众数
方差
甲班
80
51.4
乙班
80
80
80,85
时间
0
10
20
30
40
油温
10
30
50
70
90
2023年陕西省西安市雁塔区高新唐南中学中考数学五模试卷(含解析): 这是一份2023年陕西省西安市雁塔区高新唐南中学中考数学五模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年陕西省西安高新唐南中学中考五模数学试题: 这是一份2023年陕西省西安高新唐南中学中考五模数学试题,共7页。
2023年陕西省西安市雁塔区高新唐南中学中考数学五模试卷(含解析): 这是一份2023年陕西省西安市雁塔区高新唐南中学中考数学五模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












