广东省深圳市深圳外国语学校2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份广东省深圳市深圳外国语学校2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含广东省深圳市深圳外国语学校2023-2024学年七年级下学期期中数学试题原卷版docx、广东省深圳市深圳外国语学校2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

一、选择题（共10题，每题3分，共30分）
1. 下列各式的计算中，正确的是（ ）
A B.
C. D.
【答案】D
【解析】
【分析】根据单项式的除法、合并同类项的法则、完全平方公式和同底数幂的乘法法则逐项判断即得答案．
【详解】解：A、，故此选项计算错误；
B、，无法合并，故此选项计算错误；
C、，故此选项计算错误；
D、，故本选项计算正确；
故选：D．
【点睛】本题考查单项式的除法、完全平方公式和同底数幂的乘法等知识，熟练掌握整式的运算法则是解题的关键．
2. 下列事件中是必然事件的是（ ）
A. 打开电视机，正在播放《开学第一课》B. 经过有交通信号灯的路口，遇到红灯
C. 任意画一个三角形，其内角和是D. 买一张彩票，一定不会中奖
【答案】C
【解析】
【分析】本题考查事件的分类，根据必然事件是一定条件，一定会发生的事件，进行判断即可．
【详解】解：A、打开电视机，正在播放《开学第一课》，是随机事件，不符合题意；
B、经过有交通信号灯的路口，遇到红灯，是随机事件，不符合题意；
C、任意画一个三角形，其内角和是，是必然事件，符合题意；
D、买一张彩票，一定不会中奖，是随机事件，不符合题意；
故选C．
3. “白日不到处，青春恰自来．苔花如米小，也学牡丹开．”这是清朝袁枚所写五言绝句《苔》，这首咏物诗启示我们身处逆境也要努力绽放自己，要和苔花一样尽自己所能实现人生价值．苔花也被称为“坚韧之花”．袁枚所写的“苔花”很可能是苔类孢子体的苞荫，某孢子体的苞荫直径约为0.0000084m，将数据0.0000084用科学记数法表示为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查科学记数法，根据科学记数法的表示方法求解即可．科学记数法的表示形式为的形式，其中，n为整数．解题关键是正确确定a的值以及n的值．
【详解】0.0000084用科学记数法表示为．
故选：B．
4. 如图，把一个含角的直角三角尺的一个顶点放在直尺的一边上，若，则的度数为（ ）

A. B. C. D.
【答案】D
【解析】
【分析】本题考查了平行线的性质，直角三角形两锐角互余，由可得，由直角三角形两锐角互余可得，据此即可求解，掌握平行线和直角三角形的性质是解题的关键．
【详解】解：如图，

∵，
∴，
∵，
∴，
故选：．
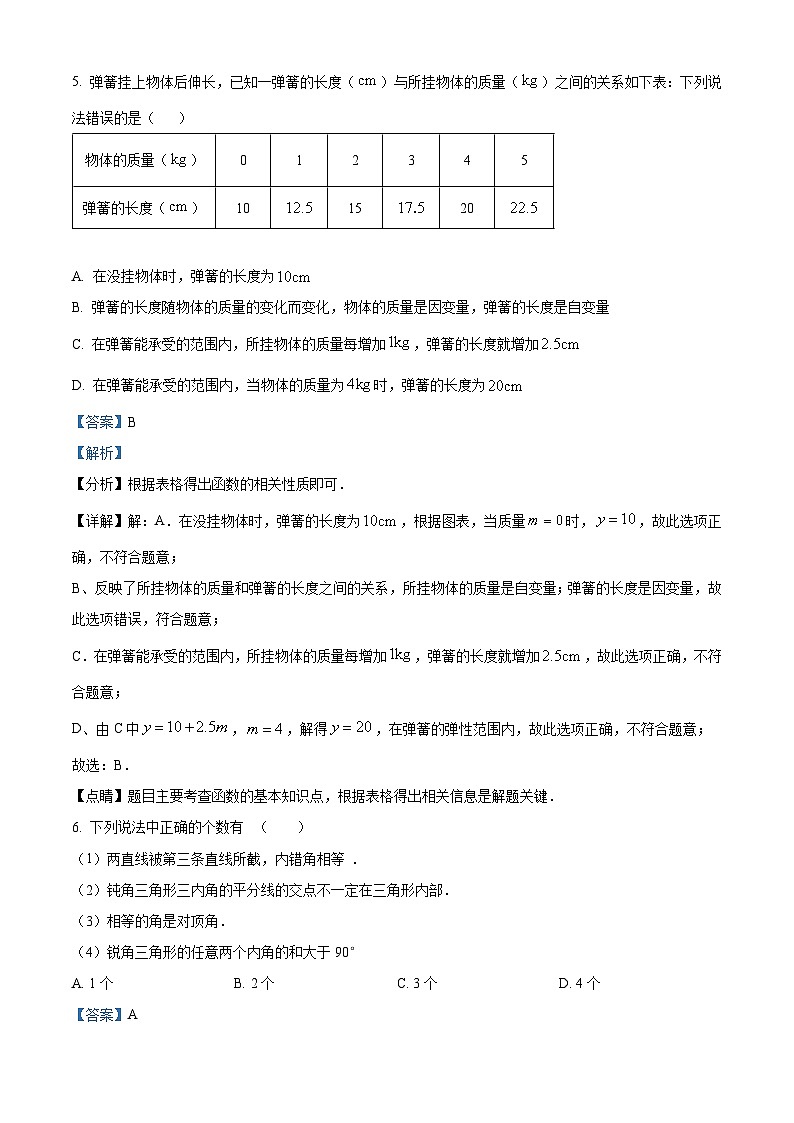
5. 弹簧挂上物体后伸长，已知一弹簧的长度（）与所挂物体的质量（）之间的关系如下表：下列说法错误的是（ ）
A. 在没挂物体时，弹簧的长度为
B. 弹簧的长度随物体的质量的变化而变化，物体的质量是因变量，弹簧的长度是自变量
C. 在弹簧能承受的范围内，所挂物体的质量每增加，弹簧的长度就增加
D. 在弹簧能承受的范围内，当物体的质量为时，弹簧的长度为
【答案】B
【解析】
【分析】根据表格得出函数的相关性质即可．
【详解】解：A．在没挂物体时，弹簧的长度为，根据图表，当质量时，，故此选项正确，不符合题意；
B、反映了所挂物体的质量和弹簧的长度之间的关系，所挂物体的质量是自变量；弹簧的长度是因变量，故此选项错误，符合题意；
C．在弹簧能承受的范围内，所挂物体的质量每增加，弹簧的长度就增加，故此选项正确，不符合题意；
D、由C中，，解得，在弹簧的弹性范围内，故此选项正确，不符合题意；
故选：B．
【点睛】题目主要考查函数的基本知识点，根据表格得出相关信息是解题关键．
6. 下列说法中正确的个数有 （ ）
（1）两直线被第三条直线所截，内错角相等 ．
（2）钝角三角形三内角的平分线的交点不一定在三角形内部．
（3）相等的角是对顶角．
（4）锐角三角形的任意两个内角的和大于90°
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】根据平行线的性质，三角形的角平分线的定义，对顶角的定义，三角形内角和定理，逐项分析判断即可求解．
【详解】（1）两平行直线被第三条直线所截，内错角相等，故该说法不正确，
（2）钝角三角形三内角的平分线的交点一定在三角形内部，故该说法不正确，
（3）相等的角不一定是对顶角，故该说法不正确，
（4）锐角三角形的任意两个内角的和大于，故该说法正确，
故选A．
【点睛】本题考查了平行线的性质，三角形的角平分线的定义，对顶角的定义，三角形内角和定理，掌握以上知识是解题的关键．
7. 如图，在中，，．按以下步骤尺规作图：①以点为圆心，任意长为半径画弧，分别交和的延长线于点，．②分别以，为圆心，同样的长为半径画弧，两弧交于点．③做射线．则的度数为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了作角平分线以及三角形的外角性质，掌握基本作图是解题的关键．根据三角形的外角性质可得，由作图方法可得是的角平分线，从而即可求解．
【详解】解：∵，
∴，
∵是的角平分线，
∴，
故选：A．
8. 如图，在长方形ABCD中，动点P从A出发，以一定的速度，沿方向运动到点A处停止（提示：当点P在AB上运动时，点P到DC的距离始终等于AD和BC）．设点P运动的路程为x，的面积为y，如果y与x之间的关系如图所示，那么长方形ABCD的面积为（ ）
A 6B. 9C. 15D. 18
【答案】D
【解析】
【分析】根据题意结合图象得出AB、BC的长度，再求出面积即可．
【详解】由题意可知，当点P从点A运动到点B时，△PCD的面积为：，即△PCD的面积不变，则结合图象可知AB=6，
当点P从点B运动到点C时，△PCD的面积逐渐变小直到为0，
即结合图象可知BC=x-AB=9-6=3，
∴长方形ABCD面积为：AB•BC=6×3=18．
故选：D．
【点睛】本题考查了动点问题的函数图象，能根据图形得出正确信息是解此题的关键．
9. 小丽与爸爸、妈妈在公园里荡秋千，如图，小丽坐在秋千的起始位置处，与地面垂直，小丽两脚在地面上用力一蹬，妈妈在处接住她后用力一推，爸爸在处接住她．若点距离地面的高度为，点到的距离为，点距离地面的高度是，，则点到的距离为( )
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了全等三角形的判定与性质的应用，由证明得出，即可推出结果．
【详解】解：点距离地面的高度为，点距离地面的高度是，
点距离地面的高度为，点距离地面的高度是，
，
，
，
，
又由题意可知，，
，
，，
，
点到的距离为，
故选：D．
10. 如图，在中，，平分交于点平分交于点交于点．则下列说法正确的个数为（ ）
①；②，③若，则；④；⑤．
A. 2个B. 3个C. 4个D. 5个
【答案】C
【解析】
【分析】①根据三角形内角和定理可得可得，然后根据平分平分，可得，，再根据三角形内角和定理即可进行判断；
②当是的中线时，，进而可以进行判断；
③根据，证明为等边三角形，根据三线合一的性质进而可以进行判断；
④作的平分线交于点，可得，证明，，可得，进而可以判断；
⑤过作于点，由④知，为的角平分线，可得，所以可得，根据，进而可以进行判断．
【详解】解：①在中，，
∴，
∵平分平分，
∴，，
∴，故①正确；
②当是的中线时，，故②错误；
③∵，
∴为的中线，
∵为的角平分线，
∴，
∴为等边三角形，
∴，故③正确；
④如图，作的平分线交于点，
由①得，
∴，
∴，
∴，
∵，
∴，
∴，
∴，故④正确；
⑤过作，于点，
由④知，为的角平分线，
∴，
∴，
∵，
∴，故⑤正确．
综上所述：正确的有①③④⑤，共4个，
故选：C．
【点睛】本题考查了角平分线的定义以及性质，等边三角形的性质，等腰三角形的性质与判定，三角形全等的性质和判定，作辅助线，构建三角形全等是解题关键．
二、填空题（共5题，每题3分，共15分）
11. 如图所示的计算程序中，y与x之间的关系式是______________．
【答案】
【解析】
【分析】根据程序框图列出正确的关系式即可得解．
【详解】解：根据程序框图可得 ；
故答案为：．
【点睛】本题考查根据程序框图列关系式，解题的关键是按照运算顺序准确列出关系式．
12. 已知是一个完全平方式，则m的值是：_________．
【答案】4
【解析】
【分析】本题考查了对完全平方公式的应用，注意：完全平方式有两个，是和．根据完全平方式得出，即可求出答案．
【详解】解：∵是一个完全平方式，
∴，
，
故答案为：4．
13. 如图，∠1=∠2，要利用“SAS”说明△ABD≌△ACD，需添加的条件是_________．
【答案】BD=CD
【解析】
【详解】BD=CD，
理由是：，
∵在△ABD和△ACD中
∴△ABD≌△ACD（SAS），
故答案为BD=CD．
14. 如图，在中，边上的高，点E为上的点，且，若，则图中阴影部分面积为________．
【答案】
【解析】
【分析】此题考查了等腰直角三角形的判定和性质、三角形的面积、平方差公式等知识，求出是解题的关键．证明是等腰直角三角形，得到，证明是等腰直角三角形，得到，推导出，即可得到答案．
【详解】解：∵边上的高，
∴，是等腰直角三角形，
∴，
∵，
∴是等腰直角三角形，
∴，
∵，
∴
，
∴，
即图中阴影部分面积为．
故答案为：20．
15. 如图，点在线段上，于，于．，且，，点以的速度沿向终点运动，同时点以的速度从开始，在线段上往返运动（即沿运动），当点到达终点时，，同时停止运动．过，分别作的垂线，垂足为，．设运动时间为s，当以，，为顶点的三角形与全等时，的值为__________．
【答案】1或
【解析】
【分析】本题主要考查全等三角形的性质，以，，为顶点的三角形与全等时，，分点沿运动和沿运动两种情况，根据列方程，即可求解．注意分情况讨论是解题的关键．
【详解】解：点P从运动到点C从用时间为：，
点从运动到点C从用时间为：，
点从运动到点C后，从点C返回，又运动了．
如图，
以，，为顶点的三角形与全等，
，
当点沿运动时，，
解得；
当点沿运动时，，
解得，，符合题意，
综上所述，的值为1或．
故答案为：1或．
三、解答题（共7题，共55分）
16. （1）计算：；
（2）先化简，再求值：，其中，．
【答案】（1）25；（2），
【解析】
【详解】本题考查了整式的运算，解题的关键是：
（1）把变形为，然后利用平方差公式计算即可；
（2）原式先利用完全平方公式、单项式乘多项式、平方差公式展开，再合并同类项即可化简，最后把、的值代入计算可得．
【解答】（1）解：原式
；
（2）解：原式
．
当、时，
原式
．
17. 如图反映的是小华从家里跑步去体育馆，在那里锻炼了一段时间后又走到文具店去买笔，然后散步回家，其中（分）表示时间，（千米）表示小华离家的距离．根据图象回答下列问题：
（1）体育馆距离小华家__________千米，小华在体育馆锻炼了__________分钟；
（2）体育馆距离文具店__________千米，小华在文具店买笔用了__________分钟；
（3）小华从家跑步到体育馆，从文具店散步回家的速度分别是多少千米/小时？
【答案】（1）2.5；15
（2）1；20 （3）小华从家跑步到体育场的速度为10千米/小时；小华从文具店散步回家的速度为千米/小时
【解析】
【分析】本题考查了函数图象，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．需注意计算单位的统一．
（1）根据观察函数图象的纵坐标，可得距离，观察函数图象的横坐标，可得时间；
（2）根据观察函数图象的横坐标，可得体育馆与文具店的距离，观察函数图象的横坐标，可得在文具店停留的时间；
（3）根据观察函数图象的纵坐标，可得路程，根据观察函数图象的横坐标，可得回家的时间，根据路程与时间的关系，可得答案．
小问1详解】
解：（1）由纵坐标看出体育馆距离小华家2.5千米，由横坐标看出小华在体育馆锻炼了15分钟；
故答案为：2.5；15．
【小问2详解】
解：由纵坐标看出体育馆距离文具店（千米），由横坐标看出小华在文具店买笔用了（分）．
故答案为：1；20．
【小问3详解】
解：小华从家跑步到体育馆的速度为（千米小时），
小华从文具店散步回家的平均速度是（千米/小时）．
答：小华从家跑步到体育场的速度为10千米/小时；小华从文具店散步回家的速度为千米/小时．
18. 如图，、在上，且，，，求证：与互相平分，且．补全下面的解题过程：
证明：，
__________＝__________，即，
在和中，
（__________________），
．
（__________________）．
在和中，
（__________________），
，，即与互相平分．
【答案】见解析
【解析】
【分析】本题考查了全等三角形判定和性质．先证得，再证，根据全等三角形的性质即可证明与互相平分．
【详解】证明：，
即，
在和中，
，
，
．
在和中，
，
，，
即与互相平分．
19. 在一个不透明的口袋中装有白、红、黑三种颜色的小球，其中白球3个，红球3个，黑球2个，它们除了颜色外其他都相同．
（1）从袋中随机摸出1个球，求摸出白球的概率．
（2）从袋中随机摸出1个球，求摸出黑球的概率．
（3）向袋中加几个黑球，可以使摸出红球的概率变为?
【答案】（1）
（2）
（3）4
【解析】
【分析】（1）根据概率公式计算，即可得到答案；
（2）根据概率公式计算，即可得到答案；
（3）设向袋中加黑球的数量为，结合概率的性质，通过求解分式方程，即可得到答案．
【小问1详解】
解：根据题意，小球共8只，
从袋中随机地摸出1只球，共8种情况，
白球3只，
从袋中随机地摸出1只球，摸出白球的概率；
【小问2详解】
结合（1）的结论，得：从袋中随机地摸出1只球，共8种情况，
黑球2只，
从袋中随机地摸出1只球，摸出黑球的概率；
【小问3详解】
设向袋中加黑球的数量为，
从袋中随机地摸出1只球，共种情况，
摸出红球的概率为，且红球3只，
，
，
时，，
是方程的解，
向袋中加4只黑球，可以使摸出红球的概率变为．
【点睛】本题考查了概率公式，解题的关键是熟练掌握概率和分式方程的性质，从而完成求解．
20. 如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O
（1）求证：△AEC≌△BED；
（2）若∠1＝38°，求∠BDE的度数．
【答案】（1）见解析；（2）71°．
【解析】
【分析】（1）根据全等三角形的判定即可判断△AEC≌△BED；
（2）由（1）可知：EC=ED，∠C=∠BDE，根据等腰三角形的性质即可知∠C的度数，从而可求出∠BDE的度数；
【详解】（1）证明：∵AE和BD相交于点O，
∴∠AOD=∠BOE．
在△AOD和△BOE中，
∠A=∠B，∴∠BEO=∠2．
又∵∠1=∠2，
∴∠1=∠BEO，
∴∠AEC=∠BED．
在△AEC和△BED中，
，
∴△AEC≌△BED（ASA）．
（2）∵△AEC≌△BED，
∴EC=ED，∠C=∠BDE．
在△EDC中，
∵EC=ED，∠1=38°，
∴∠C=∠EDC=71°，
∴∠BDE=∠C=71°．
【点睛】此题考查全等三角形，解题的关键是熟练运用全等三角形的性质与判定，本题属于中等题型．
21. 阅读下列材料，解决相应问题：
（1）36和84______“友好数对”．（填“是”或“不是”）
（2）为探究“友好数对”的本质，可设“友好数对”中一个数的十位数字为，个位数字为，且；另一个数的十位数字为，个位数字为，且，则，，，之间存在一个等量关系，其探究和说理过程如下，请你将其补充完整．
解：根据题意，“友好数对”中的两个数分别表示为和，将它们各自的十位数字和个位数字交换位置后两个数依次表示为__________和____________．
因为它们是友好数对，所以______________________．
并试求，，，的等量关系．
（3）若有一个两位数，十位数字为，个位数字为，另一个两位数，十位数字为，个位数字为且这两个数为“友好数对”，直接写出这两个两位数．
【答案】（1）是 （2），，，
（3）31和39
【解析】
【分析】（1）计算和，根据定义判断；
（2）利用“十位数字个位数字”表达出交换后的两位数，结合友好数对的定义列出等量关系，并化简；
（3）根据（2）得，解方程得到，写出两个两位数．
【小问1详解】
解：∵，，
∴，
∴36和84是友好数对．
【小问2详解】
解：，，，
∵这两个数是友好数对，
∴，
化简得：．
【小问3详解】
解：由（2）得：，
解得：，
∴两个两位数为：31和39．
【点睛】本题考查了新定义，对于数的表示、整式的运算——多项式乘多项式、解一元一次方程，理解新定义列出方程是关键．
22. 在学习全等三角形知识时，数学兴趣小组发现这样一个模型：模型是由两个顶角相等且有公共顶角顶点的等腰三角形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．这个数学兴趣小组进行了如下操作：
（1）如图1，在和中，，，，连接，，当点落在边上，且，，三点共线时，则在这个“手拉手模型”中，和全等的三角形是____________，的度数为____________．
（2）如图2，已知，分别以、为直角边向两侧作等腰直角和等腰直角，其中，连接、，线段和交于点．
①证明：且；
②若与在同一直线上，如图3，延长与交于点，连接并延长，的延长线与边交于点，且，若和的面积之和为20，的面积为6，求线段的长．
【答案】（1），；
（2）①证明见解析；②4
【解析】
【分析】（1）利用证明，得出，结合三角形外角的性质即可得出，即可求解；
（2）①利用证明，得出，，然后利用三角形外角的性质即可得出；
②利用①中，得出，则可求，利用等角对等边得出，可得出，由的面积可求，由和的面积之和为20，可求，利用完全平方公式变形求出，，求出、，进而求出，即可求解．
【小问1详解】
解：如图1中，
在和中，
，
，
，
，
故答案为：，；
【小问2详解】
解：①和均为等腰直角三角形，，
，，
，
，
在和中，
，
，，
，
；
②和的面积之和为20，和均为等腰直角三角形，
，，，，，
，
，
，
，
，
，
，
，
，
的面积为6，，
，即，
，
，
，
，
，
，
，
，
，
，
，，
，，
．
【点睛】本题考查了全等三角形的判定与性质，三角形外角的性质，等腰直角三角形的性质等知识，明确题意，寻找出全等三角形是解题的关键．
物体的质量（）
0
1
2
3
4
5
弹簧的长度（）
10
15
20
“友好数对”
已知两个两位数，将它们各自的十位数字和个位数字交换位置后，得到两个与原
两个两位数均不同的新数，若这两个两位数的乘积与交换位置后两个新两位数的乘积
相等，则称这样的两个两位数为“友好数对”例如，所以
和与和都是“友好数对”．