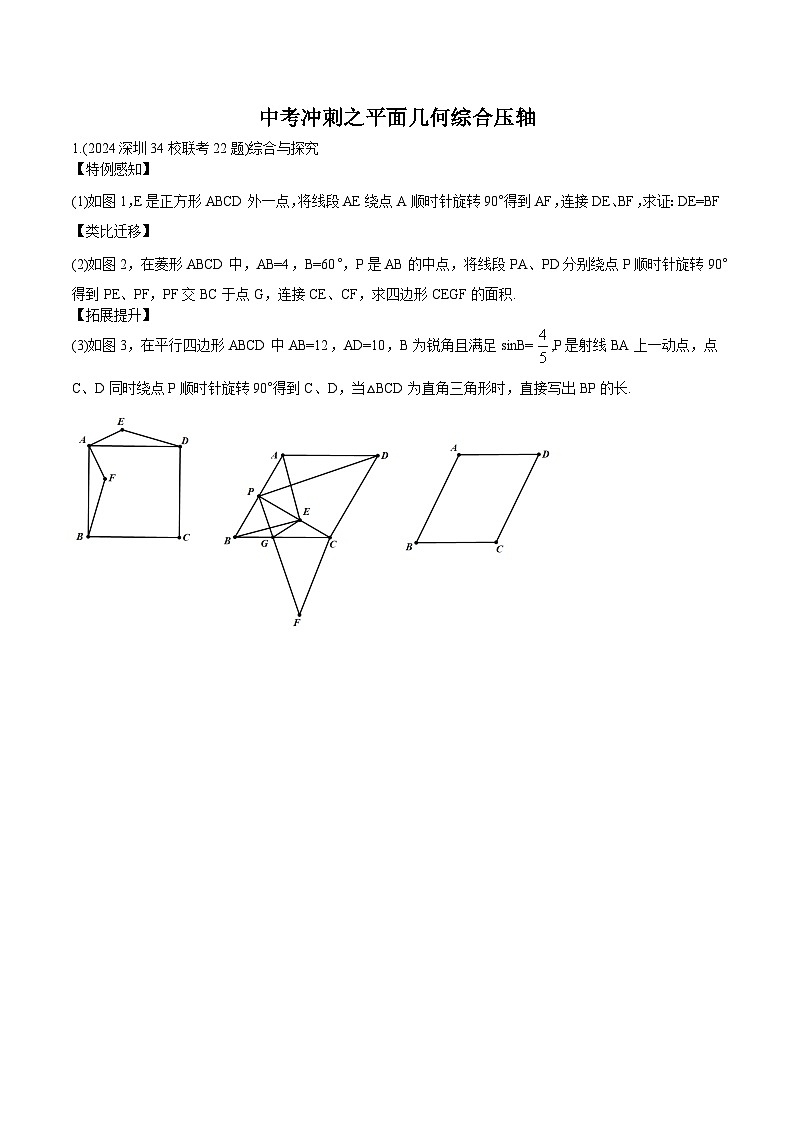
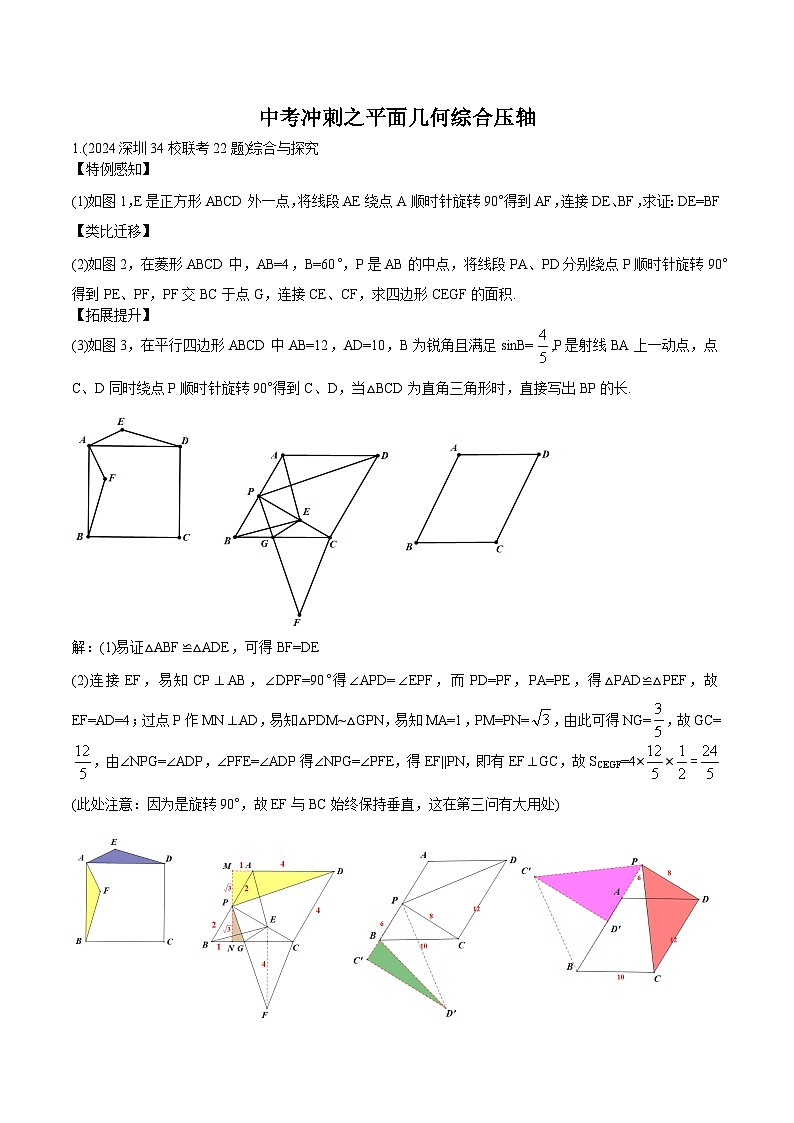
中考冲刺之平面几何综合压轴

这是一份中考冲刺之平面几何综合压轴，文件包含中考冲刺之平面几何综合压轴-教师版docx、中考冲刺之平面几何综合压轴-学生版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

【特例感知】
(1)如图1，E是正方形ABCD外一点，将线段AE绕点A顺时针旋转90°得到AF，连接DE、BF，求证：DE=BF
【类比迁移】
(2)如图2，在菱形ABCD中，AB=4，B=60°，P是AB的中点，将线段PA、PD分别绕点P顺时针旋转90°得到PE、PF，PF交BC于点G，连接CE、CF，求四边形CEGF的面积.
【拓展提升】
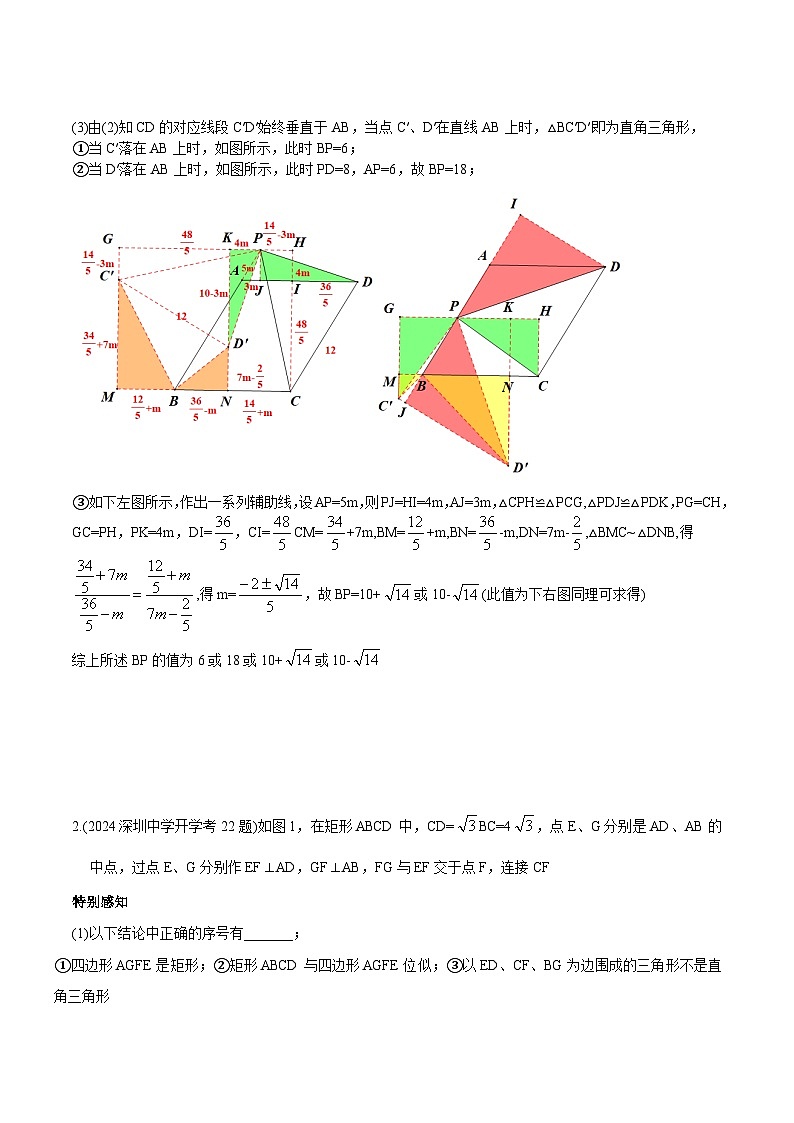
(3)如图3，在平行四边形ABCD中AB=12，AD=10，B为锐角且满足sinB=,P是射线BA上一动点，点C、D同时绕点P顺时针旋转90°得到C、D，当△BCD为直角三角形时，直接写出BP的长.
解：(1)易证△ABF≌△ADE，可得BF=DE
(2)连接EF，易知CP⊥AB，∠DPF=90°得∠APD=∠EPF，而PD=PF，PA=PE，得△PAD≌△PEF，故EF=AD=4；过点P作MN⊥AD，易知△PDM~△GPN，易知MA=1，PM=PN=，由此可得NG=，故GC=，由∠NPG=∠ADP，∠PFE=∠ADP得∠NPG=∠PFE，得EF||PN，即有EF⊥GC，故SCEGF=4××=(此处注意：因为是旋转90°，故EF与BC始终保持垂直，这在第三问有大用处)
(3)由(2)知CD的对应线段C′D′始终垂直于AB，当点C′、D′在直线AB上时，△BC′D′即为直角三角形，
①当C′落在AB上时，如图所示，此时BP=6；
②当D′落在AB上时，如图所示，此时PD=8，AP=6，故BP=18；
③如下左图所示，作出一系列辅助线，设AP=5m，则PJ=HI=4m，AJ=3m，△CPH≌△PCG,△PDJ≌△PDK，PG=CH，GC=PH，PK=4m，DI=，CI=CM=+7m,BM=+m,BN=-m,DN=7m-,△BMC~△DNB,得,得m=，故BP=10+或10-(此值为下右图同理可求得)
综上所述BP的值为6或18或10+或10-
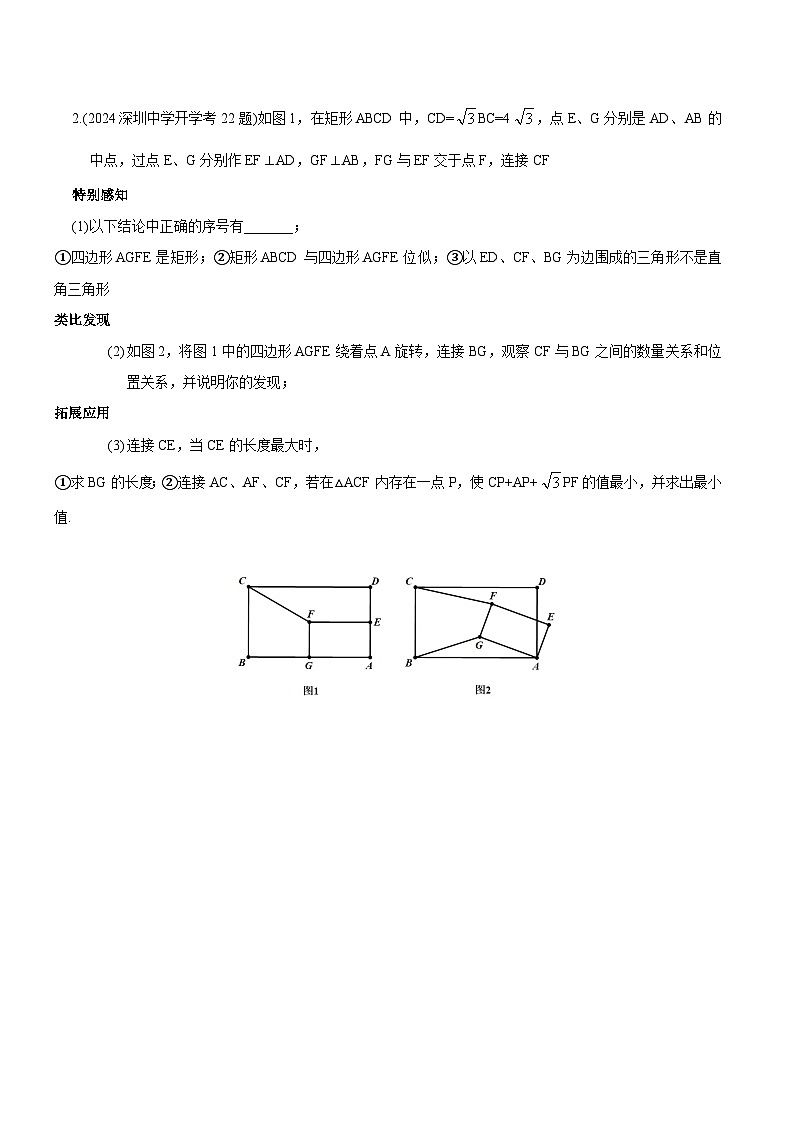
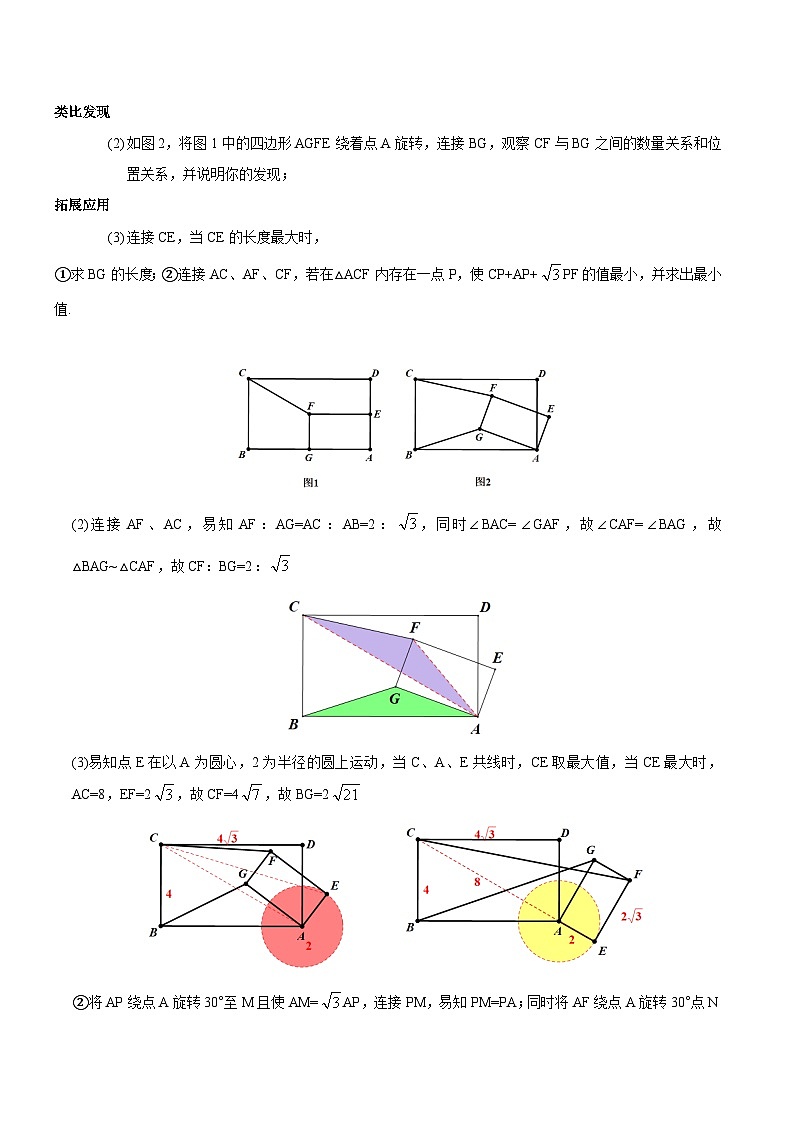
2.(2024深圳中学开学考22题)如图1，在矩形ABCD中，CD=BC=4，点E、G分别是AD、AB的中点，过点E、G分别作EF⊥AD，GF⊥AB，FG与EF交于点F，连接CF
特别感知
以下结论中正确的序号有_______；
①四边形AGFE是矩形；②矩形ABCD与四边形AGFE位似；③以ED、CF、BG为边围成的三角形不是直角三角形
类比发现
如图2，将图1中的四边形AGFE绕着点A旋转，连接BG，观察CF与BG之间的数量关系和位置关系，并说明你的发现；
拓展应用
连接CE，当CE的长度最大时，
①求BG的长度；②连接AC、AF、CF，若在△ACF内存在一点P，使CP+AP+PF的值最小，并求出最小值.
(2)连接AF、AC，易知AF：AG=AC：AB=2：，同时∠BAC=∠GAF，故∠CAF=∠BAG，故△BAG~△CAF，故CF：BG=2：
(3)易知点E在以A为圆心，2为半径的圆上运动，当C、A、E共线时，CE取最大值，当CE最大时，AC=8，EF=2，故CF=4，故BG=2
②将AP绕点A旋转30°至M且使AM=AP，连接PM，易知PM=PA；同时将AF绕点A旋转30°点N且使AN=AM，易得△APF~△AMN，得NM=PF，故PA+PC+PF=PC+PM+MN，当C、P、M、N共线时，故最小值，即CN，此时∠CAN=150°，AN=4，CN=4，故最小值为4
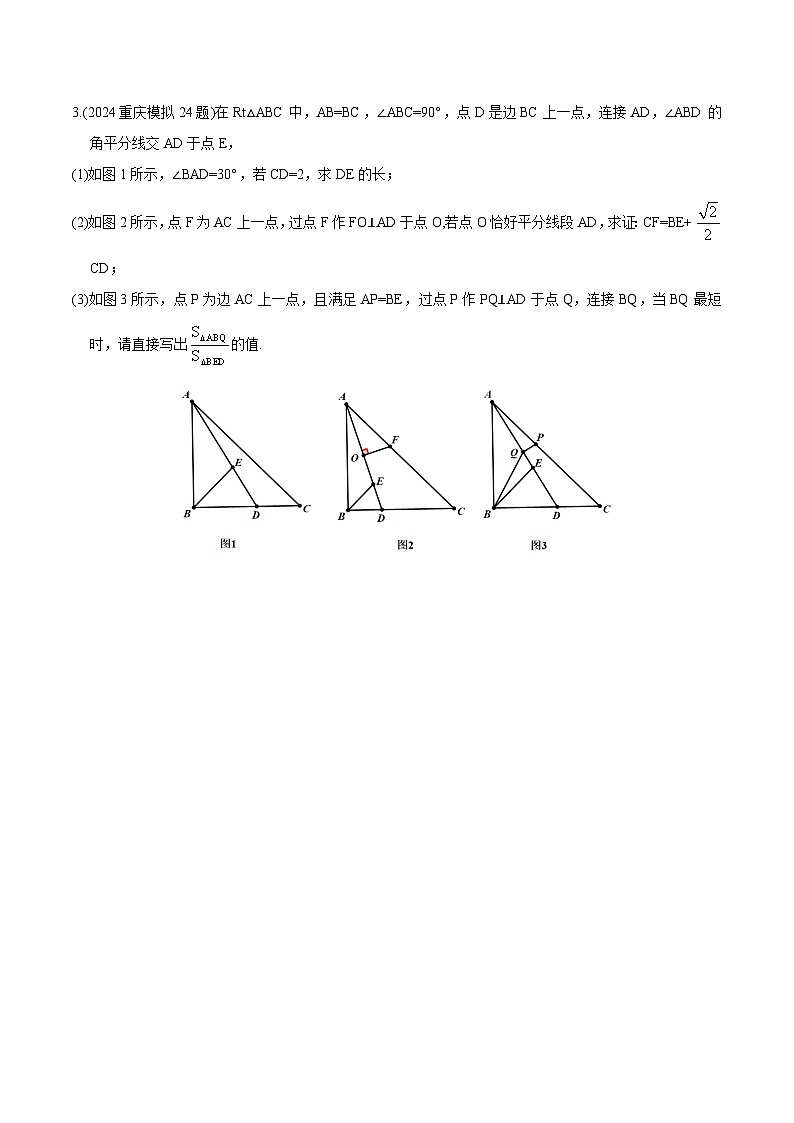
3.(2024重庆模拟24题)在Rt△ABC中，AB=BC，∠ABC=90°，点D是边BC上一点，连接AD，∠ABD的角平分线交AD于点E，
(1)如图1所示，∠BAD=30°，若CD=2，求DE的长；
(2)如图2所示，点F为AC上一点，过点F作FO⊥AD于点O,若点O恰好平分线段AD，求证：CF=BE+CD；
(3)如图3所示，点P为边AC上一点，且满足AP=BE，过点P作PQ⊥AD于点Q，连接BQ，当BQ最短时，请直接写出的值.
解：(1)如图，设BD=m,则AB=m,而BA=BC，得m+2=m,得m=+1，AD=2+2，由角平分线定理得AE：DE=AB：BD，故DE=2
另法，连接CE，易知△BEA≌△BEC，得∠DCE=30°，而∠ADB=60°，故∠DEC=30°，故DE=DC=2
过点D作DM⊥AC于点M，连接OB、OM,O为AD的中点，故OB=OM=OA=OD，设∠CAD=α，∠BAD=β，则∠BOD=2β，∠MOD=2α，故∠BOM=90°，而∠DOF=90°，故∠BOE=∠MOF；而∠BEO=180°-β-45°=135°-β，∠OFM=90°+α=90°+45°-β=135°-β，即有∠BEO=∠OFM，于是△BOE≌△MOF，BE=FM，而CM=CD，故CF=BE+CD
过点A作AG⊥AB交QP延长线于点G，作BFAD于点F，∠BEF=45°+∠BAD，∠APQ=90°-∠PAQ=90°-(45°-∠BAD)=45°+∠BAD,故∠BEF=∠APQ，而AP=BE,∠AQP=∠BFE,故△APQ≌△BEF，
而AQ=BF,∠BAF+∠GAQ=90°，∠ABF+∠ABF=90°得∠GAQ=∠ABF,∠BFA=∠AQG=90°,得△AGQ≌△BAF，AG=AB，设AB=2，则点Q在以AG为直径的圆上运动，圆心为M，当B、Q、M共线时BQ取最小值；此时BQ=-1，,而BD=-1，由角平分线定理知SABE：SBDE=2:(-1),,故
4.(2024安徽中考23题)如图，在Rt△ABC中，∠ABC=90°，点E是AC上一动点，连接BE，将BE绕点B逆时针旋转90°得到BD，连接DE交BC于点F
(1)如图1，若AB=4，∠C=30°，BE⊥AC，求DE的长；
(2)如图2，若CB=CE，连接CD，在EC上截取EM=CD，过点M作EC的垂线交BC于点N，交ED于点K，当CF=2AE时，求证：NF+DF=MN；
(3)如图3，△ABC中，若BE=CE，且∠BEC=45°，BE=4，点P为射线EA上一动点，连接BP，将BP点B逆时针旋转60°得到BQ，连接EQ，请直接写出线段EQ的最小值.
解：(1)如图，易知AE=2，DE=2；
(2)过点D作DG⊥EC于点G，交CF于点H，设∠CED=ɑ，△BDE为等腰直角三角形，CB=CE，得∠BCE=90°-2ɑ，于是∠CHF=∠CHG=2ɑ，而∠HDF=90°-ɑ得∠DFH=90°-ɑ，故DH=FH，可得NF=NK；易知△BAE≌△BHD，DH=AE，
又CF=2AE，故HD=HC=HF，故∠CDF=90°；∠DCF=ɑ=∠MEK，CD=EM，∠EMK=∠CDF，得△EMK≌△CDF，DF=KM
于是MN=NK+MK=NF+DF即有MN=NF=DF
(3)以BE为边长作等边△BEH，连接QH，易知△BPE≌△BQH，由瓜豆原理可知点Q在直线QH上运动，当EQ⊥QH时，EQ取最小值，此时∠EHQ=75°，EH=4，由sin75°=，故EQmin=
5.(2024重庆中考模拟24题)在△ABC中，D为直线AC上一动点，连接BD，将BD绕点B逆时针旋转90°得到BE，连接DE与AB相交于点F
如图1，若D为AC的中点，∠BAC=90°，AC=4，BD=，连接AE，求线段AE的长；
如图2，G是线段BA延长线上一点，D在线段AC上，连接DG、EC，若∠BAC<90°，EC⊥BG，∠ADE=∠DBC，∠DBC+∠G=∠EBF，证明：BC=2AD+DC
如图3，若△ABC为等边三角形，AB=6，点M为线段AC上一点，且2CM=AM,点P是直线BC上的动点，连接EP、MP，EM，请直接写出当EP+MP最小时EPM的面积.
解：(1)过点E作EG⊥AB于点G，由∠ABD+∠ABE=90°，∠ABD+∠ADB=90°，得∠ABE=∠ADB，而BD=BE，∠EGB=∠BAD=90°得△ABD≌△GEB，故BG=AD=2，而EG=AB=5，得AG=3，故AE=
(2)第一步：过点B作BH⊥BC且BH=BC，连接HE、HA，由∠CBH=∠DBE=90°，得∠HBE=∠CBD，而BD=BE，得△BEH≌△BDC；同时∠ADE=∠DBC，而∠ADE+∠BDE=∠DBC+∠BCD，故∠BCD=45°，于是H在CA的延长线上；
第二步：∠DBC+∠G=∠EBF，而∠DBC=∠HBE，∠EBF=∠HBE+∠EBA，于是得∠ABH=∠G；
第三步：BG⊥EC，∠ABD+∠ABE=90°，而∠ABE+∠BEC=90°，故∠BEC=∠GBD；而∠ABH+∠ABC=90°，∠BCE+∠ABC=90°，故∠BCE=∠ABH，于是∠BCE=∠G，又BE=BD，故△BCE≌△DGB，故DG=BC；
而BC=BH,得BH=DG，得△ADG≌△AHB，于是AD=AH，即有DH=2AD，于是BC=2AD+DC
(3)以BC为边作正△BCH，同时取点M关于BC的对称点M′，连接PM′，PM=PM′，PE+PM=PE+PM′；
作BQ⊥BA且BQ=BA，易知△BQE≌△BAD，∠Q=∠BAD=60°，由瓜豆原理知点E在直线QE上运动，当M′E⊥QE时，PE+PM取最小值，此时EH=，PM=，S=
6.(2024余姚中考二模)
【基础巩固】如图1，P是△ABC内部一点，在射线BP上取点D、E，使得∠CEP=∠ADP=∠ABC，求证：△ABD~△BCE
【尝试应用】如图2，在Rt△ABC中，∠BAC=90°，AB=AC，D是AC上一点，连接BD，在BD上取点E、F，连接CE、AF，使得∠AFD=∠CED=45°，若BF=2，求CE的长；
【拓展提高】如图3，在Rt△ABC中，∠BAC=90°，∠ACB=30°，D是AC上一点，连接BD，在BD上取点E，连接CE，若∠CED=60°，求△BCE的正切值；
解：(1)由∠ADE=∠ABC得∠1+∠2=∠1+∠3，得∠2=∠3；由∠ADE=∠CEP得∠ADB=∠BEC，故△ABD~△BCE；
同理易知△ABF~△BCE，故，BF=2，故CE=2；
在BD上取一点F使∠AFD=60，由(1)(2)知△ABF~△BCE，，设BE=8t，则DE=5t，AF=4t，得AG=2t，由射影定理知AG2=BG·DG，设DG=x，则有x(13t-x)=(2t)2,得x=t，故FG=4t，BG=12t；而∠BCE=∠ABF，故tan∠BCE=tan∠ABF=
7.在△ABC中，AB⊥BC,∠C=45°,点E是BC边上的一点(不含端点)，F是AC上一点，将线段AB绕点B顺时旋转ɑ得到线段BD，连接CD
如图1，已知ɑ=135°，连接DE、EF,若D、E、F三点共线，DF⊥BC，垂足为E,且CF=2，,求CD的长；
如图2，将△ABC沿着AC翻折得△MAC，若E、N分别为BC、MC的中点，连接AN、ME交AN、AC于点P、F，连接CP，若∠BCD=∠BAP，求证：CP+2PM=2CD
如图3，已知ɑ=150°，AB=2，连接DC、DE,G为射线DE上一点，连接GC、GB，将线段BC沿着CG翻折得到CB′，若点B′落在DE的延长线上，当DG取最大值时，连接GA，P是△ABG内部一动点，请直接写出(PG+PB+PA)2的最小值
解：(1)设BE=m，则AB=m+2，得m=5或-7(舍)，DE=5，故CD=
作BG⊥CD，CH⊥EM于点H，由BD=BC知CD=2CG，∠BCD=∠BAP，∠BAP=∠MNP=∠MCH，即∠MCH=∠BCG，故△MCH≌△BCG，CH=CG，同时△APM≌△MHC，MP=CH，MP=CH；而tan∠MCH=2,MH=2CH，故PH=CH，即有PC=CH，故CD-PM=CD-CG=CH=PC，故CP+2PM=2CD
如图，由CB=CD=CB,知∠1=∠2=∠3，故点C、D、B、G四点共圆，圆心为O，当D、O、G共线时，DG可取最大值；此时E为BC的中点，∠4=30°；
如图，将△ABP绕点A顺时针旋转90°，同时缩小为原来的一半，即△AIJ，此时PI=PA，IJ=PB,PG+PB+PA=PG+PI+IJ，当点G、P、I、J共线时可取最小值，AJ=1，AN=1，EG=，GN=2-，故GJ2=
8.如图，△ABC是等边三角形，△BDE是顶角为120°的等腰三角形，BD=DE,连接CD、AE
(1)如图1，连接AD，若∠ABE=60°，AB=BE=，求CD的长；
(2)如图2，若点F是AE的中点，连接CF、DF，求证：CD=2DF；
(3)如图3，在(2)的条件下，若AB=2，BD=2，将△BDE绕点B旋转，点H是△AFC内部的一点，当DF最大时，请直接写出的(2HA+HF+HC)2最小值.
解：(1)作CG⊥BD于点G，易知CG=，BG=，故CD=
方法一：延长DF至点M，使FM=FD，连接AM、CM，易知△FDE≌△FMA，故AM=DE，∠MAF=∠DEF；而DE=BD得AM=BD；而∠CBD+∠ABE=270°，∠BAE+∠BEA+∠ABE=180°，得∠CAM=∠CAB+∠BAE+∠FAM=60°+∠BAE+∠BEA+30°=90°+∠BAE+∠BEA=90°+180°-∠ABE=270°-∠ABE，即有∠CAM+∠ABE=270°，故∠CAM=CBD，又CA=CB，故△CAM△CBD，得CM=CD，∠ACM=∠BCD，而∠ACM+∠MCB=60°得∠BCD+∠MCB=60°得∠MCD=60°，故△MCD为等边三角形，故DM=CD，即有CD=2DF
方法二：延长ED至点N，使DN=DE，连接BN、AN，易知BDN为等边三角形，同时BD=BN，BC=BA，∠ABN=∠CBD，故△ABN≌△CBD，得CD=AN，而F、D分别为AE、NE的中点，故AN=2DF，即有CD=2DF
(3)易知当点C、B、D共线时，CD取最大值，此时DF取最大值；如图所示，此时CD=2+2，DF=+1，CF=3+，将△FCH逆时针旋转90°同时按比例缩小为1/2得△CTS，此时HS=CH，ST=HF，2HA+HF+HC=2(AH+CH+HF)=2(AH+HS+ST),当A、H、S、T共线时取最小值，此时(2HA+HF+HC)2=32+=18+
9.在正方形ABCD中，点G是边AB上的一个动点，点F、E在边BC上，BF=FE=AG，且AGAB，GF、DE的延长线相交于点P
(1)如图1，当点E与点C重合时，∠P的度数=___45°______
(2)如图2，当点E与C不重合时，在点G的运动过程中，∠P的度数是否发生变化，若不变，求出∠P的度数，若变化，请说明理由；
(3)在(2)的条件下，如图3，过D作DN⊥GP于点N，连接CN、BP，取BP的中点M，连接MN，在点G的运动过程中，求的值(直接写出结果即可)
解：(2)连接AC、BD交于点O，连接OG、OF,易知OA=OB，∠OAG=∠OBF=45°，AG=BF，得△OAG≌△OBF，OG=OF，∠AOG=∠BOF，而∠AOG+∠BOG=90°故∠BOF+∠BOG=90°，即∠FOG=90°，故∠OFG=45°；而O为BD的中点，F为BE的中点，故OF||OP，故∠P=45°
(3)方法一：连接AC、BD交于点O，连接OM、CM，易知OM||PD，∠1=∠2；∠COM=90°-∠1；而∠CDN=∠NDP+∠CDE=∠NDP+45°-∠2=90°-∠2，故∠COM=∠CDN；同时CD=OC，而PD=DN，PD=2OM，故ON=OM，即有，故△MSN~△CDN，故
方法二：取PD的中点S，连接SM，易知SM||BD，故∠DQS=∠QSM,而∠DQS=90°-∠2，∠CDN=∠NDS+45°-2=90°-∠2，即有∠NSM=∠CDN；同时BD=2SM,又BD=CD，有，又ND=NS，故，△NDC~△NSM，故
10.已知，在△ABC中，AB=BC，∠ABC=120°，以AB为边向下作一个△ABD且∠ADB=60°，连接CD
(1)如图1，若DA⊥AB，当AB=3时，求线段CD的长度；
(2)如图2，若点E是线段CD的中点，连接BE，猜想线段BD、AD、BE之间的数量关系，并给出证明；
(3)在(2)的条件下，当AE+CE取最小值时，请直接写出sin∠CAE的值；
解：(1)
BD=AD+2BE或BD=AD-2BE
方法一：延长CB至点F使BF=BC，连接AF，易知DF=2BE，△ABF为等边三角形，同时∠AFB=∠ADB=60°，故A、B、F、D共圆，由托勒密定理知AF·BD=AB·AD+BF·DF，即有BD=AD+2BE
方法二：延长CB至点F使BF=BC，连接AF，易知DF=2BE，ABF为等边三角形，同时作等边△DFG，易知△FDB≌△FGA，BD=AG=AD+DG=AD+2BE，即BD=AD+2BE
而第二种情形如下图，同理可得BD=AD-2BE；
综上所述：BD=AD+2BE或BD=AD-2BE；
易知点D在以O1为圆心，O1A为半径的圆上(注意此时∠AO1B=120°，O1A=O1B)，设AB=2，连接CO1，取其中点O2，连接O2E，易知O2E=1，点E在以O2为圆心，1为半径的圆上运动(瓜豆原理)；
解三角形△CBO1，可得CO1=2，CO2=，在CO2上取一点G，使O2G=，此时有，故△O2EG~△O2CE，得EG=CE，故AE+CE=(AE+CE)=(AE+EG),当A、E、G共线时，取最小值，
此时，作O1M、GN分别垂直于AC，解三角形可知CN=，AN=，GN=，sin∠CAE=(此处省略很多字)
11.在Rt△ABC中，∠BAC=90°
如图1，D、E分别在BC、BA的延长线上，∠ADE=2∠CAD，求证：DA=DE；
如图2，在(1)的条件下，点F在BD上，∠AFB=∠EFD，求证：∠FAD=∠FED；
如图3，若AB=AC，过点C作CN||AB，连接AN，在AN上取点G，使AG=AC，连接BG交AC于H，连CG，试探究CN、CH、GN之间满足的数量关系式，并给出证明.
解：(1)过点D作DM⊥AE于点M，易知DM||CA，设∠CAD=α，则∠ADE=2α，而∠ADM=∠CAD，故DM平分∠ADE，故DA=DE;
延长EF至点P，使FP=FA，连接PB、PD，设∠AFB=β，则∠BFP=β，故△ABF≌△PBF，△ABD≌△PBD，于是DP=DA，而DA=DE得DP=DE，故∠FED=∠DPF，而∠DPF=∠FAD，得∠FAD=∠FED
设∠ABG=γ，则∠AGB=γ，∠CAG=90°-2γ，得∠AGC=∠ACG=45°+γ，于是∠CGH=45°，过点C作CT⊥GH交AG于点T，可得∠GCT=45°，同时∠HCG=∠TGC，CG=GC，得△CGH≌△GCT，CT=GH，GT=CH；同时∠NTC=∠NCT=90°-γ，故NT=NC，于是GH=NT=GN+GT，即有GH=GN+CH
12.如图，四边形ABCD中，AB=CD，∠ABC+∠BCD=270°，
(1)求∠A+∠D的度数；
(2)连接AC，若∠ACB=45°，求证：BC2+2AC2=AD2；
(3)点E、F分别为线段BC和AD上的点，点G是线段EF上任意一点且△GAB和△GCD的面积相等，过点D作DH⊥EF，DH交直线EF于点H，连接AH，若AD=4，求AH的最小值；
解：(1)∠A+∠D=90°
方法一：作DG⊥AC于点G并延长DG至点F使GF=GC,易知∠F=45°，由(1)知∠BAD+∠ADC=90°，而∠CAD+∠ADC+∠CDG=90°得∠CDG=∠BAC，又AB=CD，故△ABC≌△DCF，得DF=AC，CF=BC，在ADG中，有AD2=AG2+DG2，而AG=AC+CG=AC+BC，DG=DF-GF=AC-BC，即有故BC2+2AC2=AD2
方法二：将ACD绕点C顺时针旋转90°得△CEF，连接AE、AF，易知CF=CD,而AB=CD得AB=CF；CA=CE，AE=AC，由∠ABC+∠BCD=270°，∠FCD=90°得∠ABC+∠BCF=180°，故AB||CF,故ABCF为平行四边形，AF=BC，∠FAC=∠ACB=45°，即有∠EAF=90°，有AE2+AF2=EF2，故BC2+2AC2=AD2
延长AB、DC于点Q，过点G作GM⊥AB，GN⊥CD，由已知得GM=GN，故点G在∠AQD的平分线上，而点G是EF上任意一点，故EF即在∠AQD的平分线上，而∠AQD=90°知点Q在以AD为直径的圆上运动，延长QF交圆于点P，易知P为半圆的中点，连接PD，PD=2，而∠PHD=90°，点H在以PD为直径的圆上运动，圆心为PD的中点W，当A、H、W，当A、H、W共线时，AH取最小值，最小值为
13.在Rt△ABC中，∠C=90°，将△ABC绕点A顺时针旋转得到△ADE，旋转角小于∠CAB，点B的对应点为点D，点C的对应点为点E，DE交AB于点O，延长DE交BC于点P，
如图1，求证：PC=PE；
当AD||BC时，
①如图2，若CA=6，CB=8，求线段BP的长；
②如图3，连接BD、CE，延长CE交BD于点F，判断F是否为线段BD的中点，并说明理由.
解：(1)连接PA，AE=AC，PA=PA，故△PAE≌△PAC，得PE=PC
(2)由(1)知∠APE=∠APC，而AD||BC，∠APC=∠PAD，故∠PAD=∠APE，故AD=PD，而DE=8，得PE=2，故PC=2，BP=6；
(3)延长EF交AD延长线于点G，易知△ACG~△CPA，得AG=18，故DG=8，而BC=8，故F为BD的中点
14.[操作与思考]如图1，在△AOB中，∠AOB＝30°，AO＝3，BO＝4，以AB为边按逆时针方向作等边三角形ABC，连接OC，请你以AO为边按顺时针方向作等边三角形AOD，再连接BD，直接写出OC的长 ；
[迁移与应用]如图2，在△AOB中，∠AOB＝60°，AO＝3，BO＝4，以AB为斜边按逆时针方向作直角三角形ACB，其中∠ACB＝90°，∠BAC＝30°，若D为OB中点，连接CD，求CD的长；
[拓展与创新]如图3，△ABC和△ADE均为等边三角形，AB＝8，AD＝3，M为BC中点，连接DM、EM和BD，当∠DME＝30°时，直接写出BD的长 ．
解：(1)以OA为边在左侧作等边△AOF，连接BF，AO=AF，AB=AC，∠OAC=∠BAF，得△ABF≌△ACO，OC=BF,同时∠AOF=60°，∠ABO=30°，故∠BOF=90°，得BF=5，故OC=5；
方法一：延长BC至点G使CG=CB，连接AG，易知△ABG为等边三角形，C为BG的中点，连接OG，易知OG=2CD；以AO为边在左侧作等边△AOF连接BF，由(1)知BF=OG，作FH⊥BO于点H，得OH=，FH=，于是BF=，故CD=
方法二：延长BC至G，使CG=CB，连接OG，同时作等边△OBQ，连接QG，连接AG，易得△BAQ≌△BGQ，GQ=3，连接DQ，作GI⊥OB于点I，易知AB=，BI=1，GI=2，于是可得OG=，故CD=
以DM为边作等边△DMG，连接EG、AM，由(2)得GE=AM=4，∠GME=90°，设DM=n，ME=a，则有，同时在△DEM中，有要得(思路1：此处可得，但计算结果过于复杂，直接放弃)
延长DM至点F，使MF=MD，连接CF，易知△MBD≌△MCF，连接EF，则EF=，在△MEF中，可得即有由此可得m=，即BD=
方法二：取点A关于DE的对称点F，连接FD、FE、FA交DE于点H，连接MA、MH，作MGAF于点G，易知△DEF为等边三角形，∠DFE=60°，而∠EME=30°，故D、E、M在以点F为圆心，3为半径的圆上，得FM=FD=FE=3，设FG=a，MG=b，AF=3，于是得，MH=，又，∠BAD=∠MAH，得△ABD~△AMH,有，于是DB=