2024年湖南省三湘大联考初中学业水平考试模拟试卷（三）数学

这是一份2024年湖南省三湘大联考初中学业水平考试模拟试卷（三）数学，共5页。

注意事项：
1.答题前，请考生先将自己的姓名、准考证号填写清楚，并认真核对条形码上的姓名、准考证 号、考室和座位号；
2.必须在答题卡上答题，在草稿纸、试题卷上答题无效；
3.答题时，请考生注意各大题题号后面的答题提示；
4.请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；
5.答题卡上不得使用涂改液、涂改胶和贴纸；
6.本学科试卷共26道题目，考试时量120分钟，满分120分.
一、选择题(在下列各题的四个选项中，只有一项是符合题意的.请在答题卡中填涂符合题意 的选项，本大题共10个小题，每小题3分，共30分)
1.2023 的相反数是 ( ) A B.2023 C.-2023
2.现代足球起源于中国古代山东临淄(今淄博市)的球类游戏“蹴鞠”,后经阿 拉伯人由中国传至欧洲，逐渐演变发展为现代足球.现代足球由32块外表 皮缝制而成，其中，12块黑的正五边形，20块白的正六边形.在正五边形和
正六边形中，既是轴对称图形，又是中心对称图形的是 ( )
A. 正五边形 B.正六边形
C. 正五边形和正六边形 D. 都不是
3.将多项式x²-2x+1 因式分解的结果为 ( )
A.(x+1)² B.(x+1)(x-1) C.(x-1)² D.x(x+2)+1
4.如图，已知点D 是△ABC 的 BC 边延长线上一点，且满足∠A=85°,∠B=25°, 则∠ACD
的度数为 ( )
A.100° B.110° C.40° D.70°
第4题图
第6题图
5.受国内宏观政策利好的影响，2023年元旦和春节的旅游市场迎来“开门红”,为整个一季 度的发展奠定了基础、增添了信心， 一季度，国内旅游总人次12.16亿，同比增长46.5%.
其中数据12.16亿用科学记数法表示为 ( )
×10⁸ ×10¹? ×10⁹ D.1216×10⁶
6.如图，AB 是OO 的直径，CD 为弦，CD⊥AB 于点E, 连接AC,AD, 则下列结论正确的是 ( )
A.AC=BC B.BC=BD C.OE=BE D. ∠CAD=∠CDA
7.袁隆平院士被誉为“世界杂交水稻之父”,为研究出高产水稻付出了毕生心血，他培育的超
级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势，从稻田中随
机抽取10株水稻苗，测得苗高(单位：cm);27,23,23, 25,23,24, 22,24,25,26,则这组数据
的平均数和中位数分别是 ( )
A.24.2,23 B.21.9,24 C.24.2,24 D.24,25
三湘大联考 初中学业水平考试数学模拟试卷(三) 第1页(共4页)
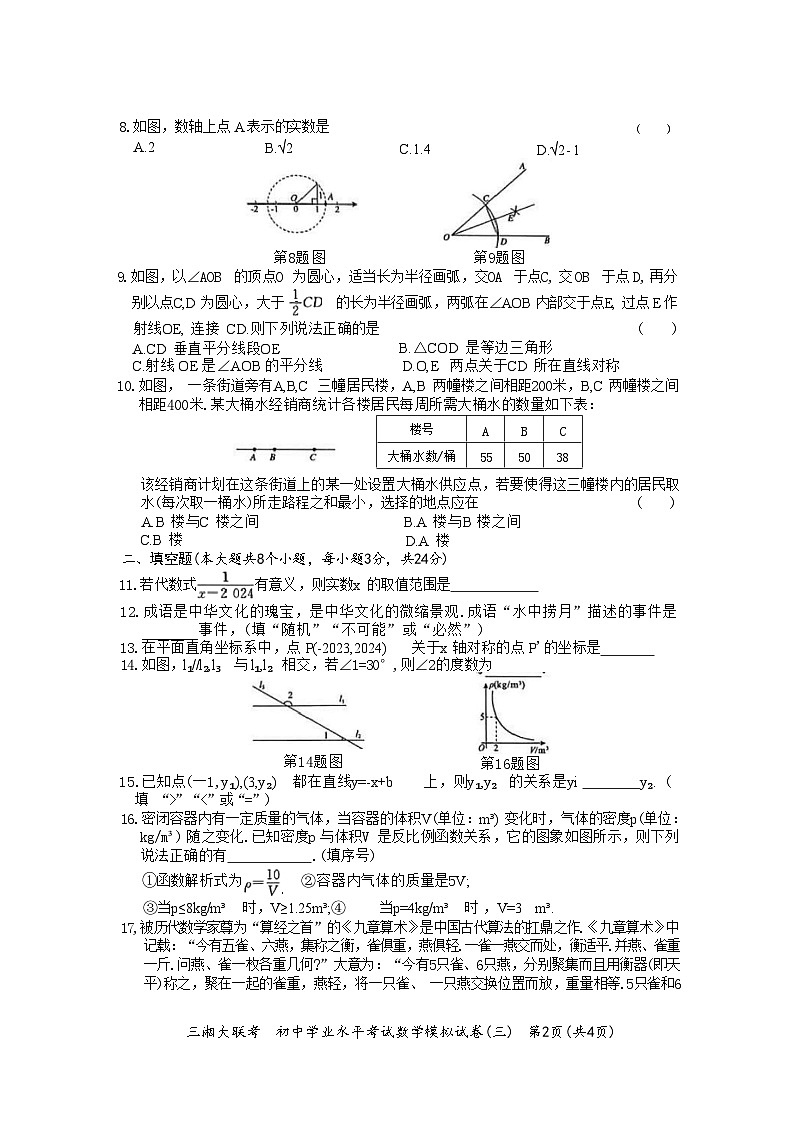
8.如图，数轴上点 A 表示的实数是 ( )
A.2 B.√2 C.1.4 D.√2- 1
第8题图 第9题图
9.如图，以∠AOB 的顶点O 为圆心，适当长为半径画弧，交OA 于点C, 交 OB 于点 D, 再分
别以点C,D 为圆心，大于 · 的长为半径画弧，两弧在∠AOB 内部交于点E, 过点 E 作
射线OE, 连接 CD.则下列说法正确的是 ( )
A.CD 垂直平分线段OE B. △COD 是等边三角形
C.射线 OE 是∠AOB 的平分线 D.O,E 两点关于CD 所在直线对称
10.如图， 一条街道旁有A,B,C 三幢居民楼，A,B 两幢楼之间相距200米，B,C 两幢楼之间 相距400米.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表：
该经销商计划在这条街道上的某一处设置大桶水供应点，若要使得这三幢楼内的居民取
水(每次取一桶水)所走路程之和最小，选择的地点应在 ( )
A.B 楼与C 楼之间 B.A 楼与B 楼之间
C.B 楼 D.A 楼
二、填空题(本大题共8个小题，每小题3分，共24分)
11.若代数式有意义，则实数x 的取值范围是
12.成语是中华文化的瑰宝，是中华文化的微缩景观.成语“水中捞月”描述的事件是 事件，(填“随机”“不可能”或“必然”)
13.在平面直角坐标系中，点 P(-2023,2024) 关于x 轴对称的点 P'的坐标是 14.如图，l₁//l₂,l₃ 与 l₁,l₂ 相交，若∠1=30°,则∠2的度数为
第14题图 第16题图
15.已知点(一1,y₁),(3,y₂) 都在直线y=-x+b 上，则y₁,y₂ 的关系是yi y₂. (填 “>”“<”或“=”)
16.密闭容器内有一定质量的气体，当容器的体积V(单位：m³) 变化时，气体的密度p(单位： kg/m³) 随之变化.已知密度p 与体积V 是反比例函数关系，它的图象如图所示，则下列 说法正确的有 .(填序号)
①函数解析式为
②容器内气体的质量是5V;
;
③当p≤8kg/m³ 时，V≥1.25m³;④ 当p=4kg/m³ 时 ，V=3 m³ .
17,被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中 记载：“今有五雀、六燕，集称之衡，雀俱重，燕俱轻.一雀一燕交而处，衡适平.并燕、雀重 一斤.问燕、雀一枚各重几何?”大意为：“今有5只雀、6只燕，分别聚集而且用衡器(即天 平)称之，聚在一起的雀重，燕轻，将一只雀、 一只燕交换位置而放，重量相等.5只雀和6
三湘大联考 初中学业水平考试数学模拟试卷(三) 第2页(共4页)
楼号
A
B
C
大桶水数/桶
55
50
38
只燕的总重量为1斤.问雀、燕每1只各重多少斤?”若假设一只雀重 x 斤， 一只燕重 y 斤，则 x= ,y=
18. 如图，Rt△ACB 中， ∠C=90°, 已 知AB=13 cm,AC=5 cm,动点 P 从
点B 出发沿射线 BC 以 1 cm/s 的速度运动，动点Q 从 点A 出发沿射
线AB 以2 cm/s 的速度运动，设运动时间为ts, 当以B,P,Q 为顶点
的三角形和△ABC 相似时，t 的值为
三、解答题(本大题共8个小题，第19、20题每小题6分，第21、22题每小题8分，第23、24 题每小题9分，第25、26题每小题10分，共66分，解答应写出必要的文字说明、证明过程或 演算步骤)
19.(6分)计算：
20.(6分)解方程：x²-6x+2=0.
21.(8分)每年12月2日是“全国交通安全日”,每一位公民任何时
候都应该遵守交通规则.某学校门前有一直行马路，为方便学生
过马路，交警在门口设有一定宽度的斑马线，斑马线的宽度 DE
为6米.现有一旅游车在路口遇红灯刹车停下，如图，汽车里司
机A 与斑马线前后两端的视角∠FAE,∠FAD 的大小分别为
15°和30°,司机与车头的水平距离BC 为1米，与车顶的垂直距离为0.2米. (1)旅游车高约多少米?
(2)为安全起见，规定车头距斑马线后端的水平距离CD 不得小于3米，试问该旅游车停 车是否符合上述安全标准? (E,D,C,B 四点在平行于斑马线的同一直线上)
(参考数据：tan 15⁰≈0.27,sin15°≈0.26,cs 15°≈0.97√3≈1.73,√2≈1.41)
22.(8分)教育部办公厅关于推广部分地方义务教育课后服务有关创新举措和典型经验的 通知指出：“……开展丰富多彩的文体活动、阅读、兴趣小组以及社团活动，提高课后服务 质量水平.”某校积极响应政策，为了进一步促进校园文化建设和学生全面发展，开设了 适合学生素质发展的课后服务内容，该内容分为4个类别，分别为音乐类(A), 美术类(B), 科技类(C), 体育类(D), 为了解学生对以上内容的喜欢程度，现抽取了部分学生参与调 查，并根据调查结果绘制了如图所示的两幅不完整的统计图：
请根据以上提供的信息，解答下列问题：
(1)本次调查所抽取的学生人数为 ;
(2)请补全上面的条形统计图和扇形统计图；
(3)扇形统计图中，C 对应的扇形圆心角的度数为 j
(4)若该校共有学生3000人，请估计其中喜欢“科技类”的学生人数.
23.(9分)2023年9月15日至17日，第二届湖南旅游发展大会在郴州市隆重举行，大会吉 祥物“山侠”和“水仙”,以郴州的“山之侠气”“水之仙气”为灵感创作.
(1)某商店用3600元共购进“山侠”和“水仙”两种吉祥物公仔110个，用于购买“山侠”公 仔与购买“水仙”公仔的总费用相同，且“山侠”公仔的单价是“水仙”公仔的1.2倍.求该 商店购进的“山侠”和“水仙”公仔的单价分别是多少元?
(2)吉祥物很受欢迎，公仔很快就卖完了，该商店计划用不超过10200元的资金再次购 进“山侠”和“水仙”两种吉祥物公仔共300个.已知两种公仔的进价不变，求“山侠”公仔 最多能购进多少个.
24.(9分)如图，以△ABC 的三边为边分别作为等边△ACD、 等边△BCF
和等边△ABE, 连接 DE 和EF.
(1)求证：DE=CF;
(2)判断四边形 CDEF 的形状，并说明理由；
(3)若AC=BC=6,AB=6√3, 求四边形CDEF 的面积.
25.(10分)如图，AD 是O圆O 的切线，A 为切点，点 B,C 是圆上 与点A 不重合的两点.
(1)如图1,若AB 是OO 的直径，AO=AC=5, 求∠DAC的 度数；
(2)如图2,当点 B 在OO 上运动时(不与点 A,C 重合), ∠DAC 与∠B 有怎样的数量关系?请说明理由.
图 1
图 2
26.(10分)我们知道：关于x 的二次函数y=ax²+bx+c(a≠0), 当系数a,b,c 确定时，该二
次函数的图象也随之确定，顶点坐标 也唯一确定.
(1)①请写出关于x 的二次函数y=3x²+2x-4 的顶点坐标： _;
②请写出关于x 的二次函数y=-x²+2x+c 的顶点坐标： ;(用含有c 的
式子表示)
(2)已知关于x 的二次函数y=z²+bx+4b, 请问该抛物线的顶点是否有最高位置或者
最低位置?如果有，求出此时b的取值；
(3)关于x 的二次函数y=x²+ mx + mn 与,这两个抛物线的顶点分别 是P₁(x₁,y₁) 和P₂(x₂,y₂), 当 - 2≤m≤2 时，是否存在实数n, 使得y₁三湘大联考 初中学业水平考试数学模拟试卷(三) 第4页(共4页)
·
: · ;