

重庆市重庆实验外国语学校2021-2022学年八年级下学期期中测试数学试卷(含答案)
展开
这是一份重庆市重庆实验外国语学校2021-2022学年八年级下学期期中测试数学试卷(含答案),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1. 下列图形中,是轴对称图形的是( )
A B. C. D.
2. 若函数有意义,则x的取值范围是( )
A. B. C. D. 一切实数
3. 下列计算正确的是( )
A. B.
C. D.
4. 如图,与位似,点O为位似中心.已知,则与的相似比为( )
A. B. C. D.
5. 下列说法正确的是( )
A. 一组对边相等,另一组对边平行的四边形是平行四边形
B. 有一个角是直角的平行四边形是矩形
C. 对角线互相垂直且平分的四边形是正方形
D. 对角线互相垂直的四边形是菱形
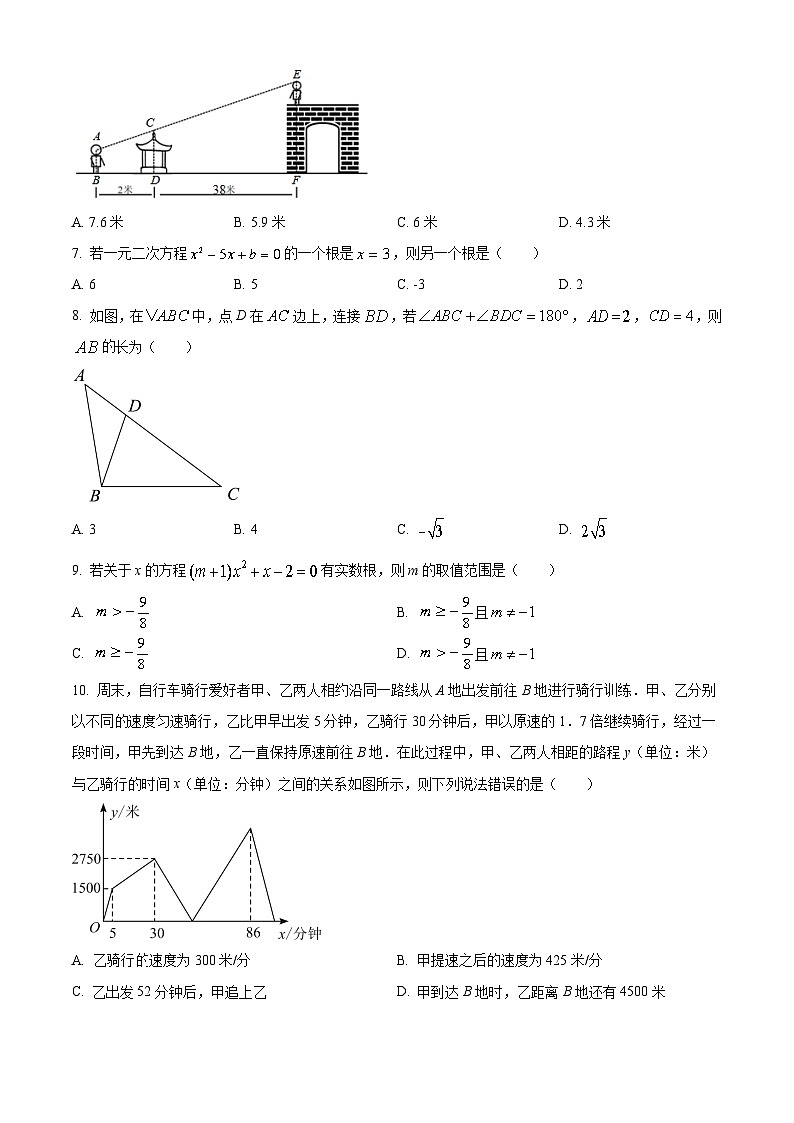
6. 某天小明和小亮去某影视基地游玩,当小明给站在城楼上小亮照相时,发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面的距离为1.6米,凉亭顶端离地面的距离为1.9米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.那么城楼的高度为( )
A. 7.6米B. 5.9米C. 6米D. 4.3米
7. 若一元二次方程的一个根是,则另一个根是( )
A. 6B. 5C. -3D. 2
8. 如图,在中,点D在边上,连接,若,,,则长为( )
A. 3B. 4C. D.
9. 若关于x的方程有实数根,则m的取值范围是( )
A. B. 且
C. D. 且
10. 周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练.甲、乙分别以不同速度匀速骑行,乙比甲早出发5分钟,乙骑行30分钟后,甲以原速的1.7倍继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则下列说法错误的是( )
A. 乙骑行速度为300米/分B. 甲提速之后的速度为425米/分
C. 乙出发52分钟后,甲追上乙D. 甲到达B地时,乙距离B地还有4500米
11. 若关于x的不等式组的解集是,关于y的分式方程的解为非负数,则所有符合条件的整数a的和为( )
A. -18B. -15C. 0D. 2
12. 如图,在边长为6的正方形中,E、F分别是边、上的点,且,连接、交于点G,在延长线上取一点P,使,连接,则下列结论正确的有( )
①,②,③,④
A. 1个B. 2C. 3个D. 4个
二、填空题:(本大题6个小题,每小题4分,共24分)将每小题的答案直接填在答题卡中对应的横线上.
13. 计算:______.
14. 若,则______.
15. 如图,点E是平行四边形的边上的一点,且,连接并延长交的延长线于点F,则______.
16. 如图,在平面直角坐标系中,点O为原点,点C在x轴正半轴上,以为边在x轴上方作矩形,若点B坐标为,平面内有一条直线恰好将矩形分成面积相等的两部分,则k的值为______.
17. 如图,在中,点D是上一点,连接,将沿翻折得到,交于点G,连接,交于点F.若点G为的中点,的面积为5,,,则点F到的距离为______.
18. 重庆某食品厂开发了一批新口味糕点,有海苔风味小贝、柠檬酸奶风味小贝、蟹黄风味小贝三种.3月初,某商店从厂家购进海苔风味、柠檬酸奶风味、蟹黄风味小贝的数量比为,由于新型口味的小贝非常受大家的喜欢,销售情况非常好.店里又紧急加购了三种小贝.其中蟹黄风味小贝增加的数量占总增加数量的,蟹黄风味小贝总数量将达到三种小贝总量的.此时海苔风味小贝与柠檬酸奶风味小贝的总数量之比为.该商店整理货物时发现两次一共购进1000个小贝,两次购进小贝的总价为4850元,第二次比第一次多花费2500元(三种小贝的进价不变且为整数).若商店在4月份需再次购进海苔风味、柠檬酸奶风味、蟹黄风味小贝的数量分别为100,150,120.则商家4月份需再次支付________元.
三、解答题:(本大题共8个小题,26小题8分,其余每小题10分,共78分)
19. 解一元二次方程:
(1)
20. 如图,在中,,是边的中线,过A作,且,连接.
求证:四边形是菱形;
若,,求四边形的面积.
先化简,再求值:,其中a为整数且满足.
22. 为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识竞赛活动.现从该校八、九年级中各随机抽取20名学生的竞赛成绩(满分10分,6分及6分以上为合格,8分及8分以上为优秀)进行整理、描述和分析,下面给出了部分信息:
九年级20名学生的竞赛成绩为:3,5,7,6,9,8,6,7,10,9,8,8,6,6,8,8,8,9,9,8.
九年级抽取的学生的竞赛成绩统计表
八年级20名学生的竞赛成绩条形统计图
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)该校八、九年级共1600名学生参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
根据以上数据分析,从一个方面评价哪个年级此次竞赛活动成绩更优异.
23. 2022年某地桑葚节于4月5日到4月20举行,热情的当地居民为游客准备了桑葚茶、桑葚酒、桑葚酱、桑葚膏等等,在当地举行的“桑葚会”上,游客不仅可以品尝纯正的桑葚茶、桑葚酒、桑葚酱、桑葚音,而且还能体验制作它们的过程.各类桑葚产品均对外销售,游客们可以买一些送给亲朋好友.已知桑葚酒是桑葚酱单价的,预计桑葚节期间全镇销售桑葚酒和桑葚酱共7500千克,桑葚酒销售额为200000元,桑葚酱销售额为125000元.
(1)求本次桑葚节预计销售桑葚酒和桑葚酱的单价;
今年因受“新冠”疫情的影响,前来参加桑葚节的游客量比预计有所减少,当地镇府为了刺激经济,减少库存,将桑葚酒和桑葚酱降价促销.桑葚酱在预计单价的基础上降低销售,桑葚酒比预计单价降低元销售,这样桑葚酱的销量跟预计一样,桑葚酒的销量比预计减少了a%,桑葚酒和桑葚酱的销售总额比预计减少了3500a元.求a的值
24. 如图,在平面直角坐标系中,直线与直线交于点,直线与x轴交于点,与y轴交于点B,将直线向下平移5个单位长度得到直线,与y轴交于点D,与交于点E,连接.
求直线的解析式;
求的面积.
在平面直角坐标系中存在点P,使得以A、E、D、P为顶点的四边形是平行四边形,请直接写出点P的坐标.
25. 材料一:对于一个四位正整数,如果满足各数位上的数字互不相同,它的千位数字与个位数字之和等于百位数字与十位数字之和,那么称这个数为“和好数”.若和好数(,,,且a、b、c、d均为整数),规定将p的十位数字与百位数字之差的3倍记为,即.
材料二:若一个数N等于另一个整数Z的平方,则称这个数N为完全平方数.
请判断3264,5342是否是“和好数”,并说明理由;如果是,请计算的值;
若正整数s,t都是“和好数”,其中,,(,,,,且m、n、x、y都是整数),当的值是一个完全平方数时,求满足条件的所有正整数s的值.
26. 如图,在平行四边形中,,于E,于G,交于F.
如图1,若,,求的长;
如图2,平行四边形外部有一点H,连接、,满足,,求证:.
(3)如图3,在上有一点M,连接,将绕着点M顺时针旋转90°得,连接、,点P为的中点,连接.在(1)的条件下,当最小时,直接写出线段的长度
参考答案与解析
一、选择题:(本大题12个小题,每小题4分,共48分)
1-6CBDABB 7-12DDCDBC
二、填空题:(本大题6个小题,每小题4分,共24分)
13. 14. 15.
16. 17. 18. 1820
三、解答题:(本大题共8个小题,26小题8分,其余每小题10分,共78分)
19. 解:(1)
移项得:
分解因式得:,
可得x-2=0或3x+1=0,
解得:x1=2,x2=.
(2)
∵a=3,b=-4,c=-1,
∵b2-4ac=16-4×3×(-1)=28>0,
∴x=,
∴x1=,x2=
20. (1)证明:∵在△CAE中,∠CAE=90°,AD是CE边的中线,
,
,
,
,
四边形是平行四边形,
,
四边形是菱形.
(2)连接BD,交AC于点O,如图所示:
四边形是菱形,
,,,
,
,
,
.
21.解:原式=
,
解不等式①,得,a≥-1,
解不等式②,得,a
相关试卷
这是一份重庆市重庆实验外国语学校2021-2022学年八年级下学期期中测试数学试卷(北师大版含答案),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份重庆市重庆实验外国语学校2023-2024学年八年级下学期数学试题(无答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年重庆实验外国语学校八年级(下)期中数学试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








