2021-2022学年北京市101中学矿大分校高二（下）期中数学试卷

这是一份2021-2022学年北京市101中学矿大分校高二（下）期中数学试卷，共16页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．（4分）已知等差数列{an}中，a1＝2，公差d＝3，则a10＝（ ）
A．29B．32C．26D．35
2．（4分）已知等比数列{an}的公比为q，前n项和为Sn，若q＝2，S2＝6，则S3＝（ ）
A．8B．10C．12D．14
3．（4分）函数f（x）＝的导函数f′（x）＝（ ）
A．B．
C．D．
4．（4分）函数y＝x﹣lnx的单调递增区间是（ ）
A．（﹣∞，0）∪（1，∞）B．（1，∞）
C．（0，+∞）D．（0，1）
5．（4分）已知某物体运动的位移s关于t的函数为s（t）＝t2+t，则当t＝2时的瞬时速度为（ ）
A．2m/sB．3m/sC．4m/sD．5m/s
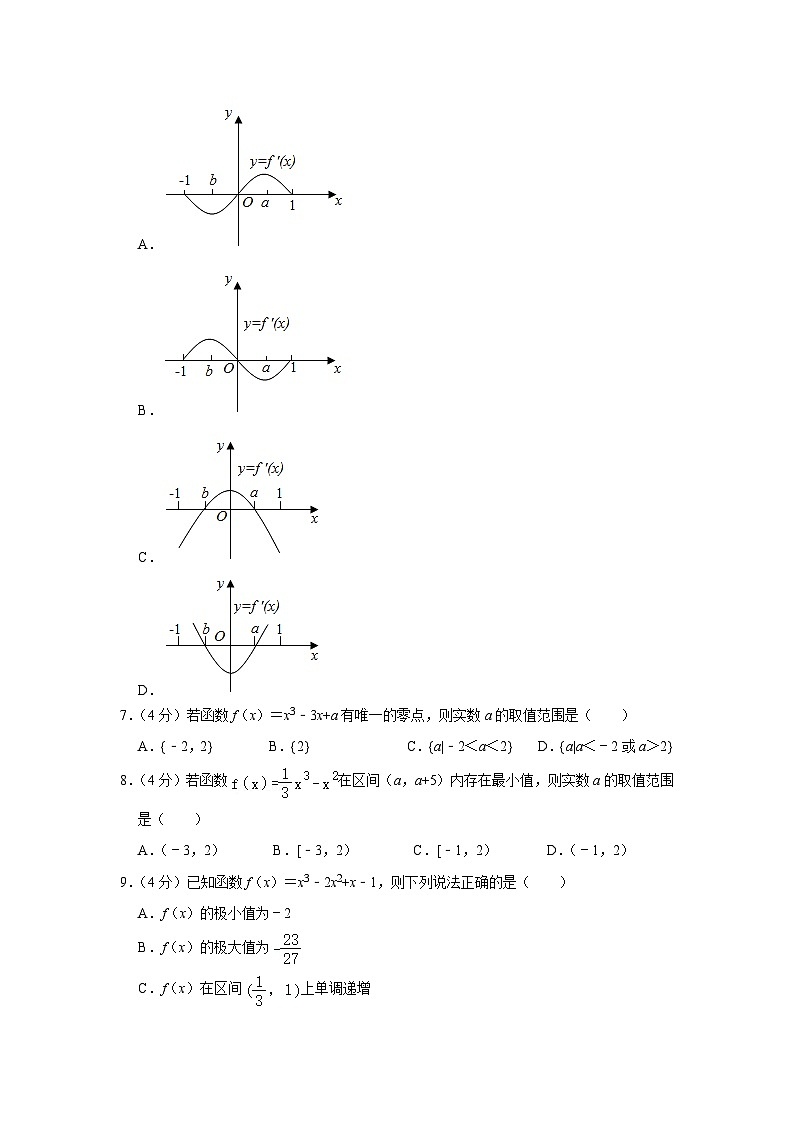
6．（4分）已知函数y＝f（x）的图象如图所示，则函数y＝f′（x）的图象可能是图中的（ ）
A．
B．
C．
D．
7．（4分）若函数f（x）＝x3﹣3x+a有唯一的零点，则实数a的取值范围是（ ）
A．{﹣2，2}B．{2}C．{a|﹣2＜a＜2}D．{a|a＜﹣2或a＞2}
8．（4分）若函数在区间（a，a+5）内存在最小值，则实数a的取值范围是（ ）
A．（﹣3，2）B．[﹣3，2）C．[﹣1，2）D．（﹣1，2）
9．（4分）已知函数f（x）＝x3﹣2x2+x﹣1，则下列说法正确的是（ ）
A．f（x）的极小值为﹣2
B．f（x）的极大值为
C．f（x）在区间上单调递增
D．f（x）在区间（﹣∞，0）上单调递减
10．（4分）等比数列{an}满足a1＝32，q＝﹣，记Tn＝a1a2…an（n∈N+），则数列{Tn}（ ）
A．有最大值，有最小值B．有最大值，无最小值
C．无最大值，有最小值D．无最大值，无最小值
11．（4分）已知﹣1，a1，a2，﹣7成等差数列，﹣3，b1，b2，b3，﹣12成等比数列，则b2•（a2﹣2a1）等于（ ）
A．﹣6B．6C．﹣12D．﹣6或6
12．（4分）函数f（x）＝（x2﹣2x）ex的图象大致是（ ）
A．B．
C．D．
二、填空题。（共4小题，共16分）
13．（4分）过点A（1，1）与曲线C：y＝x3相切的直线方程是 ．
14．（4分）函数f（x）＝x+，设f（x）在区间[1，2]与[3，5]的平均变化率为a，b，则a，b的大小关系为 ．
15．（4分）已知函数f（x）＝lnx，则＝ ．
16．（4分）若数列{an}满足：a1＝1，an+1＝an+2n，（n∈N+），则数列{an}的通项公式为 ．
三、解答题。（共4小题，共36分）
17．（10分）已知等差数列{an}满足：a1＝2，a5＝18．
（1）求数列{an}的通项公式；
（2）记Sn为数列{an}的前n项和，求正整数n的范围，使得Sn＞60n+800．
18．（10分）已知函数f（x）＝2x3+3ax2+3bx+1且在x＝1及x＝2处取得极值．
（1）求a，b的值；
（2）求函数y＝f（x）在[0，3]上的最大值与最小值的差．
19．已知函数f（x）＝x2﹣alnx﹣2．
（1）当a＝3时，求f（x）在x＝1处的切线方程；
（2）求f（x）的单调区间．
20．已知函数f（x）＝lnx﹣ax（a∈R）．
（1）当a＝1时，求函数的单调区间；
（2）若f（x）≤0恒成立，求a的取值范围．
2021-2022学年北京市101中学矿大分校高二（下）期中数学试卷
参考答案与试题解析
一、填空题。（共12小题，共48分）
1．（4分）已知等差数列{an}中，a1＝2，公差d＝3，则a10＝（ ）
A．29B．32C．26D．35
【分析】根据已知条件，结合等差数列的通项公式，即可求解．
【解答】解：在等差数列{an}中，a1＝2，公差d＝3，
则a10＝a1+9d＝2+9×3＝29．
故选：A．
【点评】本题主要考查等差数列的通项公式，属于基础题．
2．（4分）已知等比数列{an}的公比为q，前n项和为Sn，若q＝2，S2＝6，则S3＝（ ）
A．8B．10C．12D．14
【分析】由等比数列的基本量运算求出a1后，求出a3，由此能求出S3．
【解答】解：由题意得S2＝a1+2a1＝6，解得a1＝2，
∴＝8，
S3＝S2+a3＝6+8＝14，
故选：D．
【点评】本题考查等比数列的性质等基础知识，考查运算求解能力，是基础题．
3．（4分）函数f（x）＝的导函数f′（x）＝（ ）
A．B．
C．D．
【分析】根据基本初等函数和商的导数的求导公式求导即可．
【解答】解：．
故选：B．
【点评】本题考查了基本初等函数和商的导数的求导公式，考查了计算能力，属于基础题．
4．（4分）函数y＝x﹣lnx的单调递增区间是（ ）
A．（﹣∞，0）∪（1，∞）B．（1，∞）
C．（0，+∞）D．（0，1）
【分析】易得函数的定义域为（0，+∞），由导数y′＝1﹣＞0结合定义域可得答案．
【解答】解：由题意可得函数的定义域为（0，+∞），
求导数可得y′＝1﹣，
令1﹣＞0结合定义域可解得x＞1
故函数的单调增区间为（1，+∞）
故选：B．
【点评】本题考查利用导数研究函数的单调性，注意的定义是解决问题的关键，属中档题．
5．（4分）已知某物体运动的位移s关于t的函数为s（t）＝t2+t，则当t＝2时的瞬时速度为（ ）
A．2m/sB．3m/sC．4m/sD．5m/s
【分析】由已知结合导数的定义即可求解．
【解答】解：因为s（t）＝t2+t，
所以s′（t）＝2t+1，
则当t＝2时的瞬时速度为5．
故选：D．
【点评】本题主要考查了导数的定义的应用，属于基础题．
6．（4分）已知函数y＝f（x）的图象如图所示，则函数y＝f′（x）的图象可能是图中的（ ）
A．
B．
C．
D．
【分析】分析x∈（﹣1，b）和x∈（b，a）时，函数f（x）的单调性，确定f'（x）与0的大小关系，即可得解．
【解答】解：由y＝f（x）的图象可知，
当x∈（﹣1，b）时，f（x）单调递减，所以f'（x）＜0，排除选项B和D；
当x∈（b，a）时，f（x）单调递增，所以f'（x）＞0，排除选项A，
故选：C．
【点评】本题考查利用导数判断函数的单调性，理解函数的单调性与导数之间的联系是解题的关键，考查逻辑推理能力，属于基础题．
7．（4分）若函数f（x）＝x3﹣3x+a有唯一的零点，则实数a的取值范围是（ ）
A．{﹣2，2}B．{2}C．{a|﹣2＜a＜2}D．{a|a＜﹣2或a＞2}
【分析】由导数求得函数的极大值和极小值，三次函数有唯一零点，则极大值小于0或极小值大于0．
【解答】解：f（x）＝x3﹣3x+a，则f′（x）＝3x2﹣3＝3（x+1）（x﹣1），
当x＜﹣1或x＞1时，f′（x）＞0，﹣1＜x＜1时，f′（x）＜0，
因此f（x）在（﹣∞，﹣1）和（1，+∞）上单调递增，在（﹣1，1）上单调递减，
所以f（x）的极大值为f（﹣1）＝2+a，f（x）的极小值为f（1）＝﹣2+a，
因为f（x）有唯一零点，则2+a＜0或﹣2+a＞0，解得a＜﹣2或a＞2，
即实数a的取值范围是{a|a＜﹣2或a＞2}．
故选：D．
【点评】本题主要考查利用导数研究函数的极值，考查运算求解能力，属于中档题．
8．（4分）若函数在区间（a，a+5）内存在最小值，则实数a的取值范围是（ ）
A．（﹣3，2）B．[﹣3，2）C．[﹣1，2）D．（﹣1，2）
【分析】求导可知一定是在x＝2处取得最小值，由此可建立关于a的不等式组，解出即可．
【解答】解：令f′（x）＝x2﹣2x＝0，解得x＝0或x＝2，在开区间（a，a+5）内的最小值一定是，
又，故，解得﹣1≤a＜2．
故选：C．
【点评】本题考查利用导数研究函数的最值，考查逻辑推理能力，属于基础题．
9．（4分）已知函数f（x）＝x3﹣2x2+x﹣1，则下列说法正确的是（ ）
A．f（x）的极小值为﹣2
B．f（x）的极大值为
C．f（x）在区间上单调递增
D．f（x）在区间（﹣∞，0）上单调递减
【分析】求导得f'（x）＝（x﹣1）（3x﹣1），令f'（x）＝0，解得x＝1或，将f'（x），f（x）随x的变化情况列表，从表中可知f（x）的单调区间和极值情况，求出极大值和极小值，可得答案．
【解答】解：因为f（x）＝x3﹣2x2+x﹣1，所以f'（x）＝3x2﹣4x+1＝（x﹣1）（3x﹣1），
令f'（x）＝0，则x＝1或，
f'（x），f（x）随x的变化情况如下表：
所以f（x）的单调递增区间为（﹣∞，）和（1，+∞），单调递减区间为（，1），故C、D错误；
在x＝处取得极大值；在x＝1处取得极小值﹣1，故B正确，A错误；
故选：B．
【点评】本题考查利用导数研究函数的单调性和极值，掌握函数的单调性与其导函数的正负性之间的关系是解题的关键，考查逻辑推理能力和运算能力，属于中档题．
10．（4分）等比数列{an}满足a1＝32，q＝﹣，记Tn＝a1a2…an（n∈N+），则数列{Tn}（ ）
A．有最大值，有最小值B．有最大值，无最小值
C．无最大值，有最小值D．无最大值，无最小值
【分析】求出等比数列{an}的通项公式an，进而求出Tn，再由数列最大项、最小项的意义判断作答．
【解答】解：依题意，等比数列{an}的通项公式，
，
由知，n∈N*，n≤5时，数列{|Tn|}是递增的，n∈N*，n≥6时，数列{|Tn|}是递减的，
于是得数列{|Tn|}的最大顶为，而n为奇数时，Tn＞0，n偶数时，Tn＜0，
所以和分别是数列{Tn}的最大项和最小项，
所以数列{Tn}有最大值和最小值，
故选：A．
【点评】本题考查了等比数列的性质和最值问题，属于中档题．
11．（4分）已知﹣1，a1，a2，﹣7成等差数列，﹣3，b1，b2，b3，﹣12成等比数列，则b2•（a2﹣2a1）等于（ ）
A．﹣6B．6C．﹣12D．﹣6或6
【分析】设等差数列的公差为d，比数列的公比为q，由题意可得d和q，代入要求的式子化简可得．
【解答】解：设等差数列的公差为d，等比数列的公比为q，
则有﹣1+3d＝﹣7，﹣3•q4＝﹣12，
解之可得d＝﹣2，q2＝2，
∴b2（a2﹣2a1）＝﹣3×2×（﹣5+6）＝﹣6，
故选：A．
【点评】本题考查等比数列和等差数列的性质和应用，属中档题．
12．（4分）函数f（x）＝（x2﹣2x）ex的图象大致是（ ）
A．B．
C．D．
【分析】本题是选择题，可采用排除法进行逐一排除，根据f（0）＝0可知图象经过原点，以及根据导函数大于0时原函数单调递增，求出单调增区间，从而可以进行判定．
【解答】解：因为f（0）＝（02﹣2×0）e0＝0，排除C；
因为f'（x）＝（x2﹣2）ex，解f'（x）＞0，
所以或时f（x）单调递增，排除B，D．
故选：A．
【点评】本题主要考查了利用导数研究函数的单调性，以及函数的图象等基础知识，考查了排除法，属于基础题．
二、填空题。（共4小题，共16分）
13．（4分）过点A（1，1）与曲线C：y＝x3相切的直线方程是 3x﹣y﹣2＝0或3x﹣4y+1＝0 ．
【分析】设切点为（x0，y0），则y0＝x03，由于直线l经过点（1，1），可得切线的斜率，再根据导数的几何意义求出曲线在点x0处的切线斜率，便可建立关于x0的方程．从而可求方程．
【解答】解：若直线与曲线切于点（x0，y0）（x0≠0），则k＝
．∵y′＝3x2，∴y′|x＝x0＝3x02，∴2x02﹣x0﹣1＝0，∴，
∴过点A（1，1）与曲线C：y＝x3相切的直线方程为3x﹣y﹣2＝0或3x﹣4y+1＝0，
故答案为3x﹣y﹣2＝0或3x﹣4y+1＝0
【点评】此题考查学生会利用导数求曲线上过某点切线方程的斜率，会根据一点坐标和斜率写出直线的方程，是一道综合题．
14．（4分）函数f（x）＝x+，设f（x）在区间[1，2]与[3，5]的平均变化率为a，b，则a，b的大小关系为 a＜b ．
【分析】由已知结合函数的平均变化率的定义即可求解．
【解答】解：因为f（x）＝x+，
所以a＝＝＝，b＝＝＝，
则a＜b．
故答案为：a＜b．
【点评】本题主要考查了函数的平均变化率的定义的应用，属于基础题．
15．（4分）已知函数f（x）＝lnx，则＝ ．
【分析】先对函数求导，然后结合导数的定义即可求解．
【解答】解：因为f（x）＝lnx，
所以，
所以＝f′（2）＝．
故答案为：．
【点评】本题主要考查了导数的定义，属于基础题．
16．（4分）若数列{an}满足：a1＝1，an+1＝an+2n，（n∈N+），则数列{an}的通项公式为 2n﹣1 ．
【分析】直接根据递推关系式结合累加法即可求解结论．
【解答】解：∵数列{an}满足：a1＝1，an+1＝an+2n，（n∈N+），
∴an﹣an﹣1＝2n﹣1，
an﹣1﹣an﹣2＝2n﹣2，
an﹣2﹣an﹣3＝2n﹣3，
．
a3﹣a2＝22，
a2﹣a1＝21，
上面各式累加可得：an﹣a1＝2n﹣1+2n﹣2+2n﹣3++21，
∴an＝2n﹣1+2n﹣2+2n﹣3++21+1＝＝2n﹣1，
故答案为：2n﹣1．
【点评】本题主要考查数列递推关系式的应用，考查计算能力和逻辑推理能力，属于基础题．
三、解答题。（共4小题，共36分）
17．（10分）已知等差数列{an}满足：a1＝2，a5＝18．
（1）求数列{an}的通项公式；
（2）记Sn为数列{an}的前n项和，求正整数n的范围，使得Sn＞60n+800．
【分析】（1）根据已知条件，先求出公差，再结合等差数列的通项公式，即可求解．
（2）根据已知条件，求出Sn，令Sn＞60n+800，即可求解．
【解答】解：（1）设等差数列{an}的公差为d，
则4d＝a5﹣a1＝18﹣2＝16，解得d＝4，
故an＝a1+（n﹣1）d＝2+4（n﹣1）＝4n﹣2．
（2），
令2n2＞60n+800，即n2﹣30n﹣400＞0，解得n＞40或n＜﹣10（舍去），
故存在正整数n，使得Sn＞60n+800成立，n的最小值为41．
【点评】本题主要考查等差数列的通项公式，以及等差数列的前n项和公式，属于基础题．
18．（10分）已知函数f（x）＝2x3+3ax2+3bx+1且在x＝1及x＝2处取得极值．
（1）求a，b的值；
（2）求函数y＝f（x）在[0，3]上的最大值与最小值的差．
【分析】（1）求出函数的导数，结合题意得到关于a，b的方程组，解出即可；
（2）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，求出函数的最大值和最小值，作差即可．
【解答】解：（1）∵f（x）＝2x3+3ax2+3bx+1，
∴f′（x）＝6x2+6ax+3b，
∵f（x）在x＝1及x＝2处取得极值，
∴，解得：；
（2）由（1）得：f（x）＝2x3﹣9x2+12x+1，
则f′（x）＝6x2﹣18x+12＝6（x﹣1）（x﹣2），
令f′（x）＞0，解得：x＞2或x＜1，
令f′（x）＜0，解得：1＜x＜2，
故f（x）在（﹣∞，1）递增，在（1，2）递减，在（2，+∞）递增，
故f（x）在[0，1）递增，在（1，2）递减，在（2，3]递增，
故f（x）的最大值是max{f（1），f（3）}＝max{6，10}＝10，
f（x）的最小值是min{f（0），f（2）}＝min{1，5}＝1，
故f（x）的最大值和最小值的差是10﹣1＝9．
【点评】本题考查了函数的单调性，极值，最值问题，考查导数的应用，是中档题．
19．已知函数f（x）＝x2﹣alnx﹣2．
（1）当a＝3时，求f（x）在x＝1处的切线方程；
（2）求f（x）的单调区间．
【分析】（1）由题意得f（x）＝x2﹣3lnx﹣2，求出f'（x）＝x﹣，可得k＝f'（1）＝﹣2，f（1）＝﹣，利用点斜式即可得出答案；
（2）分类讨论a＝0，此时f（x）＝x2﹣2，利用二次函数图象与性质即可得出答案，函数定义域为（0，+∞），f'（x）＝x﹣＝，分类讨论a＜0，a＞0，判断f'（x）的正负，即可得出答案．
【解答】解：（1）由题意得f（x）＝x2﹣3lnx﹣2，f'（x）＝x﹣，
∴k＝f'（1）＝﹣2，f（1）＝﹣，
∴f（x）在点（1，﹣）处的切线方程为y+＝﹣2（x﹣1），即4x+2y﹣1＝0；
（2）当a＝0时，f（x）＝x2﹣2，此时f（x）在（﹣∞，0]上单调递减，在[0，+∞）上单调递增，
函数定义域为（0，+∞），f'（x）＝x﹣＝，
当a＜0时，f'（x）＞0，
当a＞0时，由f'（x）＝0得x＝，由f'（x）＞0得x＞，由f'（x）＜0得0＜x＜，
综上所述，当a＝0时，f（x）的单调递增区间为[0，+∞），单调递减区间为（﹣∞，0]；
当a＜0时，f（x）的单调递增区间为（0，+∞），无递减区间；
当a＞0时，f（x）的单调递增区间为（，+∞），单调递减区间为（0，）．
【点评】本题考查导数的几何意义和利用导数研究函数的单调性，考查转化思想和分类讨论思想，考查逻辑推理能力和运算能力，属于中档题．
20．已知函数f（x）＝lnx﹣ax（a∈R）．
（1）当a＝1时，求函数的单调区间；
（2）若f（x）≤0恒成立，求a的取值范围．
【分析】（1）由题意得f（x）＝lnx﹣x，函数定义域为（0，+∞），求出f'（x）＝，即可得出答案；
（2）由题意得函数定义域为（0，+∞），题意转化为a≥对x∈（0，+∞）上恒成立，构造函数g（x）＝，x∈（0，+∞），求出g'（x），利用导数得出g（x）的单调性和最大值，即可得出答案．
【解答】解：（1）当a＝1时，则f（x）＝lnx﹣x，函数定义域为（0，+∞），则f'（x）＝，
由f'（x）＞0得0＜x＜1，由f'（x）＜0得x＞1，
∴f（x）的单调递增区间为（0，1），单调递减区间为（1，+∞）；
（2）由题意得函数定义域为（0，+∞），
f（x）≤0恒成立，转化为a≥对x∈（0，+∞）上恒成立，
令g（x）＝，x∈（0，+∞），则g'（x）＝，
由g'（x）＝0得x＝e，由g'（x）＞0得0＜x＜e，由g'（x）＜0得x＞e，
∴g（x）在（0，e）上单调递增，在（e，+∞）上单调递减，
∴当x＝e时，g（x）取得极大值也是最大值，g（e）＝，
∴a≥，
故实数a的取值范围为[，+∞）．
【点评】本题考查利用导数研究函数的单调性和导数解决恒成立问题，考查转化思想和函数思想，考查逻辑推理能力和运算能力，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/4/16 13:33:03；用户：笑涵数学；邮箱：15699920825；学号：36906111 x
（﹣∞，）
（，1）
1
（1，+∞）
f'（x）
+
0
﹣
0
+
f（x）
↑
极大值﹣
↓
极小值﹣1
↑