



【期中讲练测】北师大版八年级下册数学压轴真题必刷03 图形的平移与旋转 (压轴专练).zip
展开压轴一:平移的性质压轴二:平移与坐标问题
压轴三:平移几何变换压轴四:中心对称与坐标问题
压轴五:旋转的性质压轴六:旋转与坐标问题
压轴七:旋转线段问题压轴八:旋转面积问题
压轴九:旋转角度问题
【题型归纳】
题型一:平移的性质
1.如图,△ABC中,,把△ABC放在平面直角坐标系xOy中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线上时,线段AC扫过的面积为( )
A.66B.108C.132D.162
【分析】过点C作CD⊥x轴于点D,由点A、B的坐标利用勾股定理可求出点C的坐标,再利用一次函数图象上点的坐标特征可求出点C移动后的坐标,借助平行四边形的面积即可得出线段AC扫过的面积.
【详解】过点C作CD⊥x轴于点D,如图所示.
∵点A,B的坐标分别为(2,0),(12,0),AC=BC=13,
∴AD=BD=AB=5,
∴CD=.
∴点C的坐标为(7,12).
当y=12时,有12=−x+8,
解得:x=−4,
∴点C平移后的坐标为(−4,12).
∴△ABC沿x轴向左平移7−(−4)=11个单位长度,
∴线段AC扫过的面积S=11CD=132.
故选:C.
2.如图,等腰直角三角形△OAB的边OA和矩形OCDE的边OC在x轴上,OA=4,OC=1,OE=2.将矩形OCDE沿x轴正方向平移t(t>0)个单位,所得矩形与△OAB公共部分的面积记为S(t).将S(t)看作t的函数,当自变量t在下列哪个范围取值时,S(t)是t的一次函数( )
A.1<t<2B.2<t<3
C.3<t<4D.1<t<2或4<t<5
D
【分析】分,,,,讨论即可得出结果.
【详解】解:,,,
当矩形在范围内移动时,由0变为2,随的增大而增大,
当矩形在范围内移动时,为定值2,
当矩形在范围内移动时,由2变为0,随的增大而减小,
当矩形在时,为0,
综上所述,矩形在或范围内移动时,是的一次函数,
故选:.
【点睛】本题考查了图形的平移、一次函数的定义,抓住一次函数的定义分类讨论是解决本题的关键.
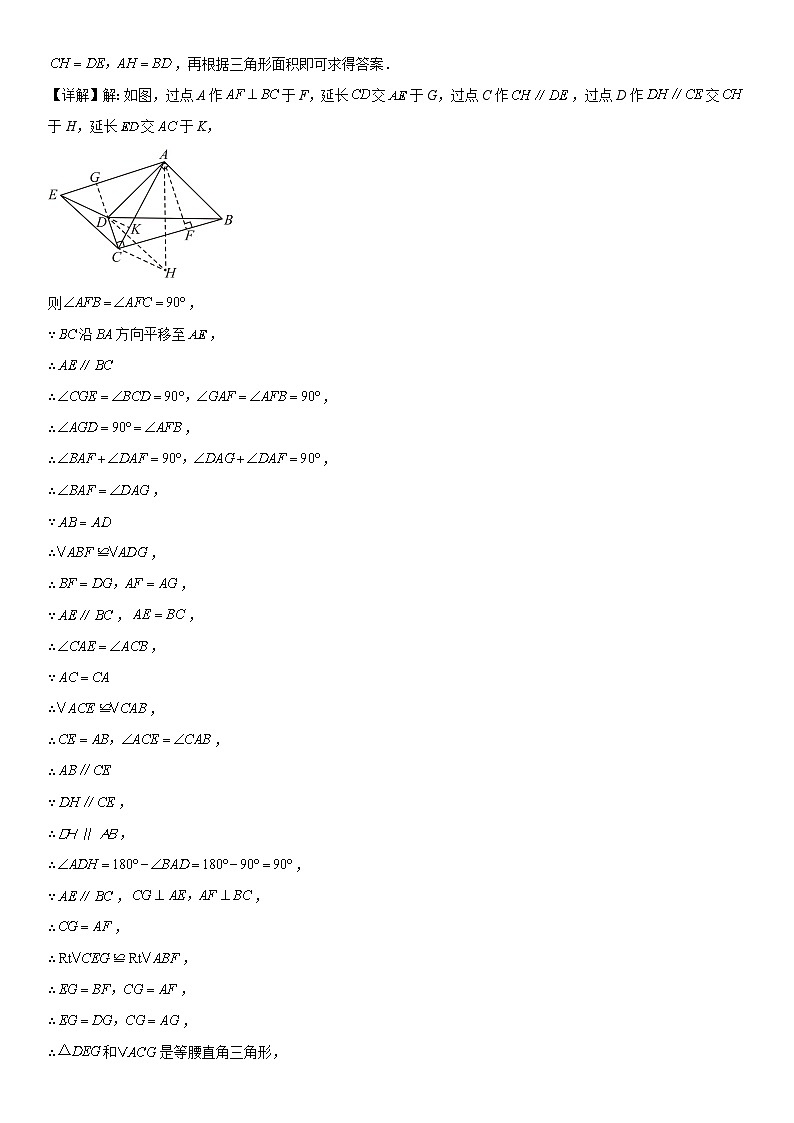
3.如图所示,在四边形中,且,将沿方向平移至,连接,若以和为边构成的三角形面积是,则 .
【分析】如图,过点A作于F,延长交于G,过点C作,过点D作交于H,延长交于K,证明,得出:,再根据三角形面积即可求得答案.
【详解】解:如图,过点A作于F,延长交于G,过点C作,过点D作交于H,延长交于K,
则,
∵沿方向平移至,
∴
∴,
∴,
∴,
∴,
∵
∴,
∴,
∵,,
∴,
∵
∴,
∴,
∴
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴和是等腰直角三角形,
∴,
∴,
∴,
∵,
∴
∵,
∴
∵
∴,
∴,
∴,
∵,
∴,
∴,
∵以和为边构成的三角形面积是,
∴
∴
∴
故答案为:
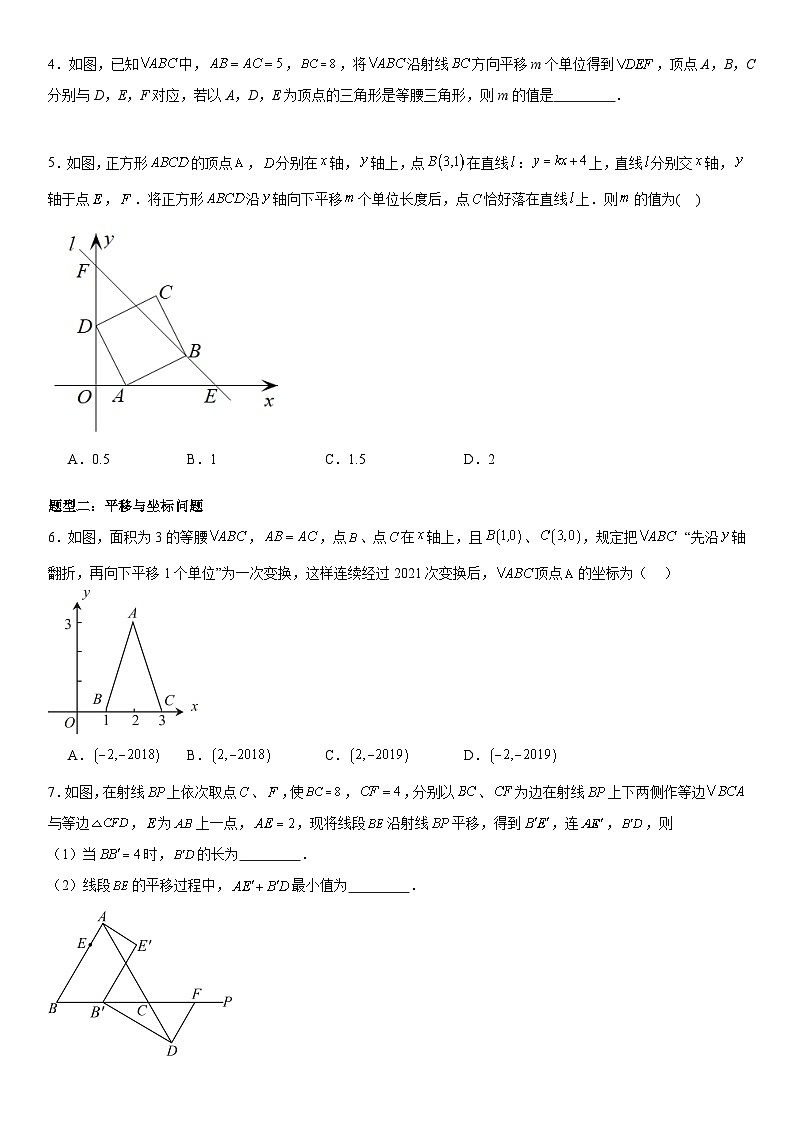
4.如图,已知中,,,将沿射线方向平移m个单位得到,顶点A,B,C分别与D,E,F对应,若以A,D,E为顶点的三角形是等腰三角形,则m的值是 .
【分析】△ADE是等腰三角形,所以可以分3种情况讨论:①当AD=AE时,△ADE是等腰三角形.作AM⊥BC,垂足为M,利用勾股定理列方程可得结论;②当AD=DE时,四边形ABED是菱形,可得m=5;③当AE=DE时,此时C与E重合,m=8.
【详解】解:分3种情况讨论:
①当AD=AE时,如图1,
过A作AM⊥BC于M,
∵AB=AC=5,BM=BC=4,
∴AM=3,
由平移性质可得AD=BE=m,
∴AE=m,EM=4−m,
在Rt△AEM中,由勾股定理得:AE2=AM2+EM2,
∴m2=32+(4−m)2,
m=,
②当DE=AD时,如图2,
由平移的性质得,,
∴四边形ABED是菱形,
∴AD=BE=ED=AB=5,即m=5;
③当AC=DE时,如图3,此时C与E重合,
m=8;
综上所述:当m=或5或8时,△ADE是等腰三角形.
故答案为:或5或8.
5.如图,正方形的顶点,分别在轴,轴上,点在直线:上,直线分别交轴,轴于点,.将正方形沿轴向下平移个单位长度后,点恰好落在直线上.则的值为( )
A.0.5B.1C.1.5D.2
【分析】过B作BM⊥OE于M,过C作CN⊥OF于N,根据AAS定理证得△DAO≌△ABM,△CDN≌△DAO,根据全等三角形的性质求出C点的坐标为(2,3),由待定系数法求出直线l的解析式为y=-x+4,设平移后点C的坐标为(2,3-m),代入解析式即可求出m.
【详解】解:过B作BM⊥OE于M,过C作CN⊥OF于N,如图,
∴∠ABM+∠BAM=90°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=DA,
∴∠DAO+∠BAM=90°,
∴∠DAO=∠ABM,
在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴OA=BM,OD=AM,
∵B(3,1),
∴BM=1,OM=3,
∴OA=1,
∴AM=OM-OA=2,
∴OD=2,
同理可证△CDN≌△DAO,
∴DN=OA=1,CN=DO=2,
∴ON=OD+DN=3,
∴C(2,3),
∵点B(3,1)在直线l:y=kx+4上,
∴3k+4=1,
∴k=-1,
∴直线l的解析式为y=-x+4,
设正方形ABCD沿y轴向下平移m个单位长度后点C的坐标为(2,3-m),
∵点C在直线l上,
∴-2+4=3-m,
解得:m=1,
故选:B.
题型二:平移与坐标问题
6.如图,面积为3的等腰,,点、点在轴上,且、,规定把 “先沿轴翻折,再向下平移1个单位”为一次变换,这样连续经过2021次变换后,顶点的坐标为( )
A.B.C.D.
【分析】根据等腰三角形的面积和B(1,0)、C(3,0);可得A(2,3),然后先求出前几次变换A的坐标,进而可以发现第2021次变换后的三角形在x轴下方,且在第三象限,即可解决问题.
【详解】解:∵面积为3的等腰△ABC,AB=AC,B(1,0)、C(3,0),
∴点A到x轴的距离为3,横坐标为2,
∴A(2,3),
∴第1次变换A的坐标为(-2,2);
第2次变换A的坐标为(2,1);
第3次变换A的坐标为(-2,0);
第4次变换A的坐标为(2,-1);
第5次变换A的坐标为(-2,-2);
∴第2021次变换后的三角形在x轴下方,且第三象限,
∴点A的纵坐标为-2021+3=-2018,横坐标为-2,
所以,连续经过2021次变换后,△ABC顶点A的坐标为(-2,-2018).
故选:A.
7.如图,在射线上依次取点、,使,,分别以、为边在射线上下两侧作等边与等边,为上一点,,现将线段沿射线平移,得到,连,,则
(1)当时,的长为 .
(2)线段的平移过程中,最小值为 .
【分析】(1)根据是等边三角形,,,,可得,是等腰三角形,从而可得是直角三角形,利用勾股定理可得的长;
(2)连接,作交于点,可得四边形和四边形是平行四边形,通过边的转化,可得,即即当D、、G三点共线, 时,的值最小,由证得,可得,在中,利用勾股定理求出的长度,即最小值.
【详解】解:(1),,,
,
是等腰三角形,
是等边三角形,
,
,
,
,
即是直角三角形,
,,
(2)连接,作交于点,
线段沿射线平移,得到,
,
四边形是平行四边形,
,,
四边形是平行四边形,
,
,
要使有最小值,即当D、、G三点共线, 时,的值最小,
,
,
,
,
,
,
,
是等边三角形,
,
,
是等边三角形,
,
,
在中,
即线段的平移过程中,最小值为
8.如图,等边的顶点,,规定把“先沿轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边的顶点的坐标为( )
A.B.
C.D.
【分析】先利用等边三角形的性质求得点C的坐标,然后根据轴对称变换和轴对称变换的性质求得第一次变换,第二次变换,第三次变换后点C的坐标,按此找出规律即可求解 .
【详解】解:如图所示,过点作,
∵△ABC是等边三角形,,,
∴,,轴,D的坐标为(2,1),
∴
∴点C到轴的距离为:,点的横坐标为,
∴,
由题意得,
第一次变换后点的坐标为,即;
第二次变换后点的坐标为,即;
第三次变换后点的坐标为,即;
……
由此可以发现点的横坐标总是比次数大,而纵坐标,当奇次变换时是,偶次变换时是,故连续经过2022次变换后,等边的顶点的坐标为,
故选:
9.在平面直角坐标系中,已知点,,.给出如下定义:若点先向上平移个单位(若,即向下平移个单位),再向右平移3个单位后的对应点Q在的内部或边上,则称点P为的“平移关联点”.若直线上的一点P是的“平移关联点”,且是等腰三角形,则点P的坐标为 .
【分析】本题考查一次函数的综合应用,等腰三角形的性质,坐标与图形,设,根据平移规则,得到,进而得到点在直线上,根据是等腰三角形,分,两种情况讨论,求出点坐标,进而求出点坐标,本题的难度较大,掌握数形结合和分类讨论的思想进行求解,是解题的关键.
【详解】解:∵,,
∴,,
设,则:,
∴点在直线上,
当是等腰三角形,分两种情况:
①当时,过点作,则:,
∵,
∴两点重合,
∴,
∴,
∴,
∴;
②当时,过点作,则:,
∴,
∴,
∴,
∴,
∴,
∴
故答案为:或.
10.对于平面直角坐标系中的不同两点,,给出如下定义:若,,则称点,互为“倒数点”,例如:点,互为“倒数点”.
(1)已知点的坐标为,则点的“倒数点”点的坐标为______;将线段向右平移2个单位得到线段,则线段上______(填“存在”或“不存在”)“倒数点”.
(2)如图,在正方形中,点坐标为,点坐标为,请判断该正方形的边上是否存在“倒数点”,并说明理由.
【分析】(1)设,,由题意得出,,点的坐标为,由平移的性质得出,,即可得出结论;
(2)①若点,在线段上,则,点,应当满足,可知点不在正方形边上,不符题意;
②若点,在线段上,则,点,应当满足,可知点不在正方形边上,不符题意;
③若点,在线段上,则,点,应当满足,得出,,此时点,在线段上,满足题意.
【详解】(1)设,,,,
,,,
,,点的坐标为,
将线段水平向右平移2个单位得到线段,
则,,
,,
线段上不存在“倒数点”,
故答案为:;不存在;
(2)正方形的边上存在“倒数点”、,理由如下:
①若点,在线段上,
则,点,应当满足,
可知点不在正方形边上,不符题意;
②若点,在线段上,
则,点,应当满足,
可知点不在正方形边上,不符题意;
③若点,在线段上,
则,点,应当满足,
点只可能在线段上,,,
此时点,在线段上,满足题意;
该正方形各边上存在“倒数点”,,,.
题型三:平移几何变换
11.如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为,将该三角形沿轴向右平移得到,此时点的坐标为,则线段OA在平移过程中扫过部分的图形面积为 .
【详解】分析:利用平移的性质得出AA′的长,根据等腰直角三角形的性质得到AA′对应的高,再结合平行四边形面积公式求出即可.
详解:∵点B的坐标为(0,2),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2,2),
∴AA′=BB′=2,
∵△OAB是等腰直角三角形,
∴A(,),
∴AA′对应的高,
∴线段OA在平移过程中扫过部分的图形面积为2×=4.
故答案为4.
12.沿等边的高剪开(如图①),再把沿方向向左平移,得到,分别与、相交于点G、E,与相交于点F(如图②),
(1)求证:是等腰三角形.
(2)求证:.
(3)已知厘米,向左平移了2厘米,求的面积.
【分析】(1)根据三线合一证明∠BAD=∠CAD,再由平移可知AD∥A′D′,从而可证明∠A=∠AEG即可;
(2)证明△BFD′≌△CED即可得到结论;
(3)证明△EDC∽△A′D′C,得到,分别算出A′D′,DD′,CD′,即可算出DE,从而可得△CDE的面积.
【详解】解:(1)如图①,∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
则在图②中,∠A=∠A′,
由平移可知:AD∥A′D′,
∴∠A′=∠AEG,
∴∠A=∠AEG,
∴△AGE是等腰三角形;
(2)由图①可知:∠B=∠C,A′D′⊥BC,AD⊥BC,
∵BD=CD′,
∴BD′=CD,
∴△BFD′≌△CED(ASA),
∴BF=CE;
(3)∵AD∥A′D′,
∴△EDC∽△A′D′C,
∴,
∵△ABC是等边三角形,AB=8cm,
∴BD=4cm,
∴A′D′=AD=cm,
∵平移了2cm,
∴DD′=2cm,
∴CD=2cm,
∴,
解得:DE=,
∴△ECD的面积=.
13.如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
【分析】(1)证明DG=GH=EH即可解决问题.
(2)如图2中,作AH⊥BC于H.解直角三角形求出AH,可得OQ的最小值,证明△AOQ≌△COP(ASA),推出AQ=PC,推出y=AQ+AB+BP+PC+PQ=AB+BC+PQ=10+2x(≤x≤4).根据一次函数的性质求出最值即可.
(3)分三种情形:①当AQ=AO=3时,作OH⊥AD于H.②当点Q是AD的中点时.③当OA=OQ=3时,分别求解即可.
【详解】解:(1)如图中,
∵DF=FC,CH∥FG,
∴DG=GH,
∵BC=CE,CH∥BG,
∴GH=HE,
∴DG=GH=HE,
∴DG=DE=AC=2.
(2)如图2中,作AH⊥BC于H.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴OA=OC=3,OB=OD==4,
∴,
∴AH=,
∵AQ∥PC,
∴∠QAO=∠PCO,
∵OA=OC,∠AOQ=∠COP,
∴△AOQ≌△COP(ASA),
∴AQ=PC,
∴y=AQ+AB+BP+PC+PQ=AB+BC+PQ=10+2x(≤x≤4).
∴y=2x+10(≤x≤4).
当x=时,y有最小值,最小值为.
(3)能;
如图3中,
分三种情形:①当AQ=AO=3时,作OH⊥AD于H.
易知OH=,
∴AH==,
∴HQ=,
∴OQ=,
∴PQ=2OQ=.
②当点Q是AD的中点时,AQ=OQ=DQ=,
∴PQ=2OQ=5.
③当OA=OQ=3时,PQ=2OQ=6.
综上所述,满足条件的PQ的值为:或5或6.
14.在平面直角坐标系xOy中,对于点A,规定点A的变换和变换.变换:将点A向左平移一个单位长度,再向上平移两个单位长度;变换:将点A向右平移三个单位长度,再向下平移一个单位长度
(1)若对点B进行变换,得到点(1,1),则对点B进行变换后得到的点的坐标为 .
(2)若对点C(m,0)进行变换得到点P,对点C(m,0)进行变换得到点Q,,求m的值.
(3)点D为y轴的正半轴上的一个定点,对点D进行变换后得到点E,点F为x轴上的一个动点,对点F进行变换之后得到点G,若的最小值为2,直接写出点D的坐标 .
【分析】(1)根据变换求出B的坐标,再根据变换求出对应点的坐标即可;
(2)先求出P、Q的坐标,然后根据OP=OQ构建关于m的方程即可求解;
(3)设D(0,y),F(x,0),则E(-1,y+2),G(x+3,-1),可得
=,令(-3,y+1), (-1,y+2),则,,推出,推出的最小值就是x轴上点F(x,0)到, 的距离之和的值最小.
【详解】(1)解:由题意知:点(1,1)向右平移一个单位长度,再向下平移两个单位长度即可得到B,
∴B的坐标为(2,-1),
∴点B进行变换后得到的点的坐标为(5,-2);
故答案为:(5,-2);
(2)解:由题意知:对点C(m,0)进行变换得到点P的坐标为(m-1,2),对点C(m,0)进行变换得到点Q(m+3,-1),
∵OP=OQ,
∴,即,
∴;
(3)解:由题意,设D(0,y),F(x,0),则E(-1,y+2),G(x+3,-1),
∴,,
∴
=
令(-3,y+1), (-1,y+2),
则,
∴,
∴的最小值就是x轴上点F(x,0)到, 的距离之和的值最小,
如果, 在x轴的两侧,那么点F就是与x轴的交点,的最小值就是的长,
此时,故此种情况不符合题意,舍去,
如果, 在x轴的同侧,作关于x轴的对称点(-3,-y-1),连接交x轴于点K,此时,的值最小,
∴,
∴或,
又点D(0,y)在y轴上,则y>0,
∴,
∴D的坐标为(0,).
故答案为:(0,).
15.平面直角坐标系中,正方形的四个顶点坐标分别为:,,,,、是这个正方形外两点,且给出如下定义:记线段的中点为,平移线段得到线段其中,分别是点,的对应点,记线段的中点为若点和分别落在正方形的一组邻边上,或线段与正方形的一边重合,则称线段长度的最小值为线段到正方形的“回归距离”,称此时的点为线段到正方形的“回归点”.
(1)如图,平移线段,得到正方形内两条长度为的线段和,这两条线段的位置关系为______;若,分别为和的中点,则点______填或为线段到正方形的“回归点”;
(2)若线段的中点的坐标为,记线段到正方形的“回归距离”为,请直接写出的最小值:______,并在图中画出此时线段到正方形的“回归点”画出一种情况即可;
(3)请在图中画出所有符合题意的线段到正方形的“回归点”组成的图形.
【分析】(1)利用平移变换的性质以及“回归点”的定义判断即可;
(2)如图当与的中点重合或与的中点重合时,的值最小,再利用勾股定理求解;
(3)分点和分别落在正方形的一组邻边上,或线段与正方形的一边重合两种情况取最小值即可.
【详解】(1)如图,平移线段,得到正方形内两条长度为的线段和,这两条线段的位置关系为;若分别为和的中点,则点为线段到正方形的“回归点”.
故答案为:,;
(2)如图当与的中点重合或与的中点重合时,的值最小,最小值;
故答案为:;
;
(3)由题意可知正方形边长为1,
当线段与正方形的一边重合时,
∵,
∴线段即正方形任意一边,
∵T在第一象限,
由“回归点”定义可知不合题意,
故此时“回归点”在E,F处,
如图,
;
当点和分别落在正方形的一组邻边上时,当线段PQ向右倾斜时,点的的边应在第二、四象限.且低的度小于45度时, 点在第四象限时比在二象限时短,因此回归点在第四象限;当倾斜度大于45度时,点在第二象限时比在四象限时短,因此回归点在第二象限.如图:
;
综上所述,“回归点”组成的图形如图所示,
.
题型四:中心对称与坐标问题
16.如图,分别在四边形的各边上取中点,,,,连接,在上取一点,连接,过作,交于,将四边形中的四边形①和②移动后按图中方式摆放,得到四边形和,延长,相交于点,得到四边形.下列说法中正确的是( )
①②③④四边形是平行四边形
A.①②③B.①③④C.①②④D.②③④
16.B
【分析】顺次连接,连接交于点,得,于是,证明,即可判断①;由对称性可得:,则,由,即可判定四边形是平行四边形,即可判断④;四边形是平行四边形,则,无法证明,即可判断②;四边形四边形,四边形四边形,四边形四边形,得到,则,即可判断③.
【详解】解:如图,
顺次连接,连接,连接交于点,
∵分别在四边形的各边上取中点,,,,
∴,
∴,
∴四边形是平行四边形,
∴,
,
∵,
∴,
∴,
∴,
故①正确;
由对称性可得:,
,
,
四边形是平行四边形,
故④正确;
四边形是平行四边形,
,
无法证明,
故②不正确;
依题意,四边形四边形,四边形四边形,
由题意得,四边形是由移动得到的,
∵,
∴四边形可以看成是四边形以点H为旋转中心,逆(顺)时针旋转得到的,
∴,
即在同一条直线上,,,
∴,
又∵四边形是由四边形移动后得到的,
∴,,
∵,
∴,
同理可得,,,
∵,,
∴四边形四边形,
,
∴,
故③正确;
故答案为:B.
17.如图,这是小聪设计的正方形花边图案,该图案由正方形和三角形拼接组成(不重叠,无缝隙),它既是轴对称图形,又是中心对称图形.若图中阴影面积的和为36,则图中线段的长为 .
【分析】把图形局部放大如图所示:作于N,于M,连接交于P交于Q,延长交于H,设,则.由,,推出,,,设,由,可得,推出,根据,构建方程求出a即可解决问题.
【详解】解:把图形局部放大如图所示,作于N,于M,连接交于P交于Q,延长交于H,设,则.
由题意得:是等腰直角三角形,,
∴,
∵,
∴,
同理,
∴,,,
设,
∵,
∴,
∴,
∵,
∴,
解得或(舍弃),
∴,
故答案为.
18.如图,在中,,,的面积为,动点从点出发,以个单位长度的速度沿线段向终点运动,同时动点从点出发以个单位长度的速度在间往返运动,当点到达点时,动点、同时停止运动,连接设运动时间为秒.
(1)则和之间的距离为 ;
(2)当平分的面积时,则 .
【分析】(1)根据平行四边形的面积公式即可求解;
(2)由平分的面积可得是中心对称图形,所以,分三种情况求解.
【详解】(1)设和之间的距离为,
,的面积为,
,
,
和之间的距离为.
故答案为:.
(2)平分的面积,是中心对称图形,
经过的中心,
,
当时,
,,
,
;
当时,
,,
,
;
当时,
,,
,
.
当平分的面积时,或或.
故答案为:或或
19.已知在中,,,.点为边上的动点,点F为边上的动点,则线段的最小值是 .
【分析】作F点关于AC的对称点,连接A并延长交BC延长线于点,将的最小值转化为求B点到A 的最短距离,根据垂线段的性质即可解答;
【详解】解:如图作F点关于AC的对称点,连接A 并延长交BC延长线于点B′,作BD⊥AB′于点D,
由对称性可得EF=E ,
由垂线段的性质可得B到AB′的最短距离为BD,
∴EF+EB=E+EB=B≥BD,
Rt△ABC中,∠BAC=90°-∠ABC=15°,
∴∠BAD=2∠BAC=30°,
Rt△ABD中,AB=5,∠BDA=90°,∠BAD=30°,∴BD=,
∴线段的最小值是,
故答案为:;
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(1,1).
(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,画出△ABC关于原点O对称的△A2B2C2,并写出点B2的坐标____________;
(3)请在x轴上找一点D得到▱ACDB,则点D的坐标为________,若直线y=x+b平分▱ACDB的面积,则b=_______.
【分析】(1)分别作出点A、B以C为中心,顺时针旋转90°后的对应点A1、B1即可解答;
(2)根据中心对称的坐标特征:横纵坐标互为相反数;求得A2、B2、C2的坐标即可;
(3)C点先向下平移1个单位,再向右平移2个单位,即可得到点D(3,0);求出平行四边形ACDB的中心坐标,根据中心对称图形的性质可得直线y经过中心坐标,进而求得b;
【详解】(1)解:如图,分别作出点A、B以C为中心,顺时针旋转90°后的对应点A1、B1,
连接相应顶点得△A1B1C即为所求;
(2)解:∵A(3,3),B(5,2),C(1,1),
∴A、B、C关于原点的对称点坐标为:A2(-3,-3),B2(-5,-2),C2(-1,-1),
如图,△A2B2C2即为所求,
(3)解:如图,C点先向下平移1个单位,再向右平移2个单位,得到点D(3,0),连接相应顶点,四边形ACDB为平行四边形;
∵A点先向下平移1个单位,再向右平移2个单位,可得到点B,
∴BD可由AB平移得到,即BD∥AB,BD=AB,
∴四边形ACDB是平行四边形,
∵C(1,1),B(5,2),平行四边形是中心对称图形,
∴平行四边形ACDB的中心坐标为(3,),
如图所示,当直线y经过平行四边形中心时,直线两侧的图形关于中心点对称面积相等,
∴(3,)代入直线y=x+b,可得b=6;
题型五:旋转的性质
21.如图,在中,,,O为的中点,将绕点O顺时针旋转得到,D、E分别在边和的延长线上,连接,若则的面积是( )
A.B.C.D.
【分析】连接,根据等腰三角形的性质可得,,,根据旋转的性质可得,由此得是等边三角形,,则,根据勾股定理和三角形面积公式即可求出的面积.
【详解】解:连接,
,,O为的中点,
,,,
∵将绕点O顺时针旋转得到,
,
是等边三角形,,
,
,
,
,
是等边三角形,
,
垂直平分,
,
,
,
,
.
故选:D
22.如图,是等边三角形内一点,且,,,以下4个结论:①;②;③;④若点到三边的距离分别为,,.则有,其中正确的有( )
A.4个B.3个C.2个D.1个
【分析】将绕点逆时针旋转到,得到是等边三角形,根据,得到直角三角形,且,,,从而得到;,;根据勾股定理,,根据等边三角形面积等于得到,利用同一图形的面积不变性,,选择即可.
【详解】如图,将绕点逆时针旋转到,
是等边三角形,,
,,
,
是直角三角形,且,,
;,
;
故①②都正确;
根据勾股定理,得,
如图,作于点,
是等边三角形,
,
,
故③正确;
,
,
,
,
,
故④正确,
故选A.
23.如图,点为正方形内一点,,将绕点按顺时针旋转,得到. 延长交于点,连接,下列结论:①,②四边形是正方形,③若,则;其中正确的结论是( )
A.①②③B.①②C.②③D.①③
【分析】设交于,由及将绕点按顺时针方向旋转,得到,可得,即可得,从而判断①正确;由旋转的性质可得,,,由正方形的判定可证四边形是正方形,可判断②正确;过点作于,由等腰三角形的性质可得,,由“”可得,可得,由旋转的性质可得,从而可得,判断③正确.
【详解】解:设交于,如图:
四边形是正方形,
,
,
将绕点按顺时针方向旋转,得到,
,
,
,
,
,故①正确;
将绕点按顺时针方向旋转,
,,,
又,
四边形是矩形,
又,
四边形是正方形,故②正确;
如图,过点作于,
,,
,
,
四边形是正方形,
,,
,
,
又,,
,
,
将绕点按顺时针方向旋转,
,
四边形是正方形,
,
,
,故③正确;
正确的有:①②③,
故选:A.
24.如图,等边三角形的边长为2,点是的中心(三角形三条中垂线的交点),,绕点旋转分别交线段,于,两点,连接,给出下列四个结论:
;②;③四边形的面积始终等于;④△BDE周长的最小值为是.上述结论中正确的个数是( ).
A.1B.2C.3D.4
【详解】解:连接、,如图,
为等边三角形,
,
点是的中心,
,、分别平分和,
,即,
而,即,
,且,,
,
,,所以①正确;
,所以②正确;
,
四边形的面积,所以③正确;
作于,如图,则,
,
,
,,
,
,
的周长,
当时,最小,的周长最小,此时,
周长的最小值,
④错误.
故选:C.
25.如图,O是等边内一点,,将线段以点B为旋转中心逆时针旋转得到线段,下列结论:
①可以由绕点B逆时针旋转得到;②点O与的距离为4;
③;④;⑤.其中结论正确的是( )
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
【详解】解:连接,过点O作,垂足为D,
由旋转得:,,
∵是等边三角形,
∴,
∴,
∴,
∴,
∴可以由绕点B逆时针旋转得到,故①正确;
由旋转得:,
∴是等边三角形,
∴,
∴点O与的距离为4,故②正确;
∵是等边三角形,
∴,
∵,
∴,
∴,
∴是直角三角形,
∴,
∴,故③正确;
在中,,
∴
,故④不正确;
将绕点A逆时针旋转,使得与重合,点O旋转至点的位置,连接,过点A作,垂足为F,如图:
由旋转得:,
∴是等边三角形,
∴,
∵,
∴,
∴是直角三角形,
在中,,
∴
,
故⑤不正确;
所以,上列结论,正确的结论是①②③,
故选:D.
题型六:旋转与坐标问题
26.如图,点P为直线上一点,先将点P向左移动2个单位,再绕原点O顺时针旋转后,它的对应点Q恰好落在直线上,则点Q的横坐标为( )
A.B.C.D.
【详解】∵点P为直线上一点,
∴点P向左移动2个单位后的解析式为,
∵绕原点O顺时针旋转后解析式为
∴,可得,
∴点Q的横坐标为.
故选:B
【点睛】此题考查一次函数,解题关键是将点的平移和旋转转化为函数平移和旋转,然后求函数的交点坐标.
27.如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2021次,点B的落点依次为B1,B2,B3,……,则B2021的坐标为( )
A.(1010,0)B.(1345,)C.(,)D.(1346,0)
【详解】
解:如图,连接,
∵四边形是菱形,
∴,
∵,
∴是等边三角形,
∴,
∴,
∵,
∴,
画出第5次,第6次,第7次,翻转后的图形,
由图可知,每翻转6次,图形向右平移4个单位长度,
∵2021=336×6+5,
∴点向右平移1344(即336×4)个单位长度到点,
∵点的坐标为,
∴点的坐标为,
∴点坐标为,
故选:C.
28.如图所示,在平面直角坐标系中,,,是等腰直角三角形,且,把绕点顺时针旋转,得到;把绕点顺时针旋转,得到.依次类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点的坐标为( )
A.B.C.D.
【详解】解:过作轴于点,如图:
∵,
∴
∵是等腰直角三角形
∴,
∴的纵坐标为,横坐标为
∵把绕点顺时针旋转,得到;把绕点顺时针旋转,得到
∴的纵坐标为,的纵坐标为, 的纵坐标为,的纵坐标为,;的横坐标为,的横坐标为,的横坐标为,的横坐标为
∴的纵坐标为,的横坐标为,即.
故选:A
29.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转后得到正方形,依此方式,绕点O连续旋转2019次得到正方形,那么点的坐标是( )
A.B.C.D.
【详解】四边形OABC是正方形,且,
,
将正方形OABC绕点O顺时针旋转后得到正方形,
∴点A1的横坐标为1,点A1的纵坐标为1,
,
继续旋转则,,A4(0,-1),A5,A6(-1,0),A7,A8(0,1),A9,……,
发现是8次一循环,所以…余3,
点的坐标为,
故选A.
【详解】四边形OABC是正方形,且,
,
将正方形OABC绕点O顺时针旋转后得到正方形,
∴点A1的横坐标为1,点A1的纵坐标为1,
,
继续旋转则,,A4(0,-1),A5,A6(-1,0),A7,A8(0,1),A9,……,
发现是8次一循环,所以…余3,
点的坐标为,
故选A.
题型七:旋转线段问题
30.如图1,在中,,,D,E分别为边和的中点,将绕点A自由旋转,如图2,直线与相交于点P.
(1)在图1中,线段与的数量关系是 ,位置关系是 ;
(2)对于图2,(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)当时,请直接写出线段的长.
【详解】(1)解:,D,E分别为边和的中点,
,
,即,
,
,
故答案为:,;
(2)证明:(1)中的结论仍然成立,理由如下,
∵,都是等腰直角三角形,
,,,
,
在和中,
,
,
,,
,
,
;
(3)解:由(2)知,
,,
,
,
,
,
,
四边形为正方形,
,
,D,E分别为边和的中点,
,
,
在中,,
,
.
31.通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形的边上,,连接,试猜想之间的数量关系
(1)思路梳理:
把绕点A逆时针旋转至,可使与重合,由,得,,即点F、D、G共线,易证_________,故之间的数量关系为_________.
(2)类比引申:
如图2,点E、F分别在正方形的边的延长线上,.连接,试猜想之间的数量关系为_________,并给出证明.
(3)联想拓展:
如图3,在中,,点D、E均在边上,且.若,直接写出和的长.
【详解】(1)解:如图1,把绕点逆时针旋转至,可使与重合,即,
由旋转得:,,,,
,
即点、、共线,
四边形为矩形,
,
,
,
,
,
在和中,
,
,
,
;
故答案为:,;
(2)如图2,,理由是:
把绕点逆时针旋转至,可使与重合,则在上,
由旋转得:,,,
,
,
,
,
,
在和中,
,
,
,
;
(3)如图3,把绕点逆时针旋转至,可使与重合,连接,,
由旋转得:,,,
,,
,
,
,
,,
由勾股定理得:,
,,
,
,
,
,
,
,
,
,
.
,
,
,
,
过A作,垂足为,
∵,,
∴,
∴,
∴.
题型八:旋转面积问题
32.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是 ,∠MNP的大小为 ;
(2)探究证明:把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由;
(3)拓展延伸:当∠BAC=90°,AB=AC=10,AD=AE=6时,把△ADE绕点A在平面内自由旋转,如图3,请求出△MNP面积的最大值.
【详解】(1)解:∵AB=AC,AD=AE,
∴BD=CE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥AB,PN∥AC,
∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,
∴∠MNE+∠ENP=∠ABE+∠AEB,
∵∠ABE+∠AEB=180°−∠BAE=60°,
∴∠MNP=60°,
故答案为:MN=NP,∠MNP=60°.
(2)△MNP是等边三角形,理由如下:
由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥BD,PN∥CE,
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,
∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB,
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,
∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC−∠ECB=180°−∠BAC=60°,
∴△MNP是等边三角形;
(3)由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MP=EC,PN=BD,MP∥EC,PN∥BD,
∴MP=PN,∠ACE=∠ABD,∠MPD=∠ECD,∠PNC=∠DBC,
∴∠MPD=∠ECA+∠ACD=∠ABD+∠ACD,
∠DPN=∠PCB+∠PNC=∠PCB+∠DBC,
∴∠MPN=∠MPD+∠DPN=∠ABD+∠ACD+∠PCB+∠DBC=∠ABC+∠ACB=180°−∠BAC=90°,
∴△MPN是等腰直角三角形,
由三角形三边关系可知:BD≤AB+AD,
即BD≤16,
PM=,
∴PM=8时,S△MNP最大,
∴S△MNP最大为:×8×8=32.
33.如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.
(1)观察猜想:图1中,线段与的数量关系是______,位置关系是______;
(2)探究证明:把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点在平面内自由旋转,若,,请直接写出面积的最大值______.
【详解】(1)解:点N,分别是,的中点,
,,
点,是,的中点,
,,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:,;
(2)是等腰直角三角形.理由如下:
由旋转知,,
,,
,
,,
利用三角形的中位线得,,,
,
是等腰三角形,
同(1)的方法得,,
,
同(1)的方法得,,
,
,
,
,
,
,
是等腰直角三角形;
(3)由(2)知,是等腰直角三角形,,
最大时,面积最大,
点在的延长线上时,BD最大,
,
,
故答案为:8
题型九:旋转角度问题
34.如图与为正三角形,点O为射线上的动点,作射线与直线相交于点E,将射线绕点O逆时针旋转,得到射线,射线与直线相交于点F.
(1)如图①,点O与点A重合时,点E,F分别在线段,上,求证:;
(2)如图②,当点O在的延长线上时,E,F分别在线段的延长线和线段的延长线上,三条线段之间的数量关系;
(3)点O在线段上,若,当时,请直接写出的长.
【详解】(1)证明:如图①中,
∵与为正三角形,
∴,,
∵将射线绕点O逆时针旋转,
,
,
,
,,
;
(2)解:,理由如下:,
如图②,过点O作交与点H,
,
,
是等边三角形,
,
,
,
,
,
,
,
,
,
,
;
(3)解:作于H.
,为正三角形,,
,
,
如图③中,当点O在线段上,点E在线段上时.
,
,
,
过点O作,交于N,
是等边三角形,
,
,
,
,
,
,
,
,
,
,
;
如图③﹣2中,当点O在线段上,点E在线段上,点F在线段的延长线上时,
同法可证:,
,
;
如图③﹣3中,当点O在线段上,点F在线段上,点E在线段上时.
同法可证:,
,
,
;
如图③中,当点O在线段上,点F在线段的延长线上,点E在线段上时.
同法可知:,
而,
,
;
综上所述,满足条件的的值为4或2或6.
35.问题:如图(1),在中,,,,试探究满足的等量关系.
[探究发现]
小明同学利用图形变换,将绕点C逆时针旋转得到,连接,由已知条件易得,,根据“边角边”可证 ,得,在中,由 定理,可得,得,可得之间的等量关系是 .
[实验运用]
(1)如图2,在正方形中,的顶点E、F分别在边上,高与正方形的边长相等,求的度数.
(2)在(1)条件下,连接,分别交于点M、N,若,运用小明同学探究的结论,求正方形边长以及的长.
解:绕点C逆时针旋转得到,
,
,,,
,
,
即,
,
,
在与中,
,
,
,
在中,由勾股定理,可得,
.
[实验运用]:
(1)解:高与正方形的边长相等,
,,,
在直角与直角中,
,
,
,
同理可得,
,
;
(2)由(1)得,
设正方形的边长为x,则,,
根据勾股定理,可得,
解得或(舍去)
正方形的边长为6,
根据[探究发现]中的结论,可得,
设,则 ,
可列方程,
解得,
.
【期中讲练测】苏科版八年级下册数学 06期中必刷题(压轴专练).zip: 这是一份【期中讲练测】苏科版八年级下册数学 06期中必刷题(压轴专练).zip,文件包含期中讲练测苏科版八年级下册数学06期中必刷题压轴专练解析版docx、期中讲练测苏科版八年级下册数学06期中必刷题压轴专练原题版docx等2份试卷配套教学资源,其中试卷共143页, 欢迎下载使用。
【期中讲练测】苏科版八年级下册数学 05期中必刷题(强化专练).zip: 这是一份【期中讲练测】苏科版八年级下册数学 05期中必刷题(强化专练).zip,文件包含期中讲练测苏科版八年级下册数学05期中必刷题强化专练解析版docx、期中讲练测苏科版八年级下册数学05期中必刷题强化专练原题版docx等2份试卷配套教学资源,其中试卷共108页, 欢迎下载使用。
【期中讲练测】苏科版八年级下册数学 04期中必刷题(易错专练).zip: 这是一份【期中讲练测】苏科版八年级下册数学 04期中必刷题(易错专练).zip,文件包含期中讲练测苏科版八年级下册数学04期中必刷题易错专练解析版docx、期中讲练测苏科版八年级下册数学04期中必刷题易错专练原题版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。












