江苏省南京市浦口区浦口区星甸中学2023-2024学年九年级下学期3月月考数学试题（原卷版+解析版）

这是一份江苏省南京市浦口区浦口区星甸中学2023-2024学年九年级下学期3月月考数学试题（原卷版+解析版），文件包含江苏省南京市浦口区浦口区星甸中学2023-2024学年九年级下学期3月月考数学试题原卷版docx、江苏省南京市浦口区浦口区星甸中学2023-2024学年九年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
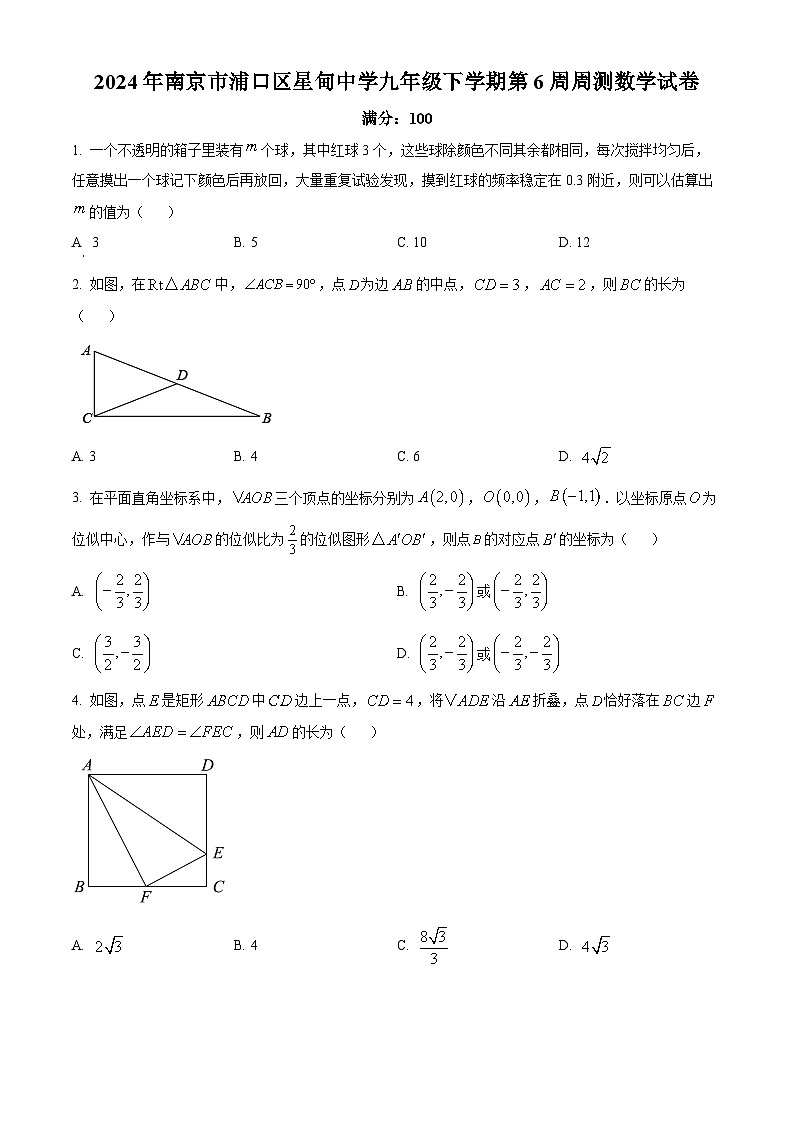
1. 一个不透明的箱子里装有个球，其中红球3个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.3附近，则可以估算出的值为（ ）
A. 3B. 5C. 10D. 12
【答案】C
【解析】
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，根据红球的个数除以总数等于频率，求解即可．
【详解】解：∵大量重复试验后发现，摸到红球的频率在0.3，
∴任意摸出一个球，摸到红球的概率为0.3，
∴，
∴，
经检验是原方程的解．
故选：C．
【点睛】此题主要考查了利用频率估计概率，解分式方程，解答此题的关键是利用红球的个数除以总数等于频率．
2. 如图，在中，，点为边的中点，，，则的长为（ ）
A. 3B. 4C. 6D.
【答案】D
【解析】
【分析】根据直角三角形斜边中线的性质，推导得，再根据勾股定理性质计算，即可得到答案．
【详解】∵，点为边的中点，，
∴，
∴，
故选：D ．
【点睛】本题考查了直角三角形斜边中线、勾股定理的知识；解题的关键是熟练掌握勾股定理的性质，从而完成求解．
3. 在平面直角坐标系中，三个顶点的坐标分别为，，．以坐标原点为位似中心，作与的位似比为的位似图形，则点的对应点的坐标为（ ）
A. B. 或
C. D. 或
【答案】B
【解析】
【分析】根据位似图形的定义可知，位似比为，将点的横坐标分别乘以或即可求解．
【详解】解：将点的横坐标分别乘以或，
∴的坐标是或，
故选：．
【点睛】本题主要考查位似，掌握位似的性质是解题的关键．
4. 如图，点是矩形中边上一点，，将沿折叠，点恰好落在边处，满足，则的长为（ ）
A. B. 4C. D.
【答案】C
【解析】
【分析】根据矩形和轴对称的性质，得，,，根据含角直角三角形的性质，得，，从而推导得，再根据勾股定理性质计算，即可得到答案.
【详解】∵点是矩形中边上一点，将沿折叠，点恰好落在边处，
∴，,
∵
∴
∵
∴
∴
∴，
设，则
∴
∴，即
∴
∴
故选：C.
【点睛】本题考查了含角直角三角形、矩形、轴对称、勾股定理的知识；解题的关键是熟练掌握含角直角三角形、矩形的性质，从而完成求解.
5. 在反比例函数（为常数）的图象上有三个点，，，则函数值，，的大小关系为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】先根据反比例函数的解析式中，判断出函数图像所在的象限及增减性，再根据各点横坐标的特点即可得出结论．
【详解】解：∵，
∴反比例函数的图像位于第二、四象限，
∵，位于第二象限，且，
∴，
∵位于第四象象，
∴，
∴，
故选：D．
【点睛】本题主要考查反比例函数图像上点的坐标特征，解题关键在于通过判断以确定函数图像所在的象限及增减性．
6. 如图，在中，，M是AB的中点，点D在BM上，，，垂足分别为E、F，连接EM，则下列结论中：①；②；③；④，其中正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
【答案】D
【解析】
【分析】证明△BCF≌△CAE，得到BF=CE，可判断①；再证明△BFM≌△CEM，从而判断△EMF为等腰直角三角形，得到∠MEF=∠MFE=45°，可判断②；证明△CDM∽ADE，得到对应边成比例，结合BM=CM，AE=CF，可判断③；证明△DFM≌△NEM，得到△DMN为等腰直角三角形，得到DN=DM，可判断④．
【详解】解：∵∠ACB=90°，
∴∠BCF+∠ACE=90°，
∵∠BCF+∠CBF=90°，
∴∠ACE=∠CBF，
又∵∠BFC=90°=∠AEC，AC=BC，
∴△BCF≌△CAE（AAS），
∴BF=CE，故①正确；
由全等可得：AE=CF，BF=CE，
∴AE-CE=CF-CE=EF，
如图，连接FM，CM，
∵点M是AB中点，
∴CM=AB=BM=AM，CM⊥AB，
在△BDF和△CDM中，∠BFD=∠CMD，∠BDF=∠CDM，
∴∠DBF=∠DCM，
又BM=CM，BF=CE，
∴△BFM≌△CEM（SAS），
∴FM=EM，∠BMF=∠CME，
∵∠BMC=90°，
∴∠EMF=90°，即△EMF为等腰直角三角形，
∴∠MEF=∠MFE=45°，
∵∠AEC=90°，
∴∠MEF=∠AEM=45°，故②正确，
∵∠CDM=∠ADE，∠CMD=∠AED=90°，
∴△CDM∽△ADE，
∴，
∵BM=CM，AE=CF，
∴，
∴CF•DM=BM•DE，故③正确；
如图，设AE与CM交于点N，连接DN，
∵∠DMF=∠NME，FM=EM，∠DFM=∠DEM=∠AEM=45°，
∴△DFM≌△NEM（ASA），
∴DF=EN，DM=MN，
∴△DMN为等腰直角三角形，
∴DN=DM，而∠DEA=90°，
∴DE2+DF2=DN2=2DM2，故④正确；
故正确结论为：①②③④．共4个．
故选：D．
【点睛】本题属于三角形综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，等腰直角三角形的判定和性质，等量代换，难度较大，解题的关键是添加辅助线，构造全等三角形．
7. 如图，，，E，F分别为线段和射线上的一点，若点E从点B出发向点A运动，同时点F从点B出发沿射线运动，二者速度之比为3∶7，当点E运动到点A时，两点同时停止运动．在射线AC上取一点G，使与全等，则的长为_____．
【答案】18或70##70或18
【解析】
【分析】设，则，使与全等，由可知，分两种情况：当时，当时，列方程即可求解．
【详解】解：设，则，因为，使与全等，可分两种情况：
情况一：当时，
∵，
∴，
解得：，
∴；
情况二：当时，
∵，
∴，
解得：，
∴，
综上所述，或70．
故答案为：18或70．
【点睛】本题主要考查了全等三角形的性质，利用分类讨论思想是解答此题的关键．
8. 若是一个完全平方式，则的值为_________．
【答案】
【解析】
【分析】这里首末两项是和4这两个数的平方，那么中间一项为加上或减去和4积的2倍．
【详解】解：∵是一个完全平方式，
∴，
则．
故答案为：．
【点睛】此题主要考查了完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．
9. 已知二次函数图像如图所示．将此函数图像向右平移3个单位得抛物线的图像，则阴影部分的面积为____________．
【答案】15
【解析】
【分析】根据题意知阴影部分面积等于平行四边形面积，由平行四边形的面积公式可得到阴影部分的面积．
【详解】解：由题意知，，则顶点坐标是．
所以，阴影部分的面积为：3×5=15．
故答案是：15．
【点睛】本题考查了二次函数图象与几何变换，图形的面积，要求熟练掌握平移的规律：左加右减，上加下减．
10. 若为二次函数的图像上的三点，则的大小关系是____________．（用“