专题07 反比例函数K值与几何面积综合-备战中考数学一轮复习考点帮（全国通用）

这是一份专题07 反比例函数K值与几何面积综合-备战中考数学一轮复习考点帮（全国通用），文件包含专题07反比例函数K值与几何面积综合-备战中考数学一轮复习考点帮全国通用原卷版docx、专题07反比例函数K值与几何面积综合全国通用解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
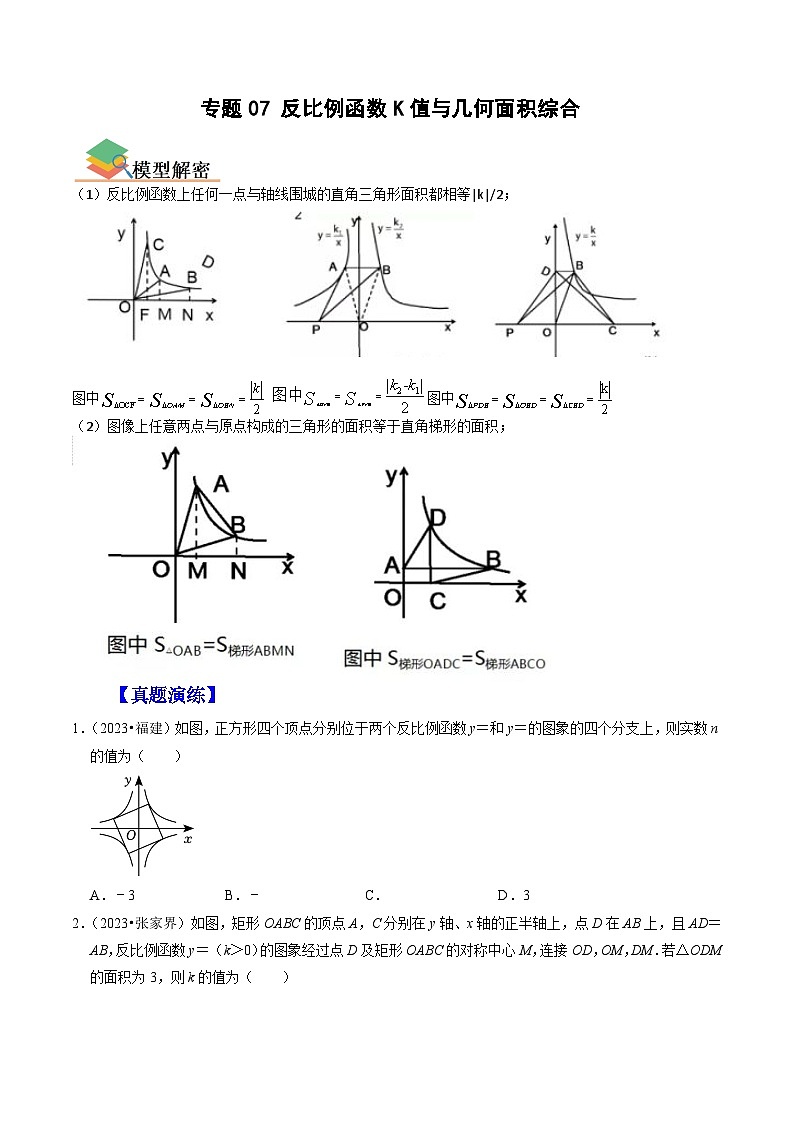
（1）反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2；

（2）图像上任意两点与原点构成的三角形的面积等于直角梯形的面积；
【真题演练】
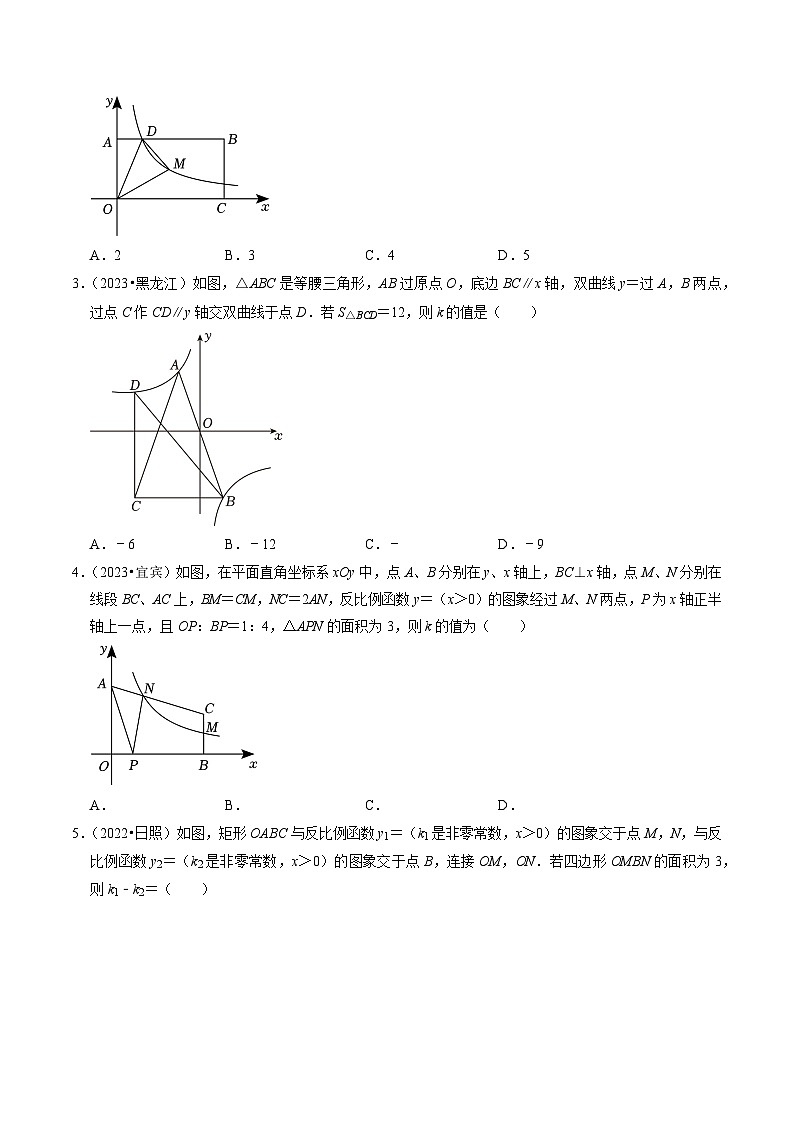
1．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y＝和y＝的图象的四个分支上，则实数n的值为（ ）
A．﹣3B．﹣C．D．3
【答案】A
【解答】解：连接正方形的对角线，由正方形的性质知对角线交于原点O，过点A，B分别作x轴的垂线．垂足分别为C、D，点B在函数y＝上，如图：
∵四边形是正方形，
∴AO＝BO，∠AOB＝∠BDO＝∠ACO＝90°，
∴∠CAO＝90°﹣∠AOC＝∠BOD，
∴△AOC≌△BOD（AAS），
∴S△AOC＝S△OBD＝＝，
∵点A在第二象限，
∴n＝﹣3，
故选：A．
2．（2023•张家界）如图，矩形OABC的顶点A，C分别在y轴、x轴的正半轴上，点D在AB上，且AD＝AB，反比例函数y＝（k＞0）的图象经过点D及矩形OABC的对称中心M，连接OD，OM，DM．若△ODM的面积为3，则k的值为（ ）
A．2B．3C．4D．5
【答案】C
【解答】解：解法一：∵四边形OCBA是矩形，
∴AB＝OC，OA＝BC，设B点的坐标为（a，b），
∵矩形OABC的对称中心M，
∴延长OM恰好经过点B，M（，），
∵点D在AB上，且 AD＝AB，
∴D（，b），
∴BD＝a，
∴S△BDM＝BD•h＝×a×（b﹣）＝ab，
∵D在反比例函数的图象上，
∴ab＝k，
∵S△ODM＝S△AOB﹣S△AOD﹣S△BDM＝ab﹣k﹣ab＝3，
∴ab＝16，
∴k＝ab＝4，
解法二：连接BM，因为点M是矩形的对称中心，
∴三角形DMO的面积＝三角形DMB的面积，
则三角形DBO的面积为6，
∵AD＝1/4AB，
∴AD：DB＝1：3，
∴三角形ADO的面积：三角形DBO的面积为1：3，
即三角形ADO的面积为2，
∴K＝4．
故选：C．
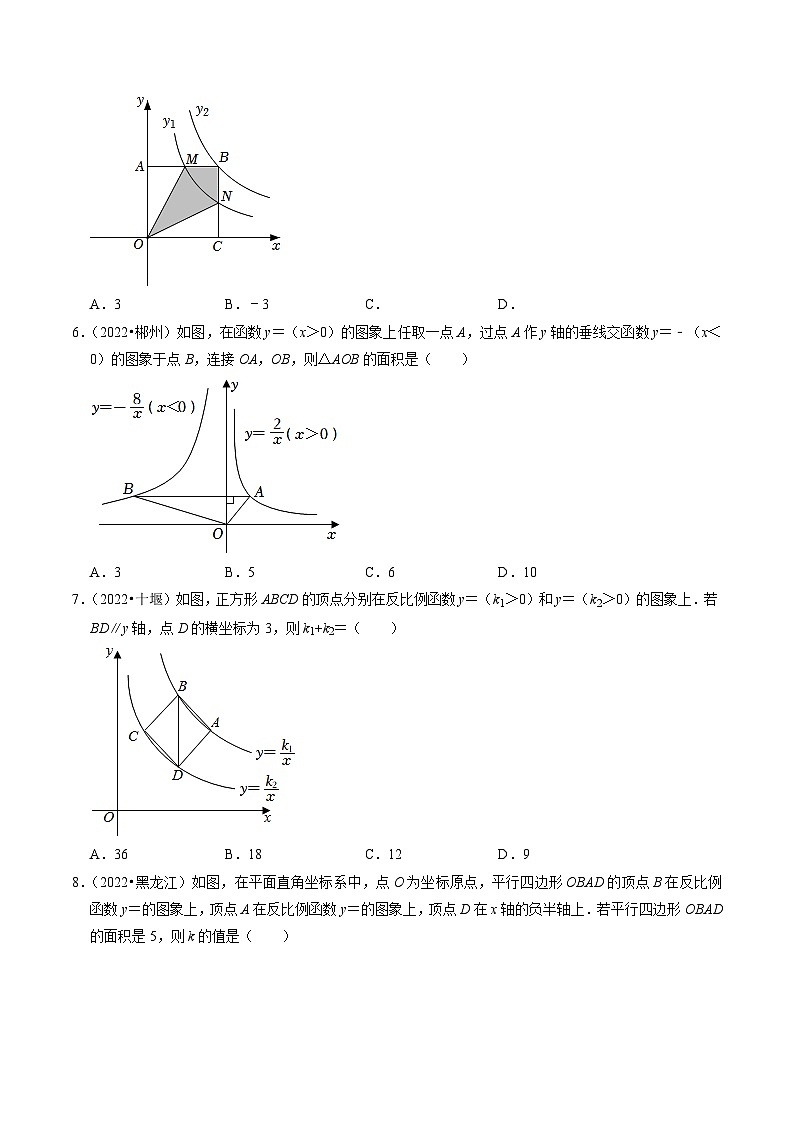
3．（2023•黑龙江）如图，△ABC是等腰三角形，AB过原点O，底边BC∥x轴，双曲线y＝过A，B两点，过点C作CD∥y轴交双曲线于点D．若S△BCD＝12，则k的值是（ ）
A．﹣6B．﹣12C．﹣D．﹣9
【答案】C
【解答】解：设BC与y轴的交点为F，B（b，），则A（﹣b，﹣），b＞0，由题意知，
AO＝BO，即O是线段AB的中点，过A作AE⊥BC于点E，
∵AC＝AB，AE⊥BC，
∴BE＝CE，AE∥y轴，
∴CF＝3BF＝3b，
∴C（﹣3b，），
∴D（﹣3b，），
∴CD＝，BC＝4b，
∴S△BCD＝，
∴k＝﹣．
故选：C．
4．（2023•宜宾）如图，在平面直角坐标系xOy中，点A、B分别在y、x轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（ ）
A．B．C．D．
【答案】B
【解答】解：如图，过点N作NQ⊥x轴于点Q，过C作CT⊥y轴交y轴于T，交NQ于K，
设OA＝a，OP＝b，BM＝c，N（m，n），
∵OP：BP＝1：4，BM＝CM，
∴A（0，a），B（5b，0），M（5b，c），C（5b，2c），
∵∠NCK＝∠ACT，∠NKC＝90°＝∠ATC，
∴△NKC∽△ATC，
∴＝＝，
∵NC＝2AN，
∴CK＝2TK，NK＝AT，
∴，
解得，
∴，
∴，，
∴，
∵△APN的面积为3，
∴S梯形OANQ﹣S△AOP﹣S△NPQ＝3，
∴，
∴2ab+bc＝9，
将点M（5b，c）， 代入得：
，
整理得：2a＝7c，
将2a＝7c代入2ab+bc＝9得：7bc+bc＝9，
∴，
∴，
故选：B．
5．（2022•日照）如图，矩形OABC与反比例函数y1＝（k1是非零常数，x＞0）的图象交于点M，N，与反比例函数y2＝（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1﹣k2＝（ ）
A．3B．﹣3C．D．
【答案】B
【解答】解：∵y1、y2的图象均在第一象限，
∴k1＞0，k2＞0，
∵点M、N均在反比例函数y1＝（k1是非零常数，x＞0）的图象上，
∴S△OAM＝S△OCN＝k1，
∵矩形OABC的顶点B在反比例函数y2＝（k2是非零常数，x＞0）的图象上，
∴S矩形OABC＝k2，
∴S四边形OMBN＝S矩形OABC﹣S△OAM﹣S△OCN＝3，
∴k2﹣k1＝3，
∴k1﹣k2＝﹣3，
故选：B．
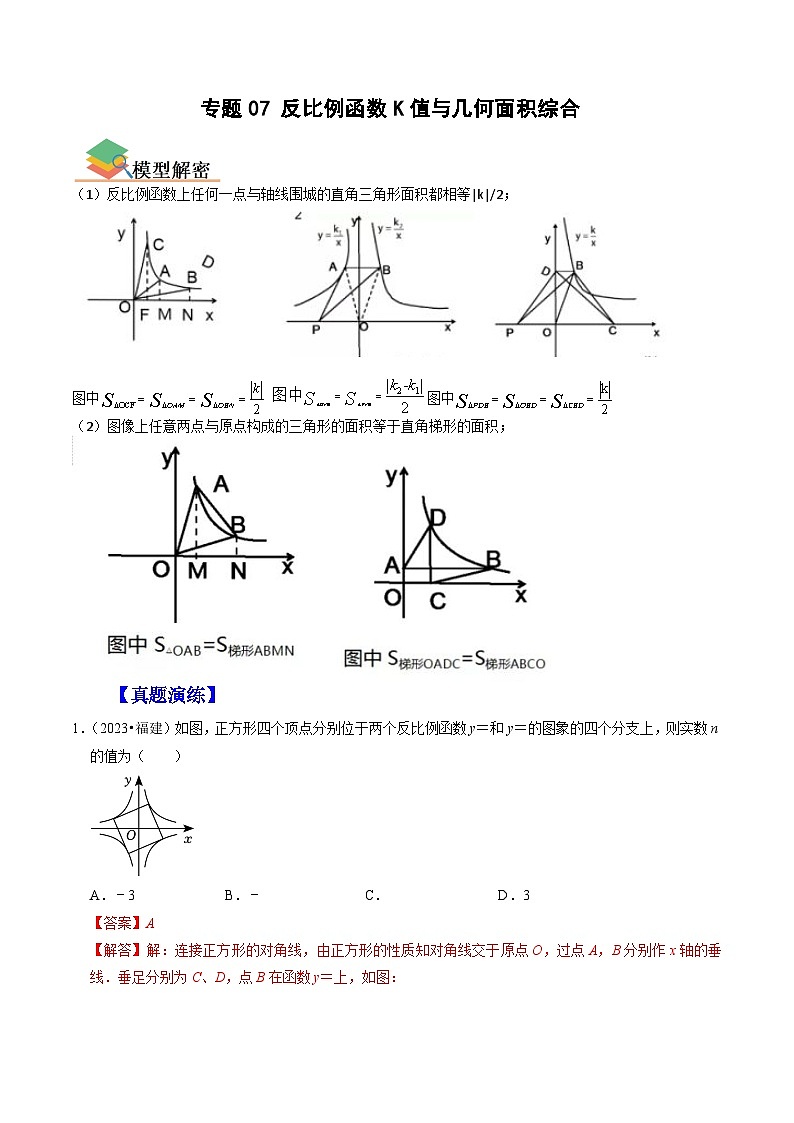
6．（2022•郴州）如图，在函数y＝（x＞0）的图象上任取一点A，过点A作y轴的垂线交函数y＝﹣（x＜0）的图象于点B，连接OA，OB，则△AOB的面积是（ ）
A．3B．5C．6D．10
【答案】B
【解答】解：∵点A在函数y＝（x＞0）的图象上，
∴S△AOC＝×2＝1，
又∵点B在反比例函数y＝﹣（x＜0）的图象上，
∴S△BOC＝×8＝4，
∴S△AOB＝S△AOC+S△BOC
＝1+4
＝5，
故选：B．
7．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（ ）
A．36B．18C．12D．9
【答案】B
【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：
∵四边形ABCD是正方形，
∴AE＝BE＝CE＝DE，
设AE＝BE＝CE＝DE＝m，D（3，a），
∵BD∥y轴，
∴B（3，a+2m），A（3+m，a+m），
∵A，B都在反比例函数y＝（k1＞0）的图象上，
∴k1＝3（a+2m）＝（3+m）（a+m），
∵m≠0，
∴m＝3﹣a，
∴B（3，6﹣a），
∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，
∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，
∴k1+k2＝18﹣3a+3a＝18；
故选：B．
8．（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（ ）
A．2B．1C．﹣1D．﹣2
【答案】D
【解答】解：设B（a，），
∵四边形OBAD是平行四边形，
∴AB∥DO，
∴A（，），
∴AB＝a﹣，
∵平行四边形OBAD的面积是5，
∴（a﹣）＝5，
解得k＝﹣2，
故选：D．
9．（2023•连云港）如图，矩形OABC的顶点A在反比例函数y＝（x＜0）的图象上，顶点B、C在第一象限，对角线AC∥x轴，交y轴于点D．若矩形OABC的面积是6，cs∠OAC＝，则k＝ ﹣ ．
【答案】﹣．
【解答】解：作AE⊥x轴于E，
∵矩形OABC的面积是6，
∴△AOC的面积是3，
∵∠AOC＝90°，cs∠OAC＝，
∴，
∵对角线AC∥x轴，
∴∠AOE＝∠OAC，
∵∠OEA＝∠AOC＝90°，
∴△OEA∽△AOC，
∴，
∴，
∴S△OEA＝，
∵S△OEA＝|k|，k＜0，
∴k＝﹣．
故答案为：﹣．
10．（2023•枣庄）如图，在反比例函数（x＞0）的图象上有P1，P2，P3，…P2024等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，…，S2023，则S1+S2+S3+…+S2023＝ ．
【答案】．
【解答】解：∵P1，P2，P3，…P2024的横坐标依次为1，2，3，…，2024，
∴阴影矩形的一边长都为1，
将除第一个矩形外的所有矩形向左平移至y轴，
∴S1+S2+S3+…+S2023＝，
把x＝2024代入关系式得，y＝，即OA＝，
∴S矩形OABC＝OA•OC＝，
由几何意义得，＝8，
∴＝8﹣＝．
故答案为：．
11．（2023•朝阳）如图，点A是反比例函数y＝（k≠0，x＞0）的图象上一点，过点A作AB⊥x轴于点B，点P是y轴上任意一点，连接PA，PB．若△ABP的面积等于3，则k的值为 6 ．
【答案】6．
【解答】解：设反比例函数的解析式为 y＝，
∵△AOB的面积＝△ABP的面积＝3，△AOB的面积＝|k|，
∴|k|＝3，
∴k＝±6；
又∵反比例函数的图象的一支位于第一象限，
∴k＞0．
∴k＝6．
故答案为：6．
12．（2023•衢州）如图，点A，B在x轴上，分别以OA，AB为边，在x轴上方作正方形OACD，ABEF，反比例函数y＝（k＞0）的图象分别交边CD，BE于点P，Q．作PM⊥x轴于点M，QN⊥y轴于点N．若OA＝2AB，Q为BE的中点，且阴影部分面积等于6，则k的值为 24 ．
【答案】见试题解答内容
【解答】解：设OA＝4a，
∵AO＝2AB，
∴AB＝2a，
∴OB＝AB+OA＝6a，则B（6a，0），
由于在正方形ABEF中，AB＝BE＝2a，
∵Q为BE中点，
∴BQ＝AB＝a，
∴Q（6a，a），
∵Q在反比例函数y＝（k＞0））上，
∴k＝6a×a＝6a2，
∵四边形OACD是正方形，
∴C（4a，4a），
∵P在CD上，
∴P点纵坐标为4a，
∵P在反比例函数y＝（k＞0）上，
∴P点横坐标为：x＝，
∴P（，4a），
∵作PM⊥x轴于点M，QN⊥y轴于点N，
∴四边形OMNH是矩形，
∴NH＝，MH＝a，
∴S矩形OMHN＝NH×MH＝×a＝6，
则k＝24，
故答案为：24．
13．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为 4 ．
【答案】4．
【解答】解：过点C作CD⊥y轴于点D，如图：
设点C的坐标为（a，b），点A的坐标为（0，c），
∴CD＝a，OA＝c，
∵△AOC的面积是6，
∴，
∴ac＝12，
∵点C（a，b）在反比例函数（x＞0）的图象上，
∴k＝ab，
∵点B为AC的中点，
∴点，
∵点B在反比例函数（x＞0）的图象上，
∴，
即：4k＝a（b+c），
∴4k＝ab+ac，
将ab＝k，ac＝12代入上式得：k＝4．
故答案为：4．
14．（2023•黄石）如图，点A（a，） 和B（b，）在反比例函数y＝（k＞0）的图象上，其中a＞b＞0．过点A作AC⊥x轴于点C，则△AOC的面积为 ；若△AOB的面积为，则＝ 2 ．
【答案】，2．
【解答】解：因为点A（a，）在反比例函数y＝的图象上，
则，又a＞0，
解得k＝5．
根据k的几何意义可知，
．
过点B作x轴的垂线，垂足为D，
则S△OBD+S梯形ACDB＝S△AOC+S△AOB，
又根据k的几何意义可知，
S△OBD＝S△AOC，
则S梯形ACDB＝S△AOB．
又△AOB的面积为，且A（a，），B（b，），
所以，
即．
解得．
又a＞b＞0，
所以．
故答案为：，2．
15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为 6 ．
【答案】6．
【解答】解：如图，延长CD交y轴于E，连接OD，
∵矩形ABCD的面积是8，
∴S△ADC＝4，
∵AC＝2AO，
∴S△ADO＝2，
∵AD∥OE，
∴△ACD∽△OCE，
∴AD：OE＝AC：OC＝2：3，
∴S△ODE＝3，
由几何意义得，＝3，
∵k＞0，
∴k＝6，
故答案为：6．
16．（2023•绍兴）如图，在平面直角坐标系xOy中，函数（k为大于0的常数，x＞0）图象上的两点A（x1，y1），B（x2，y2），满足x2＝2x1，△ABC的边AC∥x轴，边BC∥y轴，若△OAB的面积为6，则△ABC的面积是 2 ．
【答案】2．
【解答】解：如图，延长CA交y轴于E，延长CB交x轴于点F，
∴CE⊥y轴，CF⊥x轴，
∴四边形OECF为矩形，
∵x2＝2x1，
∴点A为CE的中点，
由几何意义得，S△OAE＝S△OBF，
∴点B为CF的中点，
∴S△OAB＝S矩形OECF＝6，
∴S矩形OECF＝16，
∴S△ABC＝×16＝2．
故答案为：2．
2
17．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为 6 ．
【答案】见试题解答内容
【解答】解：因为D为AC的中点，△AOD的面积为3，
所以△AOC的面积为6，
所以k＝12＝2m．
解得：m＝6．
故答案为：6．
18．（2022•黄石）如图，反比例函数y＝的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，△OCE的面积为6，则k＝ 8 ．
【答案】8．
【解答】解：如图，过点E作EH⊥BC于H，
设点A（a，），C（c，0），
∵点E是矩形ABCD的对角线的交点，
∴E（，），
∵点E在反比例函数y＝的图象上，
∴＝k，
∴c＝3a，
∵△OCE的面积为6，
∴OC•EH＝c•＝×3a•＝6，
∴k＝8，
故答案为：8．
19．（2022•衢州）如图，在△ABC中，边AB在x轴上，边AC交y轴于点E．反比例函数y＝（x＞0）的图象恰好经过点C，与边BC交于点D．若AE＝CE，CD＝2BD，S△ABC＝6，则k＝ ．
【答案】．
【解答】解：如图，作CM⊥AB于点M，DN⊥AB于点N，
设C（m，），
则OM＝m，CM＝，
∵OE∥CM，AE＝CE，
∴＝＝1，
∴AO＝m，
∵DN∥CM，CD＝2BD，
∴＝＝＝，
∴DN＝，
∴D的纵坐标为，
∴＝，
∴x＝3m，
即ON＝3m，
∴MN＝2m，
∴BN＝m，
∴AB＝5m，
∵S△ABC＝6，
∴5m•＝6，
∴k＝．
故答案为：．
20．（2022•宜宾）如图，△OMN是边长为10的等边三角形，反比例函数y＝（x＞0）的图象与边MN、OM分别交于点A、B（点B不与点M重合）．若AB⊥OM于点B，则k的值为 9 ．
【答案】9．
【解答】解：过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，如图，
∵△OMN是边长为10的等边三角形，
∴OM＝ON＝MN＝10，∠MON＝∠M＝∠MNO＝60°
设OC＝b，则BC＝，OB＝2b，
∴BM＝OM﹣OB＝10﹣2b，B（b，b），
∵∠M＝60°，AB⊥OM，
∴AM＝2BM＝20﹣4b，
∴AN＝MN﹣AM＝10﹣（20﹣4b）＝4b﹣10，
∵∠AND＝60°，
∴DN＝＝2b﹣5，AD＝AN＝2b﹣5，
∴OD＝ON﹣DN＝15﹣2b，
∴A（15﹣2b，2b﹣5），
∵A、B两点都在反比例函数y＝（x＞0）的图象上，
∴k＝（15﹣2b）（2b﹣5）＝b•b，
解得b＝3或5，
当b＝5时，OB＝2b＝10，此时B与M重合，不符题意，舍去，
∴b＝3，
∴k＝b•b＝9，
故答案为：9．
21．（2022•鄂尔多斯）如图，正方形OABC的顶点A、C分别在x轴和y轴上，E、F分别是边AB、OA上的点，且∠ECF＝45°，将△ECF沿着CF翻折，点E落在x轴上的点D处．已知反比例函数y1＝和y2＝分别经过点B、点E，若S△COD＝5，则k1﹣k2＝ 10 ．
【答案】见试题解答内容
【解答】解：作EH⊥y轴于点H，
则四边形BCHE、AEHO都为矩形，
∵∠ECF＝45°，
∴∠OCD+∠OCF＝45°，
∵∠DOC+∠OCF＝45°，
∴∠BCE＝∠OCD，
∵BC＝OC，∠B＝∠COD，
∴△BCE≌△OCD（ASA），
∴S△BCE＝S△COD＝5，
∴S△CEH＝5，
S矩形BCHE＝10，
∴根据反比例函数系数k的几何意义得：
k1﹣k2＝S矩形BCHE＝10，
故答案为：10．
22．（2022•东营）如图，△OAB是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数y＝（x＞0）的图象上，则经过点A的函数图象表达式为 y＝﹣ ．
【答案】y＝﹣．
【解答】解：如图，作AD⊥x轴于D，BC⊥x轴于C，
∴∠ADO＝∠BCO＝90°，
∵∠AOB＝90°，
∴∠AOD+∠BOC＝90°，
∴∠AOD+∠DAO＝90°，
∴∠BOC＝∠DAO，
∵OB＝OA，
∴△BOC≌△OAD（AAS），
∵点B在反比例函数y＝（x＞0）的图象上，
∴S△OBC＝，
∴S△OAD＝，
∴k＝﹣1，
∴经过点A的反比例函数解析式为y＝﹣．
故答案为：y＝﹣．
23．（2022•绍兴）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C和DE的中点F，则k的值是 6 ．
【答案】6．
【解答】解：过点F作FG⊥x轴于点G，FH⊥y轴于点H，过点D作DQ⊥x轴于点Q，如图所示，
根据题意可知，AC＝OE＝BD，
设AC＝OE＝BD＝a，
∴四边形ACEO的面积为4a，
∵F为DE的中点，FG⊥x轴，DQ⊥x轴，
∴FG为△EDQ的中位线，
∴FG＝DQ＝2，EG＝EQ＝，
∴四边形HFGO的面积为2（a+），
∴k＝4a＝2（a+），
解得：a＝，
∴k＝6．
故答案为：6．
24．（2022•内蒙古）如图，在平面直角坐标系中，Rt△OAB的直角顶点B在x轴的正半轴上，点O与原点重合，点A在第一象限，反比例函数y＝（x＞0）的图象经过OA的中点C，交AB于点D，连接CD．若△ACD的面积是1，则k的值是 ．
【答案】．
【解答】解：连接OD，过C作CE∥AB，交x轴于E，
∵∠ABO＝90°，反比例函数y＝（x＞0）的图象经过OA的中点C，
∴S△COE＝S△BOD＝k，S△ACD＝S△OCD＝1，
∵CE∥AB，
∴△OCE∽△OAB，
∴△OCE与△OAB得到面积比为1：4，
∴4S△OCE＝S△OAB，
∴4×k＝1+1+k，
∴k＝．
故答案为：．