










数学3.4 函数的应用优秀练习题习题ppt课件
展开3.4 函数的应用
许多实际问题都可以通过建立函数模型来解决,函数模型是应用最广泛的数学模型之一.实际问题一旦被认定为函数关系,就可以通过研究这个函数的性质,使问题得以解决.
我国是世界上高速铁路系统技术最全、集成能力最强、运营里程最长、运行速度最高、在建规模最大的国家.近年来,我国高铁飞速发展.条条高铁悄然改变着人们的生活,已成为人们出行的快捷方式之一.开通某条高铁线路前,需要进行安全、平稳测试.
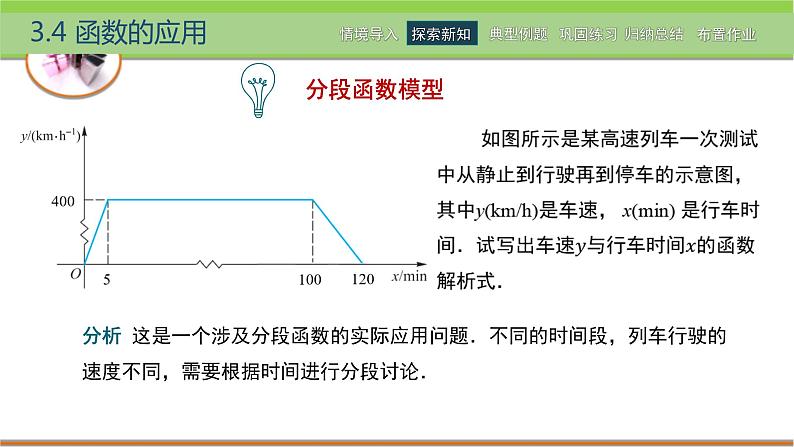
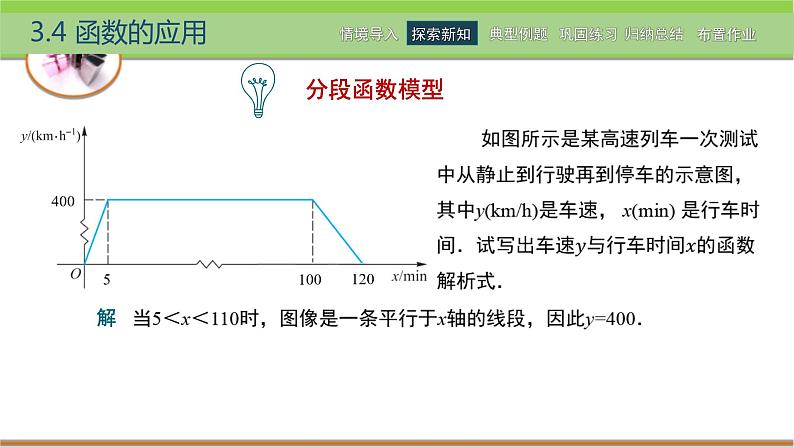
分析 这是一个涉及分段函数的实际应用问题.不同的时间段,列车行驶的速度不同,需要根据时间进行分段讨论.
分析 这是一个有关二次函数的实际应用问题.通过矩形面积公式可得所求函数关系式.利用二次函数模型可求得窗框所围成的最大面积.
如今,智慧农业深入民心,通过科学种植可以大幅提高农产品的产量.实践证明,果树栽培过程中栽种密度过大,果树之间的透气性就会受到影响,不能保证有足够的光照度,水果的产量和品质都会受到影响.
通过数据分析,在某果园内种植面积不变的情况下,如果按照种植50棵果树计算,平均每棵树可以产果600个.如果种植密度增加,每多种一棵树,平均每棵树就会减少结果5个. (1)果园增种多少棵果树时候,水果总产量最大?最大产量是多少? (2)如果要使水果总产量不少于33000个,应该如何安排种植数目?
分析 这也是一个关于二次函数的实际应用题,利用水果总产量=果树总数×单棵平均产量得到函数解析式,转化为二次函数,再利用二次函数的性质解决问题.
(2)由使水果的总产量y不少于33000个,则-5x²+350x+30000≥33000,整理得 -5x²+350x-3000≥0,即x²-70x+600≤0 . 解不等式得10≤x≤60. 因此要使水果总产量不少于33000个,该果园内至少要增种10棵果树,但不能超过60棵.
已知定义在D上的函数f(x). (1)如果对任意x∈D,都有f(x)≤ M ,且存在x0∈D,使f(x0)= M ,则称M是函数f(x)的最大值; (2)如果对任意x∈D,都有f(x) ≥m,且存在x0∈D,使f(x0)=m,则称m是函数f(x)的最小值. 函数的最大值或最小值统称函数的最值. 当应用函数模型求解问题时,应根据实际情况考虑函数 的定义域,特别是求函数的最大(小)值时,要考虑自变量是否有取整的需要.
试画出一次函数模型“情境与问题”和二次函数模型“情境与问题(1)”中的函数图像.这两个图像有什么特点?
2.某市出租车车费标准如下:3km以内(含3km )收费8元;超过3km的部分每千米收费1.6元. (1)写出应收费y(元)与出租车行驶路程x(km)之间的关系式. (2)小亮乘车行驶4km ,应付多少元? (3)小波下车时付车费16元,那么小波乘出租车行驶了多远?
3.某商品现在的售价为60元/件,每星期可卖出300件.市场调查反映,该商品的合理售价应不低于30元/件,不高于70元/件.若调整商品售价,每降价(提价)1元/件,每星期可多(少)卖出20件.设商品售价降价(提价)x(元/件)后,每星期售出商品的总销售额为y(元).求y与x之间的函数解析式.
数学基础模块 上册1.2 集合之间的关系优秀练习题习题ppt课件: 这是一份数学基础模块 上册<a href="/sx/tb_c4036573_t3/?tag_id=26" target="_blank">1.2 集合之间的关系优秀练习题习题ppt课件</a>,文件包含12集合之间的关系课件pptx、12集合之间的关系教案docx、12集合之间的关系课内习题答案docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
高教版(2021·十四五)基础模块 上册1.1 集合及其表示优秀练习题习题ppt课件: 这是一份高教版(2021·十四五)基础模块 上册<a href="/sx/tb_c4036572_t3/?tag_id=26" target="_blank">1.1 集合及其表示优秀练习题习题ppt课件</a>,文件包含11集合及其表示课件pptx、11集合及其表示教案docx、11集合及其表示课内习题答案docx等3份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
高教版(2021·十四五)基础模块 上册1.1 集合及其表示优质课练习题习题课件ppt: 这是一份高教版(2021·十四五)基础模块 上册<a href="/sx/tb_c4036572_t3/?tag_id=26" target="_blank">1.1 集合及其表示优质课练习题习题课件ppt</a>,文件包含11集合及其表示课件pptx、11集合及其表示教案docx、11集合及其表示课内习题答案docx等3份课件配套教学资源,其中PPT共32页, 欢迎下载使用。












