2024年上海市青浦区高三下学期4月学业质量调研数学试卷含答案

这是一份2024年上海市青浦区高三下学期4月学业质量调研数学试卷含答案，共13页。试卷主要包含了04， ；14等内容，欢迎下载使用。

（时间120分钟，满分150分） 2024.04
学生注意：
本试卷包括试卷纸和答题纸两部分．
在试卷纸上答题无效，必须在答题纸上的规定位置按照要求答题．
可使用符合规定的计算器答题．
填空题（本大题共有12题，满分54分，第1-6每题4分，第7-12每题5分）考生应在答题纸的相应位置直接填写结果.
1．不等式的解集为____________．
2．已知向量，，则____________．
3．已知复数，则____________．
4．的二项展开式中的常数项为____________．
5．设随机变量服从正态分布，若，则实数_____．
6．椭圆的离心率为，则____________．
7．已知直线的倾斜角比直线的倾斜角小，则的斜率为____________．
8．已知，，若，则满足条件的 的取值范围是____________．
9．对于函数，其中，若关于的方程有两个不同的零点，则实数的取值范围是____________．
10．从中任取个不同的数字，设“取到的个数字之和为偶数”为事件，“取到的个数字均为奇数”为事件，则_________．
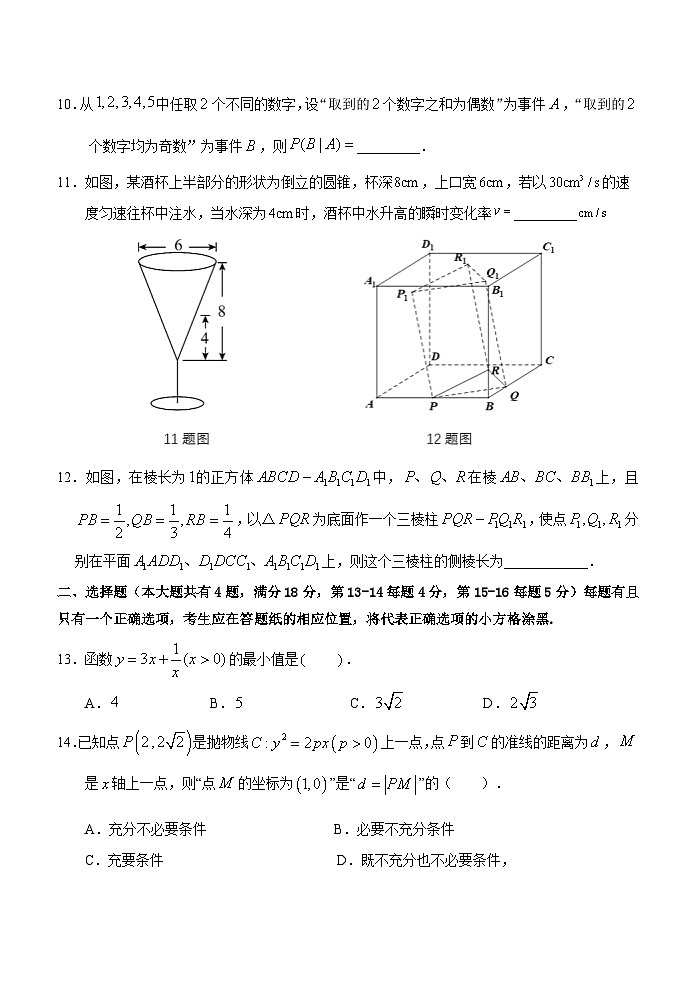
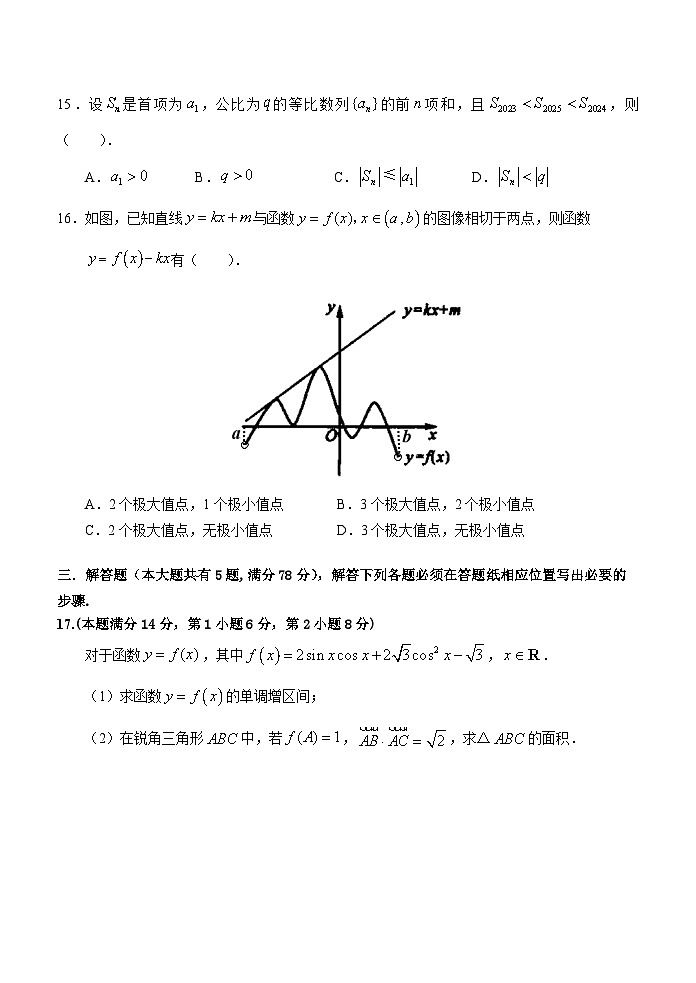
11．如图，某酒杯上半部分的形状为倒立的圆锥，杯深，上口宽，若以的速度匀速往杯中注水，当水深为时，酒杯中水升高的瞬时变化率_________
12．如图，在棱长为的正方体中，在棱上，且，以△为底面作一个三棱柱，使点分别在平面上，则这个三棱柱的侧棱长为____________．
二、选择题（本大题共有4题，满分18分，第13-14每题4分，第15-16每题5分）每题有且只有一个正确选项，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.
13．函数的最小值是 ．
A．B．C．D．
14．已知点是抛物线上一点，点到的准线的距离为，是轴上一点，则“点的坐标为”是“”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件，
15．设是首项为，公比为的等比数列的前项和，且，则（ ）．
A．B．C．D．
16．如图，已知直线与函数的图像相切于两点，则函数有（ ）．
A．2个极大值点，1个极小值点B．3个极大值点，2个极小值点
C．2个极大值点，无极小值点D．3个极大值点，无极小值点
三．解答题（本大题共有5题,满分78分），解答下列各题必须在答题纸相应位置写出必要的步骤.
17.(本题满分14分，第1小题6分，第2小题8分)
对于函数，其中，．
（1）求函数的单调增区间；
（2）在锐角三角形中，若，，求△的面积．
18．（本题满分14分，第1小题6分，第2小题8分）
如图，三棱柱是所有棱长均为的直三棱柱，分别是棱和棱的中点．
（1）求证：平面平面；
（2）求二面角的余弦值大小．
19.(本题满分14分，第1小题4分，第2小题（ = 1 \* rman i）4分，第2小题（ = 2 \* rman ii）6分)
垃圾分类能减少有害垃圾对环境的破坏，同时能提高资源循环利用的效率．目前上海社区的垃圾分类基本采用四类分类法，即干垃圾，湿垃圾，可回收垃圾与有害垃圾．某校为调查学生对垃圾分类的了解程度，随机抽取100名学生作为样本，按照了解程度分为A等级和B等级，得到如下列联表：
（1）根据表中的数据回答：学生对垃圾分类的了解程度是否与性别有关（规定：显著性水平）？
附：，其中，．
（2）为进一步加强垃圾分类的宣传力度，学校特举办垃圾分类知识问答比赛．每局比赛由二人参加，主持人A和B轮流提问，先赢局者获得奖项并结束比赛．甲，乙两人参加比赛，已知主持人A提问甲赢的概率为，主持人B提问甲赢的概率为，每局比赛互相独立，且每局都分输赢．现抽签决定第一局由主持人A提问．
（ = 1 \* rman i）求比赛只进行3局就结束的概率；
（ = 2 \* rman ii）设为结束比赛时甲赢的局数，求的分布和数学期望．
20.(本题满分18分，第1小题4分，第2小题6分，第3小题8分)
已知双曲线，，分别为其左、右焦点．
（1）求，的坐标和双曲线的渐近线方程；
（2）如图，是双曲线右支在第一象限内一点，圆是△的内切圆，设圆与，，分别切于点，，，当圆的面积为时，求直线的斜率；
（3）是否存在过点的直线与双曲线的左右两支分别交于，两点，且使得，若存在，求出直线的方程；若不存在，请说明理由．
21（2）图

21.(本题满分18分，第1小题4分，第2小题6分，第3小题8分)
若无穷数列满足：存在正整数，使得对一切正整数成立，则称是周期为的周期数列．
（1）若（其中正整数m为常数，），判断数列是否为周期数列，并说明理由；
（2）若，判断数列是否为周期数列，并说明理由；
（3）设是无穷数列，已知．求证：“存在，使得是周期数列”的充要条件是“是周期数列”．
参考答案 2024.04
一.填空题（本大题满分54分）本大题共有12题，1-6每题4分，7-12每题5分考生应在答题纸相应编号的空格内直接填写结果.
1．；2．；
3．；4．；
5．；6．；
7．；8．；
9. ；10. ；
11．；12. .
二.选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.
13. ；14. ； 15． ；16..
三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
17.(本题满分14分）本题共2小题，第（1）小题6分，第（2）小题8分.
解：（1）

由，得
所以，函数的单调增区间是．
（2）由已知，所以
因为，所以，即，所以
又，所以，，
所以，△的面积．
18．（本题满分14分）第（1）小题满分6分，第（2）小题满分8分.
解：（1）为棱中点，△为正三角形，.
又三棱柱是直三棱柱，
平面，又平面，，
因为
平面平面，
平面，平面平面
（2）由（1）得平面， 平面，
，是二面角的平面角
在△中，
二面角的余弦值为．
19.(本题满分14分，第1小题4分，第2小题（ = 1 \* rman i）4分，第2小题（ = 2 \* rman ii）6分)
解：（1）提出原假设:学生对垃圾分类的了解程度与性别无关，
确定显著性水平，由题意得，
可得，
由，且，
所以接受原假设，学生对垃圾分类的了解程度与性别无关.
（2）（i）比赛只进行3局就结束，甲赢得比赛的概率为
比赛只进行3局就结束，乙赢得比赛的概率为，
故比赛只进行3局就结束的概率为；
（ii）的可能取值为，
，即进行了3场比赛，且乙赢得比赛，故，
，即进行了4场比赛，且乙赢得比赛，前3场中，甲赢得1场比赛，乙第4场赢，
故，
，即进行了5场比赛，且乙赢得比赛，前4场中，甲赢得2场比赛，乙第5场赢，
故
，
，即最后甲赢得比赛，由概率性质得，
所以分布为
故数学期望为
20.(本题满分18分）本题共3小题，第（1）小题4分，第（2）小题6分，第（3）小题8分.
解：（1）因为双曲线，所以，所以，
即，，
所以双曲线的渐近线方程是
（2）解法一：由题意可知，，，
所以，
，即是椭圆右顶点
设圆的半径为，因为圆的面积为，则，即，
，
设直线的斜率为，则直线的方程为，即，
由圆心到直线的距离等于圆的半径，
可得，
解得直线的斜率为
（3）假设存在过点的直线与双曲线的左右两支分别交于，两点，且使得，
设，，，，中点为，，
又，，
由，可知△为等腰三角形，，且直线不与轴重合，
于是，即，
因此，，
，点，在双曲线上，
所以，
①②化简整理得：，，
则，
可得，
，
联立（Ⅰ）（Ⅱ）得，，
得或（舍）所以
由，得，
所以直线的方程为．
21.(本题满分18分）本题共3小题，第（1）小题4分，第（2）小题6分，第（3）小题8分.
解：（1）∵
∴是为周期为的周期数列．
（2）①当时，，，
∴当时，是周期为1的周期数列；
②当时，记，则，
，当且仅当时等号成立．
即，所以在上严格增．
若，则，即，进而可得，即是严格增数列，不是周期数列；
同理，若，可得是严格减数列，不是周期数列．
综上，当时，是周期为1的周期数列；当时，不是周期数列．
（3）证明：
必要性．
若存在，使得是周期数列，设的周期为，则
，
所以是周期为的周期数列．
充分性．
若是周期数列，设它的周期为，记，则
，是关于x的连续函数；
，是关于x的连续函数；
…
，是关于x的连续函数；
，
令，则是连续函数，且
，，
∴存在零点．于是
取，则，从而
，
，
……
一般地，对任何正整数n都成立，即是周期为T的周期数列．
（说明：关于函数连续性的说明不作要求）
男生
女生
总计
A等级
40
20
60
B等级
20
20
40
总计
60
40
100
0
1
2
3