高考数学考前回顾复习《三角函数与解三角形》课件

这是一份高考数学考前回顾复习《三角函数与解三角形》课件，共55页。PPT课件主要包含了必考知识，常用结论，经典重温，k∈Z，x＝kπk∈Z，横坐标，纵坐标，－sinα，cosα，－cosα等内容，欢迎下载使用。
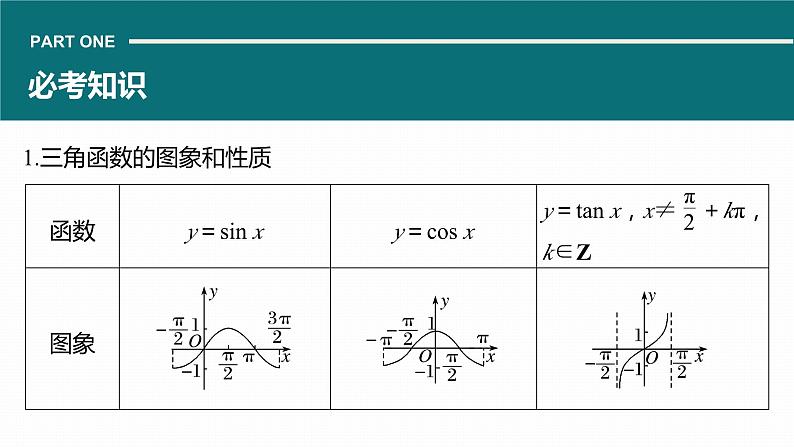
1.三角函数的图象和性质
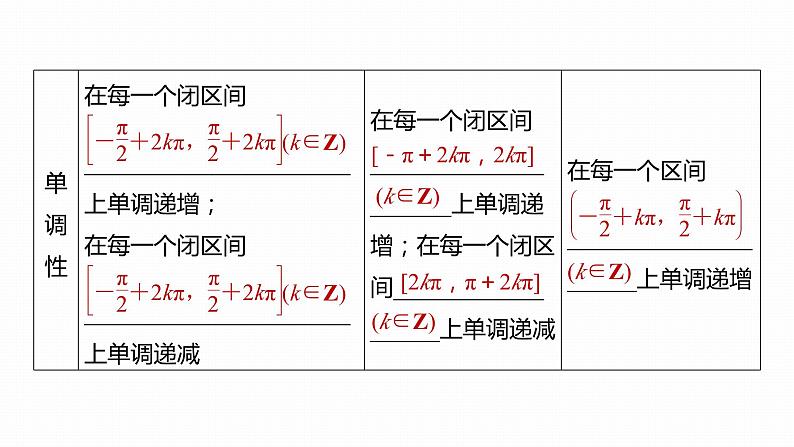
[－π＋2kπ，2kπ]
[2kπ，π＋2kπ]
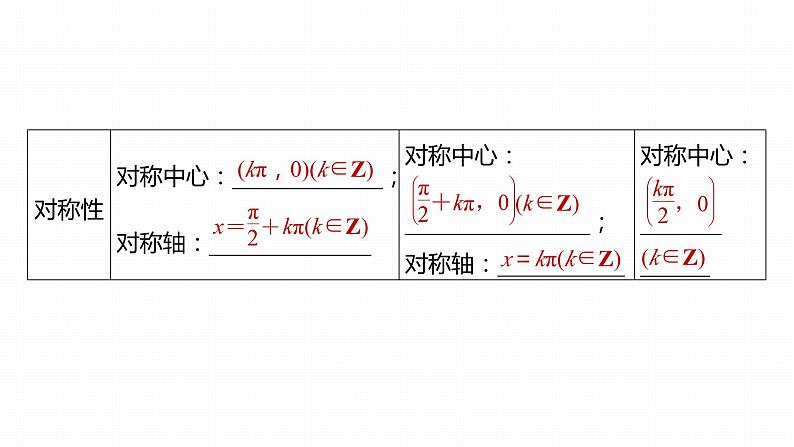
(kπ，0)(k∈Z)
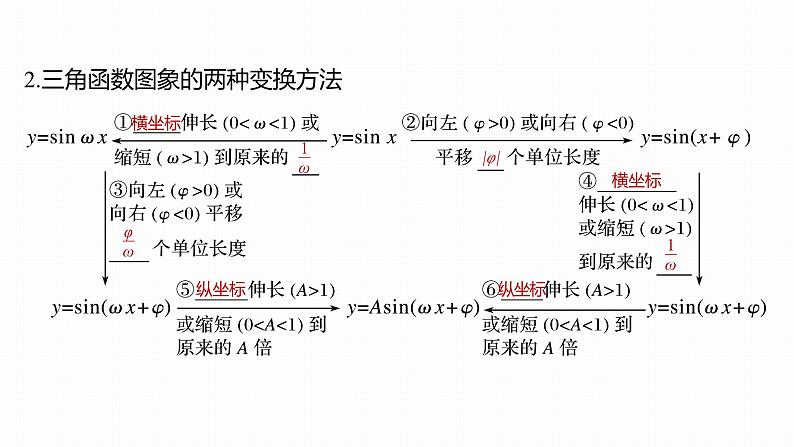
2.三角函数图象的两种变换方法
3.同角三角函数的基本关系式及诱导公式(1)平方关系：sin2α＋cs2α＝ .(2)商数关系：
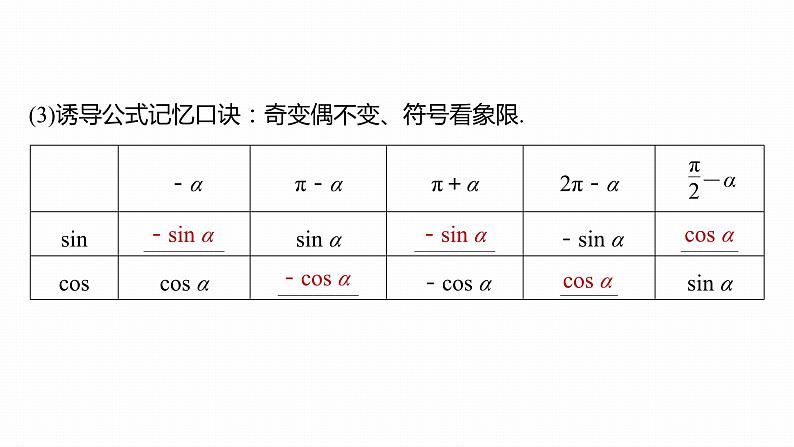
(3)诱导公式记忆口诀：奇变偶不变、符号看象限.
4.两角和与差的正弦、余弦、正切公式及倍角公式sin(α±β)＝ sin 2α＝ .cs(α±β)＝ cs 2α＝ ＝ ＝ .tan(α±β)＝ tan 2α＝ .cs2α＝ ，sin2α＝ .
sin αcs β±cs αsin β
cs αcs β∓sin αsin β
6.正弦定理及其变形在△ABC中， ＝ ＝ ＝2R(R为△ABC的外接圆半径).
7.余弦定理及其变形在△ABC中，a2＝ ；b2＝a2＋c2－2accs B；c2＝a2＋b2－2abcs C.变形：b2＋c2－a2＝ ；a2＋c2－b2＝2accs B；a2＋b2－c2＝2abcs C.
b2＋c2－2bccs A
cs A＝ ；cs B＝ ；cs C＝ .
1.三角恒等变换的常用技巧
②特殊三角函数值的代换.
2.三角函数图象平移问题处理策略(1)看平移要求：首先要看题目要求由哪个函数平移得到哪个函数，这是判断移动方向的关键点.(2)看移动方向：移动的方向一般记为“正向左，负向右”，看y＝Asin(ωx＋φ)中φ的正负和它的平移要求.(3)看移动的单位长度：在函数y＝Asin(ωx＋φ)中，周期变换和相位变换都是沿x轴方向的，所以ω和φ之间有一定的关系，φ是初相，再经过ω的压缩，最后移动的单位长度是 .
3.三角形中的常见结论(1)有关角的结论
1.(2023·潍坊模拟)若角α的终边过点P(3，－4)，则sin 2α的值为
∵角α的终边过点P(3，－4)，∴|OP|＝5，
2.下列函数中，定义域为R且最小正周期为π的偶函数是A.f(x)＝sin xcs xB.f(x)＝tan xC.f(x)＝cs2x－sin2xD.f(x)＝|sin 2x|
对A，C，D三个选项观察得函数定义域都为R，即定义域关于原点对称；
∴排除B；对于A选项，∵f(－x)＝sin(－x)cs(－x)＝－sin xcs x＝－f(x)，∴f(x)是奇函数，∴排除A；
对于C选项，f(x)＝cs2x－sin2x＝cs 2x，
又∵f(－x)＝cs2(－x)－sin2(－x)＝cs2x－sin2x＝f(x)，∴f(x)是偶函数，∴C正确；
则T＝π，故ω＝2，则f(x)＝2sin(2x＋φ)，
先将函数y＝f(x)的图象上所有点的横坐标伸长为原来的3倍，
故函数g(x)在该区间上单调递减，故D正确.
∴ab＝a2＋b2－c2，
可得a＝2sin A，b＝2sin B，∴a＋b＝2sin A＋2sin B
7.(2023·开封模拟)在锐角△ABC中，a，b，c分别为角A，B，C所对的边.若2asin B＝ ，b＋c＝5，bc＝6，则a＝_____.
因为△ABC为锐角三角形，
解得－2＋12k≤ω≤2＋6k，k∈Z，且ω>0.
因为ω>0，所以当k