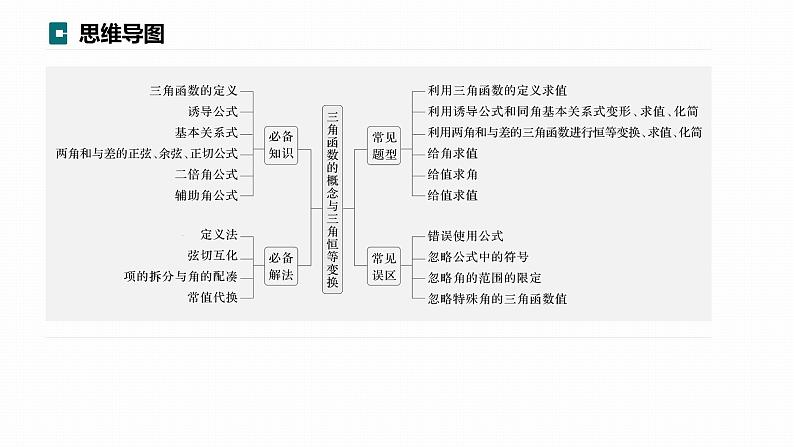
高考数学专题二　微专题14　三角函数的概念与三角恒等变换课件PPT

这是一份高考数学专题二　微专题14　三角函数的概念与三角恒等变换课件PPT，共56页。PPT课件主要包含了典例1，跟踪训练1，跟踪训练2，考点三三角恒等变换，典例3，跟踪训练3，∵θ∈0π等内容，欢迎下载使用。
三角函数的概念与三角恒等变换是高考常考内容，主要考查三角函数的概念、同角三角函数关系式、诱导公式，以及三角恒等变换的综合应用，给值求值问题.试题难度中等，常以选择题、填空题的形式出现.
考点一　三角函数的定义、诱导公式及基本关系式
则sin θ>0，cs θ>0，
则cs θ＝2sin θ，且cs2θ＋sin2θ＝4sin2θ＋sin2θ＝5sin2θ＝1，
典例2　(1)(2022·新高考全国Ⅱ)若sin(α＋β)＋cs(α＋β)＝ ，则A.tan(α－β)＝1B.tan(α＋β)＝1C.tan(α－β)＝－1D.tan(α＋β)＝－1
考点二　两角和与差的三角函数
则sin(2α＋β)－2sin αcs(α＋β)＝cs α，又sin(2α＋β)＝sin αcs(α＋β)＋cs αsin(α＋β)，所以cs αsin(α＋β)－sin αcs(α＋β)＝cs α，即sin β＝cs α，
方法一　因为tan θ＝－2，所以角θ的终边在第二或第四象限，
＝sin θ(sin θ＋cs θ)
方法二　(弦化切法)因为tan θ＝－2，
方法三　(正弦化余弦法)因为tan θ＝－2，所以sin θ＝－2cs θ.
因为5sin 2α＋5cs 2α＋1＝0，所以10sin αcs α＋5(cs2α－sin2α)＋cs2α＋sin2α＝0，整理得2sin2α－5sin αcs α－3cs2α＝0，则2tan2α－5tan α－3＝0，
整理可得tan β＋tan α＝tan αtan β－1，
＝sin 30°sin(θ＋15°)－cs 30°cs(θ＋15°)＋cs(θ＋45°)＝－cs(θ＋45°)＋cs(θ＋45°)＝0.