



所属成套资源:冲刺985、211名校高考数学重难点培优全攻略(新高考专用)
- 微重点06子数列与增减项问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用) 试卷 0 次下载
- 微重点07 球的切接问题(2大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用) 试卷 0 次下载
- 微重点09 截面、交线问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用) 试卷 0 次下载
- 微重点10 离心率的范围问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用) 试卷 0 次下载
- 微重点11圆锥曲线中二级结论的应用(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用) 试卷 0 次下载
微重点08 立体几何中的动态问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用)
展开这是一份微重点08 立体几何中的动态问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用),文件包含微重点08立体几何中的动态问题3大考点+强化训练原卷版docx、微重点08立体几何中的动态问题3大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
知识导图
考点分类讲解
考点一:动点轨迹问题
规律方法 解决与几何体有关的动点轨迹问题的方法
(1)几何法:根据平面的性质进行判定.
(2)定义法:转化为平面轨迹问题,用圆锥曲线的定义判定或用代数法进行计算.
(3)特殊值法:根据空间图形线段长度关系取特殊值或位置进行排除.
【例1】(2024·浙江温州·一模)如图,所有棱长都为1的正三棱柱,,点是侧棱上的动点,且,为线段上的动点,直线平面,则点的轨迹为( )
A.三角形(含内部)B.矩形(含内部)
C.圆柱面的一部分D.球面的一部分
【变式1】(多选)(23-24高三上·贵州安顺·期末)如图,在棱长为2的正方体中,点E、F、G、H分别为棱、、、的中点,点M为棱上动点,则( )
A.点E、F、G、H共面B.的最小值为
C.点B到平面的距离为D.
【变式2】(2023·贵州·一模)如图,已知正方体的棱长为2,M,N,P分别为棱的中点,Q为该正方体表面上的点,若M,N,P,Q四点共面,则点Q的轨迹围成图形的面积为 .
【变式3】(2023·宁波联考)正方体ABCD-A1B1C1D1的棱长为1,点P满足eq \(BP,\s\up6(→))=λeq \(BC,\s\up6(→))+μeq \(BB1,\s\up6(—→))(λ,μ∈R),则下列说法正确的有( )
A.若λ+μ=1,则A1P⊥AD1
B.若λ+μ=1,则三棱锥A1-PDC1的体积为定值
C.若点P总满足PA⊥BD1,则动点P的轨迹是一条直线
D.若点P到点A的距离为eq \r(3),则动点P的轨迹是一个面积为π的圆
考点二:折叠、展开问题
规律方法 画好折叠、展开前后的平面图形与立体图形,抓住两个关键点:不变的线线关系、不变的数量关系.
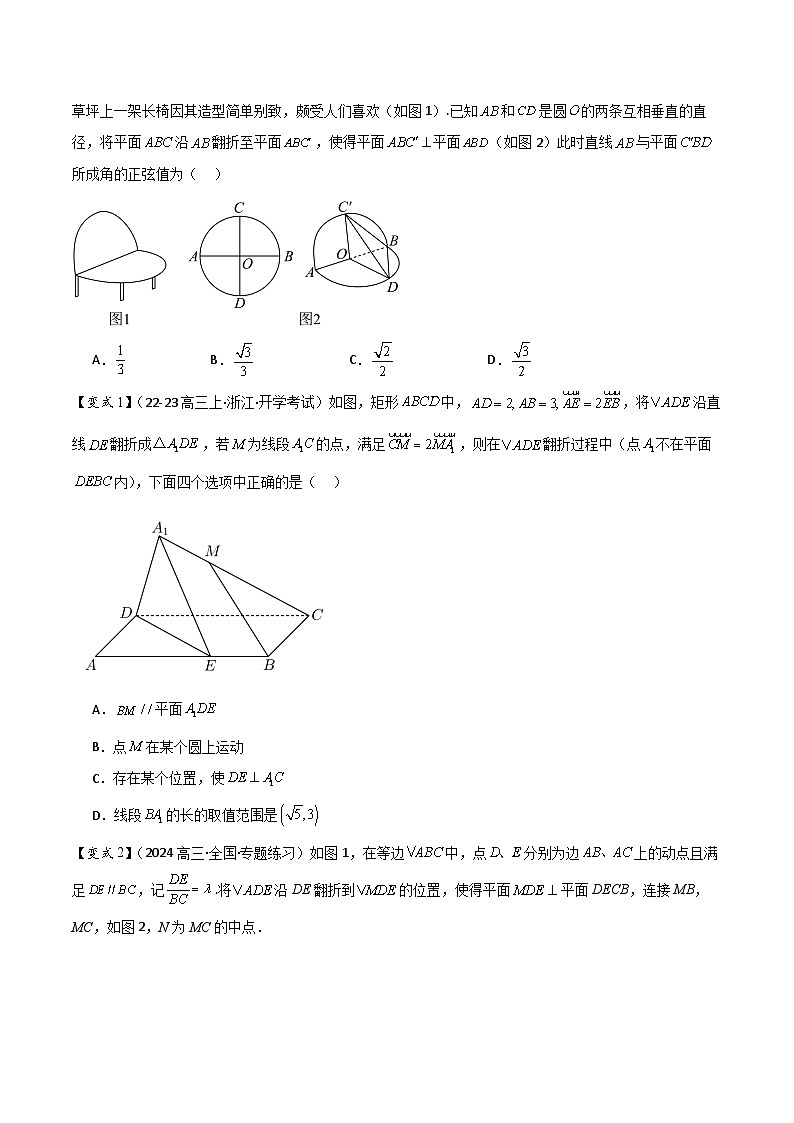
【例2】(2024·河南·模拟预测)为体现市民参与城市建设、共建共享公园城市的热情,同时搭建城市共建共享平台,彰显城市的发展温度,某市在中心公园开放长椅赠送点位,接受市民赠送的休闲长椅.其中观景草坪上一架长椅因其造型简单别致,颇受人们喜欢(如图1).已知和是圆的两条互相垂直的直径,将平面沿翻折至平面,使得平面平面(如图2)此时直线与平面所成角的正弦值为( )
A.B.C.D.
【变式1】(22-23高三上·浙江·开学考试)如图,矩形中,,将沿直线翻折成,若为线段的点,满足,则在翻折过程中(点不在平面内),下面四个选项中正确的是( )
A.平面
B.点在某个圆上运动
C.存在某个位置,使
D.线段的长的取值范围是
【变式2】(2024高三·全国·专题练习)如图1,在等边中,点分别为边上的动点且满足,记.将沿DE翻折到的位置,使得平面平面DECB,连接MB,MC,如图2,N为MC的中点.
(1)当平面MBD时,求的值.
(2)随着的值的变化,二面角的大小是否改变?若是,请说明理由;若不是,请求出二面角的正弦值.
【变式3】(2023·邵阳模拟)如图所示,在矩形ABCD中,AB=eq \r(3),AD=1,AF⊥平面ABCD,且AF=3,点E为线段CD(除端点外)上的动点,沿直线AE将△DAE翻折到△D′AE,则下列说法中正确的是( )
A.当点E固定在线段CD的某位置时,点D′的运动轨迹为球面
B.存在点E,使AB⊥平面D′AE
C.点A到平面BCF的距离为eq \f(\r(3),2)
D.异面直线EF与BC所成角的余弦值的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(13),13),\f(\r(10),10)))
考点三:最值、范围问题
规律方法 在动态变化过程中产生的体积最大、距离最大(小)、角的范围等问题,常用的解题思路是
(1)直观判断:在变化过程中判断点、线、面在何位置时,所求的量有相应最大、最小值.
(2)函数思想:通过建系或引入变量,把这类动态问题转化为目标函数,从而利用代数方法求目标函数的最值.
【例3】(多选)(2023·鞍山模拟)如图,正方体ABCD-A1B1C1D1的棱长为1,P是线段BC1上的动点,则下列结论正确的是( )
A.四面体PA1D1A的体积为定值
B.AP+PC的最小值为2eq \r(2)
C.A1P∥平面ACD1
D.直线A1P与AC所成的角的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,3)))
【变式1】(2023·青岛模拟)三面角是立体几何的基本概念之一,而三面角余弦定理是解决三面角问题的重要依据.三面角P-ABC是由有公共端点P且不共面的三条射线PA,PB,PC以及相邻两射线间的平面部分所组成的图形,设∠APC=α,∠BPC=β,∠APB=γ,二面角A-PC-B为θ,由三面角余弦定理得cs θ=eq \f(cs γ-cs α·cs β,sin α·sin β).在三棱锥P-ABC中,PA=6,∠APC=60°,∠BPC=45°,∠APB=90°,PB+PC=6,则三棱锥P-ABC体积的最大值为( )
A.eq \f(27\r(2),4) B.eq \f(27,4) C.eq \f(9,2) D.eq \f(9,4)
【变式2】(23-24高三下·北京·开学考试)正方体的棱长为1,动点在线段上,动点在平面上,且平面.线段长度的取值范围是( )
A.B.C.D.
【变式3】(2023·黑龙江哈尔滨·三模)已知四棱锥的底面为正方形,底面,点是线段上的动点,则直线与平面所成角的最大值为( )
A.B.C.D.
强化训练
一、单选题
1.(2023·云南保山·二模)已知正方体,Q为上底面所在平面内的动点,当直线与的所成角为45°时,点Q的轨迹为( )
A.圆B.直线C.抛物线D.椭圆
2.(2023·全国·三模)在平面直角坐标系中,为圆上的动点,定点.现将轴左侧半圆所在坐标平面沿轴翻折,与轴右侧半圆所在平面成的二面角,使点翻折至,仍在右侧半圆和折起的左侧半圆上运动,则,两点间距离的取值范围是( )
A.B.C.D.
3.(2024·全国·模拟预测)如图,已知矩形ABCD中,E为线段CD上一动点(不含端点),记,现将沿直线AE翻折到的位置,记直线CP与直线AE所成的角为,则( )
A.B.C.D.
4.(2023·上海宝山·二模)在空间直角坐标系中,已知定点,和动点.若的面积为,以为顶点的锥体的体积为,则的最大值为( )
A.B.C.D.
5.(23-24高三上·河北衡水·阶段练习)正三棱柱中,为的中点,为棱上的动点,为棱上的动点,且,则线段长度的取值范围为( )
A.B.
C.D.
6.(23-24高三下·山西·阶段练习)在棱长为4的正方体中,是的中点,是上的动点,则三棱锥外接球半径的最小值为( )
A.3B.C.D.
7.(2023·陕西咸阳·模拟预测)如图,点是棱长为2的正方体的表面上一个动点,则以下不正确的是( )
A.当在平面上运动时,四棱锥的体积不变
B.当在线段上运动时,与所成角的取值范围是
C.使直线与平面所成的角为的点的轨迹长度为
D.若是的中点,当在底面上运动,且满足平面时,长度的最小值是
8.(2023·吉林长春·模拟预测)四棱柱中,侧棱底面,,,,侧面为正方形,设点O为四棱锥外接球的球心,E为上的动点,则直线与所成的最小角的正弦值为( )
A.B.C.D.
二、多选题
1.(23-24高三下·江苏苏州·开学考试)在正方体中, 点为棱上的动点, 则( )
A.平面平面
B.平面平面
C.与所成角的取值范围为
D.与平面所成角的取值范围为
2.(2023·全国·模拟预测)如图①,四边形ABCD是两个直角三角形拼接而成,,,,.现沿着BD进行翻折,使平面平面BCD,连接AC,得到三棱锥(如图②),则下列选项中正确的是( )
A.平面平面ACD
B.二面角的大小为60°
C.异面直线AD与BC所成角的余弦值为
D.三棱锥外接球的表面积为
3.(2023·全国·模拟预测)如图1,矩形由正方形与拼接而成.现将图形沿对折成直二面角,如图2.点(不与重合)是线段上的一个动点,点在线段上,点在线段上,且满足,,则( )
图1 图2
A.B.
C.的最大值为D.多面体的体积为定值
三、填空题
1.(2023·河南·模拟预测)如图,在棱长为1 的正方体中,是棱 (不包含端点)上一动点,则三棱锥 的体积的取值范围为 .
2.(2023·江苏淮安·模拟预测)某同学参加课外航模兴趣小组活动,学习模型制作.将一张菱形铁片进行翻折,菱形的边长为1,,E是边上一点,将沿着DE翻折到位置,使平面面,则点A与之间距离最小值是 .
3.(23-24高三上·河北保定·期末)如图,在棱长为8的正方体中,是棱上的一个动点,给出下列三个结论:①若为上的动点,则的最小值为;②到平面的距离的最大值为;③为的中点,为空间中一点,且与平面所成的角为,与平面所成的角为,则在平面上射影的轨迹长度为,其中所有正确结论的序号是 .
四、解答题
1.(2023·河南·二模)如图所示,正六棱柱的底面边长为1,高为,为线段上的动点.
(1)求证:平面;
(2)设直线与平面所成的角为,求的取值范围.
2.(2024高三·全国·专题练习)如图,在正方体中,分别是、的中点.
(1)求与所成的角;
(2)设,在正方形内(或上),是否存在点使得三棱锥的体积为1?若存在,求出动点的轨迹;若不存在,说明理由.
3.(2023·广西南宁·模拟预测)如图,在矩形中,,,点是边上的动点,沿将翻折至,使二面角为直二面角.
(1)当时,求证:;
(2)当时,求二面角的正弦值.
4.(22-23高三下·安徽·阶段练习)如图,在四棱锥中,所有棱长都相等,,分别是棱,的中点,是棱上的动点,且.
(1)若,证明:平面.
(2)求平面与平面夹角余弦值的最大值.
5.(2023·全国·模拟预测)如图,在直三棱柱中,,,垂直于平面.点,,分别为边,,上的动点(不包括顶点),且满足.
(1)求三棱锥的体积的最大值;
(2)记平面与平面所成的锐二面角为,当最小时,求的值,并说明点所处的位置.
相关试卷
这是一份微重点07 球的切接问题(2大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用),文件包含微重点07球的切接问题2大考点+强化训练原卷版docx、微重点07球的切接问题2大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
这是一份微重点06子数列与增减项问题(3大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用),文件包含微重点06子数列与增减项问题3大考点+强化训练原卷版docx、微重点06子数列与增减项问题3大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份微重点05数列的递推关系(2大考点+强化训练)-冲刺985、211名校高考数学重难点培优全攻略(新高考专用),文件包含微重点05数列的递推关系2大考点+强化训练原卷版docx、微重点05数列的递推关系2大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。












