

2024年安徽省合肥市庐江县柯坦初级中学中考数学模拟试卷+
展开1.(4分)下列四个数中,最小的是( )
A.﹣3B.﹣3.5C.0D.|﹣5|
2.(4分)去年12月8日,2023世界新能源汽车大会“碳中和愿景下的全面电动化解决方案”论坛在我国海南国际会展中心隆重召开,随后,中国汽车工业协会发布了《2024中国汽车市场整体预测报告》.预测2024年中国新能源汽车销量将达1150万辆左右,1150万用科学记数法表示为( )
A.115×104B.115×105C.1.15×106D.1.15×107
3.(4分)下列运算正确的是( )
A.a2+a3=a5B.a2•a3=a6C.a8÷a2=a6D.(﹣a2)3=a6
4.(4分)下列四个几何体中,其主视图是轴对称图形但不是中心对称图形的是( )
A.B.C.D.
5.(4分)不等式组的解集在数轴上表示为( )
A.
B.
C.
D.
6.(4分)如图、AD,BE,CF分别是△ABC的中线、高和角平分线,∠ABC=90°,CF交AD于点G,交BE于点H,则下列结论一定正确的是( )
A.∠ABE=∠FCBB.∠GAC=∠GCAC.FG=GCD.BF=BH
7.(4分)某超市销售一种袋装大米,在包装袋上标有净重:25±0.25(kg).一次,主管部门对超市预销售的500袋这种大米进行重量检测,从中随机抽取了10袋,测得他们的重量如下(单位:kg,包装袋的重量已扣除):25.1,25.4,24.9,25.2,25.2,25.2,25.0,24.7,25.1,25.2,在这个问题中,下列说法正确的是( )
A.采用的调查方式是全面调查
B.总体中重量的达标率一定是80%
C.样本的中位数是25.2kg
D.样本的平均数是25.1kg
8.(4分)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,D为优弧BC上任意一点,若∠A=28°,则∠D=( )
A.62°B.59°C.56°D.45°
9.(4分)已知关于x的函数y=ax2﹣(a+1)x+(a﹣1)的图象与坐标轴共有两个不同的交点,则实数a的可能值有( )
A.4个B.3个C.2个D.1个
10.(4分)如图,▱ABCD的对角线AC,BD交于点O,E是AB边上的动点,连接OE,DE,DE交AO于点F.若AB=2BC=4,∠DAB=60°,则下列结论中错误的是( )
A.DE的最小值是
B.∠DEO总小于60°
C.当点E是AB的中点时,△EOF的面积是
D.△DOE周长的最小值是+3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)代数式有意义时,x应满足的条件为 .
12.(5分)因式分解:a3﹣a= .
13.(5分)如图,在平面直角坐标系xOy中,△OAB的边AB∥x轴,OA=AB,点B关于直线OA的对称点B′的坐标为,若反比例函数的图象经过点B.则k的值为 .
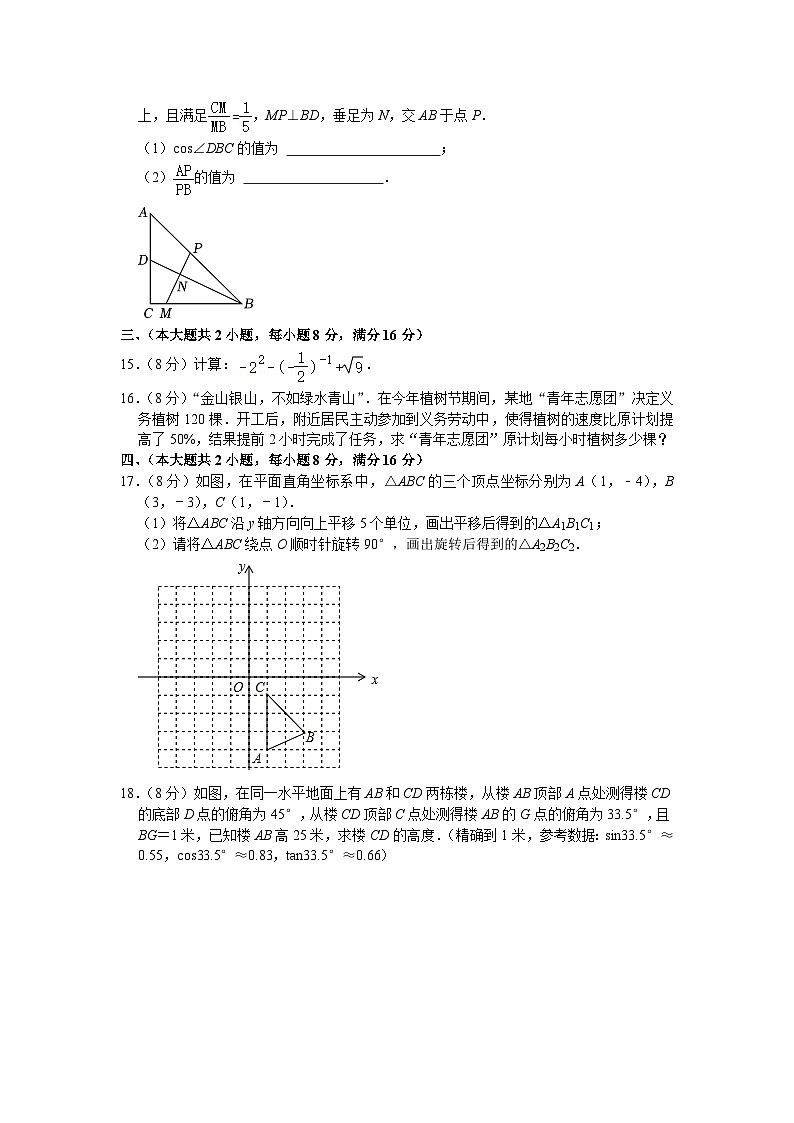
14.(5分)如图,在△ABC中,AC=BC,∠C=90°,点D为AC的中点,点M在BC边上,且满足,MP⊥BD,垂足为N,交AB于点P.
(1)cs∠DBC的值为 ;
(2)的值为 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)计算:.
16.(8分)“金山银山,不如绿水青山”.在今年植树节期间,某地“青年志愿团”决定义务植树120棵.开工后,附近居民主动参加到义务劳动中,使得植树的速度比原计划提高了50%,结果提前2小时完成了任务,求“青年志愿团”原计划每小时植树多少棵?
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣4),B(3,﹣3),C(1,﹣1).
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)请将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2.
18.(8分)如图,在同一水平地面上有AB和CD两栋楼,从楼AB顶部A点处测得楼CD的底部D点的俯角为45°,从楼CD顶部C点处测得楼AB的G点的俯角为33.5°,且BG=1米,已知楼AB高25米,求楼CD的高度.(精确到1米,参考数据:sin33.5°≈0.55,cs33.5°≈0.83,tan33.5°≈0.66)
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;……
(1)请你按照上述等式规律写出第5个等式;
(2)根据上述等式规律写出第n个等式;
(3)证明(2)中你所写等式的正确性.
20.(10分)已知AB是半径为r的⊙O的直径,C,D分别为⊙O上的两个动点(A,B两点除外,且在直径AB的同侧),CE⊥AB于点E,F是CD的中点.
(1)如图1,若CD∥AB,求证:EF=r;
(2)如图2,若CD不平行于AB,r=5,求EF的长的最大值.
六、(本题满分12分)
21.(12分)某校九年级举行了“爱我中华,学习强国”党史知识测试,并把成绩分成A、B、C、D四个等级,学校决定对成绩为D等级的学生分批进行培训.王老师随机抽取了一个班的成绩进行统计,并绘制了两幅不完整的统计图如图:
根据信息解答:
(1)填空:该班共有 名学生,扇形统计图中,C等级对应扇形的圆心角的度数为 ;
(2)若该校九年级一共有600名学生,估计该校九年级需要参加培训的学生有多少名?
(3)该班成绩为D等级的5名同学中,有2名是男生,3名是女生,从中任选两名参加第一批培训,请利用画树状图或列表法,求选中的两名同学恰好都是男生的概率.
七、(本题满分12分)
22.(12分)如图,在四边形ABCD中,AB∥CD,∠DAB=90°,O是BD的中点,AO的延长线交BC于点E,∠CBD=∠BAE.
(1)求证:BC=DC;
(2)若AE⊥BC,求证:BD2=4CD•BE.
八、(本题满分14分)
23.(14分)已知抛物线y=ax2+bx﹣3与y轴相交于点A(0,﹣3),与x轴相交于点B(1,0)和点C(3,0),直线l:y=kx+2k+3经过定点D.
(1)求a和b的值及点D的坐标;
(2)如图1,当k=﹣1时,位于直线l上方的抛物线上有一点P,过点P作PM∥y轴交直线l于点M,求PM的最大值;
(3)如图2,连接并延长AB,将射线AB绕点A顺时针旋转45°后,与抛物线相交于点E,求点E的坐标.
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A、B、C、D四个选项,其中只有一个是正确的。
1.(4分)下列四个数中,最小的是( )
A.﹣3B.﹣3.5C.0D.|﹣5|
【分析】根据两个负数比较,绝对值小的反而大,负数小于0,0小于正数,即可解答.
【解答】解:∵|﹣3|=3,|﹣3.5|=3.5,
∴3.5>3,
∴﹣3.5<﹣3,
∵|﹣5|=5,
∴在﹣3,﹣3.5,0,|﹣5|这四个数中,﹣3.5<﹣3<0<|﹣5|,
∴最小的是﹣3.5,
故选:B.
【点评】本题考查了有理数大小比较,绝对值,熟练掌握两个负数比较,绝对值小的反而大是解题的关键.
2.(4分)去年12月8日,2023世界新能源汽车大会“碳中和愿景下的全面电动化解决方案”论坛在我国海南国际会展中心隆重召开,随后,中国汽车工业协会发布了《2024中国汽车市场整体预测报告》.预测2024年中国新能源汽车销量将达1150万辆左右,1150万用科学记数法表示为( )
A.115×104B.115×105C.1.15×106D.1.15×107
【分析】用科学记数法表示数,一定要注意a的形式,以及指数n的确定方法.
【解答】解:1150万=11500000,用科学记数法表示为1.15×107.
故选:D.
【点评】本题考查用科学记数法表示较大的数,掌握形式为a×10n,其中1≤|a|<10,n可以用整数位数减去1来确定是关键.
3.(4分)下列运算正确的是( )
A.a2+a3=a5B.a2•a3=a6C.a8÷a2=a6D.(﹣a2)3=a6
【分析】根据同底数幂的乘除法法则、合并同类项和幂的乘方与积的乘方法则进行逐项判断即可.
【解答】解:A、a3与a2不是同类项,故不能进行合并,不符合题意;
B、a3•a2=a5,故该项不正确,不符合题意;
C、a8÷a2=a6,故该项正确,符合题意;
D、(﹣a2)3=﹣a6,故该项不正确,不符合题意;
故选:C.
【点评】本题考查同底数幂的乘除法、合并同类项和幂的乘方与积的乘方,熟练掌握相关的知识点是解题的关键.
4.(4分)下列四个几何体中,其主视图是轴对称图形但不是中心对称图形的是( )
A.B.C.D.
【分析】根据简单几何体的主视图的性质结合轴对称图形,中心对称图形的定义进行判断即可.
【解答】解:A.圆锥体的主视图是等腰三角形,等腰三角形是轴对称图形但不是中心对称图形,因此选项A符合题意;
B.正方体的主视图是正方形,正方形既是是轴对称图形,又是中心对称图形,因此选项B不符合题意;
C.圆柱体的主视图是长方形,长方形既是是轴对称图形,又是中心对称图形,因此选项C不符合题意;
D.球体的主视图是圆,圆既是是轴对称图形,又是中心对称图形,因此选项D不符合题意.
故选:A.
【点评】本题考查简单几何体的三视图,理解视图的定义,掌握简单几何体主视图的形状以及中心对称图形、轴对称图形的定义是正确解答的关键.
5.(4分)不等式组的解集在数轴上表示为( )
A.
B.
C.
D.
【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
【解答】解:
解①得:x>﹣3,
解②得:x≤2,
故不等式的解集为:﹣3<x≤2,
在数轴上表示为:
故选:C.
【点评】此题考查了一元一次不等式组的解法,不等式组取解集的方法为:同大取大;同小取小;大小小大去中间;大大小小无解.
6.(4分)如图、AD,BE,CF分别是△ABC的中线、高和角平分线,∠ABC=90°,CF交AD于点G,交BE于点H,则下列结论一定正确的是( )
A.∠ABE=∠FCBB.∠GAC=∠GCAC.FG=GCD.BF=BH
【分析】根据三角形的角平分线、中线和高的概念、直角三角形的性质、三角形中位线定理判断即可.
【解答】解:A、∵∠ABC=90°,
∴∠ABE+∠EBC=90°,
∵∠BEC=90°,
∴∠ACB+∠EBC=90°,
∴∠ABE=∠ACB>∠FCB,故本选项说法错误,不符合题意;
B、当△ABC为等腰直角三角形时,AB≠AC,
∵AD是中线,
∴AD不是角平分线,
∴∠GAC≠∠GCA,故本选项说法错误,不符合题意;
C、∵AD是△ABC的中线,
∴BD=DC,
当FG=GC时,DG是△CBF的中位线,
则GD∥BF,故本选项说法错误,不符合题意;
D、∵∠ACF=∠BCF,∠BFC=90°﹣∠BCF,∠BHF=∠EHC=90°﹣∠ACF,
∴∠BFC=∠BHF,
∴BF=BH,故本选项说法正确,符合题意;
故选:D.
【点评】本题考查的是三角形的角平分线、中线和高,掌握三角形的角平分线、中线和高的概念是解题的关键.
7.(4分)某超市销售一种袋装大米,在包装袋上标有净重:25±0.25(kg).一次,主管部门对超市预销售的500袋这种大米进行重量检测,从中随机抽取了10袋,测得他们的重量如下(单位:kg,包装袋的重量已扣除):25.1,25.4,24.9,25.2,25.2,25.2,25.0,24.7,25.1,25.2,在这个问题中,下列说法正确的是( )
A.采用的调查方式是全面调查
B.总体中重量的达标率一定是80%
C.样本的中位数是25.2kg
D.样本的平均数是25.1kg
【分析】根据全面调查与抽样调查、样本估计总体、中位数的概念、平均数的计算公式计算,判断即可.
【解答】解:A、采用的调查方式是抽样调查,故本选项说法错误,不符合题意;
B、总体中重量的达标率大约是80%,而不是一定是80%,故本选项说法错误,不符合题意;
C、样本的中位数是25.15kg,故本选项说法错误,不符合题意;
D、样本的平均数为:(25.1+25.4+24.9+25.2+25.2+25.2+25.0+24.7+25.1+25.2)=25.1(kg),本选项说法正确,符合题意;
故选:D.
【点评】本题考查的是中位数、平均数、全面调查与抽样调查以及样本估计总体,掌握相关的概念是解题的关键.
8.(4分)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,D为优弧BC上任意一点,若∠A=28°,则∠D=( )
A.62°B.59°C.56°D.45°
【分析】连接OB,由切线的性质求得∠ABO=90°,则∠BOC=∠A+∠ABO=118°,所以∠D=∠BOC=59°,于是得到问题的答案.
【解答】解:连接OB,
∵AB与⊙O相切于点B,
∴AB⊥OB,
∴∠ABO=90°,
∵∠A=28°,
∴∠BOC=∠A+∠ABO=28°+90°=118°,
∴∠D=∠BOC=×118°=59°,
故选:B.
【点评】此题重点考查圆周角定理、切线的性质定理、三角形的一个外角等于与它不相邻的两个内角的和等知识,正确地作出辅助线是解题的关键.
9.(4分)已知关于x的函数y=ax2﹣(a+1)x+(a﹣1)的图象与坐标轴共有两个不同的交点,则实数a的可能值有( )
A.4个B.3个C.2个D.1个
【分析】根据函数的图象与两坐标轴共有两个交点,可知该函数可能为一次函数,也可能为二次函数,然后分类讨论即可求得a的值,本题得以解决.
【解答】解:∵函数y=ax2﹣(a+1)x+(a﹣1)的图象与坐标轴共有两个不同的交点,
∴当a=0时,此时y=﹣x﹣1与两坐标轴两个交点,
当a≠0时,则或,
解得,a=或a=1,
由上可得,a的值是0,或1,共4个.
故选:A.
【点评】本题考查抛物线与x轴的交点、根的判别式、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质和分类讨论的思想解答.
10.(4分)如图,▱ABCD的对角线AC,BD交于点O,E是AB边上的动点,连接OE,DE,DE交AO于点F.若AB=2BC=4,∠DAB=60°,则下列结论中错误的是( )
A.DE的最小值是
B.∠DEO总小于60°
C.当点E是AB的中点时,△EOF的面积是
D.△DOE周长的最小值是+3
【分析】由题可证△ADB是直角三角形,A.当DE⊥AB时,DE取最小值,可得DE的 最小值是3;B.如图1,过点O作OG⊥BD交AB于G,连接DG,易知∠DGO=60°.以DG为直径画⊙P交AB于点H,当E与G或H重合时,∠DEO=60°,当点E在线段GH上(不含端点),∠DEO大于 60°;C.易得▱ABCD 的面积为 ,当E是AB的中点时,△AOE的面积为 ,OE∥AD,则,可得△EOF的面积是为 ;D.如图2,作D关于AB 的对称点D′,连接OD′,交AB于E,此时△DOE 的周长取最小值,,∠ADD'=∠AD'D=30°,则∠ODD'=60°,推出∠DOD'=90°,OD'=DD'•sin60°=3,此时△DOE 的周长=.
【解答】解:由题可知△ADB是直角三角形,,
A.当DE⊥AB时,DE取最小值,可得DE的 最小值是3;
B.如图1,过点O作OG⊥BD交AB于G,
连接DG,则∠DGO=60°.
以DG为直径画⊙P交AB于点H,
当E与G或H重合时,∠DEO=60°,
当点E在线段GH上(不含端点),∠DEO大于60°;
C.易得▱ABCD的面积为 ,
当E是AB的中点时,△AOE的面积为 ,OE∥AD,
∴,
可得△EOF的面积是为 ;
D.如图2,作D关于AB 的对称点D′,
连接OD′,交AB于E,此时△DOE的周长取最小值,,∠ADD'=∠AD'D=30°,
∴∠ODD'=60°,
∴∠DOD'=90°,OD'=DD'•sin60°=3,
此时△DOE 的周长=.
故选:B.
【点评】本题考查了轴对称﹣最短路线问题,三角形的面积.平行四边形的性质,解题的关键是掌握相关知识的灵活运用.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)代数式有意义时,x应满足的条件为 x≥0且x≠1 .
【分析】根据二次根式有意义时被开方数为非负数,分式有意义时分母不为零可求解x的取值范围.
【解答】解:由题意得,
解得:x≥0且x≠1.
故答案为:x≥0且x≠1.
【点评】本题主要考查二次根式有意义的条件及分式有意义的条件,根据二次根式及分式有意义的条件求解是解题的关键.
12.(5分)因式分解:a3﹣a=a(a+1)(a﹣1) .
【分析】原式提取a,再利用平方差公式分解即可.
【解答】解:原式=a(a2﹣1)=a(a+1)(a﹣1),
故答案为:a(a+1)(a﹣1)
【点评】此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
13.(5分)如图,在平面直角坐标系xOy中,△OAB的边AB∥x轴,OA=AB,点B关于直线OA的对称点B′的坐标为,若反比例函数的图象经过点B.则k的值为 .
【分析】过点B作x轴的垂线,根据轴对称的性质求出点B的坐标即可解决问题.
【解答】解:过点B作x轴的垂线,垂足为M,
因为点B和点B′关于OA对称,
所以∠B′OA=∠BOA,OB=OB′.
因为AO=AB,
所以∠AOB=∠ABO,
又因为AB∥x轴,
所以∠ABO=∠BOM,
所以∠AOB=∠BOM,
所以∠B′OA=∠AOB=∠BOM=30°.
因为点B′的坐标为,
所以OB=OB′=.
在Rt△BOM中,
sin30°=,
所以BM=,
所以OM=,
则点B的坐标为(3,).
将点B坐标代入y=得,
k=.
故答案为:.
【点评】本题考查反比例函数图象上点的坐标特征及坐标与图形变化﹣对称,熟知反比例函数的图象和性质及轴对称的性质是解题的关键.
14.(5分)如图,在△ABC中,AC=BC,∠C=90°,点D为AC的中点,点M在BC边上,且满足,MP⊥BD,垂足为N,交AB于点P.
(1)cs∠DBC的值为 ;
(2)的值为 .
【分析】(1)设CM=a,则BM=5a,根据勾股定理求出BD=3a,再根据余弦定义求解即可;
(2)延长PM,交AC的延长线于点E,过点A作AF∥BC交MP的延长线于点F,结合直角三角形的性质求出∠DBC=∠E,∠ECM=∠BCD=90°,则△EMC∽△BDC,根据相似三角形的性质得出=,设CM=a,则BM=5a,CD=3a,根据比例的性质求出CE=2a,根据平行线的性质推出△ECM∽△EAF,△AFP∽△BMP,根据相似三角形的性质等量代换求解即可.
【解答】解:(1)设CM=a,则BM=5a,
∴BC=CM+BM=6a,
∵AC=BC,
∴AC=6a,
∵点D为AC的中点,
∴CD=3a,
∵∠C=90°,
∴BD==3a,
∴cs∠DBC===,
故答案为:;
(2)如图,延长PM,交AC的延长线于点E,过点A作AF∥BC交MP的延长线于点F,
∵∠ACB=90°,MP⊥BD于N,
∴∠BDC+∠DBC=90°,∠BDC+∠E=90°,
∴∠DBC=∠E,
又∵∠ECM=∠BCD=90°,
∴△EMC∽△BDC,
∴=,
设CM=a,则BM=5a,CD=3a,
∴=,
∴CE=2a,
∵AF∥BC,
∴△ECM∽△EAF,△AFP∽△BMP,
∴===,=,
∴AF=4a,
∴==,
故答案为:.
【点评】此题考查了相似三角形的判定与性质,熟记相似三角形的判定与性质是解题的关键.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)计算:.
【分析】先计算二次根式、负整数指数幂和平方,再计算加减.
【解答】解:
=﹣4+2+3
=1.
【点评】此题考查了实数的混合运算能力,关键是能准确确定运算顺序,并能进行正确地计算.
16.(8分)“金山银山,不如绿水青山”.在今年植树节期间,某地“青年志愿团”决定义务植树120棵.开工后,附近居民主动参加到义务劳动中,使得植树的速度比原计划提高了50%,结果提前2小时完成了任务,求“青年志愿团”原计划每小时植树多少棵?
【分析】设“青年志愿团”原计划每小时植树x棵,根据开工后,附近居民主动参加到义务劳动中,使得植树的速度比原计划提高了50%,结果提前2小时完成了任务,列出分式方程,解方程即可.
【解答】解:设“青年志愿团”原计划每小时植树x棵,
由题意得:﹣=2,
解得:x=20,
经检验,x=20是原方程的解,且符合题意,
答:“青年志愿团”原计划每小时植树20棵.
【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣4),B(3,﹣3),C(1,﹣1).
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)请将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2.
【分析】(1)利用点平移的规律写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A2、B2、C2,从而得到△A2B2C2.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求.
【点评】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.
18.(8分)如图,在同一水平地面上有AB和CD两栋楼,从楼AB顶部A点处测得楼CD的底部D点的俯角为45°,从楼CD顶部C点处测得楼AB的G点的俯角为33.5°,且BG=1米,已知楼AB高25米,求楼CD的高度.(精确到1米,参考数据:sin33.5°≈0.55,cs33.5°≈0.83,tan33.5°≈0.66)
【分析】过点C作CF⊥AB,垂足为F,根据题意可得:CD=BF,CF=BD,AB⊥BD,AE∥BD,从而可得∠EAD=∠ADB=45°,然后在Rt△ABD中,利用锐角三角函数的定义求出BD长,从而在Rt△CFG中,利用锐角三角函数的定义求出FG的长,最后利用线段的和差关系进行计算,即可解答.
【解答】解:如图:过点C作CF⊥AB,垂足为F,
由题意得:CD=BF,CF=BD,AB⊥BD,AE∥BD,
∴∠EAD=∠ADB=45°,
在Rt△ABD中,AB=25米,
∴BD==25(米),
∴CF=BD=25米,
在Rt△CFG中,∠FCG=33.5°,
∴FG=CF•tan33.5°≈25×0.66=16.5(米),
∵BG=1米,
∴CD=BF=BG+FG=1+16.5≈18(米),
∴楼CD的高度约为18米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;……
(1)请你按照上述等式规律写出第5个等式;
(2)根据上述等式规律写出第n个等式;
(3)证明(2)中你所写等式的正确性.
【分析】(1)根据前几个等式,可得第5个等式:=;
(2)第n个等式:=;
(3)证明等式左边等于等式右边即可.
【解答】解:(1)=;
(2)=;
(3)∵左边=====右边,
∴等式成立.
【点评】本题考查的是数字的变化规律,从题目中找出数字的变化规律是解题的关键.
20.(10分)已知AB是半径为r的⊙O的直径,C,D分别为⊙O上的两个动点(A,B两点除外,且在直径AB的同侧),CE⊥AB于点E,F是CD的中点.
(1)如图1,若CD∥AB,求证:EF=r;
(2)如图2,若CD不平行于AB,r=5,求EF的长的最大值.
【分析】(1)连接OF、OC,证明四边形OECF是矩形即可解答;
(2)延长CE交⊙O于点G,连接DG,首先证明点E是CG的中点,得出EF=DG,进而在DG取得最大值时求出EF的最大值.
【解答】( 1)证明:如图1,连接OF,OC,
∵CE⊥AB,
∴∠CEO=90°,
∵CD∥AB,
∴∠ECD=90°=∠CEO,
∵F是CD的中点,
∴OF⊥CD,
∴∠OFC=90°,
∴四边形OECF是矩形,
∴EF=OC=r;
(2)解:如图2,延长CE交⊙O于点G,连接DG,
∵AB是半径为r的⊙O的直径,AB⊥CG于点E,
∴E是CG的中点,
又∵F是CD的中点,
∴EF=DG,
又∵DG的最大值为2r=10,
∴EF的长的最大值是5.
【点评】本题考查圆周角定理,三角形的中位线定理,矩形的判定等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.
六、(本题满分12分)
21.(12分)某校九年级举行了“爱我中华,学习强国”党史知识测试,并把成绩分成A、B、C、D四个等级,学校决定对成绩为D等级的学生分批进行培训.王老师随机抽取了一个班的成绩进行统计,并绘制了两幅不完整的统计图如图:
根据信息解答:
(1)填空:该班共有 40 名学生,扇形统计图中,C等级对应扇形的圆心角的度数为 99° ;
(2)若该校九年级一共有600名学生,估计该校九年级需要参加培训的学生有多少名?
(3)该班成绩为D等级的5名同学中,有2名是男生,3名是女生,从中任选两名参加第一批培训,请利用画树状图或列表法,求选中的两名同学恰好都是男生的概率.
【分析】(1)根据A等级的人数以及占比即可求出参加知识测试的总人数;先求出C等级的人数,然后根据C等级人数得占比即可求出对应的圆心角度数.
(2)用总人数乘以样本中D等级的人数占比即可求出答案.
(3)画树状图,共有20种等可能的结果,再由概率公式求解即可.
【解答】解:(1)该班的学生数为:8÷20%=40(名),
C等级的人数为:40﹣8﹣16﹣5=11(名),
C等级对应扇形的圆心角的度数为:360°×=99°.
故答案为:40,99°;
(2)600×=75(名),
估计该校九年级需要参加培训的学生有75名;
(3)根据题意画图如下:
共有20种等可能的结果,被选中的两名学生恰好都是男生的结果有2种,
∴被选中的两名学生恰好都是男生的概率为.
【点评】本题考查概率与统计综合,涉及扇形统计图与条形统计图数据关联、补全条形统计图、用样本估计总体及列举法求概率等知识.
七、(本题满分12分)
22.(12分)如图,在四边形ABCD中,AB∥CD,∠DAB=90°,O是BD的中点,AO的延长线交BC于点E,∠CBD=∠BAE.
(1)求证:BC=DC;
(2)若AE⊥BC,求证:BD2=4CD•BE.
【分析】(1)根据直角三角形的性质及等腰三角形的性质求出∠BAE=∠OBA,等量代换得出∠CBD=∠OBA,结合平行线的性质求出∠CDB=∠CBD,根据等腰三角形的判定即可得解;
(2)根据等腰三角形的性质得出∠COD=90°,根据“两角对应相等的两个三角形相似”求出△COD∽△OEB,根据相似三角形的性质即可得解.
【解答】证明:(1)∵∠DAB=90°,O是BD的中点,
∴OA=OB,
∴∠BAE=∠OBA,
∵∠CBD=∠BAE,
∴∠CBD=∠OBA,
∵AB∥CD,
∴∠CDB=∠OBA,
∴∠CDB=∠CBD,
∴BC=CD;
(2)如图,连接OC,
∵BC=CD,O是BD的中点,
∴OC⊥BD,
∴∠COD=90°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠COD=∠AEB,
由(1)知,∠CDB=∠CBD,
∴△COD∽△OEB,
∴=,
∴OD•OB=CD•BE,
∵O是BD的中点,
∴OD=OB=BD,
∴BD2=CD•BE,
∴BD2=4CD•BE.
【点评】此题考查了相似三角形的判定与性质,直角三角形斜边上的中线性质,根据直角三角形斜边上的中线性质求出OA=OB是解题的关键.
八、(本题满分14分)
23.(14分)已知抛物线y=ax2+bx﹣3与y轴相交于点A(0,﹣3),与x轴相交于点B(1,0)和点C(3,0),直线l:y=kx+2k+3经过定点D.
(1)求a和b的值及点D的坐标;
(2)如图1,当k=﹣1时,位于直线l上方的抛物线上有一点P,过点P作PM∥y轴交直线l于点M,求PM的最大值;
(3)如图2,连接并延长AB,将射线AB绕点A顺时针旋转45°后,与抛物线相交于点E,求点E的坐标.
【分析】(1)由待定系数法求出函数表达式,由y=kx+2k+3=k(x+2)+3,即可求解;
(2)由PM=﹣x2+4x﹣3﹣(﹣x+1)=﹣(x﹣2.5)2+2.25≤2.25,即可求解;
(3)证明△TNB≌△AMT(AAS),则BN=TM且NT=AM,求取T(2,﹣2),进而求解.
【解答】解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2),
则y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=ax2+bx﹣3,
则3a=﹣3,
则a=﹣1,
则抛物线的表达式为:y=﹣x2+4x﹣3;
∵y=kx+2k+3=k(x+2)+3,
则点D(﹣2,3);
(2)当k=﹣1时,直线l的表达式为:y=﹣x+1,如题干图,
设点P(x,﹣x2+4x﹣3),则点M(x,﹣x+1),
则PM=﹣x2+4x﹣3﹣(﹣x+1)=﹣(x﹣2.5)2+2.25≤2.25,
故PM的最大值为2.25;
(3)过点B作BT⊥AE于点T(x,y),
∵∠BAE=45°,则△ABT为等腰直角三角形,
则AT=BT,
过点T作x轴的垂线交x轴于点N,交点A和x轴的平行线于点M,
∵∠BTN+∠ATM=90°,∠ATM+∠MAT=90°,
∴∠BTN=∠MAT,
∵∠TNB=∠AMT=90°,
∴△TNB≌△AMT(AAS),
则BN=TM且NT=AM,
即x﹣1=y+3且﹣y=x,
解得:x=2=﹣y,
即点T(2,﹣2),
由点A、T的坐标得,直线AT的表达式为:y=x﹣3,
将上式和抛物线的表达式联立得:﹣x2+4x﹣3=x﹣3,
解得:x=0(舍去)或,
则点E(,﹣).
【点评】本题考查的是二次函数综合运用,涉及到三角形全等、函数过定点、线段长度的表示方法等,有一定的综合性,难度适中.
安徽省合肥市庐江县+柯坦初级中学2023-2024学年八年级下学期月考数学试题: 这是一份安徽省合肥市庐江县+柯坦初级中学2023-2024学年八年级下学期月考数学试题,共7页。试卷主要包含了下列计算正确的是,刘老师在黑板上写了一个式子,已知,,则等内容,欢迎下载使用。
【中考模拟】2023年安徽省合肥市庐江县庐州学校初中毕业班中考数学模拟试题(含答案): 这是一份【中考模拟】2023年安徽省合肥市庐江县庐州学校初中毕业班中考数学模拟试题(含答案),共29页。试卷主要包含了0分等内容,欢迎下载使用。
精品解析:2023年安徽省合肥市庐江县庐州学校中考数学模拟试卷: 这是一份精品解析:2023年安徽省合肥市庐江县庐州学校中考数学模拟试卷,文件包含精品解析2023年安徽省合肥市庐江县庐州学校中考数学模拟试卷解析版docx、精品解析2023年安徽省合肥市庐江县庐州学校中考数学模拟试卷原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。












