北师大版九年级数学全册高分突破必练专题专项35圆中利用转化思想求角度(原卷版+解析)

这是一份北师大版九年级数学全册高分突破必练专题专项35圆中利用转化思想求角度(原卷版+解析)，共28页。

类型一 利用同弧或等弧转化圆周角与圆心角
类型二 构造圆内接四边形转化角
类型三 利用直径构造直角三角形转化角
类型四 利用特殊数量关系构造特殊角转化角
【考点1 利用同弧或等弧转化圆周角与圆心角】
【典例1】（2022秋•二道区校级期末）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝25°，则∠BDC＝（ ）
A．55°B．60°C．65°D．70°
【变式1-1】（2022秋•屯留区期末）如图，点A，B，C在⊙O上，∠BAC＝40°，连接OB，OC，则∠BOC的度数是（ ）
A．60°B．70°C．75°D．80°
【变式1-2】（2022秋•靖江市期末）如图，AB是⊙O直径，∠BOC＝40°，则∠D为（ ）
A．40°B．30°C．20°D．70°
【考点2 构造圆内接四边形转化角】
【典例2】（2021九上·哈尔滨月考）如图，四边形ABCD内接于 ⊙O ，如果它的一个外角 ∠DCE=64° ，那么 ∠BOD 的度数为（ ）
A．64°B．128°C．20°D．116°
【变式2-1】（2022秋•泰山区校级期末）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为劣弧BD的中点，若∠DAB＝60°，则∠ABC的度数是（ ）
A．70°B．40°C．60°D．50°
【变式2-2】（2022秋•番禺区校级期末）如图，四边形ABCD是⊙O的内接四边形，其中∠A＝100°，则∠C的度数为（ ）
A．120°B．100°C．80°D．50°
【变式2-3】（2022秋•未央区校级期末）如图，AB是半圆O的直径，点D是弧AC的中点，若∠BAC＝44°，则∠DAC等于（ ）
A．22°B．44°C．23°D．46°
【考点3 利用直径构造直角三角形转化角】
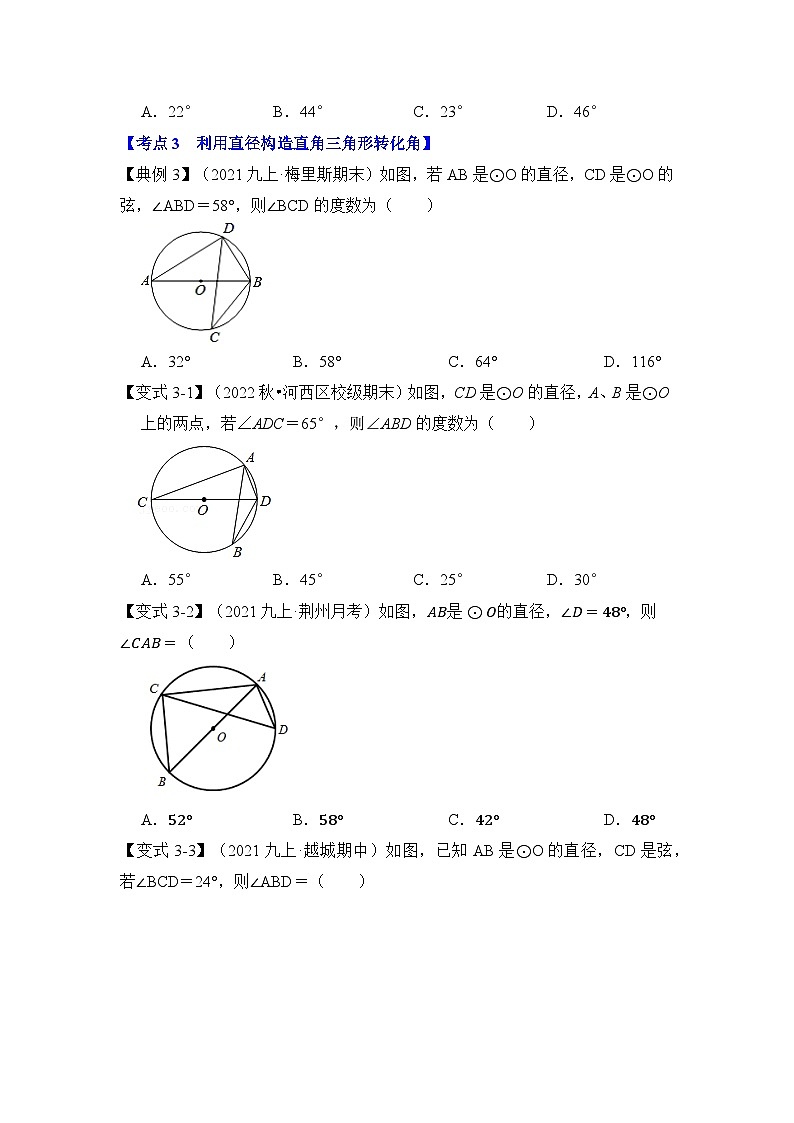
【典例3】（2021九上·梅里斯期末）如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝58°，则∠BCD的度数为（ ）
A．32°B．58°C．64°D．116°
【变式3-1】（2022秋•河西区校级期末）如图，CD是⊙O的直径，A、B是⊙O上的两点，若∠ADC＝65°，则∠ABD的度数为（ ）
A．55°B．45°C．25°D．30°
【变式3-2】（2021九上·荆州月考）如图，AB是⊙O的直径，∠D=48°，则∠CAB=（ ）
A．52°B．58°C．42°D．48°
【变式3-3】（2021九上·越城期中）如图，已知AB是⊙O的直径，CD是弦，若∠BCD＝24°，则∠ABD＝（ ）
A．54°B．56°C．64°D．66°
【考点4 利用特殊数量关系构造特殊角转化角】
【典例4】（2018•石家庄模拟）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r＝5，AC＝5，则∠B的度数是（ ）
A．30°B．45°C．50°D．60°
【变式4】（2021秋•无为市期中）如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧AMB上一点，则∠APB的度数为（ ）
A．45°B．30°C．75°D．60°
1．（2022秋•重庆期末）如图，AB是⊙O的直径，点C、D在⊙O上，若∠AOD＝130°，则∠C的度数是（ ）
A．35°B．30°C．25°D．20°
2．（2023•惠阳区校级开学）如图所示，四边形ABCD为⊙O的内接四边形，∠BCD＝120°，则∠BOD的大小是（ ）
A．60°B．110°C．120°D．90°
3．（2022秋•西安期末）如图，AB、CD为⊙O的两条弦，⊙O的半径为r，AB＝r，CD＝r，连接AC、BD，AC与BD交于点H，则∠BHC的度数为（ ）
A．100°B．105°C．110°D．115°
4．（2022秋•运城期末）如图所示，AB、CD是⊙O的两条互相垂直的弦，圆心角∠AOC＝140°，AD、CB的延长线相交于P，则∠P＝（ ）°．
A．40B．50C．60D．70
5．（2022秋•碑林区校级期末）如图，AB是半圆的直径，点C和D都在半圆上，已知∠ABC＝25°，那么∠CDB的度数为（ ）
A．140°B．115°C．110°D．120°
6．（2022秋•南关区校级期末）如图，在边长为1的正方形网格中，点A，B，D在格点上，以AB为直径的圆过C，D两点，则cs∠BCD的值为（ ）
A．B．C．D．
7．（2022秋•任城区校级期末）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝35°，则∠AOB的大小为（ ）
A．10°B．20°C．35°D．40°
8．（2022秋•江津区期末）如图，AB是⊙O的弦，半径OC⊥AB于点D，∠P＝26°，点P在圆周上，则∠A等于（ ）
A．26°B．30°C．34°D．38°
9．（2022秋•任城区校级期末）如图，点A，B，C在⊙O上，点D是AB延长线上一点，若∠AOC＝100°，则∠CBD的度数为（ ）
A．50°B．52.5°C．55°D．60°
10．（2022秋•历下区期末）如图，AB为⊙O的直径，C，D为⊙O上的两点，若∠ACD＝56°，则∠DAB的度数为（ ）
A．34°B．36°C．46°D．54°
11．（2022秋•郾城区校级期末）如图，⊙O的半径为3，将⊙O的一部分沿着弦AB翻折，劣弧恰好经过圆心O，则折痕AB的长为（ ）
A．1B．2C．D．
12．（2022秋•红桥区校级期末）如图，MN是⊙O的直径，A，B，C是⊙O上的三点，∠ACM＝60°，B点是的中点，P点是MN上一动点，若⊙O的半径为1，则PA+PB的最小值为（ ）
A．1B．C．D．﹣1
13．（2023•市南区一模）如图，四边形ABCD内接于⊙O，F是上一点，且＝，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC＝105°，∠BAC＝25°，则∠E的度数为（ ）
A．60°B．55°C．50°D．45°
14．（2022秋•桥西区校级期末）如图，四边形ABCD内接于⊙O，∠ABC＝135°，AC＝4．
（1）∠AOC的度数为 ；
（2）⊙O的半径为 ．
15．（2022秋•榆树市期末）如图，点A，B，C在⊙O上，若∠ABC＝130°，则∠AOC的度数是 ．
16.（2022•曲周县模拟）如图，AB是⊙O的直径，点C在⊙O上，CD平分∠ACB交⊙O于点D，若∠ABC＝30°，则∠CAD的度数为（ ）
A．100°B．105°C．110°D．120
专项35 圆中利用转化思想求角度
类型一 利用同弧或等弧转化圆周角与圆心角
类型二 构造圆内接四边形转化角
类型三 利用直径构造直角三角形转化角
类型四 利用特殊数量关系构造特殊角转化角
【考点1 利用同弧或等弧转化圆周角与圆心角】
【典例1】（2022秋•二道区校级期末）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝25°，则∠BDC＝（ ）
A．55°B．60°C．65°D．70°
【答案】C
【解答】解：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵∠ABC＝25°，
∴∠CAB＝65°，
∴∠BDC＝∠CAB＝65°，
故选：C．
【变式1-1】（2022秋•屯留区期末）如图，点A，B，C在⊙O上，∠BAC＝40°，连接OB，OC，则∠BOC的度数是（ ）
A．60°B．70°C．75°D．80°
【答案】D
【解答】解：∵∠BAC和∠BOC是同弧所对的圆周角和圆心角，∠BAC＝40°，
∴∠BOC＝2∠BAC＝80°．
故选：D．
【变式1-2】（2022秋•靖江市期末）如图，AB是⊙O直径，∠BOC＝40°，则∠D为（ ）
A．40°B．30°C．20°D．70°
【答案】C
【解答】解：∵∠BOC＝40°，
∴∠D＝∠BOC＝×40°＝20°．
故选：C．
【考点2 构造圆内接四边形转化角】
【典例2】（2021九上·哈尔滨月考）如图，四边形ABCD内接于 ⊙O ，如果它的一个外角 ∠DCE=64° ，那么 ∠BOD 的度数为（ ）
A．64°B．128°C．20°D．116°
【答案】B
【解答】∵四边形ABCD内接于 ⊙O
∴∠BAD+∠DCB=180°
∵∠DCE+∠DCB=180°
∴∠BAD=∠DCE=64°
∵∠BOD、∠BAD对着圆中同一段弧
∴∠BOD=2∠BAD=2×64°=128°
故答案为：B
【变式2-1】（2022秋•泰山区校级期末）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为劣弧BD的中点，若∠DAB＝60°，则∠ABC的度数是（ ）
A．70°B．40°C．60°D．50°
【答案】C
【解答】解：连接AC，
∵点C为劣弧BD的中点，∠DAB＝60°，
∴∠CAB＝∠DAB＝30°，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠ABC＝90°﹣30°＝60°，
故选：C．
【变式2-2】（2022秋•番禺区校级期末）如图，四边形ABCD是⊙O的内接四边形，其中∠A＝100°，则∠C的度数为（ ）
A．120°B．100°C．80°D．50°
【答案】C
【解答】解：∵四边形ABCD为圆内接四边形，
∴∠A+∠C＝180°，
∵∠A＝100°，
∴∠C＝180°﹣∠A＝180°﹣100°＝80°．
故选：C．
【变式2-3】（2022秋•未央区校级期末）如图，AB是半圆O的直径，点D是弧AC的中点，若∠BAC＝44°，则∠DAC等于（ ）
A．22°B．44°C．23°D．46°
【答案】C
【解答】解：∵AB是半圆O的直径，
∴∠ACB＝90°，
∵∠BAC＝44°，
∴∠B＝90°﹣∠BAC＝46°，
∵四边形ABCD是半⊙O的内接四边形，
∴∠D＝180°﹣∠B＝134°，
∵点D是弧AC的中点，
∴＝，
∴AD＝DC，
∴∠DAC＝∠DCA＝（180°﹣∠D）＝23°，
故选：C．
【考点3 利用直径构造直角三角形转化角】
【典例3】（2021九上·梅里斯期末）如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝58°，则∠BCD的度数为（ ）
A．32°B．58°C．64°D．116°
【答案】A
【解答】解：∵AB是⊙O的直径，
∴∠ADB＝90°．
∵∠ABD＝58°，
∴∠A＝90°﹣58°＝32°，
∴∠BCD＝∠A＝32°．
故答案为：A．
【变式3-1】（2022秋•河西区校级期末）如图，CD是⊙O的直径，A、B是⊙O上的两点，若∠ADC＝65°，则∠ABD的度数为（ ）
A．55°B．45°C．25°D．30°
【答案】C
【解答】解：∵CD是⊙O的直径，
∴∠CAD＝90°，
∴∠C＝∠ABD＝90°﹣∠ADC＝90°﹣65°＝25°．
故选：C．
【变式3-2】（2021九上·荆州月考）如图，AB是⊙O的直径，∠D=48°，则∠CAB=（ ）
A．52°B．58°C．42°D．48°
【答案】C
【解答】解：∵AB是⊙O的直径，
∴∠ACB=90°，
∵∠D=48°，
∴∠ABC=48°，
∴∠CAB=90°−48°=42°，
故答案为：C.
【变式3-3】（2021九上·越城期中）如图，已知AB是⊙O的直径，CD是弦，若∠BCD＝24°，则∠ABD＝（ ）
A．54°B．56°C．64°D．66°
【答案】D
【解答】解：∵AB是⊙O的直径，
∴∠ADB＝90°，∠A＝∠BCD＝24°，
∴∠ABD＝90°﹣∠A＝90°﹣24°＝66°.
故答案为：D.
【考点4 利用特殊数量关系构造特殊角转化角】
【典例4】（2018•石家庄模拟）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r＝5，AC＝5，则∠B的度数是（ ）
A．30°B．45°C．50°D．60°
【答案】D
【解答】解：∵AD是⊙O的直径，
∴∠ACD＝90°．
Rt△ACD中，AD＝2r＝10，AC＝5．
根据勾股定理，得：CD＝＝5，
∴CD＝AD，
∴∠DAC＝30°，
∴∠B＝∠D＝90°﹣30°＝60°；
故选：D．
【变式4】（2021秋•无为市期中）如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧AMB上一点，则∠APB的度数为（ ）
A．45°B．30°C．75°D．60°
【答案】D
【解答】解：连接OA，OB，过O作OD⊥AB于D，延长OD交⊙O于C，则∠ODA＝∠ODB＝90°，
∵将⊙O沿弦AB折叠，圆弧恰好经过圆心O，
∴OD＝CD＝OC＝OA＝OB，
∴∠OAB＝∠OBA＝30°，
∴∠AOB＝180°﹣∠OAB﹣∠OBA＝120°，
∴∠APB＝AOB＝60°，
故选：D．
1．（2022秋•重庆期末）如图，AB是⊙O的直径，点C、D在⊙O上，若∠AOD＝130°，则∠C的度数是（ ）
A．35°B．30°C．25°D．20°
【答案】C
【解答】解：∵∠AOD＝130°，
∴∠BOD＝180°﹣∠AOD＝50°，
∴∠C＝BOD＝25°，
故选：C．
2．（2023•惠阳区校级开学）如图所示，四边形ABCD为⊙O的内接四边形，∠BCD＝120°，则∠BOD的大小是（ ）
A．60°B．110°C．120°D．90°
【答案】C
【解答】解：∵四边形ABCD为⊙O的内接四边形，
∴∠A＝180°﹣∠BCD＝60°，
由圆周角定理得，∠BOD＝2∠A＝120°，
故选：C．
3．（2022秋•西安期末）如图，AB、CD为⊙O的两条弦，⊙O的半径为r，AB＝r，CD＝r，连接AC、BD，AC与BD交于点H，则∠BHC的度数为（ ）
A．100°B．105°C．110°D．115°
【答案】B
【解答】解：如图，连接OA、OB、OC、OD、BC，
则OA＝OB＝OC＝OD＝r，
∵AB＝r，CD＝r，
∴△AOB是等边三角形，△OCD是等腰直角三角形，
∴∠AOB＝90°，∠COD＝90°，
∴∠ACB＝AOB＝30°，∠DBC＝∠COD＝45°，
∴∠BHC＝180°﹣∠ACB﹣∠DBC＝180°﹣30°﹣45°＝105°，
故选：B．
4．（2022秋•运城期末）如图所示，AB、CD是⊙O的两条互相垂直的弦，圆心角∠AOC＝140°，AD、CB的延长线相交于P，则∠P＝（ ）°．
A．40B．50C．60D．70
【答案】B
【解答】解：∵AB⊥CD，
∴∠BAD+∠CDA＝90°，
∵∠ABC＝∠ADC＝∠AOC＝70°，
∴∠BAD＝90°﹣70°＝20°，
∵∠ABC＝∠P+∠BAP，
∴∠P＝∠ABC﹣∠BAP＝70°﹣20°＝50°．
故选：B．
5．（2022秋•碑林区校级期末）如图，AB是半圆的直径，点C和D都在半圆上，已知∠ABC＝25°，那么∠CDB的度数为（ ）
A．140°B．115°C．110°D．120°
【答案】B
【解答】解：连接AC，
∵AB是直径，
∴∠ACB＝90°，
∵∠ABC＝25°，
∴∠CAB＝65°，
∵∠CAB+∠CDB＝180°，
∴∠CDB＝180°﹣65°＝115°．
故选：B．
6．（2022秋•南关区校级期末）如图，在边长为1的正方形网格中，点A，B，D在格点上，以AB为直径的圆过C，D两点，则cs∠BCD的值为（ ）
A．B．C．D．
【答案】D
【解答】解：∵AB是圆的直径，
∴∠ADB＝90°，
∴AB＝＝＝5，
∴cs∠BAD＝＝，
∵∠BCD＝∠BAD，
∴cs∠BCD＝cs∠BAD＝．
故选：D．
7．（2022秋•任城区校级期末）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝35°，则∠AOB的大小为（ ）
A．10°B．20°C．35°D．40°
【答案】B
【解答】解：∵∠BAC＝35°，
∴∠BOC＝2∠BAC＝2×35°＝70°，
∵∠AOC＝90°，
∴∠AOB＝∠AOC﹣∠BOC＝90°﹣70°＝20°，
故选：B．
8．（2022秋•江津区期末）如图，AB是⊙O的弦，半径OC⊥AB于点D，∠P＝26°，点P在圆周上，则∠A等于（ ）
A．26°B．30°C．34°D．38°
【答案】D
【解答】解：∵半径OC⊥AB于点D，
∴＝，
∴∠AOC＝2∠P＝52°，
∴△AOD是直角三角形，
∴∠A＝90°﹣∠AOC＝38°．
故选：D．
9．（2022秋•任城区校级期末）如图，点A，B，C在⊙O上，点D是AB延长线上一点，若∠AOC＝100°，则∠CBD的度数为（ ）
A．50°B．52.5°C．55°D．60°
【答案】A
【解答】解：设点E是优弧AC（不与A，C重合）上的一点，连接AE、CE，如图．
∵∠AOC＝100°，
∴∠E＝＝50°，
∵四边形ABCE内接于⊙O，
∴∠ABC＝180°﹣∠E＝130°，
∴∠CBD＝180°﹣∠ABC＝50°．
故选：A．
10．（2022秋•历下区期末）如图，AB为⊙O的直径，C，D为⊙O上的两点，若∠ACD＝56°，则∠DAB的度数为（ ）
A．34°B．36°C．46°D．54°
【答案】A
【解答】解：连接BC，如图
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠DAB＝∠DCB＝90°﹣∠ACD＝90°﹣56°＝34°．
故选：A．
11．（2022秋•郾城区校级期末）如图，⊙O的半径为3，将⊙O的一部分沿着弦AB翻折，劣弧恰好经过圆心O，则折痕AB的长为（ ）
A．1B．2C．D．
【答案】D
【解答】解：过O作OC⊥AB于D，交⊙O于C，连接OA，
Rt△OAD中，
OD＝CD＝OC＝，OA＝3，
根据勾股定理得，AD＝＝＝，
由垂径定理得，AB＝2AD＝3．
故选：D．
12．（2022秋•红桥区校级期末）如图，MN是⊙O的直径，A，B，C是⊙O上的三点，∠ACM＝60°，B点是的中点，P点是MN上一动点，若⊙O的半径为1，则PA+PB的最小值为（ ）
A．1B．C．D．﹣1
【答案】C
【解答】解：作点B关于MN的对称点B′，连接OA、OB、OB′、AB′，
则AB′与MN的交点即为PA+PB的最小时的点，PA+PB的最小值＝AB′，
∵∠ACM＝60°，
∴∠AOM＝2∠ACM＝2×60°＝120°，
∴∠AON＝60°，
∵点B为劣弧AN的中点，
∴∠BON＝∠AON＝×60°＝30°，
由对称性，∠B′ON＝∠BON＝30°，
∴∠AOB′＝∠AON+∠B′ON＝60°+30°＝90°，
∴△AOB′是等腰直角三角形，
∴AB′＝OA＝×1＝，
即PA+PB的最小值＝．
故选：C．
13．（2023•市南区一模）如图，四边形ABCD内接于⊙O，F是上一点，且＝，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC＝105°，∠BAC＝25°，则∠E的度数为（ ）
A．60°B．55°C．50°D．45°
【答案】C
【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝105°，
∴∠ADC＝180°﹣∠ABC＝180°﹣105°＝75°．
∵＝，∠BAC＝25°，
∴∠DCE＝∠BAC＝25°，
∴∠E＝∠ADC﹣∠DCE＝75°﹣25°＝50°．
故选：C．
14．（2022秋•桥西区校级期末）如图，四边形ABCD内接于⊙O，∠ABC＝135°，AC＝4．
（1）∠AOC的度数为 ；
（2）⊙O的半径为 ．
【答案】90°，．
【解答】解：（1）∵四边形ABCD内接于⊙O，∠ABC＝135°，
∴∠ADC＝180°﹣∠ABC＝45°，
∴∠AOC＝2∠ADC＝90°，
（2）在Rt△AOC中，设半径为r，
根据勾股定理可得，
2r2＝AC2＝16，
解得，
故答案为：90°，．
15．（2022秋•榆树市期末）如图，点A，B，C在⊙O上，若∠ABC＝130°，则∠AOC的度数是 ．
【答案】100°
【解答】解：如图，在优弧AC上取点D，连接AD，CD，
∵∠ABC＝130°，
∴∠ADC＝180°﹣∠ABC＝50°，
∴∠AOC＝2∠ADC＝100°．
故答案是：100°．
16.（2022•曲周县模拟）如图，AB是⊙O的直径，点C在⊙O上，CD平分∠ACB交⊙O于点D，若∠ABC＝30°，则∠CAD的度数为（ ）
A．100°B．105°C．110°D．120°
【答案】B
【解答】解：∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠BAC＝90°﹣∠ABC＝90°﹣30°＝60°，
∵CD平分∠ACB，
∴∠BCD＝45°，
∵∠BAD＝∠BCD＝45°，
∴∠CAD＝∠BAC+∠BAD＝60°+45°＝105°．
故选：B．