




专题12 二次函数图象性质与应用(共30道)-中考数学真题分项汇编(全国通用)
展开1.(2023·江苏徐州·统考中考真题)在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A.B.C.D.
【答案】B
【分析】根据二次函数图象的平移“左加右减,上加下减”可进行求解.
【详解】解:由二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为;
故选B.
【点睛】本题主要考查二次函数图象的平移,熟练掌握二次函数图象的平移是解题的关键.
2.(2023·辽宁沈阳·统考中考真题)二次函数图象的顶点所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】B
【详解】根据抛物线,可以写出该抛物线的顶点坐标,从而可以得到顶点在第几象限.
解:,
顶点坐标为,
顶点在第二象限.
故选:.
【点睛】本题主要考查了二次函数的性质,掌握二次函数的性质是解题的关键.
3.(2023·甘肃兰州·统考中考真题)已知二次函数,下列说法正确的是( )
A.对称轴为B.顶点坐标为
C.函数的最大值是-3D.函数的最小值是-3
【答案】C
【分析】根据二次函数的图象及性质进行判断即可.
【详解】二次函数的对称轴为,顶点坐标为
∵
∴二次函数图象开口向下,函数有最大值,为
∴A、B、D选项错误,C选项正确
故选:C
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数图象和性质是解题的关键.
4.(2023·贵州·统考中考真题)已知,二次数的图象如图所示,则点所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】D
【分析】首先根据二次函数的图象及性质判断a和b的符号,从而得出点所在象限.
【详解】解:由图可知二次函数的图象开口向上,对称轴在y轴右侧,
,,
,
在第四象限,
故选D.
【点睛】本题考查二次函数的图象与系数的关系,以及判断点所在象限,解题的关键是根据二次函数的图象判断出a和b的符号.
5.(2023·辽宁营口·统考中考真题)如图.抛物线与x轴交于点和点,与y轴交于点C.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y随x的增大而增大;⑤(m为任意实数)其中正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【分析】根据抛物线开口向下,与y轴交于正半轴,可得,根据和点可得抛物线的对称轴为直线,即可判断②;推出,即可判断①;根据函数图象即可判断③④;根据当时,抛物线有最大值,即可得到,即可判断⑤.
【详解】解:∵抛物线开口向下,与y轴交于正半轴,
∴,
∵抛物线与x轴交于点和点,
∴抛物线对称轴为直线,故②正确;
∴,
∴,
∴,故①错误;
由函数图象可知,当时,抛物线的函数图象在x轴上方,
∴当时,,故③正确;
∵抛物线对称轴为直线且开口向下,
∴当时,y随x的增大而减小,即当时,y随x的增大而减小,故④错误;
∵抛物线对称轴为直线且开口向下,
∴当时,抛物线有最大值,
∴,
∴,故⑤正确;
综上所述,正确的有②③⑤,
故选C.
【点睛】本题主要考查了抛物线的图象与系数的关系,抛物线的性质等等,熟练掌握抛物线的相关知识是解题的关键.
6.(2023·陕西·统考中考真题)在平面直角坐标系中,二次函数(为常数)的图像经过点,其对称轴在轴左侧,则该二次函数有( )
A.最大值B.最大值C.最小值D.最小值
【答案】D
【分析】将代入二次函数解析式,进而得出的值,再利用对称轴在轴左侧,得出,再利用二次函数的顶点式即可求出二次函数最值.
【详解】解:将代入二次函数解析式得:,解得:,,
∵二次函数,对称轴在轴左侧,即,
∴,
∴,
∴,
∴当时,二次函数有最小值,最小值为,
故选:.
【点睛】此题主要考查了二次函数的性质以及二次函数的最值,正确得出的值是解题关键.
7.(2023·湖北鄂州·统考中考真题)如图,已知抛物线的对称轴是直线,且过点,顶点在第一象限,其部分图象如图所示,给出以下结论:①;②;③;④若,(其中)是抛物线上的两点,且,则,其中正确的选项是( )
A.①②③B.①③④C.②③④D.①②④
【答案】D
【分析】根据二次函数的性质可得,,,可判断结论①;由处的函数值可判断结论②;由处函数值可判断结论③;根据得到点到对称轴的距离小于点到对称轴的距离可判断结论④.
【详解】解:二次函数开口向下,则,
二次函数对称轴为,则,,,
∴,故①正确;
∵过点,
∴由对称性可得二次函数与轴的另一交点为,
由函数图象可得时,
,故②正确;
时,
,
代入得:,故③错误;
∵对称轴是直线,
∴若,即时,,
∴当时,
点到对称轴的距离小于点到对称轴的距离
∵二次函数开口向下
∴,故④正确.
综上所述,正确的选项是①②④.
故选: D.
【点睛】本题考查了二次函数的综合,掌握二次函数的图象与各项系数符号的关系是解题关键.
8.(2023·山东日照·统考中考真题)在平面直角坐标系中,抛物线,满足,已知点,,在该抛物线上,则m,n,t的大小关系为( )
A.B.C.D.
【答案】C
【分析】利用解不等式组可得且,即可判断二次函数的对称轴位置,再利用函数的增减性判断即可解题.
【详解】解不等式组可得:,且
所以对称轴的取值范围在,
由对称轴位置可知到对称轴的距离最近的是,其次是,最远的是,
即根据增减性可得,
故选C.
【点睛】本题考查二次函数的图像和性质,求不等组的解集,掌握二次函数的图像和性质是解题的关键.
9.(2023·黑龙江牡丹江·统考中考真题)如图,抛物线经过点,.下列结论:①;②;③若抛物线上有点,,,则;④方程的解为,,其中正确的个数是( )
A.4B.3C.2D.1
【答案】D
【分析】根据二次函数图象可知:,,,得出,故①不正确;将点,代入,得出:,再求出,故②不正确;根据函数图象可得,故③正确;根据方程,,可知方程无解,故④不正确.
【详解】解:根据二次函数图象可知:,,,
∴,
∴,故①不正确;
将点,代入得出:,
得出:,
∴,
再代入得出:,故②不正确;
∵,
∴,,
∵,
∴,
根据图象可知:,故③正确;
∵方程,
∴,
∴方程无解,故④不正确;
正确的个数是1个,
故选:D.
【点睛】本题考查二次函数,掌握二次函数的性质是解题的关键.
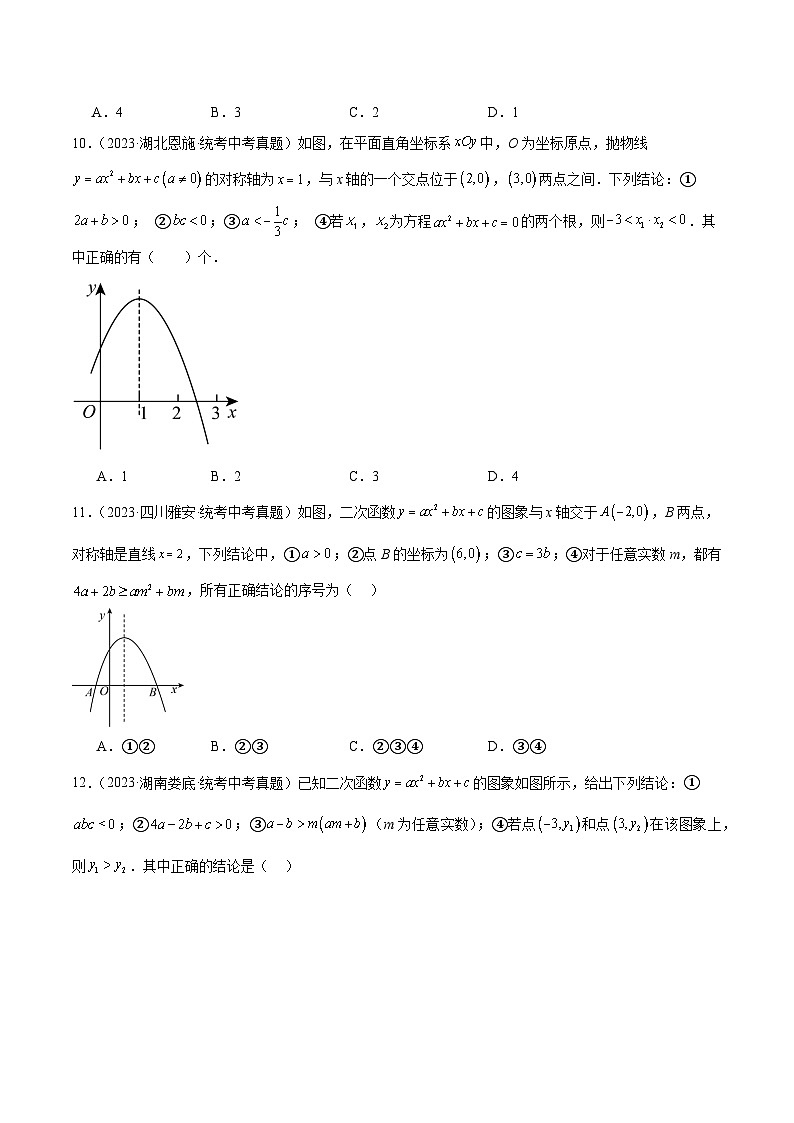
10.(2023·湖北恩施·统考中考真题)如图,在平面直角坐标系中,O为坐标原点,抛物线的对称轴为,与x轴的一个交点位于,两点之间.下列结论:①; ②;③; ④若,为方程的两个根,则.其中正确的有( )个.
A.1B.2C.3D.4
【答案】B
【分析】由图象得 ,,由对称轴得,,;抛物线与x轴的一个交点位于,两点之间,由对称性知另一个交点在,之间,得 ,于是,进一步推知,由根与系数关系知;
【详解】解:开口向下,得 ,与y轴交于正半轴,,
对称轴,,,故①错误;
故②错误;
抛物线与x轴的一个交点位于,两点之间,对称轴为,故知另一个交点在,之间,故时,
∴,得,故③正确;
由,,知,
∵,为方程的两个根,
∴
∴,故④正确;
故选:B
【点睛】本题考查二次函数图象性质,一元二次方程根与系数关系,不等式变形,掌握函数图象性质,注意利用特殊点是解题的关键.
11.(2023·四川雅安·统考中考真题)如图,二次函数的图象与x轴交于,B两点,对称轴是直线,下列结论中,①;②点B的坐标为;③;④对于任意实数m,都有,所有正确结论的序号为( )
A.①②B.②③C.②③④D.③④
【答案】C
【分析】根据抛物线开口方向可得a的符号,可对①进行判断;根据抛物线的对称轴,由二次函数的对称性可得B点坐标,由图象即可对②进行判断;根据点A,点B 代入解析式利用加减消元法可得,从而判定③,再由时函数取最大值判定④.
【详解】解:∵抛物线开☐向下,
∴,故①错误,
∵抛物线与y轴交于正半轴,
∴,
∴,
设点B坐标为
∵抛物线对称轴为直线,点A的坐标为,
∴,解得:,
∴点B的坐标为,故②正确,
∵点A的坐标为,点B的坐标为,
∴
∴由得,即,故③正确;
∵,抛物线对称轴为直线,
∴当时,时函数最大值,
当时,,
∴,即,
综上所述:正确的结论有②③④,
故选:C.
【点睛】本题主要考查二次函数图象与二次函数系数之间的关系,掌握数形结合思想的应用和二次函数图象与系数的关系,掌握二次函数的对称性是解题关键.
12.(2023·湖南娄底·统考中考真题)已知二次函数的图象如图所示,给出下列结论:①;②;③(m为任意实数);④若点和点在该图象上,则.其中正确的结论是( )
A.①②B.①④C.②③D.②④
【答案】D
【分析】由抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,可得,, ,故①不符合题意;当与时的函数值相等,可得,故②符合题意;当时函数值最大,可得,故③不符合题意;由点和点在该图象上,而,且离抛物线的对称轴越远的点的函数值越小,可得④符合题意.
【详解】解:∵抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,
∴,,,
∴,
∴,故①不符合题意;
∵对称轴为直线,
∴当与时的函数值相等,
∴,故②符合题意;
∵当时函数值最大,
∴,
∴;故③不符合题意;
∵点和点在该图象上,
而,且离抛物线的对称轴越远的点的函数值越小,
∴.故④符合题意;
故选:D.
【点睛】本题考查的是二次函数的图象与性质,熟记二次函数的开口方向,与y轴的交点坐标,对称轴方程,增减性的判定,函数的最值这些知识点是解本题的关键.
13.(2023·四川绵阳·统考中考真题)将二次函数的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
A.b>8B.b>﹣8C.b≥8D.b≥﹣8
【答案】D
【分析】先根据平移原则:上加下减,左加右减写出解析式,再列方程组,有公共点则△≥0,则可求出b的取值.
【详解】解:由题意得:平移后得到的二次函数的解析式为:,
则,
,
,
△=(﹣8)2﹣4×1×(8﹣b)≥0,
b≥﹣8,
故选:D.
【点睛】主要考查的是二次函数图象的平移和两函数的交点问题,二次函数与一次函数图象有公共点.
14.(2023·黑龙江大庆·统考中考真题)如图1,在平行四边形中,,已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点,同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
A.B.C.D.
【答案】C
【分析】根据题意可得:,,设,则,作交的延长线于点,作交的延长线于点,则可得,,从而得到,根据的最大值为3,求出的值,从而得到,最后由平行四边形的面积公式进行计算即可得到答案.
【详解】解:根据题意可得:,,
设,则,
作交的延长线于点,作交的延长线于点,
,
,
,
,,
,
由图象可得的最大值为3,
,
解得:或(舍去),
,
,
平行四边形的面积为:,
故选:C.
【点睛】本题主要考查了平行四边形的性质、解直角三角形、二次函数的图象与性质,熟练掌握平行四边形的性质、二次函数的图象与性质,添加适当的辅助线构造直角三角形,是解题的关键.
二、多选题
15.(2023·山东潍坊·统考中考真题)已知抛物线经过点,则下列结论正确的是( )
A.拋物线的开口向下
B.拋物线的对称轴是
C.拋物线与轴有两个交点
D.当时,关于的一元二次方程有实根
【答案】BC
【分析】将点代入可求出二次函数的解析式,再根据二次函数的图象与性质、二次函数与一元二次方程的联系逐项判断即可得.
【详解】解:将点代入得:,解得,
,
抛物线的开口向上,抛物线的对称轴是,选项A错误,选项B正确;
方程的根的判别式,
∴方程有两个不相等的实数根,
抛物线与轴有两个交点,选项C正确;
由二次函数的性质可知,这个抛物线的开口向上,且当时,取得最小值,
∴当时,与没有交点,
∴当时,关于的一元二次方程没有实根,选项D错误;
故选:BC.
【点睛】本题考查了二次函数的图象与性质、二次函数与一元二次方程的联系,熟练掌握二次函数的图象与性质是解题关键.
三、解答题
16.(2023·陕西·统考中考真题)某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为,还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:
方案一,抛物线型拱门的跨度,拱高.其中,点N在x轴上,,.
方案二,抛物线型拱门的跨度,拱高.其中,点在x轴上,,.
要在拱门中设置高为的矩形框架,其面积越大越好(框架的粗细忽略不计).方案一中,矩形框架的面积记为,点A、D在抛物线上,边在上;方案二中,矩形框架的面积记为,点,在抛物线上,边在上.现知,小华已正确求出方案二中,当时,,请你根据以上提供的相关信息,解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当时,求矩形框架的面积并比较,的大小.
【答案】(1)
(2),
【分析】(1)利用待定系数法则,求出抛物线的解析式即可;
(2)在中,令得:,求出或,得出,求出,然后比较大小即可.
【详解】(1)解:由题意知,方案一中抛物线的顶点,
设抛物线的函数表达式为,
把代入得:,
解得:,
∴;
∴方案一中抛物线的函数表达式为;
(2)解:在中,令得:,
解得或,
∴,
∴;
∵,
∴.
【点睛】本题主要考查了二次函数的应用,求二次函数解析式,解题的关键是熟练掌握待定系数法则,求出函数解析式.
17.(2023·甘肃兰州·统考中考真题)一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
【答案】(1)y关于x的函数表达式为
(2)运动员从起跳点到入水点的水平距离的长为
【分析】(1)由题意得抛物线的对称轴为,经过点,,利用待定系数法即可求解;
(2)令,解方程即可求解.
【详解】(1)解:由题意得抛物线的对称轴为,经过点,,
设抛物线的表达式为,
∴,解得,
∴y关于x的函数表达式为;
(2)解:令,则,
解得(负值舍去),
∴运动员从起跳点到入水点的水平距离的长为.
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键.
18.(2023·辽宁·统考中考真题)商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量(台)与销售单价(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
【答案】(1)
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
【分析】(1)用待定系数法求解即可;
(2)设销售利润为W元,列出W关于x的函数关系式,即可求得最大利润.
【详解】(1)解:由题意设,
由表知,当时,;当时,;
以上值代入函数解析式中得:,
解得:,
所以y与x之间的函数关系式为;
(2)解:设销售利润为W元,
则,
整理得:,
由于销售单价不低于进价,且不高于进价的2倍,则,
∵,,
∴当时,W随x的增大而增大,
∴当时,W有最大值,且最大值为2400;
答:当护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元.
19.(2023·江苏泰州·统考中考真题)阅读下面方框内的内容,并完成相应的任务.
任务:
(1)不等式的解集为_____________;
(2)3种方法都运用了___________的数学思想方法(从下面选项中选1个序号即可);
A.分类讨论 B.转化思想 C.特殊到一般 D.数形结合
(3)请你根据方法3的思路,画出函数图像的简图,并结合图像作出解答.
【答案】(1)
(2)D
(3)图像见解析,不等式的解集为
【分析】(1)如图1,作的图像,由方法1可知,不等式的解集为;
(2)由题意知,3种方法都运用了数形结合的数学思想方法;
(3)如图2,作函数与的图像,由图像可得,的解集为,或,进而可得的解集.
【详解】(1)解:如图1,作的图像,
由方法1可知,不等式的解集为,
故答案为:;
(2)解:由题意知,3种方法都运用了数形结合的数学思想方法,
故选:D;
(3)解:如图2,作函数与的图像,
由图像可得,的解集为,或,
综上,的解集为.
【点睛】本题考查了数形结合求一元二次不等式的解集,作二次函数、一次函数、反比例函数的图像.解题的关键在于理解题意并正确的作函数图象.
20.(2023·辽宁·统考中考真题)电商平台销售某款儿童组装玩具,进价为每件100元,在销售过程中发现,每周的销售量y(件)与每件玩具售价x(元)之间满足一次函数关系(其中,且x为整数).当每件玩具售价为120元时,每周的销量为80件;当每件玩具售价为140元时,每周的销量为40件.
(1)求y与x之间的函数关系式;
(2)当每件玩具售价为多少元时,电商平台每周销售这款玩具所获的利润最大?最大周利润是多少元?
【答案】(1)(其中,且x为整数)
(2)当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元
【分析】(1)设y与x之间的函数关系式为,利用待定系数法求解即可;
(2)设每周销售这款玩具所获的利润为W,列出W关于x的二次函数关系式,化为顶点式即可求解.
【详解】(1)解:设y与x之间的函数关系式为,
由已知得,
解得,
因此y与x之间的函数关系式为(其中,且x为整数);
(2)解:设每周销售这款玩具所获的利润为W,
由题意得,
,
W关于x的二次函数图象开口向上,
,且x为整数,
当时,W取最大值,最大值为1800,
即当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元.
【点睛】本题考查一次函数与二次函数的实际应用,列出周利润W关于x的二次函数关系式是解题的关键.
21.(2023·江苏宿迁·统考中考真题)某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.
(1)求两种商品的销售单价.
(2)经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?
【答案】(1)的销售单价为元、的销售单价为元
(2)当时,商场销售两种商品可获得总利润最大,最大利润是元
【分析】(1)设的销售单价为元、的销售单价为元,根据题中售出种20件,种10件,销售总额为840元;售出种10件,种15件,销售总额为660元列方程组求解即可得到答案;
(2)设利润为,根据题意,得到,结合二次函数性质及题中限制条件分析求解即可得到答案.
【详解】(1)解:设的销售单价为元、的销售单价为元,则
,解得,
答:的销售单价为元、的销售单价为元;
(2)解:种商品售价不低于种商品售价,
,解得,即,
设利润为,则
,
,
在时能取到最大值,最大值为,
当时,商场销售两种商品可获得总利润最大,最大利润是元.
【点睛】本题考查二元一次方程组及二次函数解实际应用题,读懂题意,根据等量关系列出方程组,根据函数关系找到函数关系式分析是解决问题的关键.
22.(2023·浙江·统考中考真题)根据以下素材,探究完成任务.
【答案】任务一:4m;任务二:;任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角
【分析】任务一:建立直角坐标系,由题意得:抛物线的顶点坐标为,设抛物线的解析式为,过点,利用待定系数法求出解析式,当时求出x的值即可得到;
任务二:建立直角坐标系,求出任务二的抛物线解析式,得到顶点纵坐标,与任务一的纵坐标相减即可;
任务三:根据题意给出合理的建议即可.
【详解】任务一:建立如图所示的直角坐标系,
由题意得:抛物线的顶点坐标为,
设抛物线的解析式为,过点,
∴,
解得,
∴,
当时,,
得(舍去),
∴素材1中的投掷距离为4m;
(2)建立直角坐标系,如图,
设素材2中抛物线的解析式为,
由题意得,过点,
∴,
解得,
∴
∴顶点纵坐标为,
(m),
∴素材2和素材1中球的最大高度的变化量为;
任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角.
【点睛】此题考查了二次函数的实际应用,求函数解析式,求抛物线与坐标轴的距离,正确理解题意建立恰当的直角坐标系是解题的关键.
23.(2023·山东潍坊·统考中考真题)为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余质量y(克)随时间x(分钟)变化的数据(),并分别绘制在直角坐标系中,如下图所示.
(1)从,,中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;
(2)查阅文献可知,该化学试剂发挥作用的最低质量为3克.在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?
【答案】(1)场景A中随变化的函数关系为,场景B中随变化的函数关系为
(2)场景B
【分析】(1)由图象可知,场景A中随变化的函数关系为,将,代入,进而可得;场景B中随变化的函数关系为,将代入,进而可得;
(2)场景A中当时,;场景B中,将代入,解得,,判断作答即可.
【详解】(1)解:由图象可知,场景A中随变化的函数关系为,
将,代入,得,
解得,
∴;
场景B中随变化的函数关系为,
将,代入,得,解得,
∴;
(2)解:场景A中当时,;
场景B中,将代入,得,解得,
∵,
∴该化学试剂在场景B下发挥作用的时间更长.
【点睛】本题考查了函数图象,一次函数解析式,二次函数解析式.解题的关键在于对知识的熟练掌握与灵活运用.
24.(2023·湖南益阳·统考中考真题)某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?
(3)2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
【答案】(1)4万元
(2)
(3)当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【分析】(1)把代入可得答案;
(2)当时,可得,再解方程可得答案;
(3)设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,,而,再利用二次函数的性质可得答案.
【详解】(1)解:∵投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,
当时,(万元);
(2)∵对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,
∴,
整理得:,
解得:,(不符合题意),
∴m的值为8.
(3)
设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,
∴
,
而,
∴当时,(万元);
∴当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【点睛】本题考查的是正比例函数的性质,一元二次方程的解法,列二次函数的解析式,二次函数的性质,理解题意,选择合适的方法解题是关键.
25.(2023·贵州·统考中考真题)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
【答案】(1)
(2)点的坐标为
(3)
【分析】(1)设抛物线的解析式为,将,代入即可求解;
(2)点B关于y轴的对称点,则,求出直线与y轴的交点坐标即可;
(3)分和两种情况,根据最小值大于等于9列不等式,即可求解.
【详解】(1)解:抛物线的对称轴与y轴重合,
设抛物线的解析式为,
,,
,,
将,代入,得:
,
解得,
抛物线的解析式为;
(2)解: 抛物线的解析式为,点到对称轴的距离是1,
当时,,
,
作点B关于y轴的对称点,
则,,
,
当,,A共线时,拉杆长度之和最短,
设直线的解析式为,
将,代入,得,
解得,
直线的解析式为,
当时,,
点的坐标为,位置如下图所示:
(3)解:中,
抛物线开口向下,
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
综上可知,或,
的取值范围为.
【点睛】本题考查二次函数的实际应用,涉及求二次函数解析式,求一次函数解析式,根据对称性求线段的最值,抛物线的增减性等知识点,解题的关键是熟练掌握二次函数的图象和性质,第3问注意分情况讨论.
四、填空题
26.(2023·黑龙江牡丹江·统考中考真题)将抛物线向下平移1个单位长度,再向右平移 个单位长度后,得到的新抛物线经过原点.
【答案】2或4/4或2
【分析】先求出抛物线向下平移1个单位长度后与的交点坐标,然后再求出新抛物线经过原点时平移的长度.
【详解】解:抛物线向下平移1个单位长度后的解析式为,
令,则,
解得,,
∴抛物线与的交点坐标为和,
∴将抛物线向右平移2个单位或4个单位后,新抛物线经过原点.
故答案为:2或4.
【点睛】此题考查了二次函数图象的平移与几何变换,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
27.(2023·山东泰安·统考中考真题)二次函数的最大值是 .
【答案】
【分析】利用配方法把二次函数一般式化为顶点式,即可求解.
【详解】解:利用配方法,将一般式化成顶点式:
二次函数开口向下,
顶点处取最大值,
即当时,最大值为.
故答案为:.
【点睛】本题考查二次函数的相关知识.将一般式化为顶点式,顶点处取到最值.其中配方法是解决问题的关键,也是易错点.
28.(2023·湖南娄底·统考中考真题)如图,抛物线与x轴相交于点、点,与y轴相交于点C,点D在抛物线上,当轴时, .
【答案】4
【分析】与抛物线与x轴相交于点、点,可得抛物线的对称轴为直线,由轴,可得,关于直线对称,可得,从而可得答案.
【详解】解:∵抛物线与x轴相交于点、点,
∴抛物线的对称轴为直线,
∵当时,,即,
∵轴,
∴,关于直线对称,
∴,
∴;
故答案为:4
【点睛】本题考查的是利用抛物线上两点的坐标求解对称轴方程,熟练的利用抛物线的对称性解题是关键.
29.(2023·吉林长春·统考中考真题)年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的地物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面 米.
【答案】
【分析】根据题意求出原来抛物线的解析式,从而求得平移后的抛物线解析式,再令求平移后的抛物线与轴的交点即可.
【详解】解:由题意可知:
、、,
设抛物线解析式为:,
将代入解析式,
解得:,
,
消防车同时后退米,即抛物线向左(右)平移米,
平移后的抛物线解析式为:,
令,解得:,
故答案为:.
【点睛】本题考查了待定系数法求抛物线解析式、函数图像的平移及坐标轴的交点;解题的关键是求得移动前后抛物线的解析式.
30.(2023·江苏泰州·统考中考真题)二次函数的图像与x轴有一个交点在y轴右侧,则n的值可以是 (填一个值即可).
【答案】(答案不唯一)
【分析】根据根与系数的关系即可求解.
【详解】解:设二次函数的图象与轴交点的横坐标为、,
即二元一次方程的根为、,
由根与系数的关系得:,,
一次函数的图象与轴有一个交点在轴右侧,
,为异号,
,
故答案为:(答案不唯一).
【点睛】本题考查抛物线与轴的交点,根与系数之间的关系,关键是根与系数之间的关系的应用.
销售单价(元)
…
50
60
70
…
月销量(台)
…
90
80
70
…
小丽学习了方程、不等式、函数后提出如下问题:如何求不等式的解集?
通过思考,小丽得到以下3种方法:
方法1 方程的两根为,,可得函数的图像与x轴的两个交点横坐标为、,画出函数图像,观察该图像在x轴下方的点,其横坐标的范围是不等式的解集.
方法2 不等式可变形为,问题转化为研究函数与的图像关系.画出函数图像,观察发现:两图像的交点横坐标也是、3;的图像在的图像下方的点,其横坐标的范围是该不等式的解集.
方法3 当时,不等式一定成立;当时,不等式变为;当时,不等式变为.问题转化为研究函数与的图像关系…
如何把实心球掷得更远?
素材1
小林在练习投掷实心球,其示意图如图,第一次练习时,球从点A处被抛出,其路线是抛物线.点A距离地面,当球到OA的水平距离为时,达到最大高度为.
素材2
根据体育老师建议,第二次练习时,小林在正前方处(如图)架起距离地面高为的横线.球从点A处被抛出,恰好越过横线,测得投掷距离.
问题解决
任务1
计算投掷距离
建立合适的直角坐标系,求素材1中的投掷距离.
任务2
探求高度变化
求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议
为了把球掷得更远,请给小林提出一条合理的训练建议.
专题12 二次函数图象性质与应用(共55题)-2023年中考数学真题分项汇编(全国通用): 这是一份专题12 二次函数图象性质与应用(共55题)-2023年中考数学真题分项汇编(全国通用),文件包含二次函数图象性质与应用共55题解析版pdf、二次函数图象性质与应用共55题学生版pdf等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
专题12 二次函数图象性质与应用(共30道)-2023年全国各地中考数学真题分项汇编(全国通用): 这是一份专题12 二次函数图象性质与应用(共30道)-2023年全国各地中考数学真题分项汇编(全国通用),文件包含专题12二次函数图象性质与应用共30道原卷版docx、专题12二次函数图象性质与应用共30道解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
专题12 二次函数图象性质与应用(55题)-2023年全国各地中考数学真题分项汇编(全国通用): 这是一份专题12 二次函数图象性质与应用(55题)-2023年全国各地中考数学真题分项汇编(全国通用),文件包含专题12二次函数图象性质与应用共55题原卷版docx、专题12二次函数图象性质与应用共55题解析版docx等2份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。













