北师大版（2021）拓展模块一 上册3.2.1 等差数列的概念和通项公式获奖课件ppt

这是一份北师大版（2021）拓展模块一 上册3.2.1 等差数列的概念和通项公式获奖课件ppt，文件包含北师大版《中职数学拓展模块一上册》第23课等差数列的概念与通项公式课件pptx、北师大版《中职数学拓展模块一上册》第23课等差数列的概念与通项公式教学设计docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。

泰姬陵坐落于印度古都阿格，是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建，她宏伟壮观，纯白大理石砌建而成的主体建筑叫人心醉神迷，成为世界七大奇迹之一。陵寝以宝石镶饰，图案之细致令人叫绝。 传说陵寝中有一个三角形图案，以相同大小的圆宝石镶饰而成，共有100层（见右图），奢靡之程度，可见一斑。你知道这个图案一共花了多少宝石吗？ 解析：这是一个等差数列的数学模型。
星期三的日期：1, 8, 15, 22, 29
同学们观察这个数列，有什么特点？
特点：从第2项起，每一项与它的前一项的差都等于常数1
特点：从第2项起，每一项与它的前一项的差都等于常数-3
观察如下几个数列，有什么共同点：
这个常数叫做等差数列的公差，通常用字母d 表示.
数列：2,5,6,7,…
数列：3,0,-3,-6，…
数列：5,5,5,5，…. d= 0每项都相等的数列叫做常数数列
例 1： 判断下列数列是否是等差数列：
注意：1、等差数列要求从第2项起，后一项与前一项作差。不能颠倒2、作差的结果要求是同一个常数
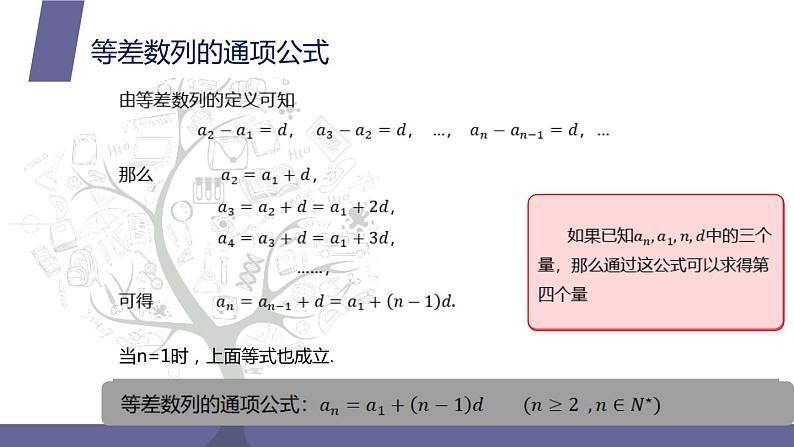
当n=1时，上面等式也成立.
例2 已知等差数列的首项是20 , 公差为-6, 请写出这个数列的2项和第4项。
例3 求等差数列-3, 1, 5, 9 .的第10 项.
例4 求等差数列-13, -17, -21, …, -361共有几项?
例5 一种车床变速箱的8个齿轮的齿数成等差数列，其中最大的和最小的两个齿轮 的齿数分别是24与45.求中间6个齿轮的齿数
【分析】在解一些实际问题时，要紧紧围绕等差数列的定义分析题意然后再寻找 解决问题的方法
要求适合某种条件且与已知角终边相同的角，其方法是先求出与已知角终边相同的角的一般形式，再依条件构建不等式求出k的值。
3、等差数列的概念解决实际问题：寻找等差数列的数学模型