中考数学一轮复习课件 第8章 统计与概率第35课统计（含答案）

这是一份中考数学一轮复习课件 第8章 统计与概率第35课统计（含答案），共14页。PPT课件主要包含了考点知识，全面调查，抽样调查，样本容量，中位数，例题与变式，过关训练等内容，欢迎下载使用。

1.考查全体对象的调查叫做__________，抽取一部分对象进行调查叫做__________．(选填“抽样调查”或“全面调查”)所要考察对象的全体叫做__________，总体的每一个考察对象叫做__________，抽取的部分个体叫做__________，样本中个体的数目叫做__________．(选填“总体”“样本”“样本容量”或“个体”)
2.平均数、众数、中位数是反映一组数据集中趋势的统计量．一组数据中出现次数最多的那个数据叫做这组数据的__________．如果这组数据按从小到大顺序排列，处于最中间位置的一个数据(或最中间两个数据的平均数) 叫做这组数据的__________．(选填“平均 数”“众数”“中位数”)
3.方差也是数据的代表，它们刻画了一组数据的__________程度或__________情况．一般地，对于n个数x1，x2，…，xn，把 叫做这n个数的__________，简记为s2.
4.频数表示每个对象出现的次数，频率表示每个对象出现的次数与总次数的比值(或百分比)．频数之和等于__________，频率之和等于__________.
5.统计的意义在于通过研究样本，去推断、估计__________，对现象作出解释，对未来进行预测.
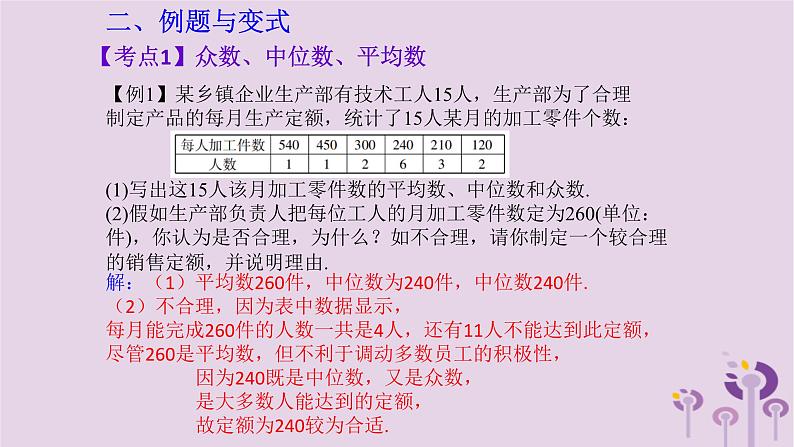
【例1】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：(1)写出这15人该月加工零件数的平均数、中位数和众数.(2)假如生产部负责人把每位工人的月加工零件数定为260(单位：件)，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由.
【考点1】众数、中位数、平均数
解：（1）平均数260件，中位数为240件，中位数240件.（2）不合理，因为表中数据显示，每月能完成260件的人数一共是4人，还有11人不能达到此定额，尽管260是平均数，但不利于调动多数员工的积极性， 因为240既是中位数，又是众数， 是大多数人能达到的定额， 故定额为240较为合适.
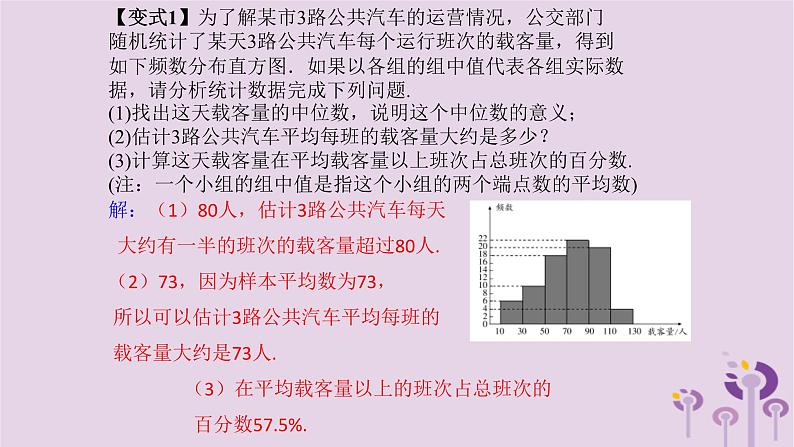
【变式1】为了解某市3路公共汽车的运营情况，公交部门随机统计了某天3路公共汽车每个运行班次的载客量，得到如下频数分布直方图．如果以各组的组中值代表各组实际数据，请分析统计数据完成下列问题.(1)找出这天载客量的中位数，说明这个中位数的意义；(2)估计3路公共汽车平均每班的载客量大约是多少？(3)计算这天载客量在平均载客量以上班次占总班次的百分数.(注：一个小组的组中值是指这个小组的两个端点数的平均数)
解：（1）80人，估计3路公共汽车每天 大约有一半的班次的载客量超过80人.（2）73，因为样本平均数为73， 所以可以估计3路公共汽车平均每班的 载客量大约是73人. （3）在平均载客量以上的班次占总班次的 百分数57.5%.
【考点2】众数、中位数、平均数、方差
【例2】某中学开展歌唱比赛活动，九年级(1)(2)班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示.(1)根据图示填写上表；(2)结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；(3)计算两班复赛成绩的方差，并说明哪个班级的成绩较稳定.
解：（1）九年级（1）班的平均数为85，中位数为85， 九年级（2）班的平均数为85，众数是100.（2）九年级（1）班成绩好些．因为两个班的平均数一样，平均水平一样，但九年级（1）班的中位数高，说明高分数比（2）班所以九年级（1）班成绩好些．（回答合理即可给分）（3）一班方差为70，二班方差为160, 所以九年级（1）班成绩稳定.
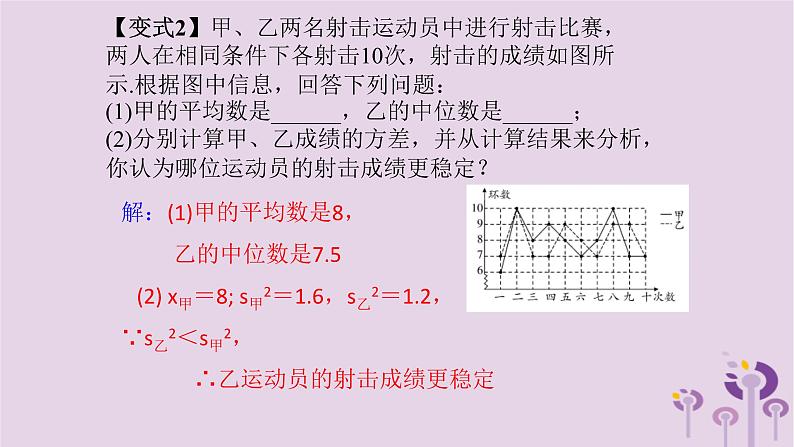
【变式2】甲、乙两名射击运动员中进行射击比赛，两人在相同条件下各射击10次，射击的成绩如图所示.根据图中信息，回答下列问题：(1)甲的平均数是______，乙的中位数是______；(2)分别计算甲、乙成绩的方差，并从计算结果来分析，你认为哪位运动员的射击成绩更稳定？
解：(1)甲的平均数是8， 乙的中位数是7.5 (2) x甲＝8; s甲2＝1.6，s乙2＝1.2，∵s乙2＜s甲2， ∴乙运动员的射击成绩更稳定
【考点3】频数、频率、统计思想
【例3】秋季新学期开学时，某中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：请根据上述统计图表，解答下列问题：(1)在表中， a＝______，b＝______，c＝______；(2)补全频数分布直方图；(3)根据以上选取的数据，计算七年级学生的平均成绩；(4)如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？
解：(1)a＝0.1，b＝0.3，c＝18.(2)补图略(3)平均成绩是81分(4)800×(0.3＋0.2）＝400，即“优秀”等次的学生约有400人.
【变式3】某校课外兴趣小组在本校学生中开展对“消防安全知识”了解情况的专题调查活动，采取随机抽样的方式进行问卷调查，调查的结果分为A，B，C，D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表格：(1)根据表中数据，问在关于调查结果的扇形统计图中，类别为B的学生数所对应的扇形圆心角的度数；(2)若A类学生数比D类学生数的2倍少4，求表中a，m的值；(3)若该校有学生955名，根据调查结果，估计该校学生中类别为C的人数约为多少？
解：（1）28÷0.35=80 ，32÷80×360°=144°, 类别B的学生数对应的扇形圆心角的度数为144°.（2）2a－4+32+28+a =80，a=8，m=12÷80=0.15.（3）955×0.35≈334，类别C的学生人数约是334.
1.下列调查中，适合采用全面调查方式的是(　　) A．对某学校某班50名同学体重情况的调查 B.对某河水质情况的调查 C.对某类烟花爆竹燃放安全情况的调查 D．对某市端午节期间市场上粽子质量情况的调查
3．16位参加百米半决赛同学的成绩各不相同，按成绩取前8位进入决赛．如果小刘知道了自己的成绩后，要判断能否进入决赛， 其他15位同学成绩的下列数据中，能使他得出结论 的是(　　) A．平均数　　　　　B．极差 C．中位数 D．方差
2.为了解某市八年级学生的肺活量，从中抽样调查了500名学生的肺活量，这项调查中的样本是(　　)A．某市八年级学生的肺活量 B.从中抽取的500名学生的肺活量C.从中抽取的500名学生 D．500
4．元旦欢会，班长对全班学生爱吃哪几种水果作了调查，为了确定买什么水果，最值得关注的应该是统计调查数据的__________．(填“中位数”“平均数”或“众数”)
5．一个容量为80的样本最大值为143，最小值为50，取组距为10，则可以分成__________组.
6．已知在一个样本中，50个数据分别落在5个组内，第一、二、三、五组数据的个数分别为2，8，15，5，则第四组的频率是__________.
7．一个扇形统计图中，扇形A，B，C，D的面积之比为 2∶3∶3∶4，则最大扇形的圆心角为________．
8．甲、乙两位同学参加数学综合素质测试，各项成绩如下(单位：分)：(1)分别计算甲、乙成绩的中位数；(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3∶3∶2∶2计算，那么甲、乙的数学综合素质成绩分别为多少分？
解：(1)甲成绩的中位数是90，乙成绩的中位数是93.(2)甲： (分)， 乙： (分)， 则甲的数学综合素质成绩为90.7分， 乙的数学综合素质成绩为91.8分.
9．某市为了准备中考体育测试，现在各学校九年级学生都在积极训练考试项目．某校学生小王对本班同学“自己选测的体育项目”进行了一次调查统计，下面是他用收集到的数据绘制的两幅不完整的统计图．根据图中提供的信息，解答下列问题：(1)该班共有________名学生；(2)补全条形统计图；(3)在扇形统计图中，“仰卧起坐”部分所对应的圆心角的度数等于________；(4)若小王所在学校共有600名毕业生，由此估计选测“掷实心球”的学生人数．
解：(1)该班共有50名学生. (2)图略. (3) 72° (4) (16÷50)×600＝ ×600＝192(人)