

2024北京石景山高三一模数学试题和答案
展开
这是一份2024北京石景山高三一模数学试题和答案,共13页。试卷主要包含了选择题等内容,欢迎下载使用。
第一部分(选择题 共 40 分)
一、选择题:共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
B
已知集合 A x x2 2x 3 0 , B x x 1,则 A
(1, 3)
(3,1)
(1,1)
(1, 3)
下列函数中,在区间(1,1) 上为减函数的是
f (x) sin x
f (x) cs x
f (x) ln(x 1)
f (x) 2x
一袋中有大小相同的 4 个红球和2 个白球. 若从中不放回地取球 2 次,每次任取1 个球,记“第一次取到红球”为事件 A ,“第二次取到红球”为事件 B ,则 P(B A)
A. 4
15
B. 2
5
C. 3
5
D. 4
5
设 , , 是三个不同平面,且 l , m ,则“ l // m ”是“ // ”的
充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
等差数列an 的首项为1 ,公差不为0 . 若 a2 , a3 , a6 成等比数列,则an 的前5 项和为
15
3
5D. 25
直线 y kx 1与圆 x2 ( y 1)2 16 相交于 A, B 两点,则线段 AB 的长度可能为
A. 5B. 7C. 9D.14
已知函数 f (x) 2sin( x ) ( 0,| | π) 的部分图象如图所示,则 f (π) 的值是
2
3
A.
B.1
C. 1
3
D.
设 a 20.3 , b sin π , c ln 2 ,则
12
c b a
b c a
a b c
b a c
中国民族五声调式音阶的各音依次为:宫、商、角、徵、羽,如果用这五个音,排成一个没有重复音的五音音列,且商、角不相邻,徵位于羽的左侧,则可排成的不同音列有
A.18 种B. 24 种C. 36 种D. 72 种
对于曲线C : x2 y2 1,给出下列三个命题:
①关于坐标原点对称;
②曲线C 上任意一点到坐标原点的距离不小于 2 ;
③曲线C 与曲线| x | | y | 3 有四个交点.其中正确的命题个数是
A. 0B.1C. 2D. 3
第二部分(非选择题 共 110 分)二、填空题共 5 小题,每小题 5 分,共 25 分。
复数 z 在复平面内对应的点为(1, 2) ,则 5 .
z
斜率为1 的直线l 经过抛物线 y2 4x 的焦点为 F ,且与该抛物线相交于 A, B 两点,则| AB | .
已知向量a, b 满足| b | 2 , a 与b 的夹角为 π ,则当实数 变化时, | b a | 的最小值为.
6
x3 3ax, x 1
设函数 f (x) .
3x a2 , x 1
①若 f (x) 有两个零点,则实数 a 的一个取值可以是;
②若 f (x) 是 R 上的增函数,则实数 a 的取值范围是.
黎曼函数在高等数学中有着广泛应用,其一种定义为: x [0,1] 时,
R(x) qqq
1 , x p ( p, q N*, p 为既约真分数)
0, x 0,1和(0,1)内的无理数
给出下列四个结论:
. 若数列an
R( n 1 , n N* ,
)
n
① an
1 ;
n
② an 2 an1 ;
n1
2
③ ai ai 1 ;
i 1
nn 1
2
④ ai ln.
i 1
其中所有正确结论的序号是.
三、解答题共 6 小题,共 85 分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题 13 分)
在锐角△ABC 中,角 A, B, C 的对边分别为 a, b, c ,且2b sin A 3a 0 .
求角 B 的大小;
求cs A cs C 的取值范围.
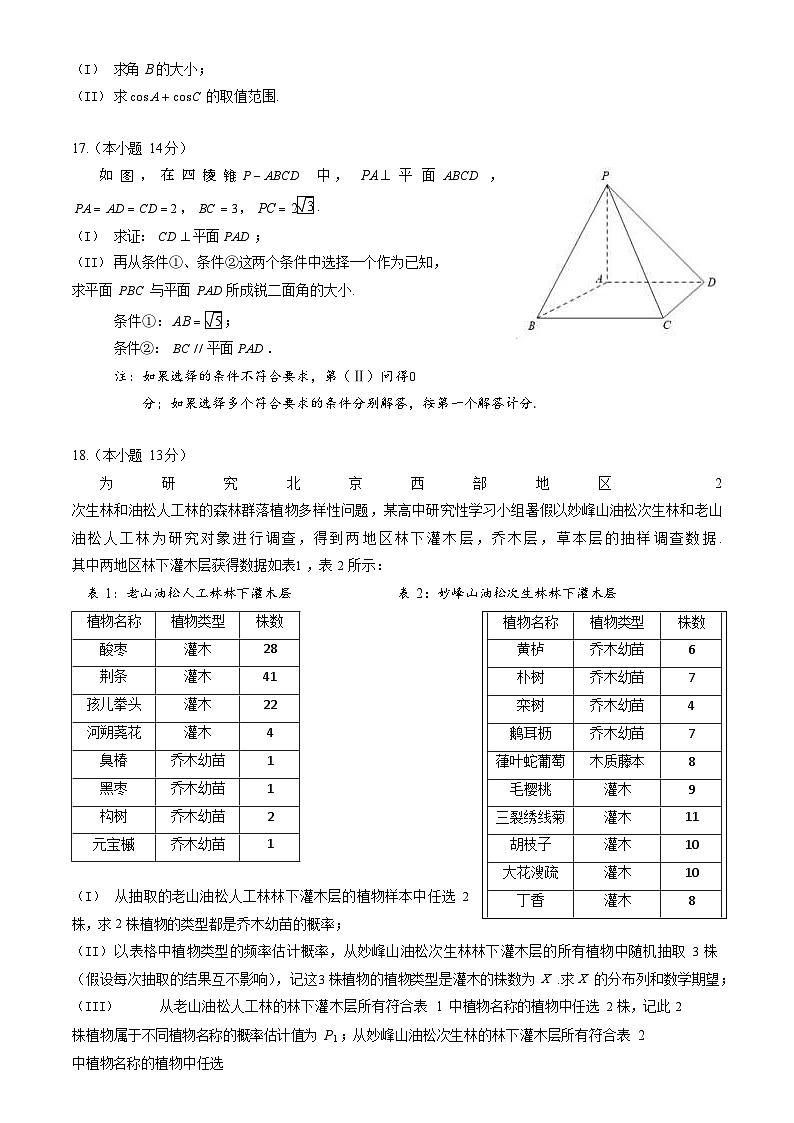
17.(本小题 14 分)
3
如 图 , 在 四 棱 锥 P ABCD PA AD CD 2 , BC 3 , PC 2
求证: CD 平面 PAD ;
中, PA 平 面 ABCD ,
.
再从条件①、条件②这两个条件中选择一个作为已知,求平面 PBC 与平面 PAD 所成锐二面角的大小.
5
条件①: AB ;
条件②: BC // 平面 PAD .
注:如果选择的条件不符合要求,第(Ⅱ)问得0 分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
18.(本小题 13 分)
为研究北京西部地区 2 次生林和油松人工林的森林群落植物多样性问题,某高中研究性学习小组暑假以妙峰山油松次生林和老山油松人工林为研究对象进行调查,得到两地区林下灌木层,乔木层,草本层的抽样调查数据. 其中两地区林下灌木层获得数据如表1 ,表 2 所示:
植物名称
植物类型
株数
黄栌
乔木幼苗
6
朴树
乔木幼苗
7
栾树
乔木幼苗
4
鹅耳枥
乔木幼苗
7
葎叶蛇葡萄
木质藤本
8
毛樱桃
灌木
9
三裂绣线菊
灌木
11
胡枝子
灌木
10
大花溲疏
灌木
10
丁香
灌木
8
表 1:老山油松人工林林下灌木层表 2:妙峰山油松次生林林下灌木层
从抽取的老山油松人工林林下灌木层的植物样本中任选 2
株,求 2 株植物的类型都是乔木幼苗的概率;
以表格中植物类型的频率估计概率,从妙峰山油松次生林林下灌木层的所有植物中随机抽取 3 株
(假设每次抽取的结果互不影响),记这3 株植物的植物类型是灌木的株数为 X .求 X 的分布列和数学期望;
从老山油松人工林的林下灌木层所有符合表 1 中植物名称的植物中任选 2 株,记此 2 株植物属于不同植物名称的概率估计值为 P1 ;从妙峰山油松次生林的林下灌木层所有符合表 2 中植物名称的植物中任选
植物名称
植物类型
株数
酸枣
灌木
28
荆条
灌木
41
孩儿拳头
灌木
22
河朔荛花
灌木
4
臭椿
乔木幼苗
1
黑枣
乔木幼苗
1
构树
乔木幼苗
2
元宝槭
乔木幼苗
1
2 株,记此 2 株植物属于不同植物名称的概率估计值为 P2 . 请直接写出 P1 与 P2 大小关系.(结论不要求证明)
19.(本小题 15 分)
已知函数 f (x) xeax (a 0) .
求曲线 y f (x) 在点(0, f (0)) 处的切线方程;
求 f (x) 在区间[1,1] 上的最大值与最小值;
当 a 1 时,求证: f (x) ln x x 1 .
20.(本小题 15 分)
x2
已知椭圆C : a2
y2
3
1 (a b 0) 的离心率为
b22
,短轴长为2.
2
求椭圆C 的方程;
设O 为坐标原点,过点 P(1, 3) 分别作直线l , l ,直线l 与椭圆相切于第三象限内
21 21
22
的点G ,直线l 交椭圆C 于 M , N 两点. 若| PG |2 | PM | | PN | ,判断直线l 与直线OG 的位置关系,并说明理由.
21.(本小题 15 分)
n
已知集合 Sn X X (x1 , x2 ,, xn ) , xi 0,1,i 1, 2, , n (n 2) ,对于 A (a1 , a2 ,, an ) ,
B (b1 , b2 ,,bn ) Sn ,定义 A 与 B 之间的距离为 d ( A, B) | ai bi | .
i 1
(Ⅰ)已知 A (1,1,1, 0) S4 ,写出所有的 B S4 ,使得 d ( A, B) 1 ;
已知 I (1,1,,1) Sn ,若 A, B Sn ,并且 d (I , A) d (I , B) p n ,求 d ( A, B) 的最大值;
设集合 P Sn , P 中有 m (m 2) 个元素,若 P 中任意两个元素间的距离的最小值为 t ,求证:
m 2ni 1 .
石景山区 2024 年高三统一练习
数学参考答案
一、选择题(共 10 小题,每小题 4 分,共 40 分)
二、填空题(共 5 小题,每小题 5 分,共 25 分)
( 1 ) D
( 2 ) D
( 3 ) C
( 4 ) B
( 5 ) A
( 6 ) B
( 7 ) A
( 8 ) B
( 9 ) C
(10)C
(11) 1 2i
(12) 8
[2, )
(13) 1(14) 1 [0,1]
(15)②③④
三、解答题(共 6 小题,共 85 分)
(16)(本小题 13 分)
解:(Ⅰ)在锐角△ ABC 中,根据正弦定理
b
sin B
a,有
sin A
2sin B sin A 3 sin A 0 ,
因为 A
B
π
(0, )
2
π
,所以sin A 0 ,所以sin B ,
3
2
因为(0, ) ,即 B 【6 分】
23
(Ⅱ)由(Ⅰ)知 A C 2π .
3
cs A cs C cs( B C) cs C
cs( 2 C) cs C
3
1 cs C 3 sin C cs C
22
1 cs C 3 sin C
22
sin(C )
6
在锐角△ ABC 中,因为 C ,所以 C 2
62
所以sin(C ) ( 3 ,1]
363
【13 分】
62
(17)(本小题 14 分)
解:(Ⅰ)因为 PA 平面 ABCD , AD,CD 平面 ABCD ,所以 PA AD, PA CD
z
P
A
Dy
E
C
x
在 Rt△PAD 中, PA AD 2 ,
2
所以 PD 2.
3
因为 PD 2 2,CD 2, PC 2
所以 PD2 CD2 PC2 ,即CD PD
PA P
又因为 PDB
所以CD 平面 PAD .【6 分】
(Ⅱ)选条件①
在平面 ABCD 上过 A 点作 AE // CD 交 BC 于 E 点,
根据(Ⅰ)知 PA AD, PA AE, AD AE ,建立以 A 为原点,
向量 AE , AD, AP 方向为 x 轴, y 轴, z 轴正方向的空间直角坐标系.
2
5
连接 AC ,易知 AC 2,因为 AB , BC 3 ,
2
AC2 BC 2 AB28 9 5
2 2 2 3
在△ ABC 中, csACB
2 AC BC2
所以ACB ,因为ACD ,所以 BC CD ,
44
易证四边形 AECD 为正方形.
A(0, 0, 0) , P(0, 0, 2) , B(2, 1, 0) , C(2, 2, 0) , D(0, 2, 0)
PB (2, 1, 2) , PC (2, 2, 2)
设平面 PBC 的法向量为n (x, y, z) ,则
n PB 0 即 2x y 2z 0
2x 2 y 2z 0
n PC 0
解得 y 0, x z ,令 x z 1 ,则n (1, 0,1) ,
由(Ⅰ)知平面 PAD 的法向量为 CD (2, 0, 0) ,
cs CD, n
2 .
CD n
| CD || n |
2 2
2
2
所以,平面 PBC 与平面 PAD 所成锐二面角的大小为 .【14 分】
4
选条件②
因为 BC // 平面 PAD ,平面 ABCD 平面 PAD AD , BC 平面 ABCD
所以 BC // AD .
在平面 ABCD 上过 A 点作 AE // CD 交 BC 于 E 点,易证四边形 AECD 为正方形,
根据(Ⅰ)知 PA AD, PA AE, AD AE ,建立以 A 为原点,
向量 AE , AD, AP 方向为 x 轴, y 轴, z 轴正方向的空间直角坐标系.
则 A(0, 0, 0) , P(0, 0, 2) , B(2, 1, 0) , C(2, 2, 0) , D(0, 2, 0)
PB (2, 1, 2) , PC (2, 2, 2)
设平面 PBC 的法向量为n (x, y, z) ,则
n PB 0 即 2x y 2z 0
2x 2 y 2z 0
n PC 0
解得 y 0, x z ,令 x z 1 ,则n (1, 0,1) ,
由(Ⅰ)知平面 PAD 的法向量为 CD (2, 0, 0) ,
cs CD, n
2
.
2
2
CD n
| CD || n |
2 2
所以,平面 PBC 与平面 PAD 所成锐二面角的大小为 .【14 分】
4
(18)(本小题 13 分)
解:(Ⅰ)设事件 A 为“从抽取的老山油松人工林林下灌木层的植物样本中任选2 株,
2 株植物的类型都是乔木幼苗”,由表格知,样本中老山油松人工林林下灌
C21
木层的植物共有100 株,其中乔木幼苗有5 株,所以 P( A) 估计为 5 .
C
2
100
495
【3 分】
由题意可知,从抽取的妙峰山油松次生林灌木层的植物样本中随机抽取1
株植物是灌木的概率估计为 48 3 , X 的可能取值是0,1, 2,3 .
805
所以 P( X 0) 估计为(1 3)3 8
; P( X 1) 估计为C1 3 2 2
36 ;
5125
3( )
55
125
( )
P( X 2) 估计为C2 3 2 2 54 ; P( X 3) 估计为
3 3 27 .
355125
( )
5125
随机变量 X 的分布列为
所以 EX 估计为0 8 1 36 2 54 3 27 9 .
1251251251255
X339
X
0
1
2
3
P
8
125
36
125
54
125
27
125
或因为
B(3, ) ,所以 EX 估计为3 【10 分】
555
P2 P1 .【13 分】
(19)(本小题 15 分)
解:(Ⅰ) f (x) eax ax eax (ax 1)eax ,
所以 f (0) (0 1)e0 1 , f (0) 0 .
所以 f (x) 在(0, f (0)) 点处的切线方程为 y x .【4 分】
(Ⅱ)因为 f (x) (ax 1)eax ,令 f (x) 0 ,由已知a 0 ,解得 x 1 .
a
当 x 变化时, f (x) ,f (x) 随 x 的变化如下表:
所以①当 1 ≤ 1 ,即0 a ≤1 时, f (x) 在[1,1] 为增函数,
a
则 f (x)min f (1) ea , f (x)max f (1) ea .
②当1 1 1,即a 1时,
a
f (x) 在[1, 1 ] 为减函数,在[ 1 ,1] 为增函数.
aa
x
(, 1 )
a
1
a
( 1 ,+)
a
f (x)
0
+
f (x)
减函数
极小值
增函数
则 f (x)
min
f ( 1 ) 1 e1 ,而 f (1) ea 0 , f (1) ea 0 ,
aa
所以 f (1) f (1) ,即 f (x)max f (1) ea .
(Ⅲ)当a 1时, f (x) xex ,
令 F (x) f (x) (ln x x 1) xex lnx x 1
则 F (x) (x 1)ex 1 1 x 1 (xex 1) ,
xx
(x 0) ,
【10 分】
令G(x) xex 1,则当 x 0 时, G(x) (x 1)ex 0 ,所以函数G( x) 在区间(0, ) 上是增函数,
又G(0) 1 0 , G(1) e 1 0 ,
所以函数G( x) 存在唯一的零点 x0 (0, ) ,
且当 x (0, x0 ) 时, G(x) 0 ;当 x (x0 , ) 时, G(x) 0 .
所以当 x (0, x0 ) 时, F (x) 0 ;当 x (x0 , ) 时, F (x) 0 .所以函数 F ( x) 在(0, x0 ) 上为减函数,在(x0 , ) 上为增函数,故 F (x)min F (x0 ) x0ex0 lnx0 x0 1,
由G(x ) 0 得 x0ex0 1 0 ,即 x ex0 1 .
00
两边取对数得lnx0 x0 0 ,故 F (x0 ) 0 ,
所以 F ( x) ≥ 0 恒成立,即 f (x) ≥ ln x x 1.【15 分】
2
2
(20)(本小题 15 分)
a
c 3 ,
解:(Ⅰ)由题意得2
解得a 2
, b .
2b 2 2,
a2 b2 c2 ,
x2y2
所以椭圆C 的方程为
82
1 .【5 分】
直线l2 与直线OG 平行.证明如下:
显然直线l 斜率存在,设直线l 方程为 y 3 m(x 1) .
112
x2 4 y2 8,
由
y m(x 1) 3
得(4m2 1)x2 (8m2 12m)x 4m2 12m 1 0 .
2
因为直线l1 与椭圆相切,
(8m2 12m)2 4(4m2 1) (4m2 12m 1) 4(28m2 12m 1) ,
令 0 解得m 1 或m 1 .
214
因为直线l1 与椭圆相切于第三象限内的点G ,所以m
所以m 1 ,所以2x2 8x 8 0 , x 2 ,
舍去.
14
所以 y
2
1 (x
G
1) 3 1 ,
G2G2
所以G(2, 1) ,直线OG 斜率为 1 , | PG |2 5
24
直线l 的斜率不存在时, | PM || PN | 1 ,
22
所以| PG |2 | PM | | PN |,不成立.
设直线l 的方程为 y 3 k (x 1) , M (x , y ) , N (x , y ) ,
22
x2 4 y2 8,
1122
由
y k(x 1) 3
,得(4k 2 1)x2 (8k 2 12k)x 4k 2 12k 1 0 .
2
2
直线l 交椭圆C 于 M , N 两点. 4(28k 2 12k 1) 0 ,
所以k 1 或 k 1 .
214
所以 x1 x2
12k 8k 2
(x 1) ( y )
2
3
2
1
1
2
1 4k 2
, x1 x2
4k 2 12k 1
.
1 k 2
1 k 2
1 4k 2
| PM |
| x1
1| ,同理| PN |
| x2
1|
所以| PM | | PN |(1 k 2 ) x1
1 x2
1 (1 k 2 ) | x1x2 (x1 x2 ) 1|
(1 k 2 )
2.
4k 2 1
所以(1 k 2 )2 5 ,解得k 1 或k 1 ;
4k 2 1422
因为k 1 或 k 1
214
,所以k 1 .
2
所以直线l2 与直线OG 平行.【15 分】
(21)(本小题 15 分)
解:(Ⅰ)(1,1,1,1),(1,1, 0, 0),(1, 0,1,0),(0,1,1,0).【4 分】
nn
(Ⅱ) d (I , A) | ai 1| |1 ai |
i1i1
1 an
an )
1 a1 1 a2 n (a1 a2 p
所以a1 a2 an n p .
同理b1 b2 bn n p .
①当n p p ,即n 2 p 时
nnn
d ( A, B) | ai bi |≤ | ai | | bi | n p n p 2n 2 p .
i1
i1
i1
例如当 A (1,1,1,,1, 0,0, ,0), B (0, 0, 0,, 0,1,1, ,1)时,等号成立.
pn p
n pp
②当n p ≥ p ,即n ≥ 2 p 时
nnnn
d ( A, B) | ai bi | | ai 1 1 bi |≤ | ai 1| |1 bi | p p 2 p .
i1
i1
i1
i1
同理可知等号成立.
2 p ,
p ≤ n
所以d ( A, B)
max
2n 2 p ,
.【10 分】
p n
2
记 P {(c1, c2 ,, cnt 1)| (c1, c2 ,, cnt 1,, cn ) P},
①显然集合 P 中元素的个数小于等于集合 P 中元素的个数;
② A, B Sn 且 A B ,假设它们满足a1 b1, a2 b2 ,, ant 1 bnt 1 ,则由定义必有d ( A, B) ≤ t 1,与 P 中不同元素间距离至少为t 相矛盾.从而(a1, a2 ,, ant 1 ) (b1,b2 ,,bnt 1) .
从而集合 P 中元素的个数等于集合 P 中元素的个数,即均为m 个.又因为 P 中元素有n t 1 个分量,
所以集合 P 至多有2nt1 个元素,从而m ≤ 2nt1 成立.【15 分】
(以上解答题,若用其它方法,请酌情给分)
相关试卷
这是一份2024北京延庆高三一模数学试题及答案,共11页。
这是一份2023年北京市石景山区高三一模考试数学试卷(含答案解析),共12页。试卷主要包含了 已知数列{an}满足, 已知直线l等内容,欢迎下载使用。
这是一份北京市石景山区2023届高三一模数学试题 (原卷版),共8页。试卷主要包含了单选题,填空题,解答题,双空题等内容,欢迎下载使用。








