第7章 平面向量、复数 第3节 平面向量的数量积 2025届高考数学一轮总复习(适用于新高考新教材)ppt

这是一份第7章 平面向量、复数 第3节 平面向量的数量积 2025届高考数学一轮总复习(适用于新高考新教材)ppt，共45页。PPT课件主要包含了目录索引，a⊥b，ACD等内容，欢迎下载使用。

研考点 精准突破
强基础 固本增分
　其中夹角为0时两向量同向共线,夹角为π时两向量反向共线
(2)向量的数量积已知两个非零向量a与b,它们的夹角为θ,我们把数量__________叫做向量a与b的数量积(或内积),记作a·b,即a·b=|a||b|cs θ. 
数量积是一个实数,可正可负可0
规定:零向量与任一向量的数量积为__________. 
微思考两个向量的数量积大于0(或小于0),则夹角一定为锐角(或钝角)吗?
提示 不一定.当两个向量的夹角为0(或π)时,数量积也大于0(或小于0).
2.平面向量数量积的性质及坐标表示已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
不要与向量平行的坐标公式混淆
3.向量数量积的运算律
微点拨向量的数量积运算不满足结合律和消去律,即:(1)(a·b)c不一定等于a(b·c);(2)a·b=a·c(a≠0)不能推出b=c.
常用结论1.平面向量数量积运算的常用公式:(1)(a+b)·(a-b)=a2-b2;(2)(a±b)2=a2±2a·b+b2.2.有关向量夹角的两个结论(1)两个向量a与b的夹角为锐角,则有a·b>0,反之不成立(因为a与b夹角为0时不成立).(2)两个向量a与b的夹角为钝角,则有a·b<0,反之不成立(因为a与b夹角为π时不成立).
5.(人教A版必修第二册习题6.2第11(2)题改编)已知|a|=2,|b|=5,且a·b=-3,则|a+b|=__________. 
6.(人教A版必修第二册6.2.4节例13改编)已知|a|=3,|b|=4,且a与b不共线,若向量a+kb与a-kb互相垂直,则实数k=__________. 
题组三 连线高考7.(2022·全国乙,文3)已知向量a=(2,1),b=(-2,4),则|a-b|=(　　)A.2B.3C.4D.5
8.(2023·全国甲,文3)已知向量a=(3,1),b=(2,2),则cs=(　　)
9.(2022·全国甲,文13)已知向量a=(m,3),b=(1,m+1).若a⊥b,则m=_________.
考点一 平面向量数量积的运算
[对点训练1](1)(2024·山东潍坊模拟)已知平面向量a与b的夹角是60°,且|a|=2,b=(1,2),则a·(2a-b)=(　　)
考点二 平面向量数量积的应用(多考向探究预测)
考向1 向量的模例2(1)(2024·湖南长郡中学模拟)已知a=(1,2),b=(2,t),若|a+b|=|a-b|,则t的值为__________. 
考向2 向量的夹角例3(1)(2020·全国Ⅲ,理6)已知向量a,b满足|a|=5,|b|=6,a·b=-6,则cs=(　　)
解析 ∵a·(a+b)=a2+a·b=25-6=19,|a+b|2=a2+b2+2a·b=25+36-12=49,∴|a+b|=7,
(2)已知非零向量a=(x,3x),b=(-2x,1),若a与b的夹角为钝角,则x的取值范围是(　　)
变式探究(变条件)在本例(2)中,其他条件不变,若向量a与b的夹角为锐角,则x的取值范围是__________. 
考向3 向量的垂直例4(1)(2023·新高考Ⅰ,3)已知向量a=(1,1),b=(1,-1).若(a+λb)⊥(a+μb),则(　　)A.λ+μ=1B.λ+μ=-1C.λμ=1D.λμ=-1
解析 (方法1)由题意得,a+λb=(1+λ,1-λ),a+μb=(1+μ,1-μ).∵(a+λb)⊥(a+μb),∴(1+λ)(1+μ)+(1-λ)(1-μ)=0,解得λμ=-1.故选D.(方法2)由题意得,a2=12+12=2,b2=12+(-1)2=2,a·b=1×1+1×(-1)=0.∵(a+λb)⊥(a+μb),∴(a+λb)·(a+μb)=a2+(λ+μ)a·b+λμb2=2+0+2λμ=0.解得λμ=-1.故选D.
(2)(2020·全国Ⅱ,文5)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是(　　)A.a+2bB.2a+bC.a-2bD.2a-b
规律方法平面向量垂直问题的两个类型
(2)(2024·广东广州模拟)已知两个非零向量a,b满足|a|=3|b|,(a+b)⊥b,则cs=(　　)
解析 因为(a+b)⊥b,所以(a+b)·b=0,所以a·b+b2=0,所以a·b=-|b|2,
(4)(2020·全国Ⅱ,理13)已知单位向量a,b的夹角为45°,ka-b与a垂直,则k=__________. 
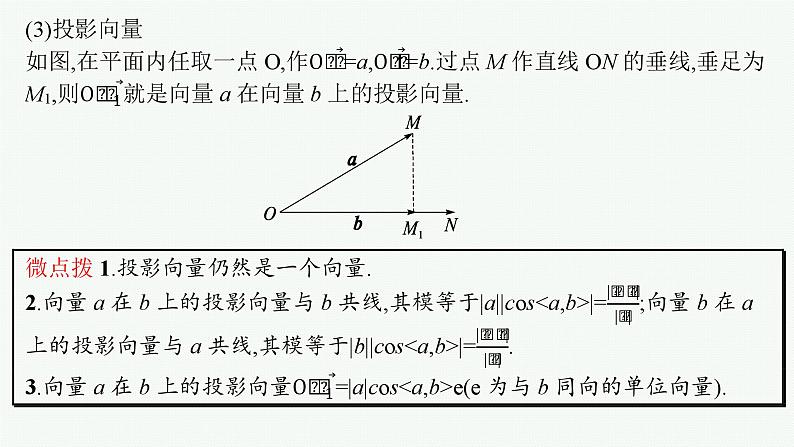
考点三 投影向量及其应用
解析 a⊥(a+b),则a·(a+b)=a2+a·b=9+a·b=0,故a·b=-9,
[对点训练3](2024·山东淄博模拟)已知向量a,b满足a·b=10,且b=(6,-8),则a在b上的投影向量为(　　)
考点四 平面向量的实际应用
例6(多选题)在日常生活中,我们常常会看到两个人共提一个行李包的情景,若行李包所受的重力为G,两个拉力分别为F1,F2,且|F1|=|F2|,F1与F2夹角为θ, θ∈(0,π),当两人拎起行李包时,下列结论错误的有(　　)
[对点训练4]如图,一个力F作用于小车G,使小车G发生了40米的位移,F的大小为50 N,且与小车的位移方向的夹角为60°,e是与小车位移方向相同的单位向量,则F在e上的投影向量为__________.
解析 因为|F|=50 N,且F与小车的位移方向的夹角为60°,所以F在e上的投影向量为|F|cs 60°e=25e.