2024年新高考数学题型全归纳讲义第二十讲立体几何大题综合归类(原卷版+解析)

这是一份2024年新高考数学题型全归纳讲义第二十讲立体几何大题综合归类(原卷版+解析)，共77页。
TOC \ "1-1" \h \u \l "_Tc31183" 题型01平行：无交线型 PAGEREF _Tc31183 \h 1
\l "_Tc15411" 题型02平行：线面平行探索性3
\l "_Tc19920" 题型03平行：面面平行探索性 PAGEREF _Tc19920 \h 4
\l "_Tc30670" 题型04 垂直：线面垂直探索性 PAGEREF _Tc30670 \h 5
\l "_Tc25026" 题型05垂直：面面垂直翻折探索性7
\l "_Tc7885" 题型06证明与建系：斜棱柱垂面法建系8
\l "_Tc7905" 题型07证明与建系：斜棱柱垂线法建系10
\l "_Tc16696" 题型08 证明与建系：三棱柱投影法建系12
\l "_Tc23017" 题型09 证明与建系：角平分线法建系 PAGEREF _Tc23017 \h 13
\l "_Tc6755" 题型10二面角延长线法 PAGEREF _Tc6755 \h 15
\l "_Tc23619" 题型11翻折型 PAGEREF _Tc23619 \h 16
\l "_Tc25583" 题型12台体型 PAGEREF _Tc25583 \h 18
\l "_Tc8054" 高考练场19
热点题型归纳
题型01平行：无交线型
【解题攻略】
【典例1-1】如图，在平行四边形中，，，为的中点，以为折痕将折起，使点到达点的位置，且，，分别为，的中点.
(1)证明：平面.
(2)若平面与平面的交线为，求直线与平面所成角的正弦值.
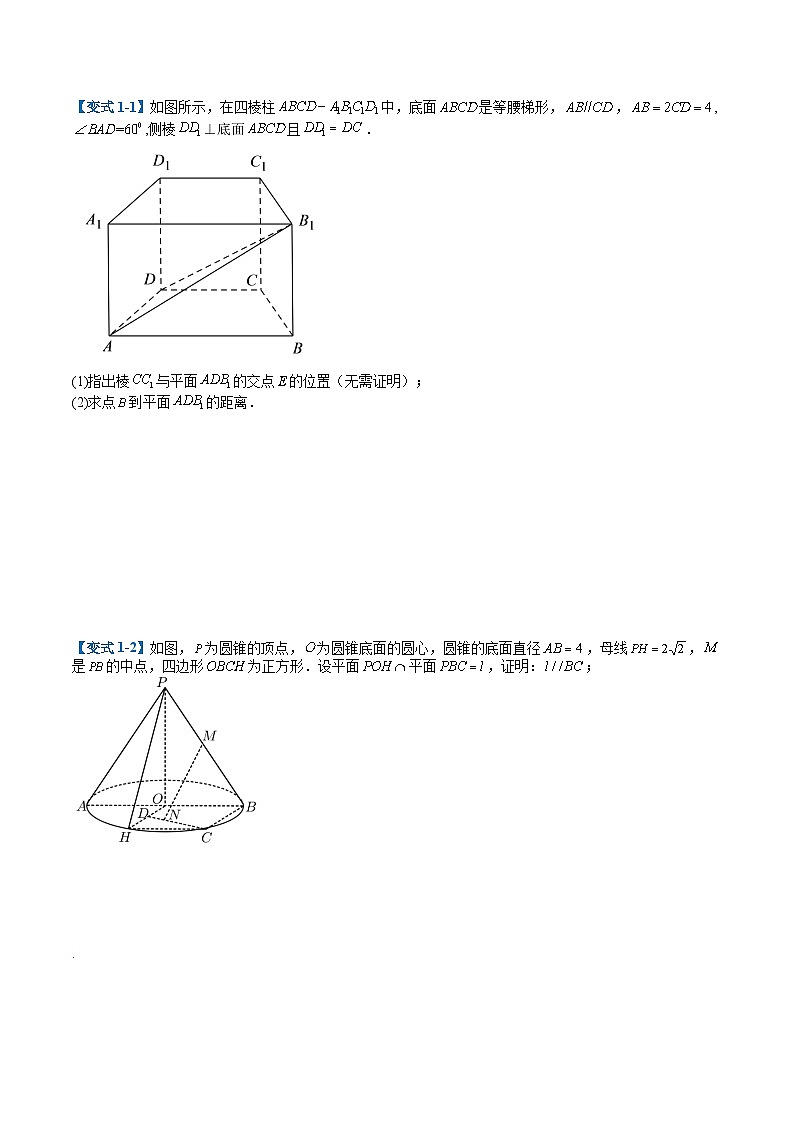
【变式1-1】如图所示，在四棱柱中，底面是等腰梯形，，,,侧棱⊥底面且．
(1)指出棱与平面的交点的位置（无需证明）；
(2)求点到平面的距离．
【变式1-2】如图，为圆锥的顶点，为圆锥底面的圆心，圆锥的底面直径，母线，是的中点，四边形为正方形．设平面平面，证明：；
.
题型02平行：线面平行探索性
【解题攻略】
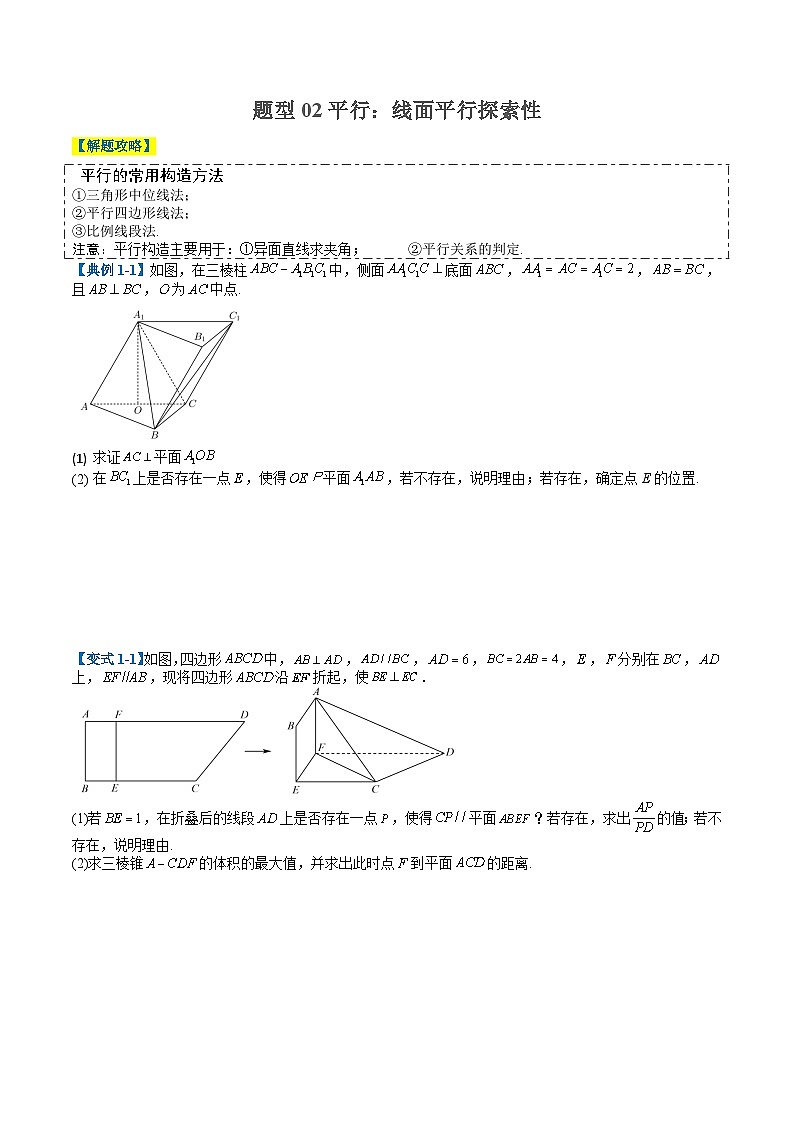
【典例1-1】如图，在三棱柱中，侧面底面，，，且，为中点.
求证平面
在上是否存在一点，使得平面，若不存在，说明理由；若存在，确定点E的位置.
【变式1-1】如图，四边形中，，，，，，分别在，上，，现将四边形沿折起，使．
(1)若，在折叠后的线段上是否存在一点，使得平面？若存在，求出的值；若不存在，说明理由.
(2)求三棱锥的体积的最大值，并求出此时点到平面的距离.
【变式1-2】如图，在直角梯形ABCD中，AB∥DC，∠BAD＝90°，AB＝4，AD＝2，DC＝3，点E在CD上，且DE＝2，将△ADE沿AE折起，使得平面ADE⊥平面ABCE，G为AE中点.
(1)求证：DG⊥平面ABCE；
(2)求四棱锥D-ABCE的体积；
(3)在线段BD上是否存在点P，使得CP∥平面ADE？若存在，求的值；若不存在，请说明理由.
题型03平行：面面平行探索性
【解题攻略】
【典例1-1】在三棱柱中，
(1)若 分别是的中点，求证：平面平面.
(2)若点分别是上的点，且平面平面，试求的值．
【变式1-1】.在长方体中，，P为的中点．已知过点的平面与平面平行，平面与直线分别相交于点M，N，请确定点M，N的位置；
【变式1-2】已知正方体中，､分别为对角线､上的点，且．
（1）求证：平面；
（2）若是上的点，的值为多少时，能使平面平面？请给出证明．
题型04 垂直：线面垂直探索性
【解题攻略】
【典例1-1】已知正方体的棱长为，、、分别是、、的中点．
(1)求证：平面；
(2)在线段上是否存在点，使得平面？若存在，求线段的长；若不存在，请说明理由；
(3)求到平面的距离．
【变式1-1】如图，在四棱锥S－ABCD中，四边形ABCD是边长为2的菱形，∠ABC＝60°，△SAD为正三角形．侧面SAD⊥底面ABCD，E，F分别为棱AD，SB的中点．
(1)求证：AF∥平面SEC；
(2)求证：平面ASB⊥平面CSB；
(3)在棱SB上是否存在一点M，使得BD⊥平面MAC？若存在，求的值；若不存在，请说明理由．
【变式1-2】如图，在直三棱柱中，，，，为棱上靠近的三等分点，为棱上靠近的三等分点.
(1)证明：平面；
(2)在棱上是否存在点D，使得面?若存在，求出的大小并证明；若不存在，说明理由.
题型05垂直：面面垂直翻折探索性
【解题攻略】
【典例1-1】
如图，在四棱锥P－ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝，AD＝CD＝1，∠ADC＝120°，点M是AC与BD的交点，点N在线段PB上，且PN＝PB.
(1)证明：MN平面PDC；
(2)在线段BC上是否存在一点Q，使得平面MNQ⊥平面PAD，若存在，求出点Q的位置；若不存在，请说明理由.
【变式1-1】如图，在三棱台ABC­DEF中，CF⊥平面DEF，AB⊥BC.
(1)设平面ACE∩平面DEF＝a，求证：DF∥a；
(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在，请确定G点的位置；若不存在，请说明理由．
【变式1-2】如图（1），点E是直角梯形ABCD底边CD上的一点，∠ABC＝90°，BC＝CE＝1，AB＝DE＝2，将沿AE折起，使得D－AE－B成直二面角，连接CD和BD，如图（2）．
(1)求证：平面平面BCD；
(2)在线段BD上确定一点F，使得平面ADE.
题型06证明与建系：斜棱柱垂面法建系
【解题攻略】
【典例1-1】（2023·四川成都·校联考模拟预测）如图，在三棱柱中，平面平面ABC，，，，，，．

(1)求证：B，D，E，四点共面；
(2)求二面角的余弦值．
【变式1-1】（2023·河北沧州·校考模拟预测）如图，在斜三棱柱中，，，的中点为，的中点为.

(1)证明：OD∥平面；
(2)若，，，求平面与平面所成角的大小.
【变式1-2】（2023·安徽滁州·安徽省定远中学校考二模）如图，在三棱柱中，四边形是边长为4的菱形．，点D为棱AC上动点(不与A，C重合)，平面B1BD与棱A1C1交于点E．
(1)求证：；
(2)若，平面ABC⊥平面，，求直线BC与平面B1BDE所成角的正弦值．
题型07证明与建系：斜棱柱垂线法建系
【典例1-1】（2023·广东韶关·统考模拟预测）如图，在三棱柱中，为的中点，，，，点在底面上的射影为点.

(1)求证：平面；
(2)若，求平面与平面所成角的正弦值.
【变式1-1】（2023·四川成都·川大附中校考模拟预测）如图所示多面体ABCDEF中，平面平面ABCD，平面ABCD，是正三角形，四边形ABCD是菱形，，，
(1)求证：平面ABCD；
(2)求二面角的正弦值.
【变式1-2】（2023·福建福州·福州三中校考模拟预测）如图，在三棱柱中，，侧面为菱形，为等边三角形．
(1)求证：；
(2)若，点E是侧棱上的动点，且平面与平面的夹角的余弦值为，求点B到平面的距离．
题型08 证明与建系：三棱锥投影法建系
【典例1-1】（2023春·江苏南通·高三统考期末）如图，在三棱锥中，，D是AC的中点，E是AB上一点，平面PDE.
(1)证明：平面PBC；
(2)若，，求二面角的正弦值．
【变式1-1】（2023·贵州贵阳·高三贵阳一中校考阶段练习）如图，在三棱锥中，是点在平面ABC上的投影，，，是BD的中点.
(1)证明：平面DAC；
(2)若O点正好落在的内角平分线上，，，，求二面角的正弦值.
【变式1-2】（2023·全国·高三专题练习）在三棱锥中，D，E，P分别在棱AC，AB，BC上，且D为AC中点，，于F.
(1)证明：平面平面；
(2)当，，二面角的余弦值为时，求直线与平面所成角的正弦值.
题型09 证明与建系：角平分线法建系
【解题攻略】
【典例1-1】（2024年九省联考）如图，平行六面体中，底面是边长为2的正方形，为与的交点，．
（1）证明：平面；
（2）求二面角的正弦值．
【变式1-1】（2023·河南·校联考模拟预测）已知三棱柱中，是的中点，是线段上一点.

(1)求证：；
(2)设是棱上的动点（不包括边界），当的面积最小时，求直线与平面所成角的正弦值.
【变式1-2】(2024郑州一质检）如图，在多面体中，底面为平行四边形，平面BC，为等边三角形，．
(1)求证：平面平面；
(2)求平面与平面夹角的余弦值．
题型10二面角延长线法
【典例1-1】.（2023春·安徽芜湖·高三统考）在三棱锥中，底面是边长为2的等边三角形，且直线与平面所成角为为中点.

(1)求证：平面平面；
(2)求二面角的正弦值.
【变式1-1】（2023·广东佛山·校考模拟预测）如图，在三棱锥中，
，设点为上的动点.

(1)求面积的最小值；
(2)求平面与平面的夹角的余弦值.
【变式1-2】（2023秋·河南郑州·高三郑州外国语学校校考阶段练习）如图，在三棱锥中，，，，，二面角为钝角，三棱锥的体积为.

(1)求二面角的大小；
(2)求直线AP与平面PBC所成角的正弦值.
.
题型11翻折型
【解题攻略】
【典例1-1】（2023·福建三明·统考三模）如图，平面五边形由等边三角形与直角梯形组成，其中，，，，将沿折起，使点到达点的位置，且.

(1)当时，证明并求四棱锥的体积；
(2)已知点为棱上靠近点的三等分点，当时，求平面与平面夹角的余弦值.
【变式1-1】（2023·辽宁·辽宁实验中学校考模拟预测）已知直角梯形形状如下，其中，，，．

(1)在线段CD上找出点F，将四边形沿翻折，形成几何体．若无论二面角多大，都能够使得几何体为棱台，请指出点F的具体位置（无需给出证明过程）．
(2)在（1）的条件下，若二面角为直二面角，求棱台的体积，并求出此时二面角的余弦值．
【变式1-2】（2023·福建厦门·统考模拟预测）筝形是指有一条对角线所在直线为对称轴的四边形．如图，四边形为筝形，其对角线交点为，将沿折到的位置，形成三棱锥．

(1)求到平面的距离；
(2)当时，在棱上是否存在点，使得直线与平面所成角的正弦值为？若存在，求的值；若不存在，请说明理由．
题型12台体型
【解题攻略】
【典例1-1】．（2019上·浙江·高三校联考）在三棱台中，是等边三角形，二面角的平面角为，.
（I）求证：；
（II）求直线与平面所成角的正弦值.
【变式1-1】（2024上·山东德州·高三统考）如图，在四棱台中，底面是边长为2的菱形，，，点分别为的中点．
(1)证明：直线面；
(2)求二面角的余弦值．
【变式1-2】（2023·河南·襄城高中校联考模拟预测）如图，在正四棱台中，，，，为棱，的中点，棱上存在一点，使得平面．

(1)求；
(2)当正四棱台的体积最大时，求与平面所成角的正弦值．
高考练场 高考练场
1.如图，四棱锥的底面是平行四边形，设平面与平面的交线为直线．证明：平面.
2.如图，在正方体中，为的中点．
(1)求证：平面；
(2)上是否存在一点，使得平面平面，若存在，请说明理由．
3..如图，四棱锥中，，，为的中点．
(1)求证：平面.
(2)在线段上是否存在一点，使得平面平面？若存在，证明你的结论，若不存在，请说明理由．
4..如图，在四棱锥中，侧棱底面，底面是直角梯形，，，且，，是的中点．
(1)求证：平面；
(2)在线段上是否存在一点，使得平面？若存在，求出的值；若不存在，请说明理由．
5.图1是由矩形，和菱形组成的一个平面图形，其中，，，将其沿，折起使得与重合，连接，如图2.
(1)证明：图2中的，，，四点共面，且平面平面；
(2)求图2中的直线与平面所成角的正弦值.
6.（2023·四川宜宾·宜宾市叙州区第一中学校校考模拟预测）如图，在三棱柱中，．

(1)证明：；
(2)若，且，求二面角的正弦值．
7.（2023·江西南昌·统考二模）如图，在四棱锥中，底面是边长为4的菱形，，，点E在线段上，，平面平面．
(1)求；
(2)求直线与平面所成角的正弦值．
8.（2023·全国·高三专题练习）如图，在三棱锥P－ABC中，AB＝AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．已知BC＝8，PO＝4，AO＝3，OD＝2.
(1)证明：AP⊥BC；
(2)若点M是线段AP上一点，且AM＝3，试证明AM⊥平面BMC.
9.（2022·江西·校联考模拟预测）如图，在三棱柱中，，，．
(1)求证：；
(2)若为线段的中点，求直线与平面所成角的正弦值．
10.（2023·河南新乡·统考三模）如图，在多面体ABCDEF中，四边形ABCD是正方形，是等边三角形，，，M是AD的中点.
(1)证明：平面ECD.
(2)当二面角为时，求二面角的余弦值.
.
11.（2022下·浙江杭州·高三浙江大学附属中学校考阶段练习）如图，在四棱台中，底面四边形是菱形，面，且，E是棱的中点．
(1)求证：；
(2)求多面体（四棱台切掉三棱锥剩下的部分）的体积；
(3)求直线与平面所成线面角的正弦值．
12.（2022·浙江·校联考模拟预测）如图，在四棱台中，底面为正方形，H在棱上，，．
(1)求证：平面；
(2)若M为的中点，且，求直线和平面所成角的正弦值．
两个平面相交：
1.两点确定一条直线，只需确定两平面的两个公共点即可
2.由于两平面有一个公共点A，再找一个公共点即可确定交线
3.一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行，在平面内，过两平面的公共点作直线与已知直线平行，则此直线即为两平面的交线
平行的常用构造方法
①三角形中位线法；
②平行四边形线法；
③比例线段法.
注意：平行构造主要用于：①异面直线求夹角；②平行关系的判定.
证明平行
(1)线线平行：设直线l1和l2的方向向量分别为v1和v2，则l1∥l2(或l1与l2重合)⇔v1∥v2.
(2)线面平行：设直线l的方向向量为v，平面α的法向量为u，则l∥α或l⊂α⇔v⊥u.
(3)面面平行：设平面α和β的法向量分别为u1，u2，则α∥β⇔u1 ∥u2.
垂直的常见构造：
①等腰三角形三线合一法；
②勾股定理法；
③投影法.
④菱形的对角线互相垂直
翻折
翻折前后，在同一平平面内的点线关系不变
翻折过程中是否存在垂直或者平行等特殊位置关系
翻折过程中，角度是否为定值
翻折过程中，体积是否存在变化
斜棱柱垂线型建系
如果存在垂线（投影型）斜棱柱，则可以直接借助垂线作为z轴建系，下底面，可以寻找或者做出一对垂线作为xy轴。这类建系，主要难点是分析“空中”的点的坐标。空中点坐标可以有以下思维：
让空中点垂直砸下来（落下来，寻找投影），投影点坐标以及下落的高度
借助向量相等，寻找空中点所在线段的向量对应的底面相等向量，即可计算出空中点的坐标
等角射影平分线型建系
如果一条线和一个角的两边所成角度相等，则该线在角度所在平面射影是角平分线。此时，这个模型也满足“三面角余弦定理”：
大题解答时，需要简单的证明才能使用
翻折型建系
翻折型几何体，寻找翻折前和翻折后的“变与不变”的点线面关系。
翻折前翻折后在同一平面内的点线，数量关系不变。
翻折后，一般情况下是存在垂直的平面，可以利用垂面法建系计算
翻折后，可以构造三棱锥，利用三棱锥斜面建系法来建系计算
台体建系型
正棱台型，建系较简单，一般是正多边形中心作为原点，上下底面连线作为z轴。
非正棱台型，如有垂面或者垂线，则可以垂面垂线型建系，无垂面垂线，则可参考三棱锥斜面建系思维。
第二十讲 立体几何大题综合归类
目录
TOC \ "1-1" \h \u \l "_Tc31183" 题型01平行：无交线型 PAGEREF _Tc31183 \h 1
\l "_Tc15411" 题型02平行：线面平行探索性 PAGEREF _Tc15411 \h 5
\l "_Tc19920" 题型03平行：面面平行探索性 PAGEREF _Tc19920 \h 8
\l "_Tc30670" 题型04 垂直：线面垂直探索性 PAGEREF _Tc30670 \h 10
\l "_Tc25026" 题型05垂直：面面垂直翻折探索性 PAGEREF _Tc25026 \h 14
\l "_Tc7885" 题型06证明与建系：斜棱柱垂面法建系 PAGEREF _Tc7885 \h 17
\l "_Tc7905" 题型07证明与建系：斜棱柱垂线法建系 PAGEREF _Tc7905 \h 20
\l "_Tc16696" 题型08 证明与建系：三棱柱投影法建系 PAGEREF _Tc16696 \h 24
\l "_Tc23017" 题型09 证明与建系：角平分线法建系 PAGEREF _Tc23017 \h 27
\l "_Tc6755" 题型10二面角延长线法 PAGEREF _Tc6755 \h 31
\l "_Tc23619" 题型11翻折型 PAGEREF _Tc23619 \h 34
\l "_Tc25583" 题型12台体型 PAGEREF _Tc25583 \h 38
\l "_Tc8054" 高考练场 PAGEREF _Tc8054 \h 42
热点题型归纳
题型01平行：无交线型
【解题攻略】
【典例1-1】如图，在平行四边形中，，，为的中点，以为折痕将折起，使点到达点的位置，且，，分别为，的中点.
(1)证明：平面.
(2)若平面与平面的交线为，求直线与平面所成角的正弦值.
【答案】(1)证明见解析；(2).
【分析】（1）连接，交于，并连接，易得为正方形，进而知为中位线，则，最后根据线面平行的判定证结论；
（2）若为中点，连接，由线面、面面垂直的判定可证面面，从而在面上的射影在直线上，过作直线则有直线为面与面的交线，故与面所成角即为所求角，再根据已知、等体积法求到面的距离，即可求角的正弦值.
（1）
连接，交于，并连接，
由、分别是、的中点，而，故为正方形，
所以为的中点，又是的中点，
所以，而面，面，故面.
（2）
由题易知：且均为等腰三角形，且均为等边三角形，
若为中点，连接，则，
而，面，则面，
又面，故面面，面面，
所以在面上的射影在直线上，
过作直线，而，则，故直线为面与面的交线，
所以直线与平面所成角，即为与面所成角，
由题设，，，令，则，，
因为面，面，故，
所以，又，易知，
在△中，，整理得，
所以，故，，
若到面的距离为，且，即，
所以，，，，
综上，，则.
【变式1-1】如图所示，在四棱柱中，底面是等腰梯形，，,,侧棱⊥底面且．
(1)指出棱与平面的交点的位置（无需证明）；
(2)求点到平面的距离．
【答案】(1)点位于的中点位置，理由见解析；
(2).
【分析】（1）作出辅助线，得到四棱柱为长方体，利用中位线得到线线平行，得到棱与平面的交点的位置为的中点；
（2）利用等体积法求解点到平面的距离.
（1）
延长至点F，且DF=CD，延长至点H，使得，连接FH，交于点Q，
因为四棱柱中，底面是等腰梯形，，
所以四棱柱为长方体，，且为的中点，
取的中点E，连接ED，则，
所以，
故棱与平面的交点的位置为的中点；
（2）
取AB的中点M，连接DM，
因为,,
故△ADM为等边三角形，
所以，
因为侧棱⊥底面且，平面，
所以，
由勾股定理得：，
由余弦定理得：，
其中，
，
由余弦定理得：，
因为，
所以，
由三角形面积公式可知：，
设点到平面的距离为，
因为，即，
，解得：，
所以点到平面的距离为.
【变式1-2】如图，为圆锥的顶点，为圆锥底面的圆心，圆锥的底面直径，母线，是的中点，四边形为正方形．设平面平面，证明：；
【答案】证明见解析.
【分析】利用线面平行的判定定理可得平面，再利用线面平行的性质定理即得.
【详解】因为四边形为正方形，
∴，
∵平面，平面，
∴平面，
∵平面，平面平面，
∴．
.
题型02平行：线面平行探索性
【解题攻略】
【典例1-1】如图，在三棱柱中，侧面底面，，，且，为中点.
(1)求证平面
(2)在上是否存在一点，使得平面，若不存在，说明理由；若存在，确定点E的位置.
【答案】(1)证明见解析。(2)存在，E为线段BC1的中点
【分析】（1）利用线面垂直的判定定理进行证明即可；
（2）连接，交于，连接，能够判断OM平面A1AB，BC1的中点M即为所求的E点.
（1）证明：连接，，且为的中点，所以.
，且为的中点，∴A1O⊥AC.又，平面，平面，
∴平面．
（2）存在点E，且E为线段BC1的中点.理由：连接，交于，连接，则OM是的一条中位线，OMAB1，
又平面，OM⊄平面A1AB，∴OM平面A1AB，故BC1的中点M即为所求的E点.
【变式1-1】如图，四边形中，，，，，，分别在，上，，现将四边形沿折起，使．
(1)若，在折叠后的线段上是否存在一点，使得平面？若存在，求出的值；若不存在，说明理由.
(2)求三棱锥的体积的最大值，并求出此时点到平面的距离.
【答案】(1)存在，
(2)三棱锥A­CDF的体积的最大值为3，此时点F到平面ACD的距离为
【分析】(1)在AD上取一点P，使得，证明线面平行，则P点就是所求的点；
(2)先设 ，运用二次函数即可求出三棱锥 的体积最大值，再运用等体积法求出F到平面ACD的距离.
（1）
AD上存在一点P，使得CP 平面ABEF，此时，
理由如下：当时，，如图，过点P作M FD交AF于点M，连接ME，则，
∵BE＝1，∴FD＝5，∴MP＝3，又EC＝3，MP FD EC，∴MP EC，
故四边形MPCE为平行四边形，∴CP ME，又CP⊄平面ABEF，ME⊂平面ABEF，
∴CP 平面ABEF；
（2）设BE＝x，则AF＝x(0