2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)02挑战压轴题(填空题)(原卷版+解析)

这是一份2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)02挑战压轴题(填空题)(原卷版+解析)，共29页。


1． (2023·安徽）设抛物线，其中a为实数．
（1）若抛物线经过点，则______；
（2）将抛物线向上平移2个单位，所得抛物线顶点的纵坐标的最大值是______．
2．（安徽省2020年中考数学试题）在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片沿过点的直线折叠，使得点落在上的点处，折痕为；再将分别沿折叠，此时点落在上的同一点处．请完成下列探究：
的大小为__________；
当四边形是平行四边形时的值为__________．
3．（安徽省2019年中考数学试题）在平面直角坐标系中，垂直于x轴的直线l分别于函数y=x-a+1和y=x2-2ax的图像相交于P，Q两点.若平移直线l，可以使P，Q都在x轴的下方，则实数a的取值范围是_______
5． (2023·安徽）在三角形纸片ABC中，，，.将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去后得到双层（如图2），再沿着边某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为_________cm.
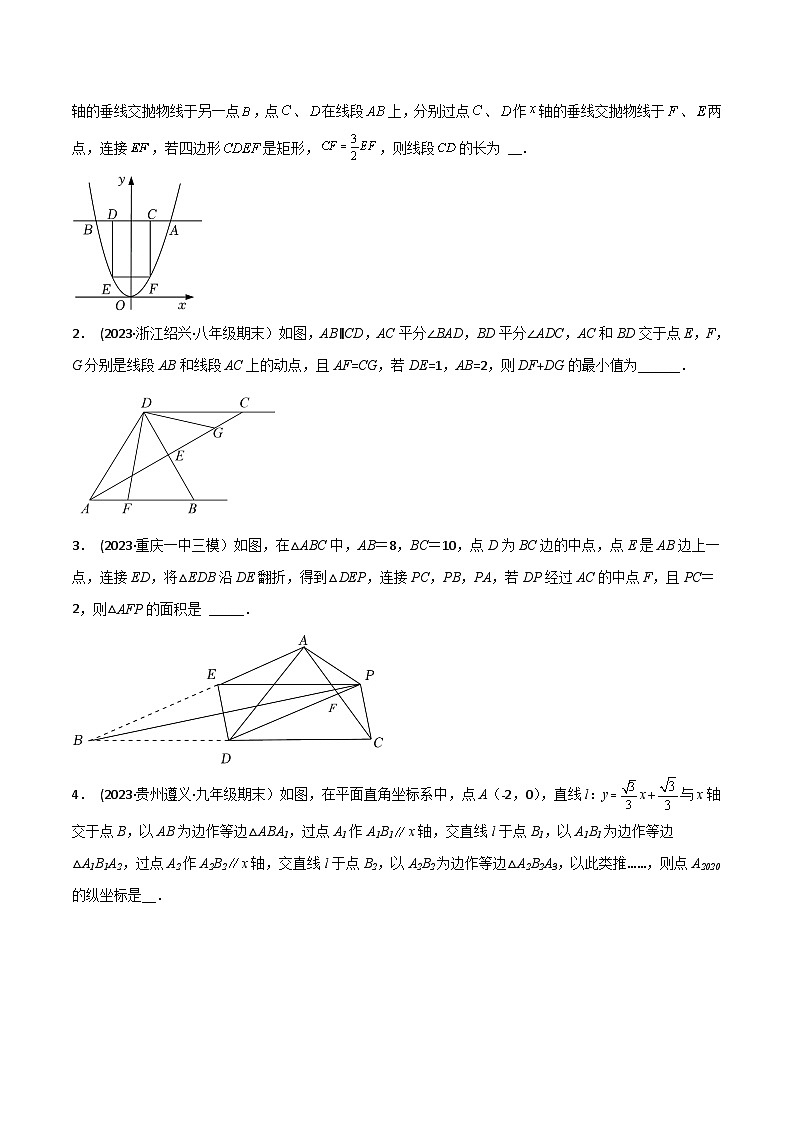
1． (2023·吉林·九年级期末）如图，在平面直角坐标系中，点在抛物线上，过点作轴的垂线交抛物线于另一点，点、在线段上，分别过点、作轴的垂线交抛物线于、两点，连接，若四边形是矩形，，则线段的长为 __．
2． (2023·浙江绍兴·八年级期末）如图，AB∥CD，AC平分∠BAD，BD平分∠ADC，AC和BD交于点E，F，G分别是线段AB和线段AC上的动点，且AF=CG，若DE=1，AB=2，则DF+DG的最小值为______．
3． (2023·重庆一中三模）如图，在△ABC中，AB＝8，BC＝10，点D为BC边的中点，点E是AB边上一点，连接ED，将△EDB沿DE翻折，得到△DEP，连接PC，PB，PA，若DP经过AC的中点F，且PC＝2，则△AFP的面积是 _____．
4． (2023·贵州遵义·九年级期末）如图，在平面直角坐标系中，点A（﹣2，0），直线l：yx与x轴交于点B，以AB为边作等边△ABA1，过点A1作A1B1x轴，交直线l于点B1，以A1B1为边作等边△A1B1A2，过点A2作A2B2x轴，交直线l于点B2，以A2B2为边作等边△A2B2A3，以此类推……，则点A2020的纵坐标是__．
5． (2023·河南南阳·三模）如图，在等腰三角形ABC中，AB＝AC，延长BC到点D，菱形CDEF的边CF在边AC上，过点F作FG∥AB交BE于点G，点G是BE的中点，如果∠A＝60°，则线段EF和BC的数量关系为____，如果∠A＝90°，AB＝2＋2，则CD的长为____．
1． (2023·河南濮阳·一模）如图，有一张矩形纸条ABCD，AB＝5，,点M，N分别在边AB，CD，CN＝1．现将四边形BCNM沿MN折叠，使点B，C分别落在点， 处，在点M从点A运动到点B的过程中，若边与边CD交于点E，则点E相应运动的路径长___．
2． (2023·安徽安庆·九年级开学考试）如图．直线与坐标轴相交于A、B两点，动点P在线段AB上，动点Q在线段OA上、连结OP，且满足，则当______度时，线段OQ的最小值为______．
3． (2023·四川巴中·九年级期末）如图，在矩形ABCD中，对角线AC与BD相交于点O，AB＝3，BC＝4，将△ABO沿着AC折叠得到ΔAB′O，B′O与AD相交于点E，则OE的长是______．
4． (2023·广东·模拟预测）在平面直角坐标系xOy中，已知，，三点，其中，函数的图象分别与线段BC，AC交于点P，Q．若，则t的值为______．
5． (2023年浙江省宁波市中考数学模拟预测数学试题）太极推盘是一种常见的健身器材（如图1），转动两个圆盘便能锻炼身体．取推盘上半径均为0.4米的圆A与圆B（如图2）且AB=1米，圆A绕圆心A以2°每秒的速度逆时针旋转，圆B绕圆心B以2°每秒的速度顺时针旋转．开始转动时圆A上的点C恰好落在线段AB上，圆B上的点D在AB下方且满足∠DBA=60°，则在两圆同时开始转动的30秒内，CD的最小值是_______米．
2024年中考数学冲刺 挑战压轴题专题汇编（安徽考卷）
02挑战压轴题（填空题）
1． (2023·安徽）设抛物线，其中a为实数．
（1）若抛物线经过点，则______；
（2）将抛物线向上平移2个单位，所得抛物线顶点的纵坐标的最大值是______．
【答案】 0 2
【解析】
【分析】
（1）直接将点代入计算即可
（2）先根据平移得出新的抛物线的解析式，再根据抛物线顶点坐标得出顶点坐标的纵坐标，再通过配方得出最值
【详解】
解：（1）将代入得：
故答案为：0
（2）根据题意可得新的函数解析式为：
由抛物线顶点坐标
得新抛物线顶点的纵坐标为：
∵
∴当a=1时，有最大值为8，
∴所得抛物线顶点的纵坐标的最大值是
故答案为：2
【点睛】
本题考查将抛物线的顶点坐标、将点代入代入函数解析式、利用配方法求最值是常用的方法
2．（安徽省2020年中考数学试题）在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片沿过点的直线折叠，使得点落在上的点处，折痕为；再将分别沿折叠，此时点落在上的同一点处．请完成下列探究：
的大小为__________；
当四边形是平行四边形时的值为__________．
【答案】30
【分析】
（1）根据折叠得到∠D+∠C=180°，推出AD∥BC，，进而得到∠AQP=90°，以及∠A=180°-∠B=90°，再由折叠，得到∠DAQ=∠BAP=∠PAQ=30°即可；
（2）根据题意得到DC∥AP，从而证明∠APQ=∠PQR，得到QR=PR和QR=AR，结合（1）中结论，设QR=a，则AP=2a，由勾股定理表达出AB=AQ=即可解答．
【详解】
解：（1）由题意可知，∠D+∠C=180°，
∴AD∥BC，
由折叠可知∠AQD=∠AQR，∠CQP=∠PQR，
∴∠AQR+∠PQR=，即∠AQP=90°，
∴∠B=90°，则∠A=180°-∠B=90°，
由折叠可知，∠DAQ=∠BAP=∠PAQ，
∴∠DAQ=∠BAP=∠PAQ=30°，
故答案为：30；
（2）若四边形APCD为平行四边形，则DC∥AP，
∴∠CQP=∠APQ，
由折叠可知：∠CQP=∠PQR，
∴∠APQ=∠PQR，
∴QR=PR，
同理可得：QR=AR，即R为AP的中点，
由（1）可知，∠AQP=90°，∠PAQ=30°，且AB=AQ，
设QR=a，则AP=2a，
∴QP=，
∴AB=AQ=，
∴，
故答案为：．
【点睛】
本题考查了四边形中的折叠问题，涉及了平行四边形的性质，勾股定理等知识点，解题的关键是读懂题意，熟悉折叠的性质．
3．（安徽省2019年中考数学试题）在平面直角坐标系中，垂直于x轴的直线l分别于函数y=x-a+1和y=x2-2ax的图像相交于P，Q两点.若平移直线l，可以使P，Q都在x轴的下方，则实数a的取值范围是_______
【答案】a＞1或a＜-1
【解析】
【分析】
首先求出y=x-a+1＜0和y=x2-2ax＜0的解集，然后分情况讨论，联立不等式，即可得到a的取值范围.
【详解】
解：∵直线l分别与函数y=x-a+1和y=x2-2ax的图像相交于P，Q两点，且都在x轴的下方，
∴令y=x-a+1＜0，解得x＜a-1，
令y=x2-2ax＜0，当a＞0时,解得：0＜x＜2a；当a＜0时，解得：2a＜x＜0，
①当a＞0时，若有解，则，解得：a＞1，
②当a＜0时，若有解，则，解得：a＜-1，
综上所述，实数a的取值范围是a＞1或a＜-1.
【点睛】
本题考查了一次函数、二次函数与不等式的关系，利用数形结合与分类讨论思想是解题关键.
4．（安徽省2018年中考数学试题）矩形ABCD中，AB=6，BC=8.点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC，若△APD是等腰三角形，则PE的长为数___________.
【答案】3或1.2
【分析】
由△PBE∽△DBC，可得∠PBE=∠DBC，继而可确定点P在BD上，然后再根据△APD是等腰三角形，分DP=DA、AP=DP两种情况进行讨论即可得.
【详解】
∵四边形ABCD是矩形，∴∠BAD=∠C=90°，CD=AB=6，BC=8，∴BD=10，
∵△PBE∽△DBC，
∴∠PBE=∠DBC，∴点P在BD上，
如图1，当DP=DA=8时，BP=2，
∵△PBE∽△DBC，
∴PE：CD=PB：DB=2：10，
∴PE：6=2：10，
∴PE=1.2；
如图2，当AP=DP时，此时P为BD中点，
∵△PBE∽△DBC，
∴PE：CD=PB：DB=1：2，
∴PE：6=1：2，
∴PE=3；
综上，PE的长为1.2或3，
故答案为1.2或3.
【点睛】
本题考查了相似三角形的性质，等腰三角形的性质，矩形的性质等，确定出点P在线段BD上是解题的关键.
5． (2023·安徽）在三角形纸片ABC中，，，.将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去后得到双层（如图2），再沿着边某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为_________cm.
【答案】或
【解析】
【详解】
试题解析：先判断该平行四边形是菱形，在求出周长，注意分类讨论.（1）作
所得的平行四边形的周长为40cm.
（2）作
所得的平行四边形的周长为cm.
考点： 菱形的判定及性质.
1． (2023·吉林·九年级期末）如图，在平面直角坐标系中，点在抛物线上，过点作轴的垂线交抛物线于另一点，点、在线段上，分别过点、作轴的垂线交抛物线于、两点，连接，若四边形是矩形，，则线段的长为 __．
【答案】2
【解析】
【分析】
利用待定系数法求出抛物线解析式，设点横坐标为，点C（m,4），根据四边形是矩形，可证EF∥x轴，F、E两点纵坐标相同，根据、两点在抛物线上，得出F，E关于y轴对称，可证点C与点D关于y轴对称，得出点D的坐标为(-m，4)根据，求出点坐标为，根据函数解析式列方程，解方程即可．
【详解】
解：把代入中得，
解得，
，
设点横坐标为，点C（m,4），
∵四边形是矩形，
∴EF∥CD即EF∥AB，
过点A作轴的垂线交抛物线于另一点，
∴AB∥x轴，
∴EF∥x轴，F、E两点纵坐标相同，
∵、两点在抛物线上，
∴F，E关于y轴对称，
∴点C与点D关于y轴对称，
∴点D的坐标为(-m，4)，
则，
，
，
点坐标为，
，
解得（舍或．
．
故答案为：2．
【点睛】
本题考查待定系数法求抛物线解析式，矩形性质，轴对称判定与性质，根据矩形性质得出FE∥x轴，利用点F的坐标特征列方程是解题关键．
2． (2023·浙江绍兴·八年级期末）如图，AB∥CD，AC平分∠BAD，BD平分∠ADC，AC和BD交于点E，F，G分别是线段AB和线段AC上的动点，且AF=CG，若DE=1，AB=2，则DF+DG的最小值为______．
【答案】
【解析】
【分析】
先根据AC平分∠BAD，BD平分∠ADC，AB∥CD证明四边形ABCD是菱形．在AC上取点B'，使AB'=AB，连接FB'，作点D关于AB的对称点D'，连接D'F、DD'．作BH⊥CD于点H，作BM⊥DD'于点M，则△B'AF≌△DCG（SAS），得出B'F=DG，所以DF+DG=D'F+B'F，当B'、F、D'三点在同一直线上时，DF+DG=D'F+B'F取最小值为B'D'．再根据勾股定理求出B'D'即可．
【详解】
解：连接BC，
∵AC平分∠BAD，BD平分∠ADC，AB∥CD，
∴∠DAC=∠BAC，∠ADB=∠CDB，∠AED=180°-180°÷2=90°，
∵AB∥CD，
∴∠DCA=∠BAC，
∴∠DCA=∠DAC，
∴DA=DC，
同理：DA=BA，
∴DC=AB，
∵AB∥CD，
∴四边形ABCD是平行四边形，
∵DA=DC，
∴四边形ABCD是菱形．
如图．在AC上取点B'，使AB'=AB，连接FB'，作点D关于AB的对称点D'，连接D'F、DD'．
作B'H⊥CD于点H，作B'M⊥DD'于点M．
∴DF=D'F，
∵AF=CG，∠B'AF=∠DCG，AB'=AB=CD，
∴△B'AF≌DCG（SAS），
∴B'F=DG，
∴DF+DG=D'F+B'F，
∴当B'、F、D'三点在同一直线上时，DF+DG=D'F+B'F取最小值为B'D'．
∵DE=1，AD=AB=2，
∴∠DAE=30°，∠ADE=60°，
∴AC=AD=2，CB'=2-2，
∴B'H=B'C=-1，CH=B'H=3-，
∴DH=DC-CH=2-（3-）=−1，
∵四边形DHB′M是矩形
∴DM=B'H=-1，MB′=DH=,
∴D'M=DD'-DM=AD-DM=2-（-1）=+1，
∴D'B'=．
即DF+DG的最小值为2．
故答案为：．
【点睛】
本题考查了线段之和最小值问题，作辅助线推出△B'AF≌△DCG是解题的关键．
3． (2023·重庆一中三模）如图，在△ABC中，AB＝8，BC＝10，点D为BC边的中点，点E是AB边上一点，连接ED，将△EDB沿DE翻折，得到△DEP，连接PC，PB，PA，若DP经过AC的中点F，且PC＝2，则△AFP的面积是 _____．
【答案】##
【解析】
【分析】
过点D作 DM⊥AB于点M，设ED与BP交于点O，可得四边形BDPE为平行四边形，而BD＝DP，故平行四边形BDPE为菱形，即得EP＝BD＝BE＝CD＝5，BP⊥ED，又四边形 EPCD为平行四边形，推出ED＝PC＝2，证明四边形EDPG是平行四边形，可得PF是△ACG中位线，从而PFAG＝1，在 Rt△BOE中，BO＝2，即知S△BDEDE•BO＝2BE•DM，推出DM，根据△AFP与△BDE等高，即可得答案．
【详解】
解：过点D作 DM⊥AB于点M，设ED与BP交于点O，
∵点D是BC边的中点，点F是AC的中点，
∴DP∥BE，
∴∠EBD＝∠PDC，
又∵∠EPD＝∠EBD，
∴∠EPD＝∠PDC，
∴EP∥BD，
∴四边形BDPE为平行四边形，
又∵BD＝DP，
∴平行四边形BDPE为菱形，
∴EP＝BD＝BE＝DP＝CD＝5，BP⊥ED，
∴四边形 EPCD为平行四边形，
∴ED＝PC＝2，ED∥CP，
∵DP∥BE，即DP∥EG，
∴四边形EDPG是平行四边形，
∴EG＝DP＝5，PG＝ED＝2，
∴PG＝CP，
∴PF是△ACG中位线，
∵AE＝AB﹣BE＝8﹣5＝3，
∴AG＝EG﹣AE＝5﹣3＝2，
∴PFAG＝1，
在 Rt△BOE中，
BE＝BD＝5，EODE＝1，
∴BO2，
∴S△BDEDE•BO＝2BE•DM，
∴DM，
∵平行线间的距离相等，△AFP以PF为底，高即为，
∴S△AFPPF1，
故答案为：．
【点睛】
本题属于四边形综合题，考查了菱形的判定和性质，全等三角形的判定和性质，勾股定理，三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题．
4． (2023·贵州遵义·九年级期末）如图，在平面直角坐标系中，点A（﹣2，0），直线l：yx与x轴交于点B，以AB为边作等边△ABA1，过点A1作A1B1x轴，交直线l于点B1，以A1B1为边作等边△A1B1A2，过点A2作A2B2x轴，交直线l于点B2，以A2B2为边作等边△A2B2A3，以此类推……，则点A2020的纵坐标是__．
【答案】
【解析】
【分析】
先根据解析式求得B的坐标，即可求得AB＝1，根据等边三角形的性质以及含30°角的直角三角形的性质，分别求得A1的纵坐标为，A2的纵坐标为，A3的纵坐标为，进而得到An的纵坐标为，据此可得点A2020的纵坐标．
【详解】
∵直线l：yx与x轴交于点B，
令y=0，即yx=0，解得：x=−1
∴B（﹣1，0），
∴OB＝1，
∵A（﹣2，0），
∴OA＝2，
∴AB＝1，
∵△ABA1是等边三角形，过A1点作于 ，如图所示，
则，，
∴，
∴A1（，），
∵∥AB，
∴把y代入yx，求得x，
∴B1（，），
∴A1B1＝2，
过A2点作于 ，
∵△是等边三角形
则是的中点，且
∴C2点的横坐标为：，
∵，
∴A2（，），即A2（，），
∵A3B3∥AB，
∴把y代入yx，得x，
∴B2（，），
∴A2B2＝4，
过A3点作于 ，
∵△是等边三角形，
则是的中点，且
∴C3点的横坐标为：，
∵，
∴A3（，），
即A3（ ，），
一般地，An的纵坐标为，
∴点A2020的纵坐标是，
故答案为．
【点睛】
本题是规律探索题，考查了一次函数的图象，等边三角形的性质，从特殊出发得到一般性结论是本题的关键．
5． (2023·河南南阳·三模）如图，在等腰三角形ABC中，AB＝AC，延长BC到点D，菱形CDEF的边CF在边AC上，过点F作FG∥AB交BE于点G，点G是BE的中点，如果∠A＝60°，则线段EF和BC的数量关系为____，如果∠A＝90°，AB＝2＋2，则CD的长为____．
【答案】 BC＝2EF
【解析】
【分析】
延长FG交BC于点M，利用ASA证明△BGM≌△EGF，当∠A＝60°时，证明△ABC和△MCF为等边三角形，再利用菱形的性质，即可得到EF和BC的数量关系；当∠A＝90°，AB＝2+2时，先证明△ABC和△MCF为等腰直角三角形，利用等腰直角三角形的边角关系即可得到菱形的边长．
【详解】
解：如图，延长FG交BC于点M，
∵四边形CDEF为菱形，
∴EF∥BC，
∴∠GBM＝∠GEF，
∵BG＝GE，∠BGM＝∠EGF，
∴△BGM≌△EGF（ASA），
∴BM＝EF，
设菱形CDEF的边长为a，则BM＝EF＝a，
在等腰三角形ABC中，AB＝AC，如果∠A＝60°，则△ABC为等边三角形，
∴∠A＝∠ABC＝∠ACB＝60°，
∵FG∥AB，
∴∠FMC＝∠ABC＝60°，∠CFM＝∠A＝60°，
∴△FMC为等边三角形，
∴MC＝CF＝a，
∴BC＝BM+MC＝2a，
∴BC＝2EF，
在等腰三角形ABC中，AB＝AC，如果∠A＝90°，则△ABC为等腰直角三角形，
∴BC＝AB＝（2+2）＝4+2，∠ACB＝45°，
∴MC＝BC﹣BM＝4+2﹣a，
∵FG∥AB，
∴FG⊥AC，
∴△FMC为等腰直角三角形，
∴MC＝CF＝a，
∴4+2﹣a＝a，
∴a＝2，
∴CD＝2，
故答案为：BC＝2EF，CD＝2．
【点睛】
本题考查了全等三角形的判定与性质，菱形的性质，等边三角形的性质，等腰直角三角形的性质等知识，熟练掌握全等三角形的判定与性质，等边三角形，等腰直角三角形的边角关系是解决问题的关键．
1． (2023·河南濮阳·一模）如图，有一张矩形纸条ABCD，AB＝5，,点M，N分别在边AB，CD，CN＝1．现将四边形BCNM沿MN折叠，使点B，C分别落在点， 处，在点M从点A运动到点B的过程中，若边与边CD交于点E，则点E相应运动的路径长___．
【答案】##
【解析】
【分析】
探究点的运动轨迹，寻找特殊位置解决问题即可
【详解】
解：如图
∵四边形是矩形，
，
，
由翻折的性质可知：，
，
，
，
，
如图
当点与重合时，，设，
在中，则有，解得，
，
如图
当点运动到时，的值最大，
，
如图
当点运动到点落在时，
（即），
∴点的运动轨迹，
运动路径：
=．
故答案为：
【点睛】
本题考查翻折变换，矩形的性质，解直角三角形等知识，解题的关键是理解题意确定关键点的位置，灵活运用所学知识解决问题．难点是对点位置的判断．
2． (2023·安徽安庆·九年级开学考试）如图．直线与坐标轴相交于A、B两点，动点P在线段AB上，动点Q在线段OA上、连结OP，且满足，则当______度时，线段OQ的最小值为______．
【答案】 30， 2
【解析】
【分析】
过点O作OE⊥AB于点E，过点Q作QF⊥AB于点F，设OQ=m，PE=n，构造，建立一元二次方程，根据方程有实数根确定的最小值，进而求得∠POQ的度数，即可求得答案．
【详解】
如图，过点O作OE⊥AB于点E，过点Q作QF⊥AB于点F，设OQ=m，PE=n
∵直线与坐标轴相交于A、B两点，
，
，
，
，
，，
，
，
，
，，
，
，
，
在 中, ,
,
在 Rt 中，
，
，
,
整理得, ,
,
,
,
解得, 舍弃 或 ,
的最小值为 2 ,
的最小值为 2 , 此时 ,
,
∴
故答案为：30,2
【点睛】
本题考查相似三角形的判定和性质，一元二次方程的根的判别式等知识，学会添加常用
辅助线，构造相似三角形解决问题是解题的关键．
3． (2023·四川巴中·九年级期末）如图，在矩形ABCD中，对角线AC与BD相交于点O，AB＝3，BC＝4，将△ABO沿着AC折叠得到ΔAB′O，B′O与AD相交于点E，则OE的长是______．
【答案】##
【解析】
【分析】
连接交于点，连接，由折叠可得，，根据矩形性质和勾股定理可得，利用，可得，所以，然后证明△，进而可以解决问题．
【详解】
解：如图，连接交于点，连接，
由折叠可知：，，
在矩形中，
，，，
，
，
，
，
，
，
，，
，，
△，
，
，
，
，
，
．
的长是．
故答案为：．
【点睛】
本题考查了矩形性质，勾股定理，相似三角形的性质和判定，关键主要考查学生的推理和计算能力．
4． (2023·广东·模拟预测）在平面直角坐标系xOy中，已知，，三点，其中，函数的图象分别与线段BC，AC交于点P，Q．若，则t的值为______．
【答案】2
【解析】
【分析】
用t分别表示出S△PAB和S△PQB，然后根据题意得出一元二次方程求解即可．
【详解】
解：如图所示，
∵A（2t，0），C（2t，4t），
∴AC⊥x轴，
当x=2t时，y=，
∴Q（2t，），
∵B（0，﹣2t），C（2t，4t），
设直线BC的解析式为：，将两点代入可得：
，
解得：，
∴直线BC的解析式为：y=3x﹣2t，
则3x﹣2t=，
解得：x1=t，x2=（舍），
∴P（t，t），
∵S△PAB=S△BAC﹣S△APC，S△PQB=S△BAC﹣S△ABQ﹣S△PQC，
∵S△PAB﹣S△PQB=t﹣1，
∴（S△BAC﹣S△APC）﹣（S△BAC﹣S△ABQ﹣S△PQC）=t﹣1，
S△ABQ+S△PQC﹣S△APC=，
解得：t=2，
故答案为：2．
【点睛】
本题考查的知识点是待定系数法求一次函数解析式、反比例函数的图像及其性质以及三角形的面积公式，一元二次方程的应用，解题关键是利用双曲线函数图象解题．
5． (2023年浙江省宁波市中考数学模拟预测数学试题）太极推盘是一种常见的健身器材（如图1），转动两个圆盘便能锻炼身体．取推盘上半径均为0.4米的圆A与圆B（如图2）且AB=1米，圆A绕圆心A以2°每秒的速度逆时针旋转，圆B绕圆心B以2°每秒的速度顺时针旋转．开始转动时圆A上的点C恰好落在线段AB上，圆B上的点D在AB下方且满足∠DBA=60°，则在两圆同时开始转动的30秒内，CD的最小值是_______米．
【答案】0.5##
【解析】
【分析】
连接CD，以AC、CD为邻边构造平行四边形ACDE，过D作AB的平行线MN，求得∠EBA=30°，当AE⊥EB时，CD有最小值，据此即可求解．
【详解】
解：连接CD，以AC、CD为邻边构造平行四边形ACDE，过D作AB的平行线MN，
设∠CAB=2t°，由题意得∠ABD=60°-2t°，
∴∠MDE=∠CAB=2t°，∠BDM=180°- ∠ABD=120°+2t°，
∴∠BDE=120°+2t°+2t°=120°+4t°，
又DE=AC=DB，
∴∠EBD=∠BED==30°-2t°，
∴∠EBA=30°，
∴当AE⊥EB时，CDmin=AEmin=AB÷2=0.5(米)．
故答案为：0.5．
【点睛】
本题考查了圆的基本概念，平行四边形的判定和性质，含30度角的直角三角形的性质，等腰三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．