
江苏省南京市钟英中学2023—2024学年+八年级下学期3月月考数学试卷
展开一、选择题(本大题共6小题,每小题2分,共12分. 在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
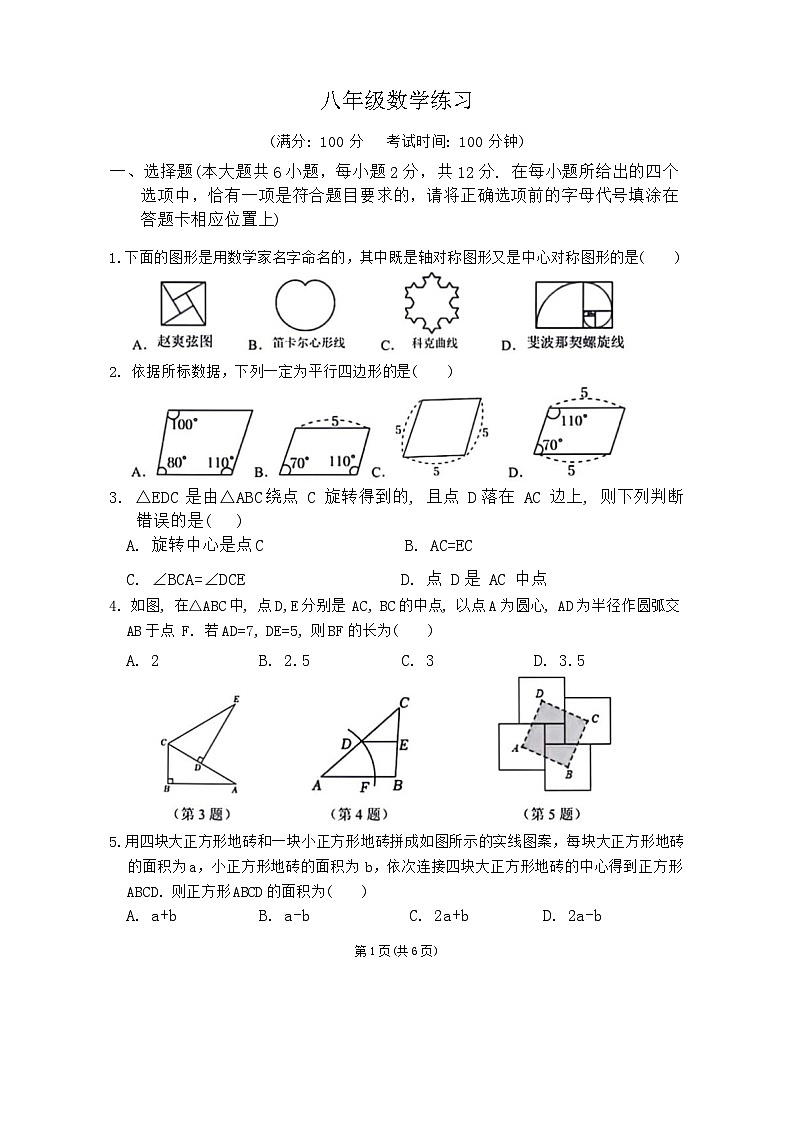
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
2. 依据所标数据,下列一定为平行四边形的是( )
3. △EDC 是由△ABC绕点 C 旋转得到的, 且点 D落在 AC 边上, 则下列判断错误的是( )
A. 旋转中心是点C B. AC=EC
C. ∠BCA=∠DCE D. 点 D是 AC 中点
4. 如图, 在△ABC中, 点D,E分别是 AC, BC的中点, 以点A为圆心, AD为半径作圆弧交AB于点 F. 若AD=7, DE=5, 则BF的长为( )
A. 2 B. 2.5 C. 3 D. 3.5
5.用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖的面积为a,小正方形地砖的面积为 b,依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为( )
A. a+b B. a-b C. 2a+b D. 2a-b
第1页(共6页)6.如图, 在正方形ABCD 中, E、F分别是AB、BC的中点, CE交 DF于点 G, 连接 AG. 下列结论: ①CE=DF; ②CE⊥DF;③∠EAG=30° : ④∠AGE=∠CDF. 其中正确的是( )
A. ①② B. ①③ C. ①②④ D. ①②③
二、填空题(本大题共10小题,每小题2分,共20分. 不需写出解答过程,请把答案直接填写在答题卷相应位置上)
7. 在矩形ABCD中, AC、 BD相交于点O, 若∠OAB=65° , 则∠BOC= ° .
8.如图,两条宽都为 3的纸条交叉成60°角重叠在一起,则重叠四边形的面积为 .
9. 在平面直角坐标系中, 平行四边形OABC的顶点 A、 C的坐标分别是(6, 1)、 (2,4),则点B的坐标是 .
10. 已知菱形的周长是 52cm, 一条对角线长是24cm, 则它的面积是 cm².
11.如图,在平行四边形ABCD中,AE平分∠DAB,∠AED=26° ,则∠C的度数为 .
12. 如图, 在 Rt△ABC中, ∠BAC=90° , AD是△ABC的中线, 点E, F 分别是 AD, AC的中点, 连接EF, 若 EF=3, 则AD的长为 .
13.中国古代数学家刘徽给出了证明三角形面积公式的出入相补法. 如图,在△ABC中,分别取AB、AC的中点D、E, 连接DE, 过点A 作 AF⊥DE, 垂足为 F, 将△ABC 分割后拼接成矩形 BCHG. 若 DE=3, AF=2, 则△ABC的面积是 .
14.如图,在菱形 ABCD中, 对角线AC, BD相交于点O,点E 在 AD上, 连接 EO 并延长,交 BC于点 F. 若AB=5, OE=2, 则四边形CDEF 的周长是 .
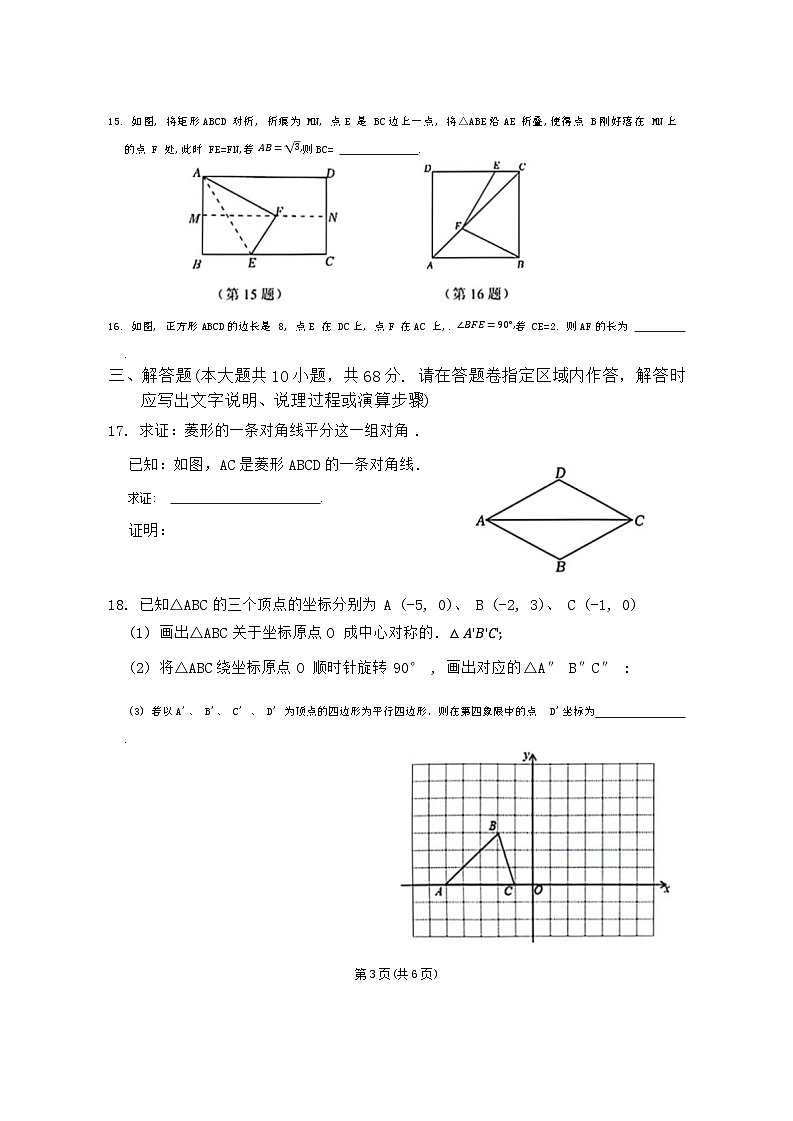
第2页(共6页)15. 如图, 将矩形ABCD 对折, 折痕为 MN, 点E 是 BC边上一点, 将△ABE沿AE 折叠,使得点 B刚好落在 MN上的点 F 处,此时 FE=FN,若 AB=3,则BC= .
16. 如图, 正方形ABCD的边长是 8, 点E 在 DC上, 点F 在AC 上,. ∠BFE=90°,若 CE=2. 则AF的长为 .
三、解答题(本大题共10小题,共68分. 请在答题卷指定区域内作答,解答时应写出文字说明、说理过程或演算步骤)
17. 求证:菱形的一条对角线平分这一组对角.
已知:如图,AC是菱形ABCD的一条对角线.
求证: .
证明:
18. 已知△ABC的三个顶点的坐标分别为A (-5, 0)、 B (-2, 3)、 C (-1, 0)
(1) 画出△ABC关于坐标原点O 成中心对称的. △A'B'C';
(2) 将△ABC绕坐标原点O 顺时针旋转90° , 画出对应的△A″ B″C″ :
(3) 若以A'、 B'、 C' 、 D' 为顶点的四边形为平行四边形,则在第四象限中的点 D'坐标为 .
第3页(共6页)19. 如图, 在 ⊙ABCD中, E, F 位于BC, AD 上, AE, CF 分别平分. ∠BAC,∠DCA.
(1) 求证: 四边形 AECF 是平行四边形;
(2) 当 △ABC满足条件 时,四边形AECF是矩形.
20. 如图, E, F, G, H 是四边形ABCD 各边的中点.
(1) 证明: 四边形 EFGH为平行四边形.
(2) 若四边形 ABCD 是矩形, 且其面积是 7cm², 则四 边 形 EFGH 的面 积是 cm².
21. 如图, 在四边形ABCD中, 点E, F分别在边 BC, CD上, 连接AE, AF, 已知 △ABE ⊆△ADF.
(1) 若 AD∥BC, 求证: 四边形ABCD 是菱形;
(2)以下条件: ①∠BAD=∠BCD; ②AB=CD;③BC=CD. 如果用其中的一个替换
(1) 中的“AD∥BC”,也可以证明四边形ABCD 是菱形,那么可以选择的条件是 .(填写满足要求的所有条件的序号).
第4页(共6页)22. 如图, 矩形 EFGH的顶点 E、 G 分别在菱形ABCD的边AD、BC上, 顶点 F、 H 在菱形ABCD的对角线BD上.
(1) 求证: BG=DE;
(2) 若E为AD的中点, AB=5. 则FH的长 .
23.如图, 在正方形ABCD 中,点E、F、G 分别在CD、AD、BC上, FG⊥BE, 垂足为O.
(1) 求证: BE=FG:
(2) 若 O是 BE 的中点, 且BC=8, EC=3, 则AF的长 ..
24. 如图, 在 △ABC中, AE 平分 ∠BAC,BE⊥AE于点E, 点 F 是 BC的中点.
(1) 如图1, BE 的延长线与AC 边相交于点 D, 求证: EF=12AC-AB;
(2) 如图 2, 探究线段 AB、 AC、 EF 之间的数量 关系, 直接写出你的结论: .
25. 如图, 点O 是∠MAN内一点, 求作线段PQ, 使 P、Q分别在射线AM、AN上,且点O 是 PQ的中点.
要求:(1) 用直尺和圆规作图,保留作图痕迹;
(2) 用两种不同的方法.
26. 如图①, 正方形ABCD 中, 点 E 是对角线 AC上任意一点, 过点 E 作 EF⊥AC, 垂足为E,交 BC所在直线于点 F. 探索 AF 与DE 之间的数量关系,并说明理由.
小明在解决这一问题之前,先进行特殊思考:如图②,当E是对角线AC的中点时, 他发现AF与DE之间的数量关系是 . 若点 E 在其它位置时, 这个结论是否都成立呢?小明继续探究,他用“平移法”将AF沿AD方向平移得到DG,将原来分散的两条线段集中到同一个三角形中,如图③,这样就可以将问题转化为探究DG 与DE 之间的数量关系.
(1) 请你按照小明的思路,完成解题过程;
(2) 你能用与小明不同的方法来解决李老师给出的“数学问题”吗? 请写出解题过程.
第6页(共 6页)
江苏省南京市钟英中学2023—2024学年+八年级下学期3月月考数学试卷: 这是一份江苏省南京市钟英中学2023—2024学年+八年级下学期3月月考数学试卷,共6页。
江苏省南京市钟英中学2023—2024学年+八年级下学期3月月考数学试卷: 这是一份江苏省南京市钟英中学2023—2024学年+八年级下学期3月月考数学试卷,共6页。
2023-2024学年江苏省南京市钟英中学八年级(上)10月月考数学试卷(含解析): 这是一份2023-2024学年江苏省南京市钟英中学八年级(上)10月月考数学试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












