江苏省苏州市高新区第一初级中学校2023-2024学年九年级下学期3月月考数学试卷+

这是一份江苏省苏州市高新区第一初级中学校2023-2024学年九年级下学期3月月考数学试卷+，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

命题人：黄静 王亚平 审核人：唐丽
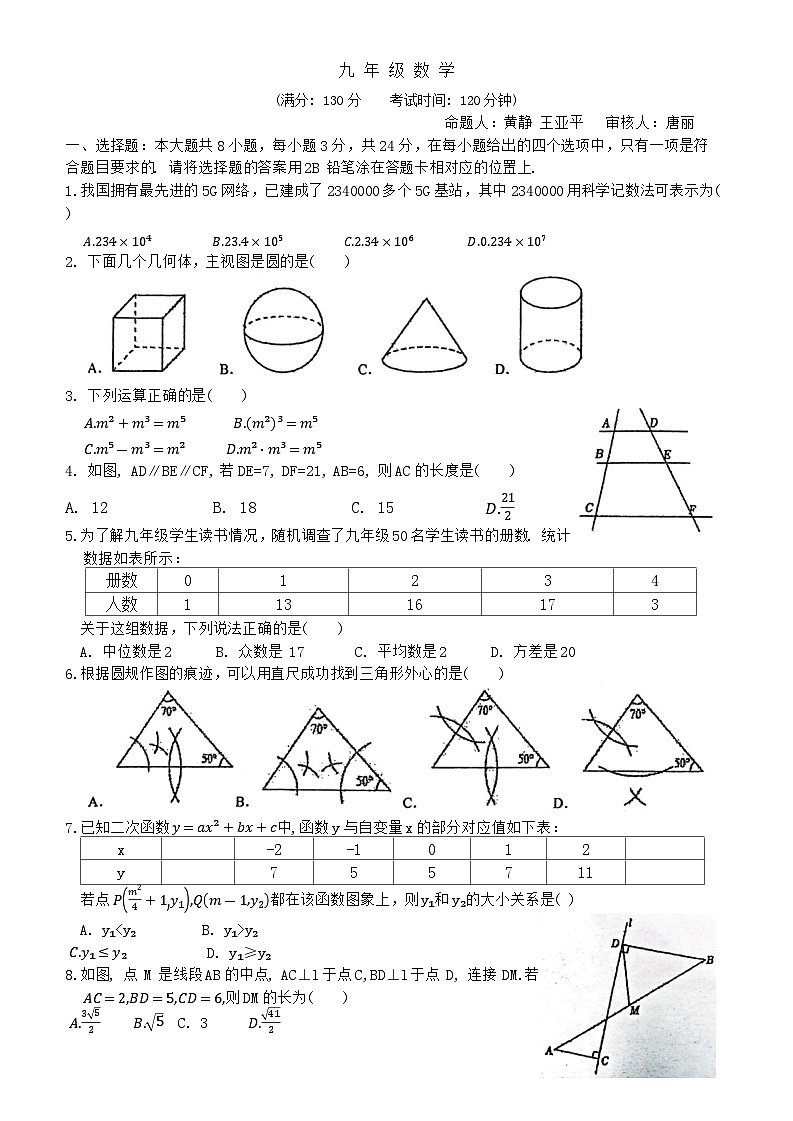
一、选择题：本大题共8小题，每小题3分，共24分，在每小题给出的四个选项中，只有一项是符合题目要求的. 请将选择题的答案用2B 铅笔涂在答题卡相对应的位置上.
1.我国拥有最先进的5G网络，已建成了2340000多个5G基站，其中2340000用科学记数法可表示为( )
A.234×10⁴ B.23.4×10⁵ ×10⁶ ×10⁷
2. 下面几个几何体，主视图是圆的是( )
3. 下列运算正确的是( )
A.m²+m³=m⁵ B.m²³=m⁵
C.m⁵-m³=m² D.m²⋅m³=m⁵
4. 如图, AD∥BE∥CF, 若DE=7, DF=21, AB=6, 则AC的长度是( )
A. 12 B. 18 C. 15 D.212
5.为了解九年级学生读书情况，随机调查了九年级50名学生读书的册数. 统计数据如表所示：
关于这组数据，下列说法正确的是( )
A. 中位数是2 B. 众数是 17 C. 平均数是2 D. 方差是20
6.根据圆规作图的痕迹，可以用直尺成功找到三角形外心的是( )
7.已知二次函数 y=ax²+bx+c中,函数y与自变量x的部分对应值如下表：
若点 Pm24+1y1,Qm-1y2都在该函数图象上，则y₁和y₂的大小关系是( )
A. y₁y₂
C.y₁≤y₂ D. y₁≥y₂
8.如图, 点 M 是线段AB的中点, AC⊥l于点C,BD⊥l于点 D, 连接 DM.若 AC=2,BD=5,CD=6,则DM的长为( )
A.352 B.5 C. 3 D.412
1册数
0
1
2
3
4
人数
1
13
16
17
3
x

-2
-1
0
1
2

y

7
5
5
7
11

二、填空题：本大题共8小题，每小题3 分，共24分. 把答案直接填在答题卡相对应的位置上.
9. 若代数式 x+3有意义，则实数x的取值范围是 .
10. 如图，飞镖游戏板由含大小相等的等腰直角三角形格子构成，小东向游戏板随机投掷一枚飞镖，击中黑色区域的概率是 .
11. 因式分解: x³-4x=.
12.图1 是伸缩折叠不锈钢晾衣架的实物图，图2 是它的侧面示意图，AD与CB 相交于点O, AB∥CD,根据图2中的数据可得x的值为 .
13.如图, 扇形AOB 的半径OB=2, 将扇形AOB绕点 A逆时针旋转得扇形 ACD, 当点C落在 AB上时旋转停止，则扇形ACD中空白部分的面积为 ( 结果保留π).
14.代数式mx-n的值随x取值的变化而变化，如表是当x取不同值时对应的整式的值：
则关于x的方程-mx+n=3的解为x= .
15.如图，4个小正方形拼成“L”型模具，其中三个顶点在正坐标轴上，顶点D在反比例函数 y=kxk≠0的图象上，若 SABC=4, 则k= .
16. 如图, 四边形ABCD中, ∠ABC=90°, AB=BC, BD平分∠ADC, 连结AC, 若AD=1, AD三、解答题：本大题共11 小题，共82分. 把解答过程写在答题卡相对应的位置上，解答时应写出必要的计算过程、推算步骤或文字说明. 作图时用2B铅笔或黑色墨水签字笔.
17. (5分) 计算: 12-2-12+|3-2|. 18.(5分) 解不等式组: 5x-2<3x+12x-23≥x-1
19.(6分) 先化简再求值: x+1-3x-1÷x2+4x+4x-1, 其中x=3.
20.(6分) 如图, 在平行四边形ABCD中, BD是它的一条对角线.
(1) 尺规作图: 作 BD的垂直平分线EF,分别交AD, BC 于点E, F(不写作法，保留作图痕迹)；
(2) 连接 BE, 若∠DBE=20°, 求∠AEB 的度数.
21.(6分) 在庆祝龙年的元旦联欢会上，九年级 1班进行抽奖活动，活动规则如下：将4 张正面标有龙、蛇、马、羊的纸牌(纸牌反面完全相同) 洗匀后，反面朝上放在桌子上，参与者每次随机从中抽取两张纸牌，若抽到“龙”和“马”，即组成“龙马精神”这个寓意美好的成语，则参与者可获得奖品.
(1) 王小虎随机抽出一张纸牌，抽到“龙”牌的概率是 ；
(2) 丽丽决定参加游戏，请用树状图或列表法说明丽丽获得奖品的概率.
2x
-5
-4
-3
-2
-1
0
mx-n
9
6
3
0
-3
-6
22.(8分) 某校根据课程设置要求，开设了数学类拓展性课程，为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查(每人必须且只选其中一项)，并将统计结果绘制成如下统计图(不完整). 根据统计图提供的信息，解答
下列问题：
(1) m= , n= ;
(2) 在扇形统计图中,“C. 实验探究”所对应的扇形的圆心角度数是 度；
(3) 请根据以上信息补全条形统计图：
(4)该校共有 1600名学生,试估计全校最喜欢“思想方法”的学生人数.
23.(8分) 用充电器给某手机充电时，其屏幕画面显示目前电量为20%(如图1). 经测试，在用快速充电器和普通充电器对该手机充电时，其电量y(单位：%) 与充电时间x(单位：h)的函数图象分别为图2中的线段AB，AC. 根据以上信息， 回答下列问题：(1) 求线段AC对应的函数表达式；
(2)先用普通充电器充电 ah后，再改为快速充电器充满电，一共用时3h，请在图2中画出电量y(单位：%) 与充电时间x(单位：h) 的函数图象，并标注出a所对应的值.
24.(8分) 有一种可折叠台灯，它放置在水平桌面上，图1是台灯的平面示意图，其中点B，E，D均可转动，现测得AB=BE=ED=CD=18cm，经多次调试发现当点B，E都在灯座 CD的垂直平分线上时(如图2所示) 放置最平稳.
(1) 求放置最平稳时灯座CD与灯杆ED的夹角的大小；
(2)当A 点到水平桌面(CD所在直线)的距离为42cm-43cm时，台灯光线最佳，能更好的保护视力.若台灯放置最平稳时，将∠ABE调节到105°，试通过计算说明此时光线是否最佳.(参考数据： sin15° ≈0.26,cs15∘≈0.97,tan15∘≈0.27,3≈1.73)
325.(10分) 如图, ⊙O是△ABC的外接圆, AB是⊙O的直径, ∠DCA=∠B.
(1) 求证: CD是⊙O的切线;
(2) 若DE⊥AB, 垂足为E, DE交 AC于点F, CD=15,tanA=34,求CF的长.
26.(10分) 李老师让同学们以“旋转”为主题展开探究.
【问题情境】
如图1, 在矩形ABCD中, AB=4, AD=6. 将边 AB 绕点 A逆时针旋转(0° <θ<180° ) 得到线段AE, 过点E作EF⊥AE 交直线 BC与点F.
【猜想证明】
(1) 当θ=90°时, 四边形ABFE的形状为 ;(直接写出答案)
(2) 如图2,当θ=45°时, 连接DE, 求此时△ADE 的面积;
【能力提升】
(3)在【问题情境】的条件下，是否存在θ，使点F，E，D三点共线. 若存在，请求出此时 BF 的长度； 若不存在，请说明理由.
27.(10分) 我们将抛物线 y=ax²+bx+c(a≠0,b≠0且a≠b) 与抛物线 y=bx²+cx+a称之为“轮换抛物线”. 例如：抛物线 y=3x²+4x+5与抛物线 y=4x²+5x+3就是一组轮换抛物线. 已知抛物线 C₁:y= ax²+bx+4a-3,其轮换抛物线记作C₂.
(1) 若 C₁与C₂交于y轴上的同一点 M, 求a的值;
(2) 在(1) 的条件下且b<0，抛物线C₁与其轮换抛物线 C₂的另一个交点记作 N点，若将点M绕点N顺时针旋转 90°后，M的对应点 P 恰好落在抛物线C₁的图象上，求出此时b的值；
(3) 小明同学阅读了《苏科版(数学)》课本九年级下册 18-19页《数学实验室》介绍的用几何画板画二次函数图象内容后，自己动手画了抛物线 C₁:y=ax²+bx+4a-3及其轮换抛物线 C₂的图象， C₁与 C₂与y轴的交点分别记作P、Q(P、Q两点不重合). 小明发现，不论a、b为何值时，两抛物线始终有一交点 G 点在与x轴垂直的某一固定直线上运动. 若 PG=QG,记 S=ab,求S的最大值.
4