河南省安阳市文峰区安阳正一中学2023-2024学年九年级下学期3月月考数学试题

这是一份河南省安阳市文峰区安阳正一中学2023-2024学年九年级下学期3月月考数学试题，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题（每题3分，本题共30分）
1．北京冬奥会和冬残奥会组委会收到来自全球的会徽设计方案，其中很多设计方案体现了对称之美．以下4幅设计方案中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
2．如图，正方体的展开图中相对面数字之和相等，则=（ ）
A．－9B．9C．－6D．－8
3．已知关于的一元二次方程的两实数根分别为，，则的值为（ ）
A．－1B．1C．5D．－5
4．恼人的新冠病毒．有一个人感染了病毒，经过两轮传染，一共有144个人感染，则每轮传染中，平均一个人传染了（ ）个人
A．13B．12C．11D．10
5．圆锥底面圆半径为3cm，高为4cm，则它侧面展开图的面积是（ ）
A．B．C．D．
6．半径为2的圆的内接正六边形的面积是（ ）
A．B．C．D．
7．关于二次函数，下列说法错误的是（ ）
A．图象的开口方向向上
B．函数的最小值为－3
C．当时，随的增大而减小
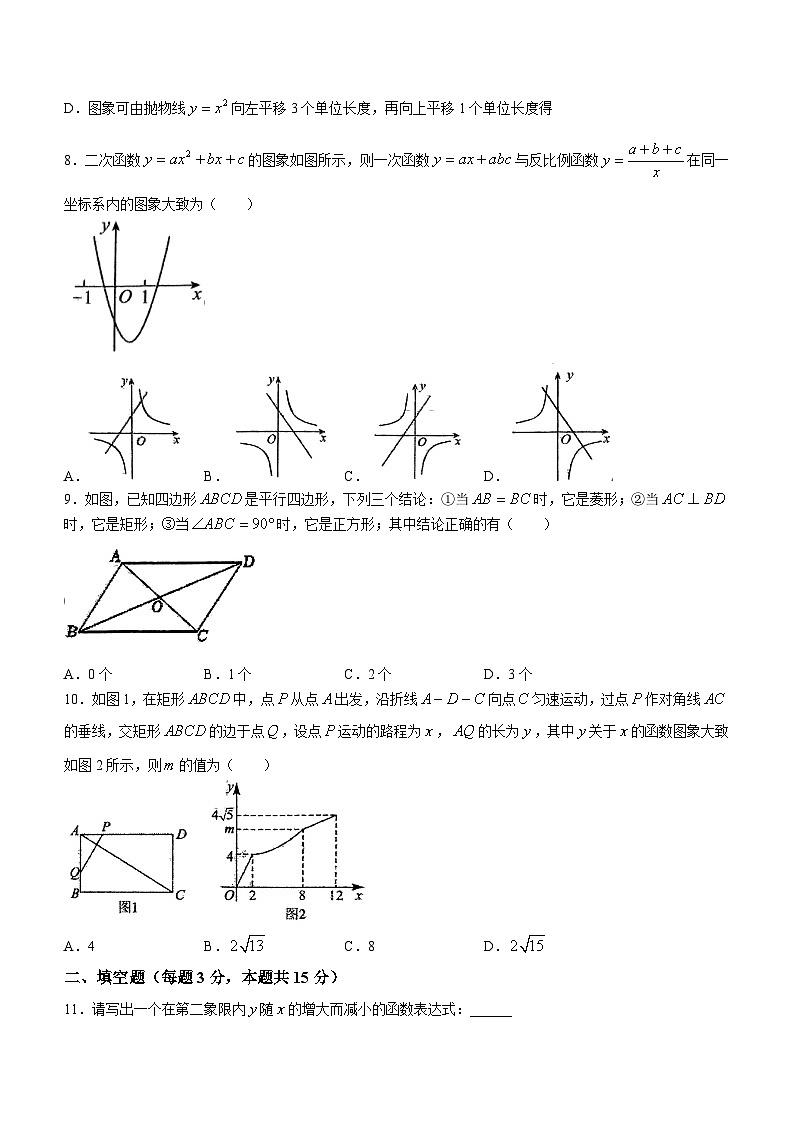
D．图象可由抛物线向左平移3个单位长度，再向上平移1个单位长度得
8．二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）
A．B．C．D．
9．如图，已知四边形是平行四边形，下列三个结论：①当时，它是菱形；②当时，它是矩形；③当时，它是正方形；其中结论正确的有（ ）
A．0个B．1个C．2个D．3个
10．如图1，在矩形中，点从点出发，沿折线向点匀速运动，过点作对角线的垂线，交矩形的边于点，设点运动的路程为，的长为，其中关于的函数图象大致如图2所示，则的值为（ ）
A．4B．C．8D．
二、填空题（每题3分，本题共15分）
11．请写出一个在第二象限内随的增大而减小的函数表达式：______
12．现有四张完全相同的卡片，上面分别标有数字－1，－2，3，4．把卡片背面朝上洗匀，然后从中随机抽取两张，则这两张卡片上的数字之积为负数的概率是______．
13．不等式组的最大整数解为______．
14．如图所示的网格中，每个小正方形的边长为1，点，，均为小正方形的顶点，且点在上，则阴影部分的面积为______．
15．如图，菱形的边长为5，对角线为8，以顶点为圆心，2为半径画圆，点在对角线上运动，当射线与圆相切时，的长是______．
三、解答题（本大题共75分）
16．（10分）（1）计算：（2）．
17．（9分）某初级中学为了解学生平均每天完成课后作业用时情况，从本校学生中随机抽取300名进行问卷调查，并将调查结果进行了整理，结果如下，
调查问卷1．近两周你平均每天完成课后作业用时约______分钟．如果你平均每天完成课后作业用时超过90分钟，请回答第2个问题．
2．影响你完成课后作业用时的主要原因是______．（单选）
A．作业难度大B．作业题量大C．自身写作业效率低D．其他
学生平均每天完成课后作业用时频数分布表
根据以上信息，解答下列问题：影响学生完成课后作业用时的主要原因统计图
（1）本次调查中，学生平均每天完成课后作业用时的中位数落在______这一组．
（2）若该校共有学生1000人，请估计有多少人未能在90分钟内完成课后作业．
（3）请对该校学生完成课后作业用时情况作出评价，并提出两条合理化建议
18．（9分）一次函数与函数为的图象交于，两点．
（1）求这两个函数的解析式；
（2）根据图象，直接写出满足时，的取值范围；
19．（9分）“端午节”吃粽子是中国传统习俗，在“端午节”来临前，某超市购进一种品牌粽子，每盒进价是40元，根据以往销售经验发现，当每盒售价定为50元时，日销售量为500盒，每盒售价每提高1元，日销售量减少10盒，设每盒售价为元，日销售量为盒，
（1）直接写出销售量与售价的函数关系式：______；
（2）当每盒售价定为多少元时，日销售利润（元）最大?最大利润是多少
20．（9分）安阳红旗渠机场于2023年11月29日正式通航，很多市民共同见证了这一历史时刻．如图，市民甲在处看见飞机的仰角为45°，同时另一市民乙在斜坡上的处看见飞机的仰角为30°，若斜坡的坡比=1：5，，铅垂高度，米（点、、、在同一水平线上）．
求飞机距离地面的高度．（结果保留根号）
21．（9分）．如图是直径，是⊙O上异于，的一点，点是DC延长线上一点，连接，，，且。
（1）求证：直线是的切线；
（2）若，，求的值；
22．（10分）跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点为飞行距离计分的参照点，落地点超过点越远，飞行距离分越高，2022年北京冬奥会跳台滑雪标准台的起跳台的高度为66米，基准点到起跳台的水平距离为75米，高度为h米（h为定值）．设运动员从起跳点起跳后的高度与水平距离之间的函数关系为．
（1）的值为______；
（2）若运动员落地点恰好到达点，且此时，，求基准点的高度h；（3）若时，运动员落地点要超过点，直接写出的取值范围．
23．（10分）特殊发现
（1）如图1，正方形与正方形的顶点重合，，分别在，边上，连接，则有：
①=______；②直线与直线所夹的锐角等于______度；
（2）理解运用
将图1中的正方形绕点逆时针旋转，连接、．
①如图2，（1）中的结论是否仍然成立?请说明理由；
②如图3，若、、三点在同一直线上，且过边的中点，，请直接写出的长；
安阳正一中学2023—2024学年下学期第六次阶段考
九年级数学参考答案
1．C2．B3．B4．C5．D6．C7．D8．C9．B
10．B解：由点可得：当时，则，
结合图象可得：，当时，，重合，当时，，重合，∴，而，∴，如图，当时，，重合，记，的交点为，则，∴，∴，，此时，∴，，
∴，即，
11．（答案不唯一）12．．13．314．
15．或
解：连接交于，设射线与圆相切时的切点为，连接，如图；∵四边形是菱形，
∴，，，，
∴，∴，
∵，，
∴；∵，∴，
∵，∴，∴，即，
∴；当在圆的左边与圆相切时，由对称性知，，
则；综上，的长为或；
16．（1）（2）原式=
17．（1）
（2）解：（人）．答：估计有160人未能在90分钟内完成课后作业．
（3）解：评价：约的学生平均每天完成课后作业的时间超过90分钟．
建议：①减少作业题量；②根据学生的能力分布布置作业．
18．（1）解：将代入，可得，解得，
反比例函数解析式为；在图象上，
，，
将，代入，得：，解得，
一次函数解析式为；
（2）解：，
19．（1）解：
（2）由题意得，
，
∵，开口向下∴时，最大，最大值为9000，
∴当每盒售价定为70元时，日销售利润（元）最大，最大利润是9000元．
20．解：∵斜坡的坡比=1：3，铅垂高度米，∴，∴米，
过点作于，则四边形是矩形，∴米，，
∵，，∴是等腰直角三角形∴，
设米，则米，
米，
在中，，
∴，
解得，∴米
答：飞机距离地面的高度为．
21．（1）解：如图所示，连接，
∵是直径，∴，
∴，
又∵，∴，
∵，∴，
∴，即，∴，
又∵为半径，∴直线是的切线；
（2）解：∵，，∴，∴，
，则，，
在中，，
在中，，即；
22．（1）解：；
（2）解：∵，，∴，
∵基准点K到起跳台的水平距离为75m，∴，
∴基准点K的高度h为21m；
（3）∵，∴，∵运动员落地点要超过点，
∴当时，，即，解得，故答案为：；
23．（1）解：①，②直线和直线所夹的锐角等于45°，
（2）①（1）中的结论仍然成立，
理由如下：连接，，如图，
∵四边形和四边形为正方形，
∴，，
∴和为等腰直角三角形，
∴，，，∴，，
∴，∴；延长，交于点，交于点，
∵，∴，∵，
∴，∴，
即直线与直线所夹的锐角等于45°，∴（1）中的结论仍然成立；
②如图，连接，∵四边形是正方形，∴，∵，
∴，∵边的中点为，∴，
∴在和中，，
∴，∴，
∴，
∴；故答案为：．
平均每天完成课后作业用时（分钟）
人数
15
44
57
136
48