
浙教版七年级数学下册基础知识专项讲练 专题3.32 整式的乘除(几何图形问题50题)(基础篇)(专项练习)
展开一、单选题
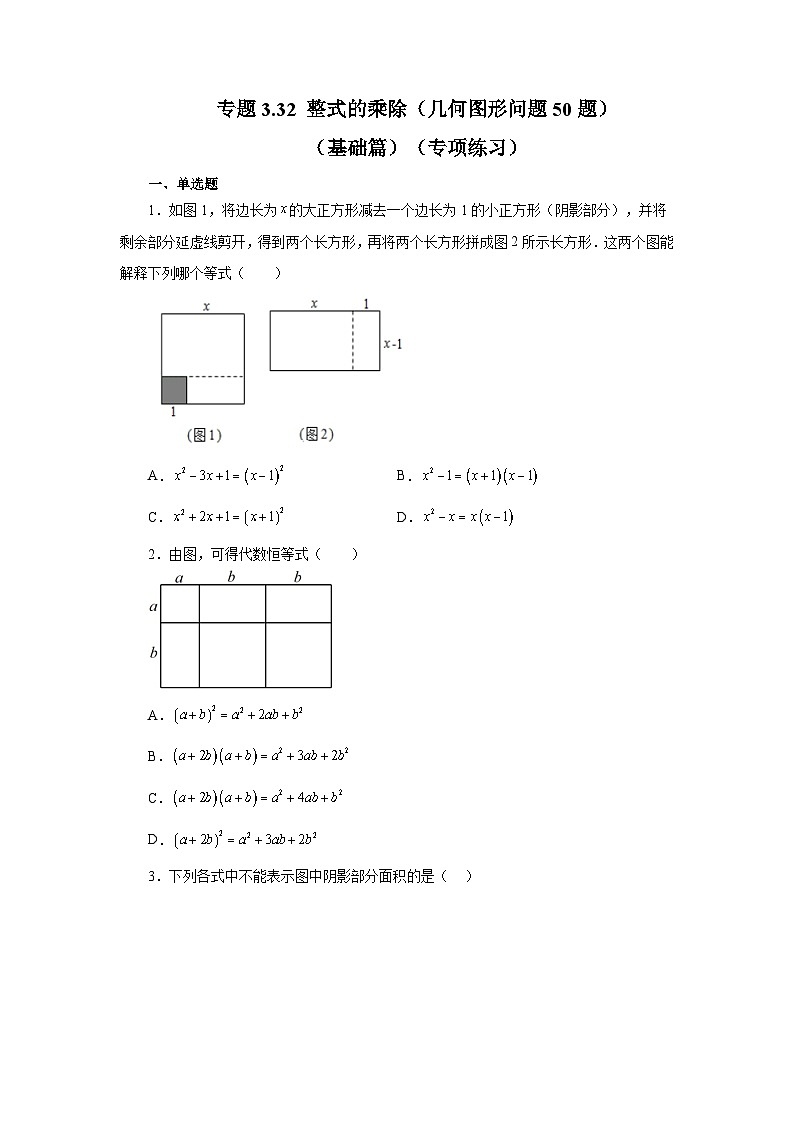
1.如图1,将边长为的大正方形减去一个边长为1的小正方形(阴影部分),并将剩余部分延虚线剪开,得到两个长方形,再将两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A.B.
C.D.
2.由图,可得代数恒等式( )
A.
B.
C.
D.
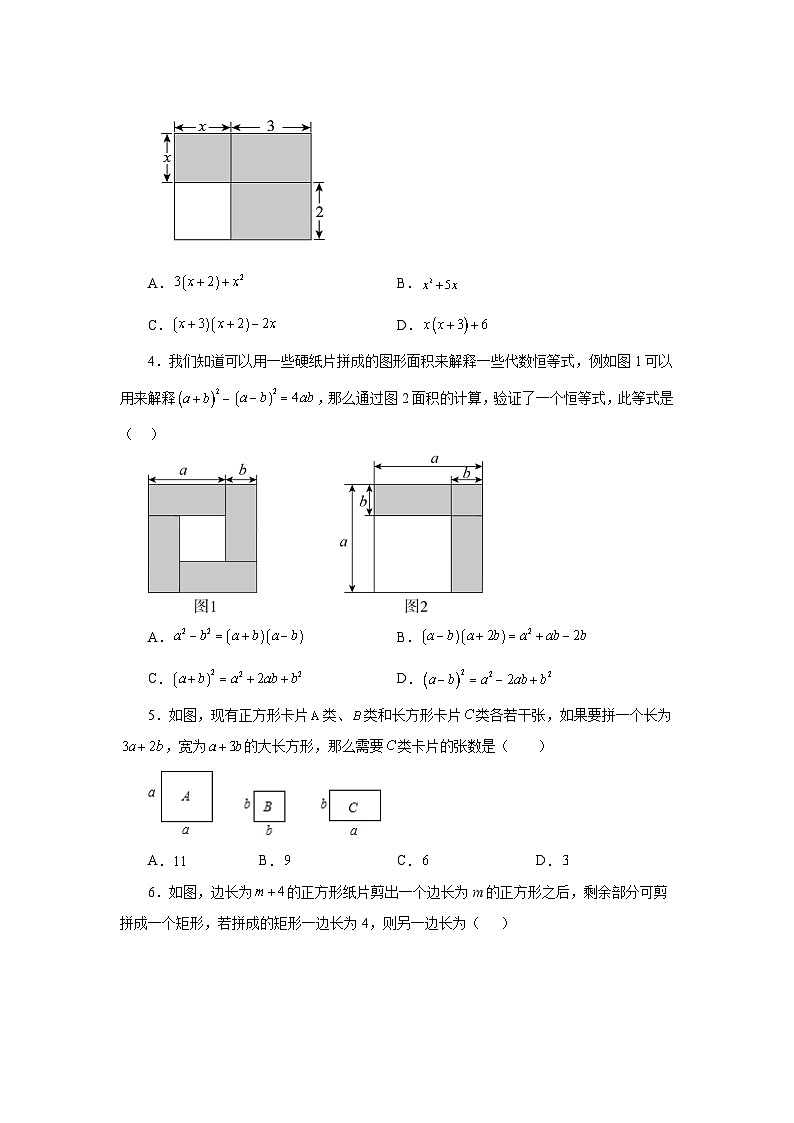
3.下列各式中不能表示图中阴影部分面积的是( )
A.B.
C.D.
4.我们知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式,例如图1可以用来解释,那么通过图2面积的计算,验证了一个恒等式,此等式是( )
A.B.
C.D.
5.如图,现有正方形卡片类、类和长方形卡片类各若干张,如果要拼一个长为,宽为的大长方形,那么需要类卡片的张数是( )
A.B.C.D.
6.如图,边长为的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为( )
A.B.C.D.
7.如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )
A.B.
C.D.
8.将一个长方形按如图①所示进行分割,得到两个完全相同的梯形,再将它们拼成如图②所示的图形,根据两个图形中面积间的关系,可以验证的乘法公式为( )
A.B.
C.D.
9.在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A. B.
C. D.
10.如图1,边长为a的正方形是由边长为b的正方形和四个全等的四边形组成的,沿正方形内的虚线将四个全等的四边形剪下,拼成如图2所示的四边形,通过计算四边形的面积,可以验证的乘法公式是( )
A.B.
C.D.
11.如图所示的分割正方形拼接成长方形的方案中,可以验证( )
A.B.
C.D.
12.如图,图1中的阴影部分移动成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )
A.B.
C.D.
13.4张长为a,宽为的长方形纸片,按如图的方式拼成一个边长为的正方形,图中空白部分的面积为,阴影部分的面积为,若,则a,b满足的关系式是( )
A.B.C.D.
14.如图,大正方形的边长为a,小正方形的边长为b,若用x,y表示四个长方形的两边长(),观察图案及以下关系式:①;②;③;④;⑤ ;其中正确的关系式有 ( )
A.①②③④B.①②③⑤C.①②④⑤D.①③④⑤
15.如图,两正方形并排在一起,左边大正方形边长为右边小正方形边长为,则图中阴影部分的面积可表示为( ).
A.B.
C.D.
二、填空题
16.如图(图中长度单位:,阴影部分的面积是___________.
17.三个长方形纸片如图1所示无缝隙地拼接在一起,它们的边长分别标记在图1中.现将拼接后的纸片用图2所示方式重新分割成三个长方形A,B,C.根据图2与图1的关系写出一个等式:__________(用含a,b,c,d,e,f的式子表示).
18.如图,某幼儿园要在长方形操场上铺设塑胶地垫(地垫无缝拼接.不可剪裁).现有正方形地垫和长方形地垫若干张.已知操场长宽分别为和则需要用到地垫的张数为___________.
19.在华师大版八年级上册51页的《综合与实践》中,我们学习了代数恒等式可以用硬纸片拼成的图形面积来解释.请结合图形,完成下面的实践与探索活动.
有足够多的长方形和正方形的卡片,如图:
如果选取1号,2号,3号卡片分别为1张,2张,3张,可拼成一个长方形(不重叠无缝隙),如下图,运用拼图前后面积之间的关系写出算式:__________.
或
20.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为,宽为的大长方形,则需要___________张C类卡片.
21.下图中的四边形均为长方形,根据图形的面积关系,写出一个正确的等式:_____________________.
22.如图,正方形ABCD是由正方形EFGH和四个形状、大小一样的直角三角形组成.若阴影部分的面积等于的面积,则阴影部分与正方形ABCD的面积比值为___________.
23.如图,在边长为a的正方形的右下角,剪去一个边长为b的小正方形(),将余下部分拼成一个平行四边形,这一过程可以验证一个关于a,b的等式为______.
24.如图,图为边长为的大正方形中有一个边长为的小正方形,图是由图中阴影部分拼成的一个长方形.
(1)以上两个图形反映了等式:______;
(2)运用(1)中的等式,计算______.
25.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形,分别计算这两个图形的阴影部分的面积,验证了公式_______.
26.如图,大正方形的边长为a,小正方形的边长为b,点E在上,大正方形与小正方形的面积差为60,则阴影部分的面积为________.
27.如图,从边长为a的大正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,这个操作过程能验证的等式是________.
28.某工人师傅要制作一个底面为正方形的无盖长方体盒子,他在一块边长为a的正方形铁皮的四个角,各剪去一个边长为b(),如图所示,若,,则剩余部分的面积是______.
29.如图,阴影部分是边长是的大正方形剪去一个边长是的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列4幅图割拼方法中,其中能够验证平方差公式的有___________(填序号)
30.如图,点D、C、H、G分别在长方形ABJI的边上,点E、F在CD上,若正方形ABCD的面积等于15,图中阴影部分的面积总和为6,则正方形EFGH的面积等于___________.
三、解答题
31.如图,要设计一幅长为厘米,宽为厘米的长方形图案,其中两横两竖涂上阴影,阴影部分的宽均为x厘米.
(1) 阴影部分的面积是多少平方厘米?
(2) 空白区域的面积是多少平方厘米?
32.如图,大正方形边长为,小正方形边长为.
(1) 用含,的式子表示阴影部分的面积;
(2) 若,求阴影部分面积.
33.如图周长为的长方形把长截去剩下的面积比宽截去剩下的面积多,求原长方形的面积.
34.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2),解答下列问题:
(1) 设图1中阴影部分的面积为,图2中阴影部分的面积为,请用含a,b的式子表示:=______,=______;(不必化简)
(2) 由(1)中的结果可以验证的乘法公式是______;
(3) 利用(2)中得到的公式,计算:.
35.如图,将边长为的正方形纸板,沿虚线剪成两个正方形和两个长方形纸板,拿掉边长为的大正方形纸板后,将剩下的三个纸板拼成一个新的长方形纸板.
(1) 求拼成的新的长方形纸板的周长;(用含或的代数式表示)
(2) 当,时,直接写出拼成的新的长方形纸板的面积为___________.
36.探究活动:
(1) 如图①,可以求出阴影部分的面积是 .(写成两数平方差的形式)
(2) 如图②,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 .(写成多项式乘法的形式)
(3) 比较图①、图②阴影部分的面积,可以得到公式 .
37.如图(1)所示,边长为a的正方形中有一个边长为的小正方形,如图(2)所示是由图(1)中的阴影部分拼成的一个长方形.
设图(1)中阴影部分的面积为,图(2)中阴影部分的面积为,请直接用含a,b的式子表示______;______;写出上述过程所揭示的等式:______(用a,b表示)
直接应用:利用这个等式计算:
①;
②;
拓展应用:试利用这个公式求下面代数式的结果:
.
38.如图①,在边长为a的正方形纸片的一角剪去一个边长为b的小正方形.
填空:图①中剩余的L型纸片的面积是_________________;
小明尝试着利用分割法求剩余部分的面积,经过思考得到图②和图③,请你帮助小明求出两种分割图形的面积;
请利用同一个图形面积相等写出两个代数恒等式.
39.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些图形的面积.例如,由图1,可得等式:.
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?,请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知,,求的值.
40.图①是一个长为,宽为的长方形,沿图中虚线用剪刀把它平均分成四个小长方形,然后按图②的形状拼成一个正方形(不重叠,无遮挡).
(1) 图②中的阴影部分的面积为________;
(2) 观察图②,可得三个代数式,,之间的等量关系是________;
(3) 若,,求的值;
(4) 观察图③,利用得到的代数等式的启发,试画出一个几何图形,使它的面积能表示.
41.如图,某市有一块长,宽的长方形地块,规划部门计划将阴影部分进行绿化,在中间正方形空白处修建一个喷水池.
(1) 求绿化的面积;
(2) 当,时,绿化的面积是多少?
42.如图①是一个长为、宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②).
根据上述过程,写出、、之间的等量关系: ;
利用(1)中的结论,若,,则的值是 ;
实际上通过计算图形的面积可以探求相应的等式,如图③,请你写出这个等式: ;
两个正方形,如图④摆放,边长分别为,.若,,求图中阴影部分面积和.
43.如图所示,两个长方形用不同形式拼成图1和图2两个图形.
若图1中的阴影部分面积为;则图2中的阴影部分面积为_________.(用含字母a,b的式子且不同于图1的方式表示)
由(1)你可以得到乘法公式____________.
根据你所得到的乘法公式解决下面的问题:
计算:①;
②.
44.问题背景
如图,图1,图2分别是边长为,a的正方形,由图1易得.
类比探究
类比由图1易得公式的方法,依据图2中的已知条件推导出完全平方的另一个公式.
解决问题
计算:______;
运用完全平方公式计算:;
已知,,求的值.
45.一天,小明和小玲玩纸片拼图游戏,发现利用图中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图可以解释为:.
图可以解释为等式:______ .
在虚线框中用图中的基本图形拼成若干块每种至少用一次拼成一个长方形,使拼出的长方形面积为,并标出此长方形的长和宽.
如图,大正方形的边长为,小正方形的边长为,若用、表示四个长方形的两边长,观察图案,指出以下关系式
;;;其中正确的有几个______
A.个 个 个 个.
46.为了让学生们能更直观地理解乘法公式,李老师上了一节拼图实验课,她用四张长为a,宽为b的小长方形(如图①所示),拼成了一个边长为的正方形(如图②所示),观察图形,回答下列问题:
(1) 图②中,阴影部分的面积是 .
(2) 观察图①②,请你写出三个式子:,,之间的关系: .
(3) 应用:已知,,求值:①;②.
47.在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:
图1 图2
如图1,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且,观察图形,用不同的方法表示这块长方形纸板的面积,可得等式为____________________________;
将图2中边长为a和b的正方形拼在一起,B,C,G三点在同一条直线上,连接和,若这两个正方形的边长满足,,请求出阴影部分的面积.
若图1中每块小长方形的面积为6,四个正方形的面积之和为48,请直接写出图中所有裁剪线(虚线部分)的长度之和.
48.在整式乘法的学习过程中,我们常常利用图形的面积对运算结果加以说明.例如由图①中图形的面积可以得到等式:.
利用图②中图形的面积关系.写出一个正确的等式:___________;
计算的值,并画出几何图形进行说明.
49.(1)请写出三个代数式、和之间数量关系式_______.
(2)如图,线段,C点是AB上的一点,分别以、为边长在的异侧做正方形和正方形,连接;若两个正方形的面积,求阴影部分面积.
50.图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
图2中阴影部分的正方形边长为 ;
观察图2,请你用等式表示,,ab之间的数量关系: ;
根据(2)中的结论,如果x+y=5,xy,求代数式的值.
参考答案
1.B
【分析】根据图形可以用代数式表示出图1和图2的面积,由此得出等量关系即可.
解:由图可知,
图1的面积为:,
图2的面积为:,
所以.
故选:B.
【点拨】本题考查平方差公式的几何背景,解答本题的关键是明确题意,列出相应的代数式.
2.B
【分析】根据大长方形的面积等于3个正方形的面积加上3个长方形的面积即可求解.
解:依题意,得.
故选B.
【点拨】本题考查了多项式乘法与图形的面积,数形结合是解题的关键.
3.B
【分析】用代数式表示各个部分的面积,根据面积之间的和差关系逐项进行判断即可.
解:如图,四边形①的面积为,四边形②的面积为,四边形③的面积为,四边形④的面积为,
四边形①②所拼成的长方形的面积为,
四边形②③所拼成的长方形的面积为,
整个大长方形的面积为,
由各个部分面积之间的关系可得,
A.,正确,故A不符合题意;
B.,错误,故B符合题意;
C.,正确,故C不符合题意;
D.,正确,故D不符合题意;
故选:B.
【点拨】本题考查了多项式乘法的应用,用代数式表示各个部分的面积是正确解答的前提,掌握各个部分面积之间的和差关系是得出正确答案的关键.
4.D
【分析】根据边长乘边长求解正方形面积及用大正方形减阴影部分即可得到答案.
解:由题意可得,
,,
∴,
故选D.
【点拨】本题考查完全平方差公式证明,解题的关键是用不同的求法求空白正方形面积.
5.A
【分析】计算出长为,宽为的大长方形的面积,再分别得出、、卡片的面积,即可看出应当需要各类卡片多少张.
解:长为,宽为的大长方形的面积为:
卡片的面积为:;
卡片的面积为:;
卡片的面积为:;
因此可知,拼成一个长为,宽为的大长方形,
需要块卡片,块卡片和块卡片.
故选:.
【点拨】本题考查了多项式乘法,正确掌握多项式乘多项式运算法则是解题关键.
6.A
【分析】根据大正方形的面积减小正方形的面积矩形的面积,即可解答.
解:根据题意,得:
矩形一边长为,则另一边长为.
故选:A.
【点拨】本题主要考查平方差公式的应用,熟记图形的面积公式是解决此题的关键.
7.D
【分析】分别表示出两个图形的阴影部分的面积,通过面积相等得到等式,即可得出选项.
解:根据图形可知:第一个图形阴影部分的面积为,
第二个图形阴影部分的面积为,
由面积相等可知,,故D正确.
故选:D.
【点拨】本题主要考查了平方差公式的几何背景,解题的关键是阴影部分的面积不变.
8.D
【分析】根据图①与图②的面积相等进行求解即可.
解:由题意得,图①的图形面积为,图②的图形面积为,
∵图①图形与图②图形的面积相等,
∴,
故选D.
【点拨】本题主要考查了平方差公式与几何图形的应用,正确求出两个图形的面积是解题的关键.
9.B
【分析】由图可知,大正方形减小正方形剩下的部分面积为长方形的面积,用两种方法表示出图中阴影部分面积即可求解.
解:由图可知,大正方形减小正方形剩下的部分面积为;
拼成的长方形的面积:,
所以得出:,
故选:B.
【点拨】本题考查了平方差公式与图形面积,数形结合是解题的关键.
10.D
【分析】图1:四个全等的四边形的面积等于大正方形的面积减去小正方形的面积;图2:四个全等的四边形的面积等于平行四边形的面积,由此即可得.
解:图1:四个全等的四边形的面积为,
图2:四个全等的四边形的面积为,
则可以验证的乘法公式是,
故选:D.
【点拨】本题考查了平方差公式与几何图形,正确找出图形之间的面积关系是解题关键.
11.D
【分析】用代数式表示左图,右图阴影部分的面积即可.
解:左图阴影部分的面积可以看作两个正方形的面积差,即,而右图阴影部分是长为,宽为的长方形,因此面积为,
所以,
故选:D.
【点拨】本题考查平方差公式的几何背景,掌握平方差公式的结构特征是正确解答的前提.
12.B
【分析】根据图形确定出图1与图2中阴影部分的面积,即可作出判断.
解:根据题意得:图1中阴影部分的面积为,
图2中阴影部分的面积,
根据图1与图2中阴影部分的面积相等可得,
故选:B.
【点拨】此题考查了完全平方公式的几何背景,弄清阴影部分面积的求法是解本题的关键.
13.D
【分析】先用含有a、b的代数式分别表示,,再根据,整理可得结论.
解:由题意可得:;
;
∵,
∴,
∴,
∵,
∴,
∴.
故选:D.
【点拨】本题考查了整式的混合运算的应用,数形结合并熟练运用完全平方公式和平方差公式是解题的关键.
14.A
【分析】根据完全平方公式,整式恒等变形,得出a,b,x,y之间的关系即可得到答案.
解:由图形可知,,,因此①②正确;
,故③正确;
将①②平方相加可得故④正确;
将①②平方相减可得,故⑤错误;
故选A.
【点拨】本题考查完全平方公式的应用,解题的关键是掌握完全平方公式的恒等变形.
15.B
【分析】根据阴影部分的面积等于两个正方形的面积减去空白部分的面积,即可求解.
解:根据题意得:阴影部分的面积为
故选:B
【点拨】本题主要考查了整式加减及乘法的应用,熟练掌握整式混合运算法则是解题的关键.
16.
【分析】阴影部分的面积可看作是最大的长方形的面积空白部分长方形的面积,据此求解即可.
解:由题意得:
.
故答案为:.
【点拨】本题主要考查列代数式,解答的关键是理解清楚题意找到等量关系.
17.
【分析】根据图形的面积不变原则,分别表示图形的面积即可.
解:根据图1,得图形的面积为;
根据图2,得图形的面积为;
∵图形的面积相等,
∴.
故答案为:.
【点拨】本题考查了图形面积的不同表示法,正确表示图形的面积是解题的关键.
18.张
【分析】根据长方形的面积,结合多项式乘多项式的运算法则确定所需卡片型号和数量即可.
解:操场长宽分别为和,
操场的面积为,
需要张型地垫,张型地垫,张型地垫,
即需要用到地垫的张数为张.
故答案为:张.
【点拨】本题考查了多项式乘多项式,解题的关键是熟练掌握多项式乘多项式的运算法则,长方形的面积的求法.
19.
【分析】用代数式表示各个部分的面积,再利用面积之间的和差关系得出答案.
解:1号卡片的面积为,,2号卡片的面积为,3号卡片的面积,
由拼图可知,长方形的长为,宽为,因此面积为,
各个部分面积和为,
因此有,
故答案为:.
【点拨】本题考查多项式的乘法与几何图形的面积,熟练的利用和图形的面积证明代数恒等式是解本题的关键.
20.
【分析】用长乘以宽,列出算式,根据多项式乘以多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.
解:∵
∴若要拼一个长为,宽为的大长方形,则需要A类张,B类张,C类张.
故答案为:.
【点拨】本题考查了多项式乘法与图形的面积,正确的计算是解题的关键.
21.
【分析】根据最大的长方形面积等于四个小长方形面积进行求解即可.
解:由题意得,
故答案为:.
【点拨】本题主要考查了多项式乘以多项式与图形面积,正确理解题意是解题的关键.
22.
【分析】连接BG,设BF=a,EF=b,可用含a、b的代数式分别表示阴影部分的面积和的面积,由于阴影部分的面积等于的面积,可得,再用含a的代数式表示阴影部分的面积和正方形ABCD的面积,即可求解.
解:连接BG,设BF=a,EF=b,
则,,
∵阴影部分的面积等于的面积,
∴,即,
∴,
正方形ABCD的面积为:,
∴阴影部分与正方形ABCD的面积比为:,
即比值为:,
故答案为:.
【点拨】本题考查列代数式,正确表示出三角形和小正方形的面积是解题的关键.
23.
【分析】根据正方形面积公式求出第一个图形的面积,根据平行四边形面积公式求出第二个图形的面积,即可求出答案.
解:∵第一个图形的面积是,
第二个图形的面积是:,
∴根据两个图形的阴影部分的面积相等得:,
故答案为:.
【点拨】本题考查了平方差公式的应用,解题的关键是能用算式表示出阴影部分的面积.
24. 1
【分析】根据图和图中阴影部分的面积相等列式进行计算即可得出答案;
原式可化为,再根据中的结论进行计算即可得出答案.
解:根据题意可得,
图中阴影部分的面积为:,
图中长方形的长为,宽为,
面积为:,
则两个图形阴影部分面积相等,;
故答案为:;
(2)
.
故答案为:.
【点拨】本题主要考查了平方差公式的几何背景,熟练掌握平方差公式的几何背景问题的解决方法进行求解是解决本题的关键.
25.
【分析】分别求出左右两边图形中阴影部分的面积,即可求解.
解:左边图形中阴影部分的面积为,
右边图形中阴影部分的面积为,
∴验证了公式.
故答案为:
【点拨】本题主要考查了平方差公式与面积恒等式,利用数形结合思想解答是解题的关键.
26.30
【分析】用含a、b的代数式先表示出两个正方形的面积差,再利用a、b表示出阴影部分的面积,代入计算即可.
解:∵大正方形ABCM的边长为a,小正方形EBDN的边长为b,大正方形与小正方形的面积差为60,
∴,,
∴
,
故答案为:30.
【点拨】本题考查了平方差公式的应用,掌握正方形、三角形的面积公式是解决本题的关键.
27.a2﹣b2=(a+b)(a﹣b)
【分析】首先分别求出甲乙两图阴影部分的面积,然后根据面积相等可直接求得等式.
解:∵S甲=(a2﹣b2),S乙=(a+b)(a﹣b)
又∵S甲=S乙
∴a2﹣b2=(a+b)(a﹣b)
故答案为:a2﹣b2=(a+b)(a﹣b)
【点拨】本题考查了平方差公式与图形面积,根据题意表示出阴影部分面积是解题的关键.
28.10.4
【分析】在一块边长为a的正方形纸板四角,各剪去一个边长为b的正方形,那么剩余部分的面积=a2-4b2,利用平方差公式分解因式,然后代入数值计算即可求解.
解:由题意得:剩余部分的面积=a2-4b2=(a+2b)(a-2b),
当,时,剩余部分的面积=(3.6+2×0.8)×(3.6-2×0.8)=5.2×2=10.4.
故答案是:10.4.
【点拨】此题主要考查了因式分解的应用,解题的关键是利用正方形的面积公式和熟练进行因式分解.
29.①②③④
【分析】分别在两个图形中表示出阴影部分的面积,进而可得出验证公式.
解:在图①中,左边的图形阴影部分的面积,右边的图形阴影部分的面积,故可得:,可以验证平方差公式;
在图②中,左边的图形阴影部分的面积,右边的图形阴影部分的面积,故可得:,可以验证平方差公式;
在图③中,左边的图形阴影部分的面积,右边的图形阴影部分的面积,故可得:,可以验证平方差公式;
在图④中,左边的图形阴影部分的面积,右边的图形阴影部分的面积,故可得:,可以验证平方差公式.
【点拨】本题主要考查了平方差公式,运用不同的方法表示出阴影部分的面积是解本题的关键.
30.3
【分析】设大、小正方形边长为a、b,则a2=15,然后利用图中阴影部分的面积总和为6,进而可得正方形EFGH的面积.
解:设大、小正方形边长为a、b,
则有a2=15,阴影部分面积
,
即a2-b2=12,
可得b2=3,
即所求面积是3.
故答案为:3.
【点拨】本题考查了平方差公式与图形的面积,解决本题的关键是找准图形间的面积关系.
31.(1) (2)
【分析】(1)利用平移可得阴影部分面积为,再利用多项式乘多项式法则计算可得;
(2)空白部分面积为,再利用多项式乘多项式法则计算可得.
(1)解:阴影部分面积为
;
(2)解:空白部分的面积为
.
【点拨】本题考查了列代数式和整式的乘法运算,解决本题的关键是利用平移将阴影部分拼在一起.
32.(1) (2)
【分析】(1)阴影部分的面积两个三角形的面积之和,从而可得答案;
(2)利用非负数的性质先求解,,再代入(1)中的代数式进行计算即可.
(1)解:阴影部分的面积
;
(2)∵,
∴,,
解得:,,
,
∴阴影部分的面积为.
【点拨】本题考查的是整式的乘法运算与图形的面积关系,求解代数式的值,非负数的性质,正确的列出代数式是解本题的关键.
33.长方形的面积是
【分析】设圆长方形的长是,则宽是.根据把长截去剩余的面积刚好比把宽截去剩余的面积多,即可列方程求得x的值,进而求得宽,则面积即可求解.
解:设圆长方形的长是,则宽是.
根据题意得:,
∴,
解得:,
则宽是,
则长方形的面积是.
【点拨】本题考查了一元一次方程的应用,整式的乘法运算,正确列出方程是解题的关键.
34.(1) ;;(2) (3)
【分析】(1)根据图形的和差关系表示出,根据长方形的面积公式表示出;
(2)由(1)中的结果可验证的乘法公式是;
(3)由(2)中所得公式,可得原式,从而简便计算出该题结果.
(1)解:由题意得,,
.
故答案为:;;
(2)解:由(1)中的结果可验证的乘法公式为.
故答案为:;
(3)解:由(2)中所得乘法公式可得,
.
【点拨】本题考查了平方差公式几何背景的应用能力,掌握图形准确列式验证平方差公式,并能利用所验证公式解决相关问题是关键.
35.(1)(2) 5
【分析】(1)用含或的代数式表示拼成的新的长方形的长和宽即可求周长;
(2)当,时,代入(1)所得长方形的长和宽即可写出拼成的新的长方形的面积.
解:(1)
;
拼成的新的长方形纸板的周长为.
(2)当,时,
矩形的面积为:.
故答案为:5.
【点拨】本题考查了平方差公式的几何背景,解决本题的关键是确定拼成的长方形的长和宽.
36.(1) (2) (3)
【分析】(1)图①的面积为两个正方形的面积差,即;
(2)拼成的长方形的长为,宽为,可表示面积;
(3)由(1)(2)所表示的面积相等可得等式.
(1)解:根题意可得,
.
故答案为:;
(2)解:根据题意可得,
长方形的长为,宽为,
故答案为:;
(3)解:,
即.
故答案为:
【点拨】本题考查平方差公式,掌握平方差公式的结构特征是正确应用的前提.
37.(1) ,,(2) ①;②;
(3)
【分析】(1)分别用代数式表示图1、图2中阴影部分的面积即可;
(2)利用平方差公式进行计算即可;
(3)配上因式后,连续利用平方差公式进行计算,得出答案.
(1)解:图(1)中阴影部分的面积可以看作两个正方形的面积差,即,
图(2)中阴影部分是长为,宽为的长方形,
因此其面积为,
由于图1、图2阴影部分的面积相等可得,,
故答案为:,,;
(2)解:①
;
②
;
(3)解:
.
【点拨】本题考查平方差公式、完全平方公式的几何背景,用代数式表示图1、图2中阴影部分的面积是正确解答的前提.
38.(1) (2) 图②的面积为;图③的面积为;
(3) ;
【分析】(1)根据剩余的L型纸片的面积等于大正方形的面积减去小正方形的面积,即可求解;
(2)根据题意得:根据分割法图②是由2个上下底分别为a,b,高为的梯形;图③是由2个边长分别为,b的长方形和边长为的正方形组成,即可求解;
(3)结合(1),(2)写出等式,即可.
(1)解:根据题意得:图①中剩余的L型纸片的面积是;
故答案为:
(2)解:根据题意得:根据分割法图②是由2个上下底分别为a,b,高为的梯形;图③是由2个边长分别为,b的长方形和边长为的正方形组成,
所以图②的面积为;
图③的面积为;
(3)恒等式为;.
【点拨】本题主要考查了平方差公式的应用,利用数形结合思想解答是解题的关键.
39.(1) (2)
【分析】(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,一种是大正方形的面积,可得等式;
(2)利用(1)中的等式变形后,直接代入求得答案即可;
解:(1);
(2)∵,,
∴;
【点拨】本题考查了完全平方公式几何意义,解题的关键是注意图形的分割与拼合,会用不同的方法表示同一图形的面积.
(1) (2) (3)
(4) ,见分析
【分析】(1)图②中阴影部分为边长为的正方形,从而其面积可求;
(2)大正方形的面积减去长方形的面积可得阴影部分的面积,也可得出三个代数式,,之间的等量关系;
(3)由(2)所得出的关系式,可求出,从而可求出的值;
(4)可参照第四题画图.
(1)解:根据题意得图②中阴影部分为边长为的正方形,
∴阴影部分的面积为,
故答案为:;
(2)解:最外层大正方形的面积为,4个长方形的面积为,
阴影部分面积为,总体看图形的面积和部分之和的面积相等,
∴,
故答案为:;
(3)解:∵,
∴,
∴,
(4)解:,
画出一个几何图形,如下:
【点拨】本题考查了完全平方公式的几何背景,数形结合、明确图形的面积表达方式,是解题的关键.
41.(1);(2).
【分析】(1)由长方形的面积减去正方形的面积,再列式计算即可;
(2)把,代入(1)中的代数式计算即可.
(1)解:绿化面积
.
∴绿化的面积为
(2)当,时,
绿化的面积.
∴当,时,绿化的面积是.
【点拨】本题考查的是列代数式,求解代数式的值,整式的乘法与完全平方公式的实际应用,理解题意,列出正确的运算式是解本题的关键.
42.(1) (2) (3) (4)
【分析】(1)图①的面积是,图②的面积是,由此即可求解;
(2)根据(1)的结论,代入计算即可求解;
(3)将图形中各部分的面积通过图形面积计算公式表示出来并等于大长方形的面积即可求解;
(4),并计算出,分别求出,,根据图中阴影部分面积和,由此即可求解.
(1)解:中间部分的面积可以看作从边长为的正方形面积减去个长为,宽为的长方形面积,即,
∴,
故答案为:.
(2)解:∵,,,
∴
,
故答案为:.
(3)解:分别以大矩形的面积和几个小矩形的面积为等量可得:,
故答案为:.
(4)解:∵,,
∴①,
∴,
∴,
∴,
∵,且,
∴②,
①+②得,,
∴,
图中阴影部分面积和
.
【点拨】本题主要考查多项式与多项式的乘法,乘法公式与图形面积,掌握整式的乘法运算法则是解题的关键.
43.(1) (2) (3) ①;②
【分析】(1)由图2可知该长方形的长为,宽为,从而由长方形面积公式即可得出答案;
(2)由图1和图2的阴影部分面积相等,即得出;
(3)由平方差公式和完全平方公式计算即可.
解:(1)图2中的阴影部分面积为.
故答案为:;
(2)由(1)可以得到乘法公式:.
故答案为:;
(3)解:①
;
②
.
.
【点拨】本题考查平方差公式和完全平方公式.利用数形结合的思想是解答本题的关键.
44.(1) (2) (3)
【分析】(1)直接利用公式进行计算即可;
(2)把化为,再利用公式进行计算即可;
(3)由,可得,再利用公式计算即可.
(1)解:.
(2).
(3)∵,,
∴,
∵,,
∴
.
【点拨】本题考查的是完全平方公式的几何意义,完全平方公式的应用,灵活应用完全平方公式解决问题是解本题的关键.
45.(1) (2) 见分析(3) D
【分析】(1)看图即可得出所求的式子;
(2)画出的长方形边长分别为和即可;
(3)根据图中每个图形的面积之间的关系,结合完全平方公式的变形和平方差公式,即可判断出正确的有几个.
(1)解:根据题意得:大长方形的长,宽分别为;大长方形是由2边长为a的正方形,5个小长方形,2个边长为b的正方形组成的,
∴图③所表示的等式为:;
故答案为:
(2)解:∵长方形面积为,
∴该大长方形可以看作是由2边长为a的正方形,7个小长方形,3个边长为b的正方形组成的,
画出示意图如下:
(3)解:根据题意得:,
∴,故①正确;
观察图形得:,故②正确;
观察图形得:,,
∴,故③正确;
观察图形得:,,
∴,,
两式相加得:,
∴,故④正确;
故正确的有4个,
故答案为:D.
【点拨】本题考查了完全平方公式,整式的混合运算的应用,主要考查学生的计算能力和观察图形的能力.
46.(1)(2)(3)①16,②
【分析】(1)阴影部分为边长为的正方形,然后根据正方形的面积公式求解;
(2)在图中,大正方形有由小正方形和个矩形组成,则;
解:(1)阴影部分是边长为的正方形,
∴阴影部分的面积是;
故答案为:;
(2)由图可得
故答案为:.
(3)∵,
∴①,
②.
【点拨】本题考查了完全平方公式的几何背景:利用面积法证明完全平方公式.
47.(1) (2) 8(3) 36
【分析】(1)根据图象分别用两种方法表示出大长方形的面积即可求解;
(2)根据题意用正方形的面积加上正方形的面积减去和面积求解即可;
(3)由题意可得,,进而得到,然后表示出所有裁剪线(虚线部分)的长度之和,进而求解即可.
解:(1)大长方形的面积可以表示为,
大长方形的面积还可以表示为,
∴
故答案为:;
(2)
∵,,
∴原式;
(3)∵每块小长方形的面积为6,四个正方形的面积之和为48,
∴,
∴
∵
∴
∴裁剪线长为
∴图中所有裁剪线(虚线部分)长之和为36 cm
【点拨】此题考查整式的混合运算,掌握基本平面图形的面积计算方法是解决问题的关键.
48.(1) (2) ,画图见分析
【分析】(1)利用等面积法,使用两种方法求出面积,一种是直接计算大图形的面积,二是根据图形求出四个小图形面积,二者相同即可;
(2)根据题意可作出如图所示矩形,同(1)类似,求各个小图形面积和即可.
解:(1)图②面积可表示为:
面积还可表示为:
∴可得:,
故答案为:;
(2)如图所示:
根据图形求面积可得,大面积可表示为:,
两个小矩形面积和为:,
二者表示为同一图形面积,
∴.
【点拨】题目主要考查多项式与多项式相乘与几何图形结合进行验证多项式法则,理解并学会作出合适的图形是解题难点.
49.(1);(2).
【分析】(1)直接利用完全平方公式展开得、,然后通过计算两者之差,得到三者关系;
(2)求阴影部分面积,则需要求的值,正方形边长都相等,所以设,,能得到,两个正方形的面积和为32,即,再利用完全平方公式的变形进行应用计算.
(1)解:
;
故答案为:4ab;
(2)解:设,,则,,
.
.
【点拨】本题主要考查了完全平方公式的变形应用,熟练记忆完全平方公式是解题的关键.
50.(1) a-b(2) (3) 16
【分析】(1)由大、小正方形的边长与长方形边长之间的关系求解即可;
(2)根据题意可得图2中大正方形的面积等于中间阴影部分正方形的面积加上4个小长方形的面积,进而即可求出,,ab之间的数量关系;
(3)将x+y=5,xy,代入(2)中得到的等式中求解即可.
解:(1)由大、小正方形的边长与长方形边长之间的关系可得,
阴影部分的正方形边长为a-b,
故答案为:a-b;
(2)∵图2中大正方形的面积=,阴影部分的正方形的面积=,4个小长方形的面积=4ab,
∵大正方形的面积等于中间阴影部分正方形的面积加上4个小长方形的面积,
∴,
故答案为:;
(3)∵
∴将x+y=5,xy代入得:,
解得:.
【点拨】本题考查完全平方公式的几何背景,掌握完全平方公式的变形是解决问题的关键.
浙教版七年级数学下册基础知识专项讲练 专题3.28 整式的乘除(中考真题专练)(基础篇)(专项练习): 这是一份浙教版七年级数学下册基础知识专项讲练 专题3.28 整式的乘除(中考真题专练)(基础篇)(专项练习),共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
浙教版七年级数学下册基础知识专项讲练 专题3.40 整式的乘除(全章复习与巩固)(基础篇)(专项练习): 这是一份浙教版七年级数学下册基础知识专项讲练 专题3.40 整式的乘除(全章复习与巩固)(基础篇)(专项练习),共14页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
浙教版七年级数学下册基础知识专项讲练 专题3.30 整式的乘除(运算与化简100题)(基础篇)(专项练习): 这是一份浙教版七年级数学下册基础知识专项讲练 专题3.30 整式的乘除(运算与化简100题)(基础篇)(专项练习),共76页。试卷主要包含了计算,先化简,再求值,用简便方法计算等内容,欢迎下载使用。













