2023-2024学年江西省抚州一中八年级（上）月考数学试卷（12月份）（含解析）

这是一份2023-2024学年江西省抚州一中八年级（上）月考数学试卷（12月份）（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列三个数中，能组成一组勾股数的是( )
A. 2，3，4B. 6，7，8C. 6，8，10D. 9，16，25
2.|− 3|的相反数是( )
A. −3B. − 3C. 3D. 3
3.有一组数据如下：5，6，7，a，9，它们的平均数是7，那么这组数据的方差是( )
A. 2B. 2C. 10D. 10
4.我国古代数学名著《九章算术》中记载：“今有共买琎，人出半，盈四：人出少半，不足三.问人数、价格几何？”意思是：一起去买琎(琎：一种像玉的石头)，每个人出12两，则多4两；每个人出13两，则不足3两.问人数、琎的价格分别是多少？如果设人数x人，琎的价格为y两，那么可列方程组为( )
A. 12x+4=y13x+3=yB. 12x−4=y13x+3=yC. 12x−4=y13x−3=yD. 12x+4=y13x−3=y
5.若2m−4与3m−1是同一个数的平方根，则m的值是( )
A. −3B. −1C. 1D. −3或1
6.在同一直角坐标系中，一次函数y=kx+b和y=bx+k的图象可能正确的是( )
A. B.
C. D.
二、填空题：本题共6小题，每小题3分，共18分。
7. 16的算术平方根是______．
8.如图，填写一个能使AB/​/CD的条件：______．
9.在同一平面直角坐标系中，已知一次函数y1=kx−2(k为常数，k≠0)和y2=x+1.若两函数的图象在第一象限相交于点P，点P的横坐标是2，则方程组kx−2=yx+1=y的解是______．
10.某校九年级(1)班40名同学中，14岁的有1人，15岁的有21人，16岁的有16人，17岁的有2人，则这个班同学年龄的中位数是______岁．
11.若点P在第二象限，且点P到x轴的距离是3，到y轴的距离是5，则点P的坐标是______．
12.已知在平面直角坐标系中A(−2 3,0)、B(2,0)、C(0,2).点P在x轴上运动，当点P与点A、B、C三点中任意两点构成直角三角形时，点P的坐标为______．
三、解答题：本题共11小题，共84分。解答应写出文字说明，证明过程或演算步骤。
13.(本小题6分)
(1)计算：( 5−1)( 5+1)+|1− 2|−(π−2)0+ 8；
(2)解方程组：x−2y=−32x+y=9．
14.(本小题6分)
如图，四边形ABCD中，∠C=90°，BD平分∠ABC，AD=3，E为AB上一点，AE=4，ED=5，求CD的长．
15.(本小题6分)
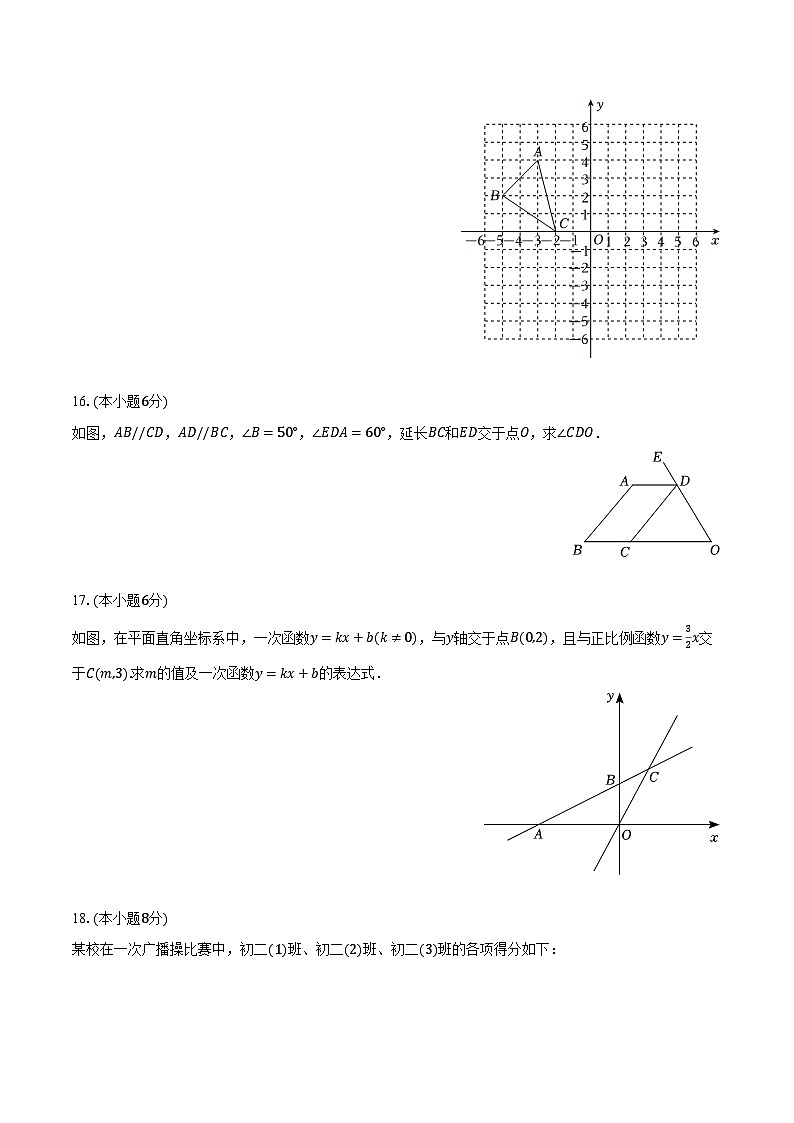
如图，在平面直角坐标系中，△ABC三个顶点均在格点上．
(1)在网格中作出△ABC关于y轴对称的图形△A1B1C1；
(2)直接写出B1的坐标；
(3)若网格的单位长度为1，求△A1B1C1的面积．
16.(本小题6分)
如图，AB/​/CD，AD//BC，∠B=50°，∠EDA=60°，延长BC和ED交于点O，求∠CDO．
17.(本小题6分)
如图，在平面直角坐标系中，一次函数y=kx+b(k≠0)，与y轴交于点B(0,2)，且与正比例函数y=32x交于C(m,3).求m的值及一次函数y=kx+b的表达式．
18.(本小题8分)
某校在一次广播操比赛中，初二(1)班、初二(2)班、初二(3)班的各项得分如下：
(1)填空：根据表中提供的信息，在服装统一方面，三个班得分的平均数是______；在动作整齐方面三个班得分的众数是______；在动作准确方面最有优势的是______班．
(2)如果服装统一、动作整齐、动作准确三个方面的重要性之比为2：3：5，那么这三个班的排名顺序怎样？为什么？
(3)在(2)的条件下，你对三个班级中排名最靠后的班级有何建议？
19.(本小题8分)
如图，在平面直角坐标系中，一次函数图象l1：y=−x+4与y轴、x轴分别交于点A，B，与正比例函数图象l2：y=13x交于点C．
(1)求点C的坐标；
(2)求△OBC的面积；
(3)若直线l3：y=kx+2与y轴交于点D，直线l3与直线l1交于点P，且△ADP的面积与△OBC的面积相等，求P点的坐标．
20.(本小题8分)
阅读材料：善于思考的小军在解方程组2x+5y=3①4x+11y=5②时.采用了一种“整体代换”的解法：
解：将方程②变形：4x+10y+y=5，即2(2x+5y)+y=5③．
把方程①代入③得：2×3+y=5，∴y=−1，
所以y=−1代入①得x=4，∴方程组的解为x=4y=−1．
请你解决以下问题：
(1)模仿小军的“整体代换”法解方程组3x−2y=5①9x−4y=19②；
(2)已知x，y满足方程组3x2−2xy+12y2=47①2x2+xy+8y2=36②，求x2+4y2的值．
21.(本小题9分)
如图，已知AB/​/CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F．
(1)当△PMN在如图1所示的位置时，求出∠PFD与∠AEM的数量关系．
(2)当△PMN在如图2所示的位置时，求证：∠PFD−∠AEM=90°，
(3)在(2)的条件下，若MN与CD交于点O，且∠DON=20°，∠PEB=30°，求∠N的度数．
22.(本小题9分)
元旦节当天，同学们为友谊长存，决定互送礼物，于是去某礼品店购进了一批礼品.已知购进3个A种礼品和2个B种礼品共需54元，购进2个A种礼品和3个B种礼品共需46元．
(1)A，B两种礼品每个的进价是多少元？
(2)该店计划用4200元全部购进A，B两种礼品，请你回答以下问题：
①设购进A种礼品x个，B种礼品y个，求y关于x的函数关系式．
②该店进货时，A种礼品不少于60个，已知A种礼品每个售价为20元，B种礼品每个售价为9元，若该店全部售完获利为W元，试说明如何进货获利最大？最大为多少元？
23.(本小题12分)
我们规定，有两组边相等，且它们所夹的角互补的两个三角形叫兄弟三角形.如图：OA=OB，OC=OD，∠AOB=∠COD=90°.回答下列问题：
(1)证明：△OAC和△OBD是兄弟三角形；
(2)取BD的中点P，连接OP，试证明AC=2OP.(小王同学根据要求的结论，想起老师上课讲的“中线倍长”的辅助线的构造方法)；
(3)求证：OP⊥AC．
答案和解析
1.【答案】C
【解析】解：A、22+32=4+9=13≠42，故2，3，4不是勾股数，不符合题意；
B、62+72=36+49=85≠82，故6，7，8不是勾股数，不符合题意；
C、62+82=36+64=100=102，故6，8，10是勾股数，符合题意；
D、92+162=81+256=337≠252，故9，16，25不是勾股数，不符合题意，
故选：C．
根据勾股数的定义逐项判断即可．
本题考查了勾股数的定义，勾股数就是可以构成一个直角三角形三边的一组正整数，熟练掌握勾股数的定义是解此题的关键．
2.【答案】B
【解析】解：|− 3|= 3的相反数是：− 3．
故选：B．
直接利用绝对值的性质结合相反数的定义得出答案．
此题主要考查了实数的性质，正确掌握相关定义是解题关键．
3.【答案】A
【解析】解：∵数据5，6，7，a，9的平均数是7，
∴5+6+7+a+95=7，
解得：a=8，
∴s2=15[(5−7)2+(6−7)2+(7−7)2+(8−7)2+(9−7)2]=2，
∴这组数据的方差是2．
故选：A．
根据算术平均数的计算公式求出a的值，根据方差的计算公式计算即可．
本题考查算术平均数和方差的计算，解题的关键是掌握方差的计算公式：一般地设n个数据，x1，x2，…，xn的平均数为x−，则方差为s2=1n[(x1−x−)2+(x2−x−)2+...+(xn−x−)2]．
4.【答案】B
【解析】解：根据题意得：12x−4=y13x+3=y，
故选：B．
根据“每个人出12两，则多4两；每个人出13两，则不足3两”列出方程组即可．
本题考查了由实际问题抽象出二元一次方程组的知识，解题的关键是找到等量关系．
5.【答案】D
【解析】解：当2m−4=3m−1时，m=−3，
当2m−4+3m−1=0时，m=1．
故选：D．
依据平方根的性质列方程求解即可．
本题主要考查的是平方根的性质，明确2m−4与3m−1相等或互为相反数是解题的关键．
6.【答案】B
【解析】解：A、一条直线反映k>0，b>0，一条直线反映k>0，b0，b0，b0，b0，b