备战中考数学《重难点解读•专项训练》专题13 最值模型：瓜豆原理-主从动点问题（知识解读）

这是一份备战中考数学《重难点解读•专项训练》专题13 最值模型：瓜豆原理-主从动点问题（知识解读），文件包含专题13最值模型瓜豆原理-主从动点问题知识解读-备战2023年中考数学《重难点解读•专项训练》全国通用原卷版docx、专题13最值模型瓜豆原理-主从动点问题知识解读-备战2023年中考数学《重难点解读•专项训练》全国通用解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
专题13 最值模型；瓜豆原理-主从动点问题（知识解读）
【专题说明】
初中数学有一类动态问题叫做主从联动，有的老师叫他瓜豆原理，也有的老师叫他旋转相似这类问题在解答的时候需要有轨迹思想，就是先要明确主动点的轨迹，然后要搞清楚主动点和从动点的关系，进而确定从动点的轨迹来解决问题．
【方法技巧】
瓜豆原理：一个主动点，一个从动点（根据某种约束条件，跟着主动点动），当主动点运动时，从动点的轨迹相同．（古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．）
满足条件：
1.两动一定；2.动点与定点的连线夹角是定角；3.动点到定点的距离比值是定值．
方法：第一步：找主动点的轨迹 ；第二步：找从动点与主动点的关系；
第三步：找主动点的起点和终点；第四步：通过相似确定从动点的轨迹，
第五步：根据轨迹确定点线、点圆最值．
“瓜豆原理”其实质就是构造旋转、相似．
涉及的知识和方法：
知识：①相似；②三角形的两边之和大于第三边；③点到直线之间的距离垂线段最短；④点到圆上点共线有最值．
模型一：运动轨迹为圆弧
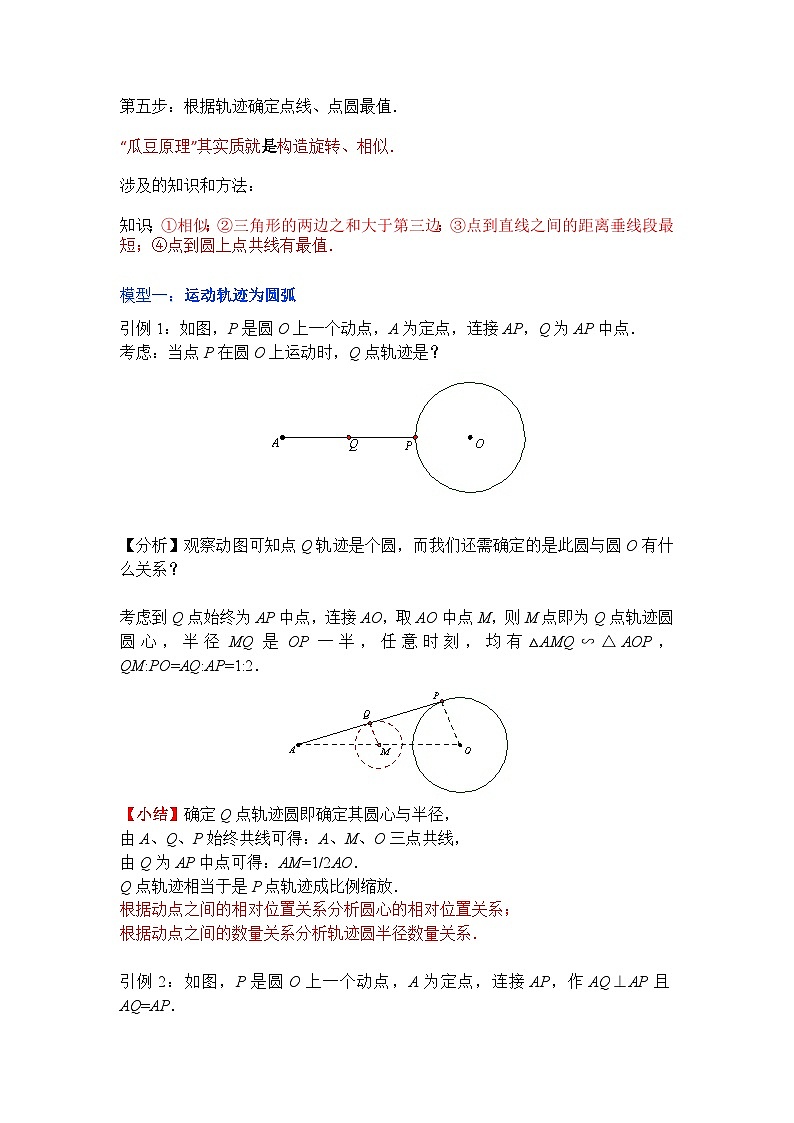
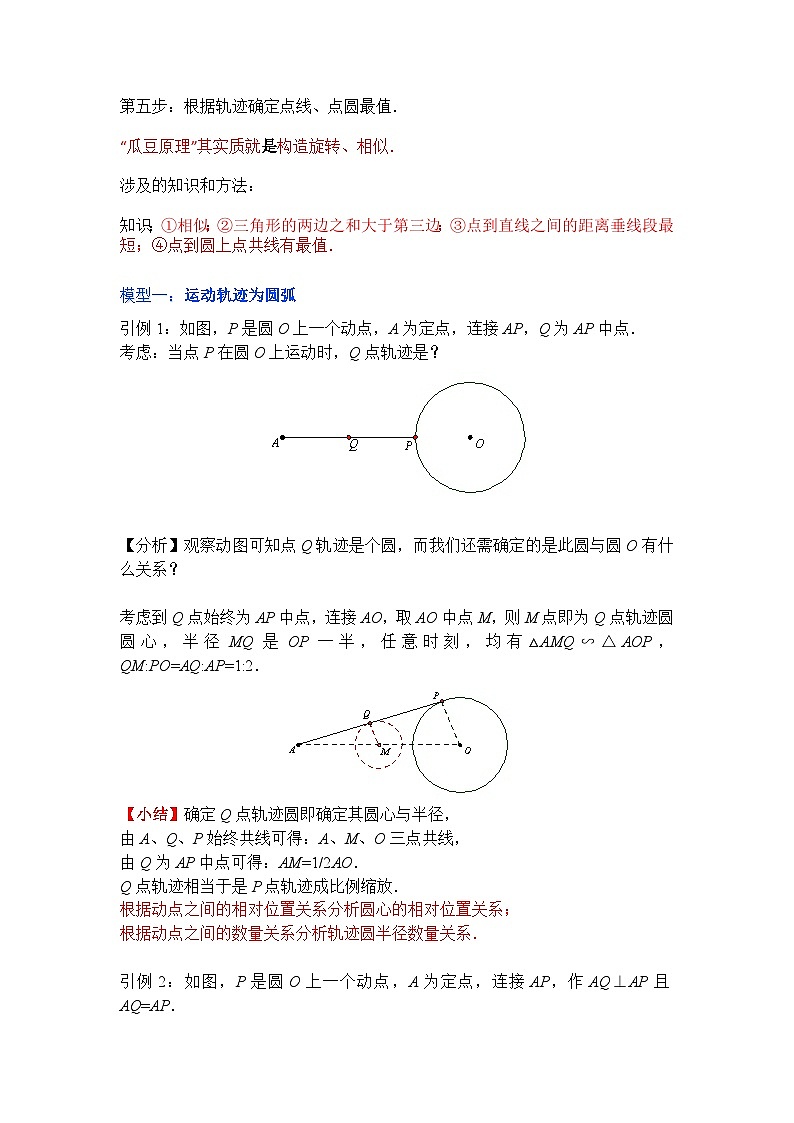
引例1：如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．
考虑：当点P在圆O上运动时，Q点轨迹是？
【分析】观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？
考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．
【小结】确定Q点轨迹圆即确定其圆心与半径，
由A、Q、P始终共线可得：A、M、O三点共线，
由Q为AP中点可得：AM=1/2AO．
Q点轨迹相当于是P点轨迹成比例缩放．
根据动点之间的相对位置关系分析圆心的相对位置关系；
根据动点之间的数量关系分析轨迹圆半径数量关系．
引例2：如图，P是圆O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．
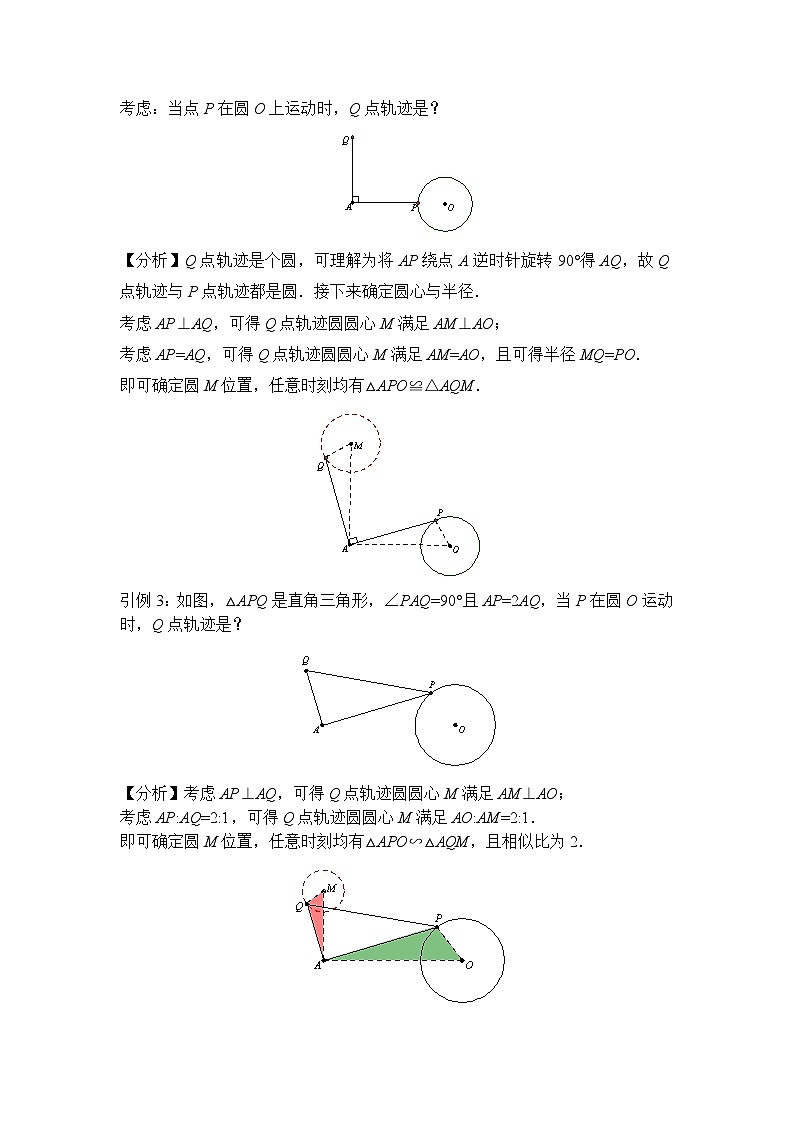
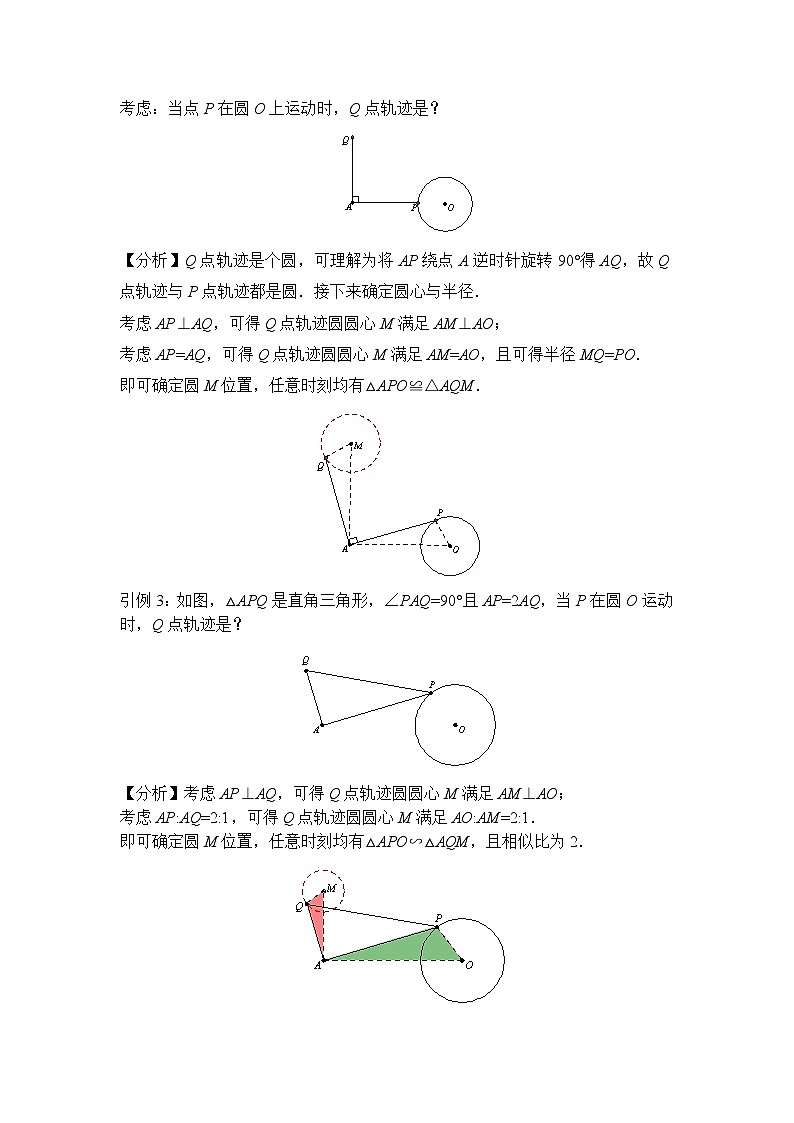
考虑：当点P在圆O上运动时，Q点轨迹是？

【分析】Q点轨迹是个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P点轨迹都是圆．接下来确定圆心与半径．
考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；
考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．
即可确定圆M位置，任意时刻均有△APO≌△AQM．
引例3：如图，△APQ是直角三角形，∠PAQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？
【分析】考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；
考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1．
即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．
【模型总结】
为了便于区分动点P、Q，可称点P为“主动点”，点Q为“从动点”．
此类问题的必要条件：两个定量
主动点、从动点与定点连线的夹角是定量（∠PAQ是定值）；
主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．
【结论】（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：
∠PAQ=∠OAM；
（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比：
AP:AQ=AO:AM，也等于两圆半径之比．
按以上两点即可确定从动点轨迹圆，Q与P的关系相当于旋转+伸缩．
模型二：运动轨迹为线段
引例：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？
【分析】当P点轨迹是直线时，Q点轨迹也是一条直线．
可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．
【引例】如图，△APQ是等腰直角三角形，∠PAQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？
【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．
当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q点的起始位置和终点位置，连接即得Q点轨迹线段．
【模型总结】
必要条件：
主动点、从动点与定点连线的夹角是定量（∠PAQ是定值）；
主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．
结论：
P、Q两点轨迹所在直线的夹角等于∠PAQ（当∠PAQ≤90°时，∠PAQ等于MN与BC夹角）
P、Q两点轨迹长度之比等于AP:AQ（由△ABC∽△AMN，可得AP:AQ=BC:MN）
【典例分析】
【典例1】如图，正方形ABCD的边长为5，E为BC上一点，且BE＝2，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为（ ）
A．2B．2.5C．3D．3.5
【答案】D
【解答】解：由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动，
将△EFB绕点E旋转60°，使EF与EG重合，得到△EFB≌△EHG，
∴BE＝EH，∠BEH＝60°，∠GHE＝90°，
∴△EBH为等边三角形，点G在垂直于HE的直线HN上，
作CM⊥HN，则CM即为CG的最小值，
作EP⊥CM，可知四边形HEPM为矩形，
∴∠PEC＝180°﹣∠PEH﹣∠BEH＝180°﹣90°﹣60°＝30°，
∴PC＝CE，
则CM＝MP+CP＝HE+EC＝2+＝，
故选：D．
【变式1-1】如图，在矩形ABCD中，AB＝5，BC＝5，点P在线段BC上运动（含B、C两点），连接AP，以点A为中心，将线段AP逆时针旋转60°到AQ，连接DQ，则线段DQ的最小值为（ ）
A．B．C．D．3
【答案】A
【解答】解：如图，以AB为边向右作等边△ABF，作射线FQ交AD于点E，过点D作DH⊥QE于H．
∵四边形ABCD是矩形，
∴∠ABP＝∠BAD＝90°，
∵△ABF，△APQ都是等边三角形，
∴∠BAF＝∠PAQ＝60°，BA＝FA，PA＝QA，
∴∠BAP＝∠FAQ，
在△BAP和△FAQ中，
，
∴△BAP≌△FAQ（SAS），
∴∠ABP＝∠AFQ＝90°，
∵∠FAE＝90°﹣60°＝30°，
∴∠AEF＝90°﹣30°＝60°，
∵AB＝AF＝5，AE＝AF÷cs30°＝，
∴点Q在射线FE上运动，
∵AD＝BC＝5，
∴DE＝AD﹣AE＝，
∵DH⊥EF，∠DEH＝∠AEF＝60°，
∴DH＝DE•sin60°＝×＝，
根据垂线段最短可知，当点Q与H重合时，DQ的值最小，最小值为，
故选：A．
【变式1-2】如图，长方形ABCD中，AB＝3，BC＝4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，将EF绕着点E顺时针旋转45°到EG的位置，连接FG和CG，则CG的最小值为（ ）
A．2B．1+C．2D．
【答案】B
【解答】解：如图，将线段BE绕点E顺时针旋转45°得到线段ET，连接GT，连接DE交CG于J．
∵四边形ABCD是矩形，
∴AB＝CD＝3，∠B＝∠BCD＝90°，
∵∠BET＝∠FEG＝45°，
∴∠BEF＝∠TEG，
在△EBF和△ETG中，
，
∴△EBF≌△ETG（SAS），
∴∠B＝∠ETG＝90°，
∴点G的在射线TG上运动，
∴当CG⊥TG时，CG的值最小，
∵BC＝4，BE＝1，CD＝3，
∴CE＝CD＝3，
∴∠CED＝∠BET＝45°，
∴∠TEJ＝90°＝∠ETG＝∠JGT＝90°，
∴四边形ETGJ是矩形，
∴DE∥GT，GJ＝TE＝BE＝1，
∴CJ⊥DE，
∴JE＝JD，
∴CJ＝DE＝，
∴CG＝CJ+GJ＝1+，
∴CG的最小值为1+，
故选：B．
【变式1-3】（2021·四川绵阳·中考真题）如图，在中，，，，且，若，点是线段上的动点，则的最小值是（ ）
A．B．C．D．
【答案】A
【解答】解：，，，解得：（负值舍去），
，，，，，
，，过B作于H，
，，
，，当时，PQ的值最小，
，，，，故选：A．
【变式1-4】（2021·四川广元·中考真题）如图，在中，，，点D是边的中点，点P是边上一个动点，连接，以为边在的下方作等边三角形，连接．则的最小值是（ ）
A．B．1C．D．
【答案】B
【解答】解：以CD为边作等边三角形CDE，连接EQ，如图所示：
∵是等边三角形，∴，
∵∠CDQ是公共角，∴∠PDC=∠QDE，∴△PCD≌△QED（SAS），
∵，，点D是边的中点，
∴∠PCD=∠QED=90°，，∴点Q是在QE所在直线上运动，
∴当CQ⊥QE时，CQ取的最小值，∴，∴；故选B．
【变式1-5】（2022·湖北·鄂州市三模）如图，在边长为的正方形中，是边的中点，是边上的一个动点不与重合，以线段为边在正方形内作等边，是边的中点，连接，则在点运动过程中，的最小值是（ ）
A．B．C．D．
【答案】C
【解答】解：∵P是边AD的中点，AD=6，∴AP=3，如图，连接AM，
∵等边，是边的中点，∴AM平分∠EAF，
∴在点运动过程中，点M在∠EAF的平分线上，∴当AM⊥PM时，PM取得最小值，
∵是等边的边的中点，∴PM⊥AM， ∠EAM=30°，
∴∠PAM=60°，∴PM=AP=，故选：C．
【变式1-6】（2022·山东日照·中考真题）如图，在平面直角坐标系xOy中，点A的坐标为（0，4），P是x轴上一动点，把线段PA绕点P顺时针旋转60°得到线段PF，连接OF，则线段OF长的最小值是__________．
【答案】2
【解答】解：∵将线段PA绕点P顺时针旋转60°得到线段PF，
∴∠APF=60°，PF=PA，∴△APF是等边三角形，∴AP=AF，
如图，当点F1在x轴上时，△P1AF1为等边三角形，则P1A=P1F1=AF1，∠AP1F1=60°，
∵AO⊥P1F1，∴P1O=F1O，∠AOP1=90°，∴∠P1AO=30°，且AO=4，
由勾股定理得：，∴，∴点F1的坐标为，
如图，当点F2在y轴上时，∵△P2AF2为等边三角形，AO⊥P2O，∴AO=F2O=4，∴点F2的坐标为（0，-4），
∵，∴∠OF1F2=60°，
∴点F运动所形成的图象是一条直线，∴当OF⊥F1F2时，线段OF最短，设直线F1F2的解析式为y=kx+b，
则，解得，∴直线F1F2的解析式为y=x-4，
∵AO=F2O=4，AO⊥P1F1，∴，在Rt△OF1F2中，OF⊥F1F2，
设点O到F1F2的距离为h，则，
∴，解得h=2，即线段OF的最小值为2，故答案为2．
【变式1-7】（2022·福建福州模拟预测）如图，在平面直角坐标系中，是直线上的一个动点，将绕点逆时针旋转，得到点，连接，则最小值为______．
【答案】
【解答】设，过点作轴，过点作交于点，过点作交于点，
∵，∴.
∵，∴.
∵，∴，∴，.
∵，∴，，∴，
令，，∴，
∴点在直线上运动，当时，的值最小.
在中，令，则，令，则，∴，，∴．
∵，∴，∴，
在中，令，则，∴，∴.
∵，即，解得，所以的最小值为.故答案为：．
【典例2】如图，⊙O的直径AB＝2，C为⊙O上动点，连结CB，将CB绕点C逆时针旋转90°得到CD，连结OD，则OD的最大值为 ．
【答案】+1
【解答】解：如图，以OB为边在AB的下方作等腰直角三角形OBE，连接CE，BD，
∵将CB绕点C逆时针旋转90°得到CD，
∴BC＝CD，∠DCB＝90°，
∴∠DBC＝45°，BD＝BC，
∵△OBE是等腰直角三角形，
∴OE＝BE，∠OBE＝45°，OB＝BE＝1，
∴BE＝OE＝，
∵∠DBC＝∠OBE，
∴∠OBD＝∠CBE，
又∵＝，
∴△DBO∽△CBE，
∴，
∴OD＝CE，
∴当CE有最大值时，OD有最大值，
当点C，点O，点E三点共线时，CE有最大值为1+，
∴OD的最大值为+1，
故答案为：+1
【变式2-1】如图，在Rt△ABC中，∠ACB＝90°，AC＝16，BC＝12，点P在以AB为直径的半圆上运动，由点B运动到点A，连接CP，点M是CP的中点，则点M经过的路径长为 ．
【答案】5π
【解答】解：∵∠ACB＝90°，AC＝16，BC＝12，
∴AB＝＝＝20，
连接AP，BP，
∵AB是直径，
∴∠APB＝90°，
即AP⊥BP，
取BC，AC的中点E和F，连接ME，MF，EF，
在△BPC中，
∵M，E为PC、BC的中点，
∴ME∥BP，ME＝，
在△APC中，
∵点M、F为PC、AC的中点，
∴MF∥AP，MF＝，
∴ME⊥MF，
即∠EMF＝90°，
∴点M在以EF为直径的半圆上，
∴EF＝AB＝10，
∴点M的运动路径长为＝5π，
故答案为：5π．
【变式2-2】如图，已知点A是第一象限内的一个定点，若点P是以O为圆心，2个单位长为半径的圆上的一个动点，连接AP，以AP为边向AP右侧作等边三角形APB．当点P在⊙O上运动一周时，点B运动的路径长是 ．
【答案】4π
【解答】解：如图，连接AO、OP，将AO绕点A逆时针旋转60°，得线段AO'，连接O'B、OO'，
∵AO＝AO'，∠OAO'＝60°，
∴△OAO'为正三角形，
∵△APB为正三角形，
∴∠PAB＝60°，PA＝BA，
∴∠PAB﹣∠OAB＝∠OAO'﹣∠OAB，
∴∠PAO＝∠BAO，
在△APO与△ABO′中，
，
∴△APO≌△ABO′，
∴OP＝O'B＝2，
∴⊙O'即为动点B运动的路径，
∴当点P在⊙O上运动一周时，点B运动的路径长是4π，