




最新中考数学总复习真题探究与变式训练(讲义) 专题37 二次函数的性质综合题(4大类型)
展开一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
模块三 重难点题型专项训练
专题37 二次函数的性质综合题(4大类型)
考查类型一 交点问题
例1 (2022·山东烟台·统考中考真题)二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣,且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
A.①③B.②④C.③④D.②③
例2 (2022·湖北荆州·统考中考真题)规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
例3 (2022·山西·中考真题)阅读与思考
下面是小宇同学的数学小论文,请仔细阅读并完成相应的任务
任务:
(1)上面小论文中的分析过程,主要运用的数学思想是 (从下面选项中选出两个即可);
A.数形结合
B.统计思想
C.分类讨论.
D.转化思想
(2)请参照小论文中当时①②的分析过程,写出③中当时,一元二次方程根的情况的分析过程,并画出相应的示意图;
(3)实际上,除一元二次方程外,初中数学还有一些知识也可以用函数观点来认识,例如:可用函数观点来认识一元一次方程的解.请你再举出一例为
二次函数与X轴的交点有三种可能,分别是有两个交点、一个交点和无交点。在初中范围内,二次函数与Y轴始终有交点(当x=0时,y必有一个值)。在实际解题中,与Y轴的交点纵坐标的值,就是函数表达式中c的值。
二次函数与X轴若有两个交点,则求根公式大于0,如果一个交点,则求根公式等于0,如果无交点,则求根公式小于0。通常情况下,二次函数的求解中都是有两个交点。只是要注意,不同的题型,不同的情况下求解方法也不同。总之在求解中要灵活应用各种公式,巧妙应对,解题就变得轻巧。
二次函数与X轴交点的求解方法
以上简要介绍二次函数与X轴的交点,而在实际情况中,更加的复杂,下面从常见的四种情况进行解析:
1、无交点;如果二次函数与X轴无交点,则判别公式b^2-4ac<0,此时函数的图像要么位于X轴的上方,或者X轴的下方。如果与X轴无交点,相应的函数解析式在实数范围内也是无解,例如y=x^2-3x+5,y=3x^2+2x+6都是与X轴无交点。
如何判断无交点,有一个很好的经验可以直接判断,就是二次项和常数项系数为同号的时候,很可能无交点,如果二次项和常数项是异同,即一正一副的时候,肯定有交点,因为b^2是非负数,-4ac也是非负数。因此求根公式肯定是非负数。如果二次函数的解析式转化成y=a(x+h)^2+k的时候,如果a>0,k>0则一定与X轴无交点。
2、有一个交点;这种情况下求根公式等于0,函数解析式应该可以进行因式分解,并且是一个完全平方数,作为学生要对x+1,x-1,x+2,x-2等式子的完全平方式非常熟悉,一看就知道是完全平方式。常见的y=x^2+2x+1,或者y=x^2-2x+1都是完全平方式。
3、有两个交点;这种情况下求根公式大于0,通常情况下,二次函数都是与X轴有两个交点。这两个交点也有三种可能,第一种是一个交点在正半轴,一个交点在负半轴;第二种可能是两个都在正半轴;第三种可能是都在负半轴。
4、有交点;这个时候,一定要注意,有交点有两层含义,一层含义是有一个交点,第二层含义是有两个交点。部分同学只注意到有两个交点,疏忽有一个交点也算是有交点,犯错的原因是对题目意思没有理解。
二次函数与Y轴交点的求解方法
函数与Y轴的交点,要么在Y轴的正半轴,要么在Y轴的负半轴,还有一种特别情况,就是过原点,此时的函数解析式的常数项必是0。如果与Y轴的正半轴有交点,则常数项c大于0,如果与Y轴的负半轴有交点,则常数项c小于0。
通常在解题中,会出现这样的题型:
已知某二次函数经过(0,c),题目中会具体地指出c的值,这个时候,可以把函数解析式y=ax^2+bx+c得c的具体值直接带入解析式中,求解更加方便。
还有根据函数经过Y轴正半轴或者负半轴,可以肯定必定过哪个象限,如果经过Y轴的正半轴,则必定经过第二象限。如果经过Y轴负半轴,则必定经过第三象限。
【变式1】(2022·福建福州·福建省福州教育学院附属中学校考模拟预测)已知抛物线与轴的交点为和,点,是抛物线上不同于,的两个点,记的面积为,的面积为,有下列结论:
①当时,;
②当时,;
③当时,;
④当时,.
其中正确结论的序号是( )
A.②③B.①③C.①②③④D.③
【变式2】(2022·福建漳州·统考模拟预测)在平面直角坐标系中,已知函数,,,其中a,b,c是正实数,且满足.设函数,,的图象与x轴的交点个数分别为,,,则下列说法一定正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,则
【变式3】(2022·山东青岛·山东省青岛实验初级中学校考模拟预测)函数(a为常数)的图象与坐标轴只有两个交点,则______.
【变式4】(2022·浙江宁波·校考模拟预测)已知关于的方程的两个根分别是,若点是二次函数的图象与轴的交点,过作轴交抛物线于另一交点,则的长为 _____.
【变式5】(2021·江苏南通·统考一模)已知抛物线y=x2+2mx+m2﹣1(m是常数).
(1)求该抛物线与x轴交点坐标及顶点坐标(可用含m的代数式表示);
(2)将该抛物线先向右平移2个单位长度,再向上平移(2m﹣1)个单位长度,若平移后的抛物线与x轴没有公共点,且当x≤0时,y随x的增大而减小,求m的取值范围;
(3)已知A(1,1),B(3,1),若该抛物线与线段AB只有一个公共点,直接写出m的取值范围.
考查类型二 恒成立问题
例1 (2020·浙江嘉兴·统考中考真题)小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1
例2 (2021·浙江·统考中考真题)已知在平面直角坐标系中,点的坐标为是抛物线对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使为直角三角形的点的个数也随之确定.若抛物线的对称轴上存在3个不同的点,使为直角三角形,则的值是____.
例3 (2022·四川攀枝花·统考中考真题)如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为,点是其对称轴上一点,y轴上一点.
(1)求二次函数的表达式;
(2)二次函数在第四象限的图象上有一点P,连结,,设点P的横坐标为t,的面积为S,求S与t的函数关系式;
(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.
1、y>0恒成立:其实就是开口要向上,而且与x轴无交点,也就是建立y=0的方程,让△<0;
2、y≥0恒成立:比前一个多了个△=0的情况,所以就是△≤0,当然,开口要向上;
3、y<0恒成立:那么开口就要向下,同样与x轴无交点,判别式△<0;
4、y≤0恒成立:开口向下,其他同第2种;
5、y≥m或y≤m恒成立:其实就是y-m≥0或y-m≤0的形式,和前面没啥区别;
6、二次函数恒经过某坐标点:这种情况可能会相对较难,所以同学们在思考的时候一定要记得,肯定是某点的坐标代入后会将未知系数抵消,一定要记住这个切入点,然后根据情况进行变换;
7、然后就是和一次函数恒有交点:都是同样的方法;
【变式1】(2020·贵州遵义·统考二模)如图,二次函数图象经过,且有最小值,若A点关于y轴的对称点为B点,过B作y轴平行线交抛物线于点C,在的斜边上有一动点D,过D作于E,于F,则EF的最小值为( )
A.B.C.D.
【变式2】(2021·河北·统考一模)如图,抛物线y=a(x﹣1)2+k(a>0)经过点(﹣1,0),顶点为M,过点P(0,a+4)作x轴的平行线1,l与抛物线及其对称轴分别交于点A,B,H.以下结论:①当x=3.1时,y>0;②存在点P,使AP=PH;③(BP﹣AP)是定值;④设点M关于x轴的对称点为M',当a=2时,点M′在l下方,其中正确的是( )
A.①③B.②③C.②④D.①④
【变式3】(2022·浙江宁波·校考模拟预测)在平面直角坐标系中,若某函数图象上至少存在不同的两点关于y轴对称,则把该函数称之为“Y函数”,其图象上关于y轴对称的不同两点叫做一对“Y点”.若关于x的“Y函数”(,且a,b,c是常数)经过坐标原点O,且与直线l:(,且m,n是常数)交于两点,当满足时,则直线l经过的定点为 _____.
【变式4】(2022·浙江湖州·模拟预测)已知在平面直角坐标系xOy中,点A的坐标为(5,12),M是抛物线y=ax2+bx+1(a≠0)对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定,若抛物线y=ax2+bx+1(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是__.
【变式5】(2023·广西玉林·一模)已知二次函数的图象经过点.
(1)求该二次函数的表达式;
(2)二次函数图象与轴的另一个交点为,与轴的交点为,点从点出发在线段上以每秒个单位长度的速度向点运动,同时点从点出发,在线段上以每秒个单位长度的速度向点运动,直到其中一点到达终点时,两点停止运动,求面积的最大值;
(3)在点、运动的过程中,是否存在使与相似的时刻,如果存在,求出运动时间,如果不存在,请说明理由.
考查类型三 函数值最值问题
例1 (2022·四川自贡·统考中考真题)已知A(−3,−2) ,B(1,−2),抛物线y=ax2+bx+c(a>0)顶点在线段AB上运动,形状保持不变,与x轴交于C,D两点(C在D的右侧),下列结论:
①c≥−2 ;
②当x>0时,一定有y随x的增大而增大;
③若点D横坐标的最小值为−5,点C横坐标的最大值为3;
④当四边形ABCD为平行四边形时,a=.
其中正确的是( )
A.①③B.②③C.①④D.①③④
例2 (2021·内蒙古·统考中考真题)已知抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点在抛物线上,E是该抛物线对称轴上一动点.当的值最小时,的面积为__________.
例3 (2022·山东日照·统考中考真题)在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)当抛物线过点A时,求抛物线的解析式;
(2)证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;
(3)在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
方法总结
二次函数在自变量的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值。
解决二次函数最值问题,若遇见对称轴和取值范围都给定,可分为对称轴在取值范围内和不在取值范围内两种情形。
若对称轴在取值范围内,顶点为最值点,(开口向上为最小值,开口向下为最大值),离对称轴较远的一个端点为另一个最值点(前者是最大值则后者是最小值,否则为最大值)。
【变式1】(2021·宁夏吴忠·校考一模)如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,顶点的坐标为,是抛物线上一点,且在轴上方,则面积的最大值为( )
A.B.C.D.
【变式2】(2022·山东济南·统考一模)在平面直角坐标系中,若点P的横坐标和纵坐标相等,则称点P为雅系点.已知二次函数的图象上有且只有一个雅系点,且当时,函数的最小值为-6,最大值为-2,则的取值范围是( )
A.B.C.D.
【变式3】(2022·安徽合肥·合肥市五十中学西校校考三模)已知,点和点在二次函数的图象上,若点是该二次函数图象上任意一点,且满足.
(1)用含a的代数式表示b为_____;
(2)mn的最大值为_____.
【变式4】(2022·河北石家庄·二模)在中,,,的顶点P在BC上滑动,PM始终过点A,且,在点P滑动的过程中:
(1)当______时,;
(2)BD的最大值为______.
【变式5】(2022·吉林长春·校考模拟预测)在平面直角坐标系中,抛物线(a为常数).
(1)当在抛物线上,求m的值.
(2)当抛物线的最低点到直线的距离恰好是时,求a的值.
(3)已知、,连接.当抛物线与线段有交点时,记交点为P(点P不与A、B重合),将线段绕点P顺时针旋转得到线段,以、为邻边构造矩形.
①若抛物线在矩形内部的图象的函数值y随自变量x的增大而减小时,求a的取值范围.
②当抛物线在矩形内部(包含边界)图象所对应的函数的最大值与最小值的差为时,直接写出a的值.
考查类型四 其他性质综合问题
例1 (2022·四川宜宾·统考中考真题)已知抛物线的图象与x轴交于点、,若以AB为直径的圆与在x轴下方的抛物线有交点,则a的取值范围是( )
A.B.C.D.
例2 (2021·黑龙江齐齐哈尔·统考中考真题)如图,抛物线的解析式为,点的坐标为,连接:过A1作,分别交y轴、抛物线于点、:过作,分别交y轴、抛物线于点、;过作,分别交y轴、抛物线于点、…:按照如此规律进行下去,则点(n为正整数)的坐标是_________.
例3 (2022·广东深圳·统考中考真题)二次函数先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.
(1)的值为 ;
(2)在坐标系中画出平移后的图象并求出与的交点坐标;
(3)点在新的函数图象上,且两点均在对称轴的同一侧,若则 (填“”或“”或“”)
一般式:(,,为常数,);
知识点:二次函数图象的平移
由二次函数的性质可知,抛物线()的图象是由抛物线()的图象平移得到的.在平移时,不变(图象的形状、大小不变),只是顶点坐标中的或发生变化(图象的位置发生变化)。平移规律是“左加右减,上加下减”,左、右沿轴平移,上、下沿轴平移,即
.
因此,我们在解决抛物线平移的有关问题时,首先需要化抛物线的解析式为顶点式,找出顶点坐标,再根据上面的平移规律,解决与平移有关的问题,
注意:(1)a 的绝对值越大,抛物线的开口越小.
(2)理解并掌握平移的过程,由,的图象与性质及上下平移与左右平移的规律:将抛物线解析式转化成顶点式,确定其顶点坐标;保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
平移规律:概括成八个字“左加右减,上加下减”.
【变式1】(2022·浙江宁波·一模)已知A,B两点的坐标分别为,,线段上有一动点,过点M作x轴的平行线交抛物线于两点(P在Q的左侧).若恒成立,则a的取值范围为( )
A.B.C.D.
【变式2】(2022·辽宁鞍山·统考二模)如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A.B.C.D.
【变式3】(2022·广东·模拟预测)若抛物线的顶点为,抛物线的顶点为B,且满足顶点A在抛物线上,顶点B在抛物线上,则称抛物线与抛物线互为“关联抛物线”,已知顶点为M的抛物线与顶点为N的抛物线互为“关联抛物线”,直线MN与轴正半轴交于点D,如果,那么顶点为N的抛物线的表达式为_________
【变式4】(2021·安徽阜阳·统考一模)如图1,E是等边的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边,连接已知的面积(S)与BE的长(x)之间的函数关系如图2所示(为抛物线的顶点).
(1)当的面积最大时,的大小为______ .
(2)等边的边长为______ .
【变式5】(2022·山东德州·校考二模)在平面直角坐标系中,已知抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)当时,直接写出点A,C,D的坐标:A______,C______,D______;
(2)如图1,直线DC交x轴于点E,若,求a的值和CE的长;
(3)如图2,在(2)的条件下,若点N为OC的中点,动点P在第三象限的抛物线上,过点P作x轴的垂线,垂足为Q,交AN于点F;过点F作,垂足为H.设点P的横坐标为t,记.
①用含t的代数式表示f;
②设,求f的最大值.
【培优练习】
1.(2021·浙江·九年级自主招生)已知抛物线的顶点为坐标原点,过作两条互相垂直的直线分别与抛物线交于点、,连接.求边上的高的最大值为( )
A.B.C.D.
2.(2023秋·河北廊坊·九年级统考期末)如图,抛物线的对称轴为直线,若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是( )
A.B.C.D.
3.(2023秋·河北保定·九年级校考期末)定义:若函数,则该函数的最大值为( )
A.0B.2C.3D.4
4.(2023秋·福建泉州·九年级泉州五中校联考期末)已知、是一元二次方程的两个不相等的实数根,、是一元二次方程的两个不相等的实数根,其中.若,则的值为( )
A.8B.9C.12D.18
5.(2023秋·河北邢台·九年级邢台三中校考期末)已知二次函数的图象如图所示,点是坐标系的原点,点是图象对称轴上的点,图象与轴交于点,则下面结论:
;
关于的方程的解是,;
当时,;
当时,;
周长的最小值是.
正确的有( )
A.2个B.3个C.4个D.5个
6.(2022秋·河南商丘·九年级校考阶段练习)如图,在四边形ABCD中,,,,,,动点P从点D出发以每秒2个单位长度的速度沿着边运动,到达点C时停止运动;另一动点Q同时从点D出发,以每秒1个单位长度的速度沿着边向点C运动,到达点C时停止运动.设点P的运动时间为t,的面积为S,则S关于t的函数图象是( )
A.B.C.D.
7.(2023秋·山东济南·九年级校考期末)规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧),,线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )
A.B.
C.或D.或
8.(2021春·河南郑州·八年级校考期中)如图,中,,,,是线段上一个动点,以为边在外作等边.若是的中点,则的最小值为( ).
A.16B.18C.15D.21
9.(2022秋·浙江温州·九年级校考阶段练习)如图,在平面直角坐标系中,的边OA在x轴上,,,抛物线与OB交于C点,过点C作交AB于D点.若CD过的重心G,则点G的坐标为___________.
10.(2022秋·辽宁盘锦·九年级校考阶段练习)如图抛物线与轴交于,两点,与轴交于点,点是抛物线对称轴上任意一点,若点,,分别是,,的中点,连接,,则的最小值为______.
11.(2023秋·河北石家庄·九年级校考期末)在平面直角坐标系中,点,,连接,抛物线经过点,且与线段恰有一个公共点.
(1)抛物线的对称轴为直线___________;
(2)的取值范围为___________.
12.(2022秋·浙江温州·九年级校考期中)如图,已知A,B是抛物线上的点,线段,且轴,过A,B两点作半径为5的圆(圆心在下方),点P是圆上任意一点,连接,取的中点Q,将该抛物线下方的部分沿直线向上翻折,交y轴于点C,连接,则的最大值是______.
13.(2022秋·浙江宁波·九年级校联考期中)已知顶点为A的抛物线与顶点为C的抛物线交于,,则四边形的周长为______.
14.(2022秋·河北石家庄·九年级校考期末)小明以等腰三角形底边的中垂线和所在的直线建立平面直角坐标系.如图,,抛物线经过A、两点,点的坐标为___________;若一条与轴重合的直线以每秒3个单位长度的速度向右平移,分别交线段、和抛物线于点、和点,连接、.设直线移动的时间为秒,当的面积最大时,点的坐标为___________;若使是直角三角形,则___________.
15.(2022秋·重庆沙坪坝·九年级校考期中)某公司去年推出一种节能产品,售价元个与月销量个的函数关系如下表,成本为元个,同时每月还需支出固定广告费元
(1)请观察题中的表格,用所学过的一次函数或反比例函数的有关知识,写出与之间的函数关系式;
(2)若出售这种节能产品的月利润为元,请用含的代数式表示月利润,并求出当月销售量为个时的月利润;
(3)该公司去年每个月都销售了个这种节能产品.从今年一月份开始,因物价上涨,广告费每月上涨了元,产品成本增加了%,因此售价上调元,由此月销量减少.结果今年一月份的月利润比去年每个月的月利润减少了元.求的整数值.(参考数据:,,)
16.(2023秋·广东江门·九年级统考期末)已知关于x的一元二次方程.
(1)求证:无论a为任何实数,此方程总有两个不相等的实数根;
(2)如图,若抛物线与x轴交于点和点B,与y轴交于点C,连结与对称轴交于点D.
①求抛物线解析式和点B的坐标;
②若点P是抛物线上位于直线的上方一动点,连接、,过点P作轴,交于点M,求面积的最大值及此时点P的坐标.
17.(2023秋·广东惠州·九年级校考期末)已知O为坐标原点,抛物线与x轴相交于点,,与y轴交于点C,且O,C两点之间的距离为3,,点A,C在直线上.
(1)求点C的坐标.
(2)当随着x的增大而增大时,求自变量x的取值范围.
(3)将抛物线向左平移个单位,记平移后y随着x的增大而增大的部分为P,直线向下平移n个单位,当平移后的直线与P没有公共点时,求的最小值.
18.(2022秋·黑龙江哈尔滨·九年级校考期中)已知:如图,抛物线()交轴于、两点,交轴于点,直线:交轴于点,交轴于点.
(1)求抛物线的解析式;
(2)若为抛物线上一点,连接、,设点的横坐标为(),的面积为,求与函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,点在线段上,点是第二象限抛物线上一点,,,且,求点的坐标.
19.(2023秋·湖南邵阳·九年级统考期末)如图,抛物线与x轴交于点、B两点,顶点,过点A的直线与抛物线相交于点C,与抛物线对称轴DF交于点E,.
(1)求该抛物线解析式;
(2)在对称轴上是否存在一点M,使以点A、E、M为顶点的三角形与相似,若存在,求出点M的坐标;若不存在,请说明理由.
(3)点P是线段上一动点,过点P作直线轴交抛物线于点Q,当线段的长度最大时,求P点坐标与的最大值.
20.(2023秋·江西宜春·九年级统考期末)如图,抛物线与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作轴,垂足为点.
(1)求直线AB的函数解析式.
(2)动点P在线段OC上,从原点O出发以每秒1个单位的速度向点C移动,过点P作轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长为s个单位,求s与t的函数解析式,并写出t的取值范围.
(3)在(2)的条件下(不考虑点P与点O、C重合的情况),连接CM、BN,是否存在某一时刻使得四边形BCMN为菱形?若存在,请求出t的值,若不存在,请说明理由.
考查类型
考查类型一 交点问题
考查类型二 恒成立问题
考查类型三 函数值最值问题
考查类型四 其他性质综合题
新题速递
用函数观点认识一元二次方程根的情况
我们知道,一元二次方程的根就是相应的二次函数的图象(称为抛物线)与x轴交点的横坐标.抛物线与x轴的交点有三种情况:有两个交点、有一个交点、无交点.与此相对应,一元二次方程的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、无实数根.因此可用抛物线与x轴的交点个数确定一元二次方程根的情况
下面根据抛物线的顶点坐标(,)和一元二次方程根的判别式,分别分和两种情况进行分析:
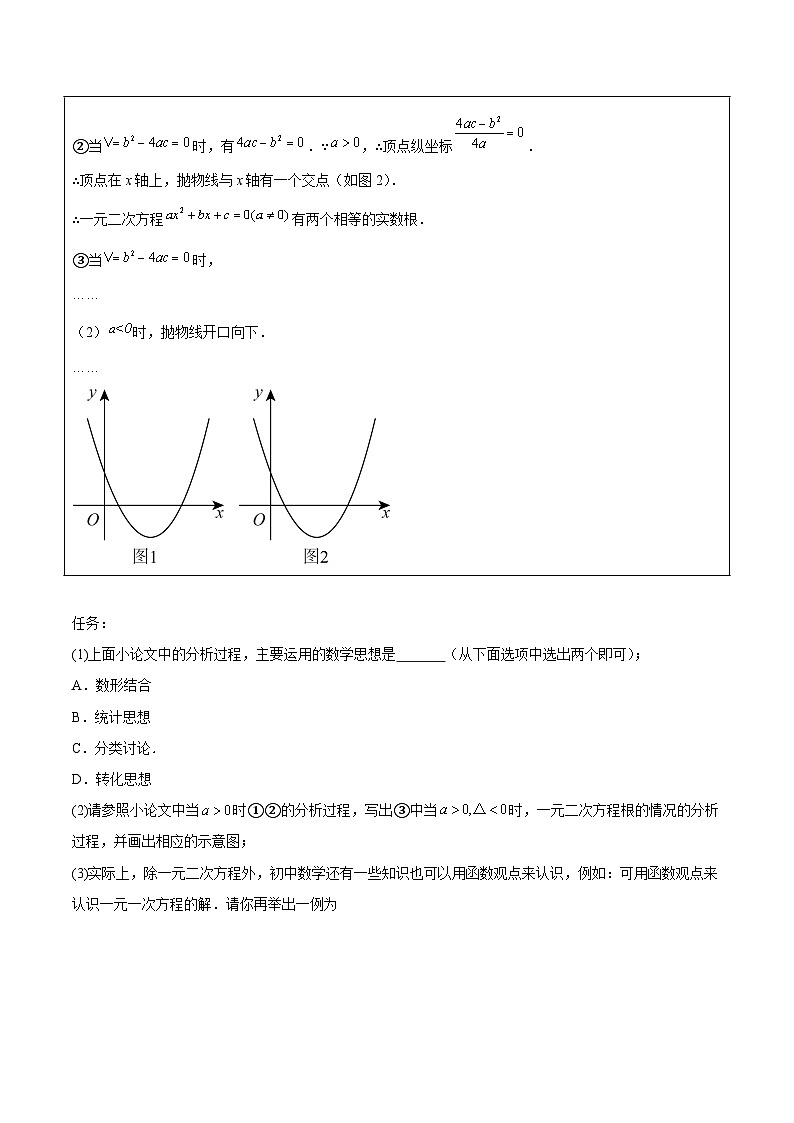
(1)时,抛物线开口向上.
①当时,有.∵,∴顶点纵坐标.
∴顶点在x轴的下方,抛物线与x轴有两个交点(如图1).
②当时,有.∵,∴顶点纵坐标.
∴顶点在x轴上,抛物线与x轴有一个交点(如图2).
∴一元二次方程有两个相等的实数根.
③当时,
……
(2)时,抛物线开口向下.
……
函数
二次函数(a、b、c为常数,a≠0)
图象
开口方向
向上
向下
对称轴
直线
直线
顶点坐标
增减性
在对称轴的左侧,即当时,y随x的增大而减小;在对称轴的右侧,即当时,y随x的增大而增大.简记:左减右增
在对称轴的左侧,即当时,y随x的增大而增大;在对称轴的右侧,即当时,y随x的增大而减小.简记:左增右减
最大(小)值
抛物线有最低点,当时,y有最小值,
抛物线有最高点,当时,y有最大值,
售价y(元/个)
…
月销量x(个)
…
最新中考数学总复习真题探究与变式训练(讲义) 专题35 实际应用题(5大类型): 这是一份最新中考数学总复习真题探究与变式训练(讲义) 专题35 实际应用题(5大类型),文件包含专题35实际应用题5大类型原卷版docx、专题35实际应用题5大类型解析版docx等2份试卷配套教学资源,其中试卷共108页, 欢迎下载使用。
最新中考数学总复习真题探究与变式训练(讲义) 专题34 规律探究性问题: 这是一份最新中考数学总复习真题探究与变式训练(讲义) 专题34 规律探究性问题,文件包含专题34规律探究性问题原卷版docx、专题34规律探究性问题解析版docx等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。
最新中考数学总复习真题探究与变式训练(讲义) 专题33 主从联动(瓜豆模型): 这是一份最新中考数学总复习真题探究与变式训练(讲义) 专题33 主从联动(瓜豆模型),文件包含专题33主从联动瓜豆模型原卷版docx、专题33主从联动瓜豆模型解析版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。












