




- 人教A版高二数学上学期重难点突破期末复习专题1.4 用空间向量研究距离、夹角问题(七个重难点突破)(2份打包,原卷版+解析版) 试卷 1 次下载
- 人教A版高二数学上学期重难点突破期末复习专题1.5空间向量的探索性问题(强化训练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 人教A版高二数学上学期重难点突破期末复习专题1.7空间向量与立体几何(六个混淆易错点)(2份打包,原卷版+解析版) 试卷 0 次下载
- 人教A版高二数学上学期重难点突破期末复习专题3.4双曲线的简单几何性质(九个重难点突破)(2份打包,原卷版+解析版) 试卷 0 次下载
- 人教A版高二数学上学期重难点突破期末复习专题3.5抛物线的标准方程及简单几何性质(八个重难点突破)(2份打包,原卷版+解析版) 试卷 0 次下载
人教A版高二数学上学期重难点突破期末复习专题1.6立体几何的最值、范围问题(强化训练)(2份打包,原卷版+解析版)
展开题型一数量积的最值范围范围
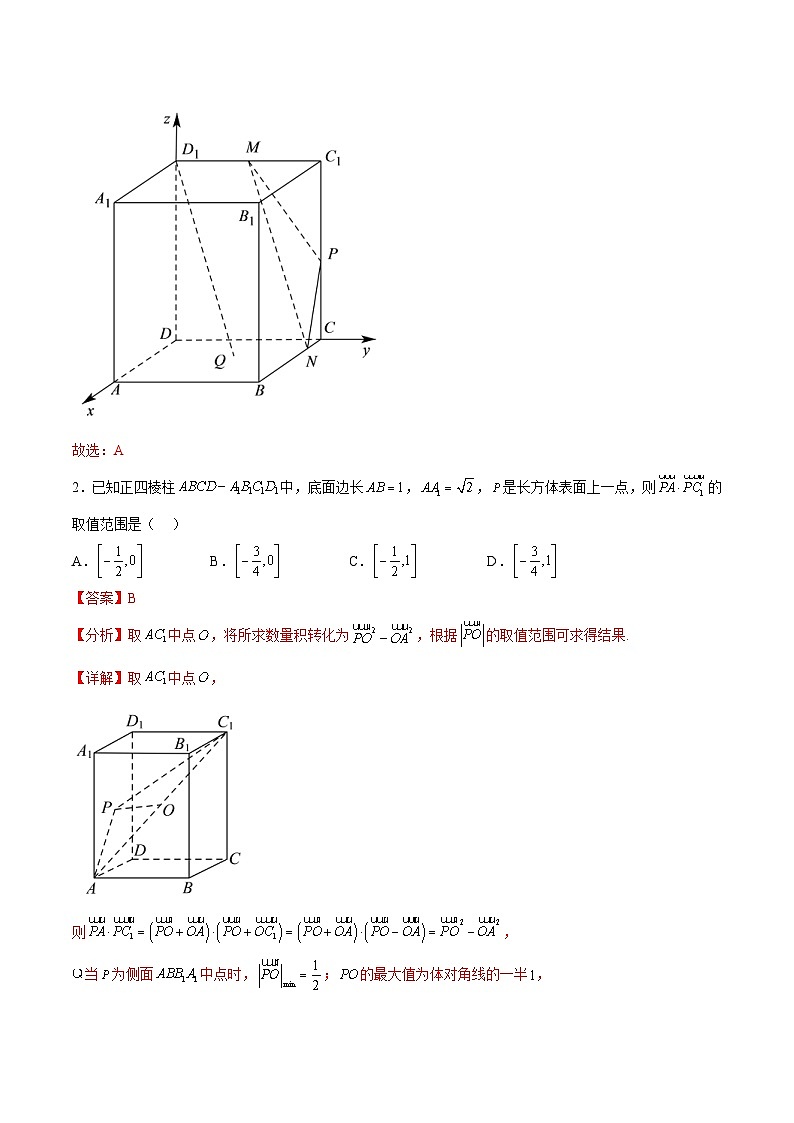
1.在长方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 分别是棱 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 上的点,且 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 是平面 SKIPIF 1 < 0 内一动点,若直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 平行,则 SKIPIF 1 < 0 的最小值为( )
A. SKIPIF 1 < 0 B.17C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.已知正四棱柱 SKIPIF 1 < 0 中,底面边长 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 是长方体表面上一点,则 SKIPIF 1 < 0 的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
3.(多选)已知MN是正方体内切球的一条直径,点 SKIPIF 1 < 0 在正方体表面上运动,正方体的棱长是2,则 SKIPIF 1 < 0 的取值可为( )
A.-1B.0C. SKIPIF 1 < 0 D.5
4.《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.在如图所示的鳖臑 SKIPIF 1 < 0 中, SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,E是BC的中点,H是 SKIPIF 1 < 0 内的动点(含边界),且 SKIPIF 1 < 0 平面ACD,则 SKIPIF 1 < 0 的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
5.(多选)如图,已知正方体 SKIPIF 1 < 0 的棱长为2, SKIPIF 1 < 0 分别是棱 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 是侧面 SKIPIF 1 < 0 内(含边界)的动点,则下列说法正确的是( )
A.若直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 平行,则三棱锥 SKIPIF 1 < 0 的体积为 SKIPIF 1 < 0
B.若直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 平行,则直线 SKIPIF 1 < 0 上存在唯一的点 SKIPIF 1 < 0 ,使得 SKIPIF 1 < 0 与 SKIPIF 1 < 0 始终垂直
C.若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0
D.若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0
6.一个长方体的棱长分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 是该长方体外接球的一条直径,点 SKIPIF 1 < 0 是长方体表面上的一个动点,则 SKIPIF 1 < 0 的取值范围是_____.
7.已知P是棱长为1的正方体 SKIPIF 1 < 0 内(含正方体表面)一动点.
(1)当点P运动到 SKIPIF 1 < 0 中点时, SKIPIF 1 < 0 的值为_____;
(2)当点P运动时, SKIPIF 1 < 0 的最大值为_____.
8.已知球O是棱长为1的正四面体的内切球,AB为球O的一条直径,点P为正四面体表面上的一个动点,则 SKIPIF 1 < 0 的取值范围为_____.
题型二面积、体积的最值范围问题
9.如图,已知四棱锥 SKIPIF 1 < 0 中,正三角形 SKIPIF 1 < 0 的边长为2, SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,则四棱锥 SKIPIF 1 < 0 的体积的最大值为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
10.已知三棱锥 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,三棱锥 SKIPIF 1 < 0 的外接球的表面积为 SKIPIF 1 < 0 ,则三棱锥 SKIPIF 1 < 0 体积的最大值为( )
A.2B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
11.已知底面为矩形的直四棱柱高为4,体积为16,各顶点都在一个球面上,则这个球的体积的最小值是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
12.已知一个圆锥的侧面展开图是半径为4,圆心角为 SKIPIF 1 < 0 的扇形,将该圆锥加工打磨成一个球状零件,则该零件表面积的最大值为_____.
13.如图,在四棱锥 SKIPIF 1 < 0 中,底面 SKIPIF 1 < 0 是平行四边形, SKIPIF 1 < 0 , SKIPIF 1 < 0 .记四面体 SKIPIF 1 < 0 的外接球的球心为 SKIPIF 1 < 0 , SKIPIF 1 < 0 为球 SKIPIF 1 < 0 表面上的一个动点,当 SKIPIF 1 < 0 取最大值时,四面体 SKIPIF 1 < 0 体积的最大值为_____.
14.一个圆锥母线与底面所成的角为 SKIPIF 1 < 0 ,体积为 SKIPIF 1 < 0 ,过圆锥顶点的平面截圆锥,则所得截面面积的最大值为_____.
15.如图,在斜三棱柱 SKIPIF 1 < 0 中, SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 为 SKIPIF 1 < 0 上靠近A的三等分点, SKIPIF 1 < 0 为 SKIPIF 1 < 0 上靠近 SKIPIF 1 < 0 的三等分点.
(1)证明:平面 SKIPIF 1 < 0 //平面 SKIPIF 1 < 0 .
(2)若 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,三棱锥 SKIPIF 1 < 0 的体积为 SKIPIF 1 < 0 ,试写出 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的函数关系式.
(3)在(2)的条件下,当 SKIPIF 1 < 0 为多少时,三棱锥 SKIPIF 1 < 0 的体积取得最大值?并求出最大值.
16.如图,四边形 SKIPIF 1 < 0 是圆柱底面的内接四边形, SKIPIF 1 < 0 是圆柱的母线, SKIPIF 1 < 0 , SKIPIF 1 < 0 是 SKIPIF 1 < 0 上的动点.
(1)求圆柱的侧面积 SKIPIF 1 < 0 ;
(2)求四棱锥 SKIPIF 1 < 0 的体积 SKIPIF 1 < 0 的最大值.
题型三夹角的最值范围问题
17.(多选)如图,在正三棱柱 SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则下列说法正确的是( )
A.当 SKIPIF 1 < 0 且 SKIPIF 1 < 0 时,有 SKIPIF 1 < 0
B.当 SKIPIF 1 < 0 时,三棱锥 SKIPIF 1 < 0 的体积为定值 SKIPIF 1 < 0
C.当 SKIPIF 1 < 0 时,直线 SKIPIF 1 < 0 和 SKIPIF 1 < 0 所成的角的取值为 SKIPIF 1 < 0
D.当 SKIPIF 1 < 0 时,直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值范围是 SKIPIF 1 < 0
18.(多选)如图,在棱长为1的正方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 为面对角线 SKIPIF 1 < 0 上的一个动点(包含端点),则下列选项中正确的有( )
A.三棱锥 SKIPIF 1 < 0 的体积为定值
B.线段 SKIPIF 1 < 0 上存在点 SKIPIF 1 < 0 ,使 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
C.当点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 重合时,二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0
D.设直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角为 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0
19.(多选)在正四棱锥 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则下列结论正确的有( )
A. SKIPIF 1 < 0 的最小值是 SKIPIF 1 < 0
B.当 SKIPIF 1 < 0 时,三棱锥 SKIPIF 1 < 0 的体积为定值
C.当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角可能为 SKIPIF 1 < 0
D.当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角正弦值的最大值为 SKIPIF 1 < 0
20.(多选)在棱长为1的正方体 SKIPIF 1 < 0 中,点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点,点 SKIPIF 1 < 0 , SKIPIF 1 < 0 分别为线段 SKIPIF 1 < 0 , SKIPIF 1 < 0 上的动点,则( )
A. SKIPIF 1 < 0 B.平面 SKIPIF 1 < 0 可能经过顶点 SKIPIF 1 < 0
C. SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 D. SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0
21.如图(1)所示,在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 垂直平分 SKIPIF 1 < 0 .现将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 折起,使得二面角 SKIPIF 1 < 0 大小为 SKIPIF 1 < 0 ,得到如图(2)所示的空间几何体(折叠后点 SKIPIF 1 < 0 记作点 SKIPIF 1 < 0 )
(1)求点 SKIPIF 1 < 0 到面 SKIPIF 1 < 0 的距离;
(2)求四棱锥 SKIPIF 1 < 0 外接球的体积;
(3)点 SKIPIF 1 < 0 为一动点,满足 SKIPIF 1 < 0 ,当直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角最大时,试确定点 SKIPIF 1 < 0 的位置.
22.如图,在三棱台 SKIPIF 1 < 0 中侧面 SKIPIF 1 < 0 为等腰梯形, SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点.底面 SKIPIF 1 < 0 为等腰三角形, SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点.
(1)证明:平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ;
(2)记二面角 SKIPIF 1 < 0 的大小为 SKIPIF 1 < 0 .
①当 SKIPIF 1 < 0 时,求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
②当 SKIPIF 1 < 0 时,求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦的最大值.
23.如图,在三棱锥 SKIPIF 1 < 0 中, SKIPIF 1 < 0 的中点为 SKIPIF 1 < 0 .
(1)证明:直线 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ;
(2)若 SKIPIF 1 < 0 ,当直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角最大时,求三棱锥 SKIPIF 1 < 0 的体积.
24.已知直三棱柱 SKIPIF 1 < 0 中,侧面 SKIPIF 1 < 0 为正方形, SKIPIF 1 < 0 ,E,F分别为AC和 SKIPIF 1 < 0 的中点,D为棱 SKIPIF 1 < 0 上的动点. SKIPIF 1 < 0 .
(1)证明: SKIPIF 1 < 0 ;
(2)求平面 SKIPIF 1 < 0 与平面DEF所成的二面角正弦值的最小值及此时点D的位置.
题型四距离的最值范围问题
25.在长方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,动点P在体对角线 SKIPIF 1 < 0 上,则顶点B到平面APC距离的最大值为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
26.如图,已知正方体 SKIPIF 1 < 0 的棱长为1,则线段 SKIPIF 1 < 0 上的动点P到直线 SKIPIF 1 < 0 的距离的最小值为( )
A.1B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
27.(多选)在长方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,动点 SKIPIF 1 < 0 在体对角线 SKIPIF 1 < 0 上(含端点),则下列结论正确的有( )
A.顶点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的最大距离为 SKIPIF 1 < 0 B.存在点 SKIPIF 1 < 0 ,使得 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
C. SKIPIF 1 < 0 的最小值 SKIPIF 1 < 0 D.当 SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点时, SKIPIF 1 < 0 为钝角
28.(多选)已知正方体 SKIPIF 1 < 0 ,的棱长为2,E为 SKIPIF 1 < 0 的中点,平面 SKIPIF 1 < 0 过B, SKIPIF 1 < 0 ,E三点,则( )
A. SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 平行
B.平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 垂直
C.平面 SKIPIF 1 < 0 截正方体所得截面面积为 SKIPIF 1 < 0
D.正方体的顶点到平面 SKIPIF 1 < 0 的距离最大值 SKIPIF 1 < 0
29.(多选)长方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 上一动点,则 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离不可能是( )
A. SKIPIF 1 < 0
B. SKIPIF 1 < 0
C. SKIPIF 1 < 0
D. SKIPIF 1 < 0
30.如图,在棱长为4的正方体 SKIPIF 1 < 0 中,E为BC的中点,点P在线段 SKIPIF 1 < 0 上,点Р到直线 SKIPIF 1 < 0 的距离的最小值为_____.
31.如图,AB是底面圆O的直径,点C是圆O上异于A、B的点,PO垂直于圆O所在的平面,且 SKIPIF 1 < 0 ,点E在线段PB上,则 SKIPIF 1 < 0 的最小值为_____.
题型一
数量积的最值范围范围
题型二
面积、体积的最值范围问题
题型三
夹角的最值范围问题
题型四
距离的最值范围问题
人教A版高二数学上学期重难点突破期末复习专题1.1 空间向量及其运算(七个重难点突破)(2份打包,原卷版+解析版): 这是一份人教A版高二数学上学期重难点突破期末复习专题1.1 空间向量及其运算(七个重难点突破)(2份打包,原卷版+解析版),文件包含人教A版高二数学上学期重难点突破期末复习专题11空间向量及其运算七个重难点突破原卷版doc、人教A版高二数学上学期重难点突破期末复习专题11空间向量及其运算七个重难点突破解析版doc等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
专题15 圆锥曲线中的范围、最值问题(重难点突破)-2023-2024学年高二数学上学期精品讲义(人教A版): 这是一份专题15 圆锥曲线中的范围、最值问题(重难点突破)-2023-2024学年高二数学上学期精品讲义(人教A版),文件包含专题15圆锥曲线中的范围最值问题重难点突破原卷版-高二数学上学期精品讲义人教A版docx、专题15圆锥曲线中的范围最值问题重难点突破解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
新高考数学一轮复习《高考大题突破练——范围与最值问题》课时练习(2份打包,教师版+原卷版): 这是一份新高考数学一轮复习《高考大题突破练——范围与最值问题》课时练习(2份打包,教师版+原卷版),文件包含新高考数学一轮复习《高考大题突破练范围与最值问题》课时练习教师版doc、新高考数学一轮复习《高考大题突破练范围与最值问题》课时练习原卷版doc等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。












