2024年陕西省安康市高新中学高考数学模拟试卷（文科）（2月份）（含解析）

这是一份2024年陕西省安康市高新中学高考数学模拟试卷（文科）（2月份）（含解析），共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.设集合A={1,3,5,7,9,11}，B={1,3,7}，则∁AB=( )
A. {5,9,11}B. {3,5,9}C. {1,5,9}D. {1,5,9,11}
2.已知复数z满足zi−5=6i，则z的虚部为( )
A. 5B. −5C. 5iD. −5i
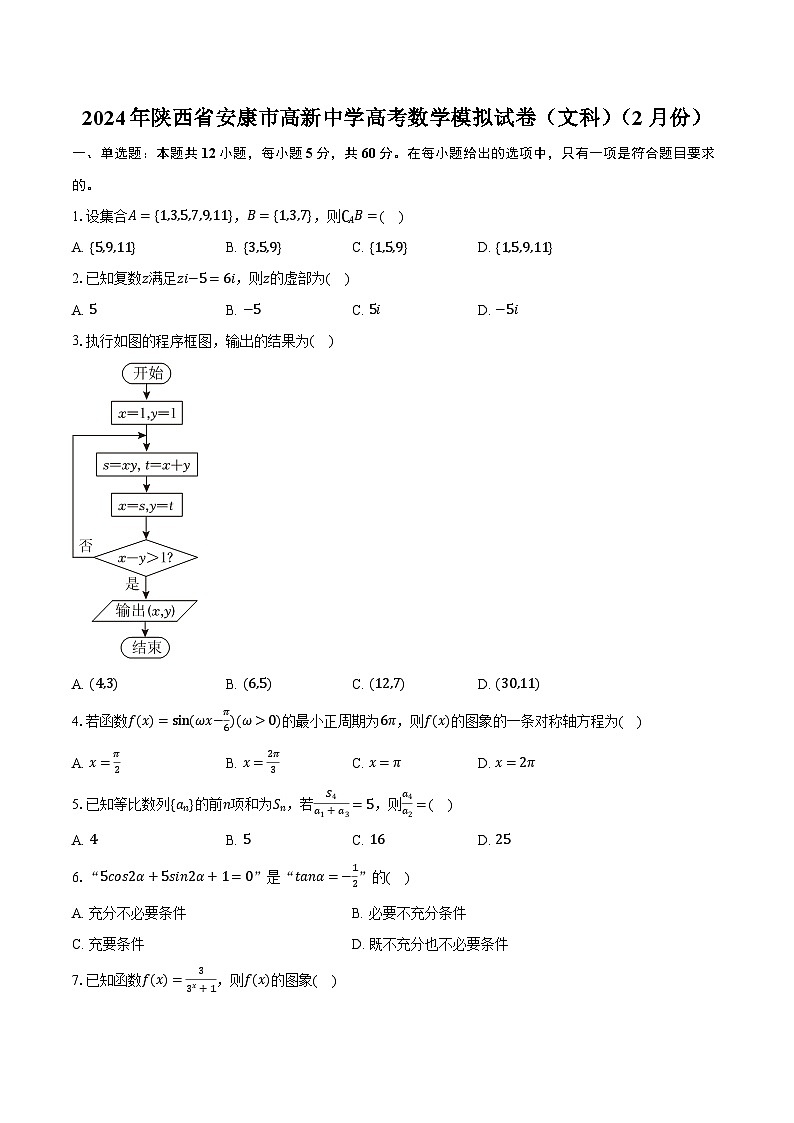
3.执行如图的程序框图，输出的结果为( )
A. (4,3)B. (6,5)C. (12,7)D. (30,11)
4.若函数f(x)=sin(ωx−π6)(ω>0)的最小正周期为6π，则f(x)的图象的一条对称轴方程为( )
A. x=π2B. x=2π3C. x=πD. x=2π
5.已知等比数列{an}的前n项和为Sn，若S4a1+a3=5，则a4a2=( )
A. 4B. 5C. 16D. 25
6.“5cs2α+5sin2α+1=0”是“tanα=−12”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
7.已知函数f(x)=33x+1，则f(x)的图象( )
A. 关于点(32,0)对称B. 关于直线x=32对称
C. 关于点(0,32)对称D. 关于直线x=12对称
8.在区间[0,5]内随机取一个实数a，则关于x的不等式x2+(2−a)x−2a<0仅有2个整数解的概率为( )
A. 25B. 310C. 15D. 110
9.已知正三棱台ABC−A1B1C1中，△A1B1C1的面积为4 3，△ABC的面积为9 3，AA1=2，则该三棱台的体积为( )
A. 38 33B. 38 23C. 193D. 389
10.已知函数f(x)=ex−λ(x2+1)有两个极值点p，q，若q=2p，则f(0)=( )
A. 1−ln22B. 1−2ln2C. 1−ln2D. 1−1ln2
11.已知双曲线C：x2a2−y2b2=1(a>0,b>0)的右焦点为F，过F且与一条渐近线平行的直线与C的右支及另一条渐近线分别交于B，D两点，若FB=BD，则C的渐近线方程为( )
A. y=±2xB. y=± 3xC. y=±xD. y=± 2x
12.已知△ABC中，AB=6，C=π3，若△ABC所在平面内一点D满足DA+DB+12DC=0，则DA⋅DB的最大值为( )
A. −19825B. −9925C. −6625D. −3325
二、填空题：本题共4小题，每小题5分，共20分。
13.已知圆锥的底面半径为1，体积为2 2π3，则该圆锥的侧面展开图对应的扇形的圆心角为______．
14.已知数列{an}中，a1=1，且an+1(an+1)+1=0，则{an}的前12项和为______．
15.小明的生日是12月23日，他从1，2，2，3这四个数字的所有不同排列中任选一种设置为自己的4位数手机密码，则他设置的密码中1与3相邻的概率为______．
16.已知抛物线C：y2=2px(p>0)的焦点为F，准线l：x=−12，直线l′过点F且与抛物线C交于M，N两点，O为坐标原点，若|MF||NF|=34，则△OMN的面积为______．
三、解答题：本题共7小题，共82分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题12分)
已知△ABC中，角A，B，C所对的边分别为a，b，c，且sinBsinA+sinAsinB−4csC=0．
(1)证明：a2+b2=2c2；
(2)若csB=sin2BsinAsinC，求csA的值．
18.(本小题12分)
为了适应当代年轻人的生活需求，某餐厅推出了一款套餐，现随机抽取了10位顾客请他们对这款套餐进行评分，所得数据为84，85，88，89，92，93，93，95，95，96，规定评分大于90为“满意”．
(Ⅰ)求这10位顾客评分的平均数以及方差；
(Ⅱ)为了解不同性别的顾客对这款套餐的看法，餐厅又随机抽取了100位顾客进行调查，已知这100位顾客的满意率与第一次抽取的10位顾客的满意率相等，完成下面的2×2列联表，并判断：是否有99%的把握认为不同性别的顾客对这款套餐的满意程度有差异？
附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)．
19.(本小题12分)
如图所示，在直三棱柱ABC−A1B1C1中，AA1=6，BC=4，∠ABC=∠ACB，D为棱BC的中点，E为棱BB1上靠近B1的三等分点，F为线段AD上的动点．
(Ⅰ)求证：C1E⊥平面DEF；
(Ⅱ)若四面体C1DEF的体积为203，求∠EFD的正弦值．
20.(本小题12分)
记函数f(x)的导函数为f′(x)，f′(x)的导函数为f′′(x)，设D是f(x)的定义域的子集，若在区间D上f′′(x)≤0，则称f(x)在D上是“凸函数”.已知函数f(x)=asinx−x2．
(Ⅰ)若f(x)在[0,π2]上为“凸函数”，求a的取值范围；
(Ⅱ)若a=2，判断g(x)=f(x)+1在区间(0,π)上的零点个数．
21.(本小题12分)
已知椭圆C：x2a2+y2b2=1(a>b>0)的离心率为 32，直线l过C的上顶点与右顶点且与圆O：x2+y2=45相切．
(1)求C的方程．
(2)过C上一点A(x0,y0)作圆O的两条切线l1，l2(均不与坐标轴垂直)，l1，l2与C的另一个交点分别为M(x1,y1)，N(x2,y2).证明：
①直线AM，AN的斜率之积为定值；
②x1+x2=0．
22.(本小题10分)
已知平面直角坐标系xOy中，直线l过坐标原点且倾斜角为α.以坐标原点为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ2−4ρsin(θ+π6)+1=0．
(Ⅰ)求l的极坐标方程以及C的直角坐标方程；
(Ⅱ)若α∈(0,π2)，l与C交于M，N两点，设|OM|+|ON|=λ|OM||ON|，求λ的最大值．
23.(本小题12分)
已知函数f(x)=|x+m|+|2x−3|．
(Ⅰ)若m=2，求不等式f(x)>10的解集；
(Ⅱ)若对任意x≥3，不等式f(x)≤x2恒成立，求实数m的取值范围．
答案和解析
1.【答案】A
【解析】解：集合A={1,3,5,7,9,11}，B={1,3,7}，
则∁AB={5,9,11}．
故选：A．
利用补集定义能求出结果．
本题考查补集定义等基础知识，考查运算求解能力，是基础题．
2.【答案】B
【解析】解：由题意可得：z=5+6ii=6−5i，
所以z的虚部为−5．
故选：B．
根据复数的除法运算求z，进而可得结果．
本题主要考查了复数的四则运算及复数的基本概念，属于基础题．
3.【答案】D
【解析】解：第一次循环：s=1×1=1，t=1+1=2，x=1，y=2，x−y=−1，不满足x−y>1，循环继续，
第二次循环：s=1×2=2，t=1+2=3，x=2，y=3，x−y=−1，不满足x−y>1，循环继续，
第三次循环：s=2×3=6，t=2+3=5，x=6，y=5，x−y=1，不满足x−y>1，循环继续，
第四次循环：s=6×5=30，t=6+5=11，x=30，y=11，x−y=19，满足x−y=1，跳出循环，
故输出的结果为(30,11)．
故选：D．
根据程序框图，依次求出每次循环，即可求解．
本题主要考查程序框图的应用，属于基础题．
4.【答案】D
【解析】解：由题意可得函数的周期为T=2πω=6π，则ω=13，
所以f(x)=sin(13x−π6)，
令13x−π6=π2+kπ,k∈Z，解得x=2π+3kπ，k∈Z，故D正确．
故选：D．
利用周期求出ω的值，再根据正弦函数的对称性即可求解．
本题考查了正弦函数的对称性，属于基础题．
5.【答案】C
【解析】解：设等比数列{an}的公比为q，
由S4a1+a3=a1+a2+a3+a4a1+a3=a1+a3+(a1+a3)qa1+a3=1+q=5，得q=4，
所以a4a2=q2=16．
故选：C．
根据a2+a4=(a1+a3)q可得S4a1+a3=1+q=5，从而q=4，进一步根据a4a2=q2进行求解即可．
本题考查等比数列的性质，考查学生归纳推理与数学运算的能力，属于基础题．
6.【答案】B
【解析】解：5cs2α+5sin2α+1=0⇔5(cs2α−sin2α)+10sinαcsα+cs2α+sin2α=0
⇔3cs2α−2sin2α+5sinαcsα=0，
显然csα≠0，则2tan2α−5tanα−3=0，解得tanα=−12或tanα=3．
所以“5cs2α+5sin2α+1=0”是“tanα=−12”的必要不充分条件．
故选：B．
利用三角恒等变换得到tanα=−12或tanα=3，从而得到答案．
本题主要考查了二倍角公式及同角基本关系的应用，属于中档题．
7.【答案】C
【解析】解：因为f(1)=34，f(2)=310，f(1)≠±f(2)，即函数的图象不关于(32,0)对称，也不关于x=32对称，A，B错误；
因为f(−x)+f(x)=31+3−x+31+3x=3⋅3x1+3x+31+3x=3，即f(x)的图象关于(0,32)对称，C正确；
因为f(0)=32，f(0)≠±f(1)，即函数的图象不关于x=12对称，D错误．
故选：C．
根据函数的对称性检验各选项即可判断．
本题主要考查了函数对称性的判断，属于基础题．
8.【答案】C
【解析】解：根据题意，x2+(2−a)x−2a<0⇔−2由于a∈[0,5]，且不等式x2+(2−a)x−2a<0仅有2个整数解，
必有0故要求概率P=15．
故选：C．
根据题意，求出不等式的解集，分析a的取值范围，结合几何概型计算公式分析可得答案．
本题考查几何概型的计算，涉及二次不等式的解法，属于基础题．
9.【答案】B
【解析】解：正三棱台ABC−A1B1C1中，△A1B1C1的面积为4 3，△ABC的面积为9 3，AA1=2，
∴S△A1B1C1=12×A1B12×sinπ3=4 3，解得A1B1=4，
S△ABC=12×AB2×sinπ3=9 3，解得AB=6，
设O，O1分别是△ABC，△A1B1C1的中心，
设D，D1分别是BC，B1C1的中点，
∴A，O，D三点共线，A1，O1，D1三点共线，
AD=6×sinπ3=3 3，A1D1=4sinπ3=2 3，
∴OD=13AD= 3，O1D1=13A1D1=2 33，
DD1= BB12−(BC−B1C12)2= 22−(6−42)2= 3，
过D1作D1E⊥AD，垂足为E，则D1E//OO1，
∵D1E= DD12−DE2= ( 3)2−( 3−2 33)2=2 63，
∴三棱台的高为2 63，
∴三棱台的体积为V=13×2 63×(4 3+ 4 3×9 3+9 3)=38 23．
故选：B．
先计算出三棱台的高，进而计算出三棱台的体积．
本题考查正三棱台结构特征、体积公式、线面垂直等基础知识，考查运算求解能力，是中档题．
10.【答案】D
【解析】解：依题意，f′(x)=ex−2λx，
则ep−2λp=0eq−2λq=0，
因为q=2p，所以ep=2λpe2p=4λp，
显然λ，p≠0，两式相除得ep=2，则p=ln2，
代入ep=2λp中，解得λ=1ln2，则f(0)=1−1ln2．
故选：D．
求导，得到方程组，求出p=ln2，进而得到λ=1ln2，得到答案．
本题主要考查了导数与单调性及极值关系的应用，属于基础题．
11.【答案】C
【解析】解：易知C的渐近线方程为y=±bax，不妨设直线BD：y=ba(x−c)，B(x1,y1)，D(x2,y2)，
联立方程得y=ba(x−c)y=−bax，解得x2=c2，y2=−bc2a，所以D(c2,−bc2a)，
又FB=BD，而FB=(x1−c,y1)，BD=(c2−x1,−bc2a−y1)，得到x1−c=c2−x1y1=−bc2a−y1，
解得x1=34c,y1=−bc4a，故B(3c4,−bc4a)，代入x2a2−y2b2=1中，
得9c216a2−c216a2=1，得到c2a2=2，又c2=a2+b2，得到b2a2=1，解得ba=1，
故所求C的渐近线方程为y=±x．
故选：C．
设直线BD：y=ba(x−c)，B(x1,y1)，D(x2,y2)，由y=ba(x−c)y=−bax得到D(c2,−bc2a)，再根据条件得出B(3c4,−bc4a)，代入方程x2a2−y2b2=1，即可求出结果．
本题考查双曲线的简单性质的应用，渐近线方程的求法，考查数形结合以及计算能力，是中档题．
12.【答案】A
【解析】解：设AB的中点为E，△ABC的三条边分别为a、b、c，则DA+DB=2DE，
因为DA+DB+12DC=0，所以DA+DB=−12DC=12CD，
所以2DE=12CD，即DE=14CD，所以D是DE靠近E的五等分点，如图所示：
则DA⋅DB=(CD−CA)⋅(CD−CB)
=CD2−CD⋅CB−CD⋅CA+CA⋅CB
=(45CE)2−45CE⋅(CA+CB)+CA⋅CB
=1625×14(CA+CB)2−45×12(CA+CB)⋅(CA+CB)+CA⋅CB
=−625(CA2+CB2)+1325CA⋅CB
=−625(b2+a2)+1325×bacsπ3
=−625(a2+b2)+1350ab，
由余弦定理得，c2=a2+b2−2abcsC=a2+b2−ab=36，
由基本不等式得：36=a2+b2−ab≥2ab−ab=ab，所以ab≤36，当且仅当a=b时取“=”，
所以−625(a2+b2)+1350ab=−625×(36+ab)+1350ab=−21625+150ab≤−21625+150×36=−19825，
所以DA⋅DB的最大值为−19825．
故选：A．
设AB的中点为E，△ABC的三条边分别为a、b、c，由中线的向量表示，结合题意得出D是DE靠近E的五等分点，根据余弦定理和基本不等式，即可求出DA⋅DB的最大值．
本题考查了平面向量的数量积运算问题，也考查了运算求解能力，是中档题．
13.【答案】2π3
【解析】解：设圆锥(如图所示)的高为h，
因为13⋅π⋅12⋅h=2 2π3，
所以h=2 2，母线SA= 12+(2 2)2=3，
将圆锥沿SA展开所得扇形的弧长为底面周长2π，根据弧长公式α⋅SA=2π，
所以圆心角α=2π3．
故答案为：2π3．
根据体积先计算出圆锥的高，再根据高计算出圆锥的母线，即展开图扇形的半径，最后再根据弧长公式求出圆心角．
本题主要考查了圆锥的结构特征，属于基础题．
14.【答案】−6
【解析】解：依题意an≠−1，故an+1=−1an+1，a1=1，
所以a2=−12，a3=−2，a4=1，…，
故{an}的前12项和为(1−12−2)×4=−6．
故答案为：−6．
由已知可得an+1=−1an+1，借助数列的周期性、分组求和即可得出结果．
本题考查的知识要点：数列的递推关系式，数列的求和，主要考查学生的运算能力，属于基础题．
15.【答案】12
【解析】解：1，2，2，3这四个数字的所有不同排列有A44A22=12种，
其中1与3相邻的有1322，3122，2132，2312，2213，2231，共6种，
所以所求概率为612=12．
故答案为：12．
利用古典概型的概率公式求解．
本题主要考查了古典概型的概率公式，属于基础题．
16.【答案】7 324
【解析】解：∵抛物线C：y2=2px(p>0)的焦点为F，准线l：x=−12，设M(x1,y1)，N(x2,y2)，且y1>0，y2<0，
可得p2=12，即p=1，
∴抛物线C：y2=2x，焦点坐标为(12,0)，
由题可设直线MN的方程为x=my+12，
∵|MF||NF|=34，
∴|y1||y2|=34，可得y1=−34y2，①
联立：x=my+12y2=2x，整理可得y2−2my−1=0，
Δ=(−2m)2+4>0，
∴y1+y2=2m，②y1⋅y2=−1，③
联立①③可得：y1= 32，y2=−2 33，
∵△OMN的面积S=12|OF|×|y1−y2|=12×12×7 36=7 324．
故答案为：7 324．
根据已知求得p=1，设直线MN的方程为x=my+12，联立：x=my+12y2=2x，结合已知条件即可求得结论．
本题考查抛物线的简单性质，考查直线与抛物线位置关系的应用，考查计算能力，是中档题．
17.【答案】(1)证明：由正弦定理及条件可得ba+ab−4csC=0，
由余弦定理可得b2+a2ab−4⋅a2+b2−c22ab=0，
整理可证得：a2+b2=2c2；
(2)解：由csB=sin2BsinAsinC得a2+c2−b22ac=b2ac，
化简得a2+c2=3b2，又a2+b2=2c2，故b= 32c，
所以a= 52c，
故csA=b2+c2−a22bc= 36．
【解析】(1)由题意及正弦定理，余弦定理可证得结论；
(2)由余弦定理及(1)可得a，b，c之间的关系，进而可得csA的值．
本题考查正弦定理及余弦定理的应用，属于中档题．
18.【答案】解：(Ⅰ)平均数为84+85+88+89+92+93+93+95+95+9610=91，
方差为(84−91)2+(85−91)2+(88−91)2+(89−91)2+(92−91)2+(93−91)2+(93−91)2+(95−91)2+(95−91)2+(96−91)210=16.4；
(Ⅱ)由题意可知，第一次抽取的10位顾客的满意率为610=35，
所以100位顾客中评分为满意的人数为100×35=60人，
补全2×2列联表，如下：
所以K2=100×(40×30−20×10)260×40×50×50≈16.667>6.635，
所以有99%的把握认为不同性别的顾客对这款套餐的满意程度有差异．
【解析】(Ⅰ)利用平均数和方差的定义求解；
(Ⅱ)根据第一次抽取的10位顾客的满意率求出100位顾客中评分为满意的人数，填写2×2列联表，计算K2，对照题目中的表格，得出统计结论．
本题主要考查了平均数和方差的定义，考查了独立性检验的应用，属于中档题．
19.【答案】解：(Ⅰ)证明：∵∠ABC=∠ACB，∴AB=AC，
∵D是BC的中点，∴AD⊥BC，
∵CC1⊥平面ABC，AD⊂平面BCC1D1，∴CC1⊥AD，
∵BC∩CC1=C，∴AD⊥平面BCC1B1，
∵C1E⊂平面BCC1C1，∴AD⊥C1E，
由题设知B1E=2，BE=4，C1E=DE=2 5，C1D=2 10，
∴C1E2+DE2=C1D2，∴C1E⊥DE，
∵AD∩DE=D，∴C1E⊥平面DEF．
(Ⅱ)由(Ⅰ)得AD⊥平面BCC1B1，∴DF⊥平面BCC1B1，
VC1−DEF=VF−C1DE=13(12×2 5×2 5)×DF=203，解得DF=2，
∵DE⊂平面BCC1B1，∴DF⊥DE，
∴EF= 22+(2 5)2=2 6，
∴sin∠EFD=2 52 6= 306．
【解析】(Ⅰ)通过证明C1E⊥DE，AD⊥C1E来证明C1E⊥平面DEF；
(Ⅱ)根据四面体C1DEF的体积求出DF，进而求出∠EFD的正弦值．
本题考查线面垂直的判定与性质、勾股定理等基础知识，考查运算求解能力，是中档题．
20.【答案】解：(Ⅰ)由f(x)=asinx−x2可得其定义域为R，且f′(x)=acsx−2x，
所以f″(x)=−asinx−2，
若f(x)在[0,π2]上为“凸函数”可得f″(x)=−asinx−2≤0在[0,π2]恒成立，
当a≥0时，显然符合题意；
当a<0时，需满足−asinπ2−2≤0，可得−2≤a<0；
综上可得a的取值范围为[−2,+∞)；
(Ⅱ)若a=2，可得g(x)=2sinx−x2+1，所以g′(x)=2csx−2x，
令h(x)=2csx−2x，则h′(x)=−2sinx−2；
易知h′(x)=−2sinx−2<0在区间(0,π)上恒成立，
因此可得h(x)=g′(x)=2csx−2x在(0,π)上单调递减；
显然g′(π6)=2csπ6−2×π6= 3−π3>0，
g′(π4)=2csπ4−2×π4= 2−π2<0，
根据零点存在定理可得存在x0∈(π6,π4)使得g′(x0)=2csx0−2x0=0，
因此可知当x∈(0,x0)时，g′(x)>0，即g(x)在(0,x0)上为单调递增；
当x∈(x0,π)时，g′(x)<0，即g(x)在(x0,π)上为单调递减；
又g(0)=2sin0−02+1=1，显然在(0,x0)上g(x)不存在零点；
而g(π)=2sinπ−π2+1=1−π2<0，结合单调性可得在(x0,π)上g(x)存在一个零点；
综上可知，g(x)=f(x)+1在区间(0,π)上仅有1个零点．
【解析】(Ⅰ)根据“凸函数”定义对函数求导，由不等式−asinx−2≤0在[0,π2]恒成立即可求得a的取值范围；
(Ⅱ)易知g(x)=2sinx−x2+1，由导函数求得其在(0,π)上的单调性，利用零点存在定理可知零点个数为1个．
本题主要考查利用导数研究函数的单调性，函数零点个数问题，考查运算求解能力，属于难题．
21.【答案】(1)解：设椭圆的半焦距为c(c>0)，
依题意，离心率e=ca= 1−b2a2= 32，
所以a=2b，c= 3b，
直线l：xa+yb=1，即bx+ay−ab=0，
因为直线l与圆O相切，所以ab a2+b2=2 5，
解得a=2，b=1，
故C的方程为x24+y2=1．

(2)证明：①设过点A且与圆O相切的直线的方程为y−y0=k(x−x0)(k≠0)，
则|kx0−y0| 1+k2=2 5，整理得(5x02−4)k2−10x0y0k+5y02−4=0，
记直线AM，AN的斜率分别为k1，k2，则k1k2=5y02−45x02−4=5(1−x024)−45x02−4=−14，为定值．
②由①可知直线AM：y−y0=k1(x−x0)，
联立y−y0=k1(x−x0),x2+4y2−4=0,则有(1+4k12)x2+8k1(y0−k1x0)x+4(y0−k1x0)2−4=0，
所以x1+x0=8k1(k1x0−y0)1+4k12，
直线AN：y−y0=k2(x−x0)，
同理可得x2+x0=8k2(k2x0−y0)1+4k22，
所以x1+x0+x2+x0=8k1(k1x0−y0)1+4k12+8k2(k2x0−y0)1+4k22=8k1(k1x0−y0)1+4k12+8(−14k1)(−14k1x0−y0)1+4(−14k1)2
=8k12x0−8k1y01+4k12+2x0+8k1y01+4k12=2x0+8k12x01+4k12=2x0，
故x1+x2=0．
【解析】(1)结合椭圆的几何性质与点到直线的距离公式，求出a和b的值，即可得椭圆方程；
(2)①利用点到直线的距离可得切线斜率满足的方程，结合韦达定理，求证斜率之积为定值即可； ②分别联立直线AM、AN与椭圆的方程，结合韦达定理求证即可．
本题考查直线与椭圆的位置关系，熟练掌握椭圆的几何性质，点到直线的距离公式，直线的方程等是解题的关键，考查逻辑推理能力和运算能力，属于中档题．
22.【答案】解：(Ⅰ)直线l过坐标原点且倾斜角为α.转换为极坐标方程θ=α；
曲线C的极坐标方程为ρ2−4ρsin(θ+π6)+1=0，根据x=ρcsθy=ρsinθx2+y2=ρ2，转换为直角坐标方程为x2+y2−2x−2 3y+1=0．
(Ⅱ)直线l的参数方程为x=tcsαy=tsinα(t为参数)，代入x2+y2−2x−2 3y+1=0，
得到t2−(2csα+2 3sinα)t+1=0；
所以t1+t2=2csα+2 3sinα，t1t2=1；
所以λ=|OM|+|ON||OM||ON|=2csα+2 3sinα=4sin(α+π6)，
由于α∈(0,π2)，故α+π6∈(π6,2π3)，
当α+π6=π2时，λ的最大值为4．
【解析】(Ⅰ)直接利用转换关系，把直线的方程转换为极坐标方程，再把曲线的极坐标方程转换为直角坐标方程；
(Ⅱ)利用直线和曲线的位置关系，根据一元二次方程根和系数的关系求出结果．
本题考查的知识要点：参数方程，极坐标方程和直角坐标方程之间的转换，一元二次方程根和系数的关系的应用，主要考查学生的运算能力，属于中档题．
23.【答案】解：(Ⅰ)当m=2时，f(x)=|x+2|+|2x−3|；
若x<−2，则f(x)=−x−2+3−2x=1−3x；
不等式f(x)>10等价于1−3x>10，解得x<−3；
此时不等式的解集为{x|x<−3}；
若−2≤x≤32，则f(x)=x+2+3−2x=5−x；
不等式f(x)>10等价于5−x>10，解得x<−5；
此时不等式的解集为⌀；
若x>32，则f(x)=x+2+2x−3=3x−1；
不等式f(x)>10等价于3x−1>10，解得x>113；
此时不等式的解集为{x|x>113}；
综上，不等式f(x)>10的解集为(−∞,−3)∪(113,+∞)．
(Ⅱ)若x≥3，可得f(x)=|x+m|+2x−3，
不等式f(x)≤x2恒成立等价于|x+m|+2x−3≤x2，即|x+m|≤x2−2x+3；
所以−x2+2x−3≤x+m≤x2−2x+3，即−x2+x−3≤m≤x2−3x+3对任意x≥3恒成立，
利用二次函数单调性可得y=x2−3x+3在[3,+∞)上单调递增，其最小值为3，
函数y=−x2+x−3在[3,+∞)上单调递减，其最大值为−9，所以−9≤m≤3．
所以实数m的取值范围为[−9,3]．
【解析】(Ⅰ)利用分类讨论法分别求出不等式f(x)>10在不同取值范围时的解集即可；
(Ⅱ)根据题意将不等式恒成立问题转化为求二次函数最值，即可得实数m的取值范围．
本题考查了绝对值三角不等式的解法，利用不等式恒成立求参数的取值范围，考查了分类讨论思想和转化思想，属中档题．满意
不满意
总计
男性顾客
40
10
50
女性顾客
50
总计
100
P(K2≥k0)
0.1
0.05
0.01
0.001
k0
2.706
3.841
6.635
10.828
满意
不满意
总计
男性顾客
40
10
50
女性顾客
20
30
50
总计
60
40
100