江苏省盐城市2023-2024学年七年级（下）数学第一次月考备考卷

这是一份江苏省盐城市2023-2024学年七年级（下）数学第一次月考备考卷，文件包含考试卷docx、解答卷docx、答题卡pdf等3份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

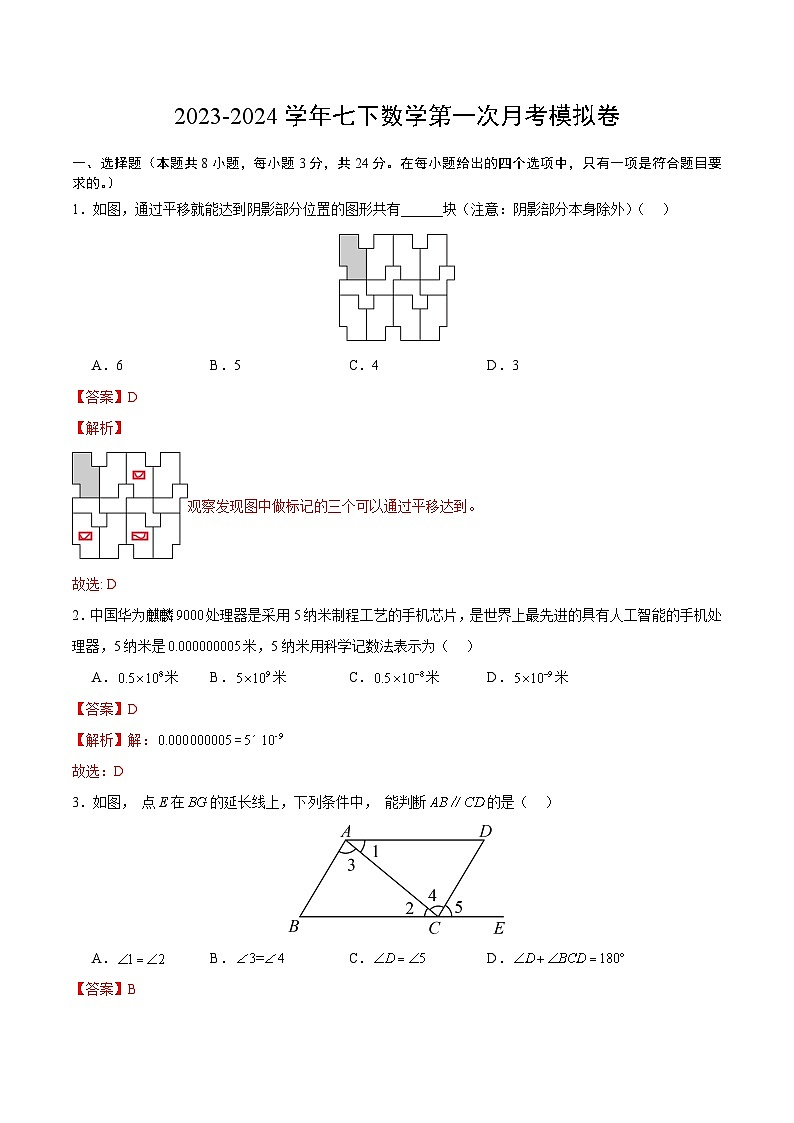
1．如图，通过平移就能达到阴影部分位置的图形共有______块（注意：阴影部分本身除外）（ ）
A．6B．5C．4D．3
【答案】D
【解析】
观察发现图中做标记的三个可以通过平移达到。
故选: D
2．中国华为麒麟处理器是采用5纳米制程工艺的手机芯片，是世界上最先进的具有人工智能的手机处理器，5纳米是米，5纳米用科学记数法表示为（ ）
A．米B．米C．米D．米
【答案】D
【解析】解：
故选：D
3．如图， 点E在的延长线上，下列条件中， 能判断的是（ ）
A．B．C．D．
【答案】B
【解析】解：由，可得，不能判断，故A不符合要求；
由，可得，故B符合要求；
由，可得，不能判断，故C不符合要求；
由，可得，不能判断，故D不符合要求；
故选：B．
4．如图，下面的四个盒子中，每个盒子里都有两根小棒，把其中的一根小棒用剪刀按图中所示的位置剪成两段，这两段小棒再与另一根小棒首尾相接，能够围成一个三角形的是（ ）
A．B．C．D．
【答案】B
【解析】解：图中小棒被剪刀剪成两段，这两段加起来比下面那根木棒短，不符合三角形的三边关系，无法围成三角形；
图中小棒被剪刀剪成两段，这两段加起来比下面那根木棒长，这两段相减比下面那根木棒短，符合三角形的三边关系，可以围成三角形；
图中小棒被剪刀剪成两段，这两段相减比下面那根木棒还长，不符合三角形的三边关系，无法围成三角形；
图中小棒被剪刀剪成两段，这两段加起来和下面那根木棒相等，不符合三角形的三边关系，无法围成三角形．
故选：B．
5．下列计算中正确的是（ ）
A． B．
C．D．
【答案】B
【解析】解：A．，故原式不正确；
B．，正确；
C．，故原式不正确；
D．，故原式不正确；
故选B．
6．已知，，，则这三个数按从小到大的顺序排列为（ ）
A．B．C．D．
【答案】C
【解析】解：∵，，
∴，，
∵，
∴，
故选：C．
7．如图，，，设，，则与之间的数量关系正确的是（ ）
A．B．
C．D．与没有数量关系
【答案】A
【解析】解：过C作∥，
∥，
，
，，
，
，
，
，
，
故选：A．
8．当三角形中一个内角是另外一个内角的时，我们称此三角形为“友好三角形”．如果“一个友好三角形”中有一个内角为，那么这个“友好三角形”的“友好角”的度数为（ ）
A．或B．或C．或或D．或或
【答案】C
【解析】解：①当就是“友好角”时，；
②当时，则，
；
③当既不是也不是时，
则，
，
解得；
综上所述：这个“友好三角形”的“友好角”的度数为或或．
故选：C．
二、填空题：本题共8小题，每小题3分，共24分。
9．计算
【答案】
【解析】解：
，
故答案为：．
10．若，，则 ．
【答案】
【解析】解：
；
故答案为：．
11．已知一个三角形两个内角的度数分别为和，则这个三角形按角进行分类应该为 ．
【答案】钝角三角形
【解析】解：∵一个三角形两个内角的度数分别为和，
∴这个三角形的另外一个内角的度数为，
∵，
∴这个三角形是钝角三角形，
故答案为：钝角三角形．
12．计算 ．
【答案】
【解析】．
故答案为：.
13．一节数学实践课上，老师让同学们用两个大小、形状都相同的三角板画平行线、，并要说出自己做法的依据．小奇、小妙两位同学的做法如图：小奇说：“我做法的依据是：同位角相等，两直线平行．”则小妙做法的依据是 ．
【答案】内错角相等，两直线平行
【解析】解：∵根据题意，，
∴，依据为：内错角相等，两直线平行
故答案为：内错角相等，两直线平行．
14．如图，三角形中，，将三角形沿方向移动至三角形，此时测得，，则阴影部分的面积为 ．
【答案】18
【解析】解：根据平移的性质可得：，，
∴，即，
∵，
∴,
∴．
故答案为：18．
15．如图，将等腰三角形剪去顶角后，得到一个四边形，若，则 ．
【答案】40
【解析】解：根据四边形的内角和定理可得，．
根据三角形的内角和得：．
故答案为：40．
16．如图，直线，点E，F分别在直线，上，点P为直线与间一动点，连接，，且，的平分线与的平分线交于点Q，则的度数为 ．
【答案】或
【解析】解：分两种情况讨论：
①如图1，过点，分别作，，
，
．
，．
．
的平分线与的平分线交于点，
，．
，
，
同理可得；
②如图2，过点，分别作，，
，
．
，．
，
．
的平分线与的平分线交于点，
，．
．
，同①可得．

综上所述，的度数为或．
故答案为：或
三、解答题：本题共9小题，共72分。解答应写出文字说明、证明过程或演算步棸。
17．（12分）计算：
(1)；
(2)；
(3)；
(4)．
【解析】（1）解：
；
（2）解：
；
（3）解：
；
（4）解：
．
18．（6分）（1）已知，，用含有，的代数式表示
（2）已知，求的值
【解析】（1）解：∵，，
∴；
（2）解：∵，
∴
∴
．
19．（6分）如图，在四边形中，已知，平分，，且．
(1)求的度数．
(2)求的度数．
【解析】（1）解：，，
，
，
平分，
；
（2）解：，
，
，
，
．
20．（6分）如图，在方格纸内将水平向右平移4个单位得到．
(1)画出；
(2)若连接，，则这两条线段之间的关系是______；
(3)画出边上的中线（利用网格点和直尺画图）
【解析】（1）解：如图所示：即为所求；
（2）解：由图可知， ，，
故答案为： ，；
（3）解：如图所示：即为所求；

21．（6分）如图，已知：，
(1)过点A画直线，使；并写出图中相等的角．
(2)你发现：______，说明理由．
【解析】（1）如图，，
∴；
（2），理由：
∵，
∴，
∵，
∴，
故答案为：
22．（6分）请将下列证明过程补充完整：
已知：如图，平分，平分，且
求证：．
证明：∵平分，
∴．
∵平分（已知），
∴______（角的平分线的定义）．
∴（______）．
即．
∵（已知），
∴______（______）．
∴（______）．
【解析】证明：∵平分 （已知），
∴ （角平分线的定义）．
∵平分（已知），
∴（角的平分线的定义）．
∴（等式性质）．
即．
∵（已知），
∴ （等量代换）．
∴（同旁内角互补，两直线平行）．
故答案为：角平分线的定义，，等式性质，，等量代换，同旁内角互补，两直线平行．
23．（6分）观察下列解题过程：计算：的值．
解：设，①
则．②
②-①，得，．
通过阅读，你一定学会了一种解决问题的方法，请用你学到的方法计算：
【解析】，①
则，②
②①，得
∴
∴．
24．（10分）如图，已知，，．
(1)求的度数；
(2)若，判断与的位置关系，并说明理由．
【解析】（1）解：如图，的延长线交于点，
，，
，
，
，
；
（2）证明：，理由如下：
如图，延长交于点，
由（1）知，，
，
，
．
25．（14分）问题情境：如图1，，，，求度数．
小明的思路是：过作，通过平行线性质来求．
(1)按小明的思路，易求得的度数为______度；（直接写出答案）
(2)问题迁移：如图2，，点在射线上运动，记，，当点在、两点之间运动时，问与、之间有何数量关系？请说明理由；
(3)在（2）的条件下，如果点在、两点外侧运动时（点与点、、三点不重合），请直接写出与、之间的数量关系．
【解析】（1）解：过点作，
，
，
，，
，，
，，
．
故答案为：；
（2），
理由：如图，过点作，交于，

，
，
，，
；
（3）当在延长线上时，如图所示，

由（2）可知，，
，
当在延长线上时，如图所示，

由（2）可知，，
.