北师大版八年级下册3 三角形的中位线背景图ppt课件

这是一份北师大版八年级下册3 三角形的中位线背景图ppt课件，共23页。PPT课件主要包含了新知讲解，问题2，两条线段的关系，位置关系，数量关系，DE与BC的关系，DE∥BC，DEBC，猜一猜，你能验证你的猜想吗等内容，欢迎下载使用。
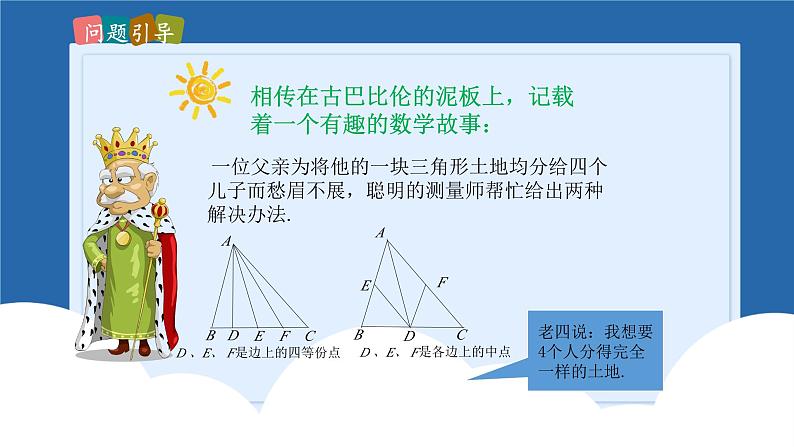
一位父亲为将他的一块三角形土地均分给四个儿子而愁眉不展，聪明的测量师帮忙给出两种解决办法.
相传在古巴比伦的泥板上，记载着一个有趣的数学故事：
老四说：我想要4个人分得完全一样的土地.
D 、E、 F是边上的四等份点
D 、E、 F是各边上的中点
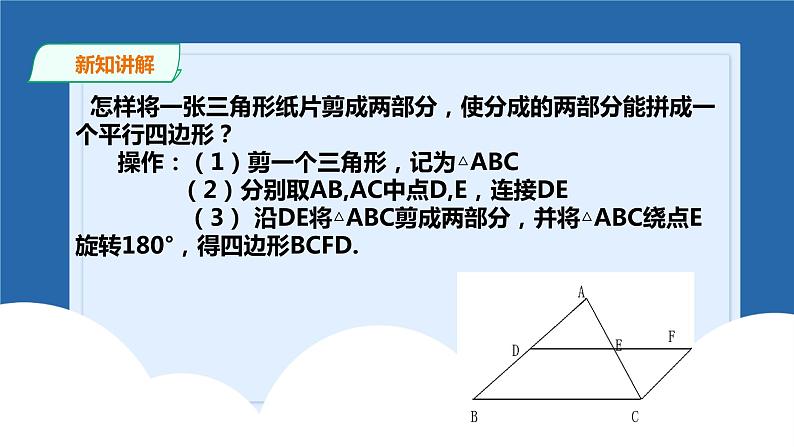
怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？ 操作：（1）剪一个三角形，记为△ABC （2）分别取AB,AC中点D,E，连接DE （3） 沿DE将△ABC剪成两部分，并将△ABC绕点E旋转180°，得四边形BCFD.
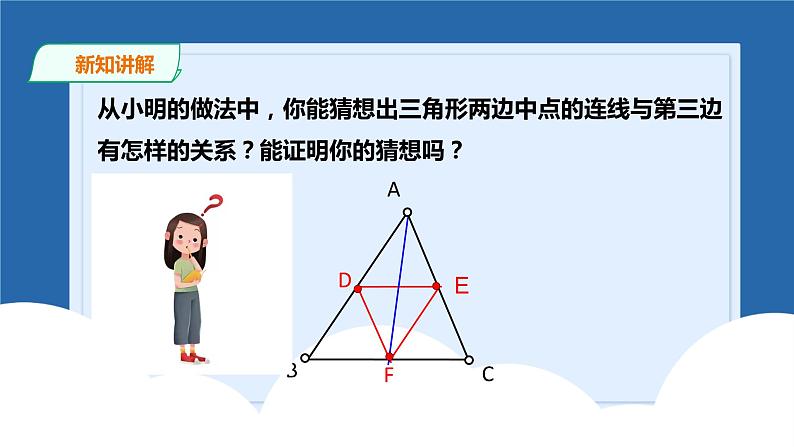
从小明的做法中，你能猜想出三角形两边中点的连线与第三边有怎样的关系？能证明你的猜想吗？
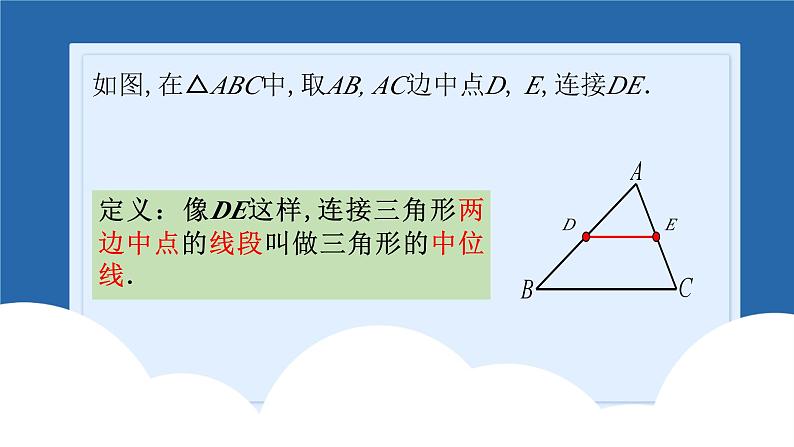
如图,在△ABC中,取AB, AC边中点D, E,连接DE．
定义：像DE这样,连接三角形两边中点的线段叫做三角形的中位线．
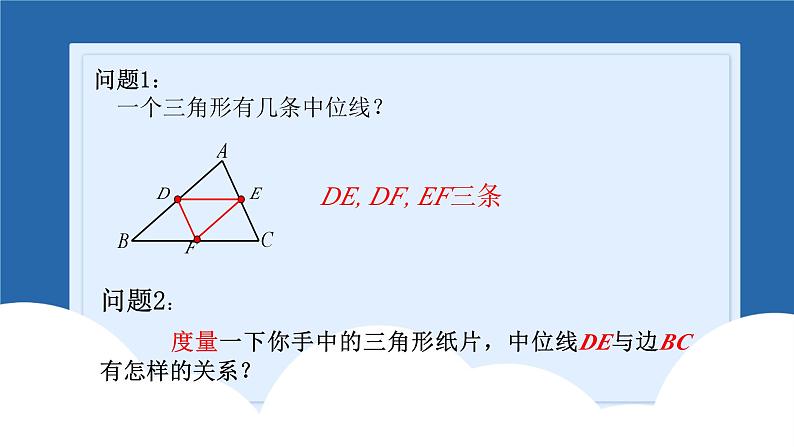
问题1： 一个三角形有几条中位线？
DE, DF, EF三条
度量一下你手中的三角形纸片，中位线DE与边BC有怎样的关系？
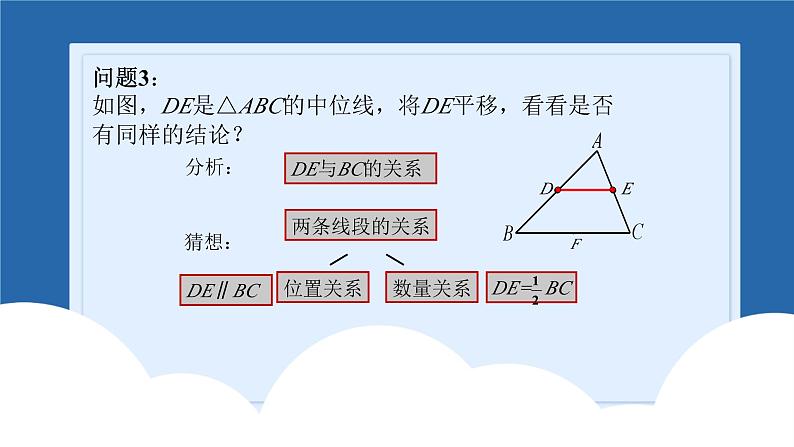
问题3：如图，DE是△ABC的中位线，将DE平移，看看是否有同样的结论？
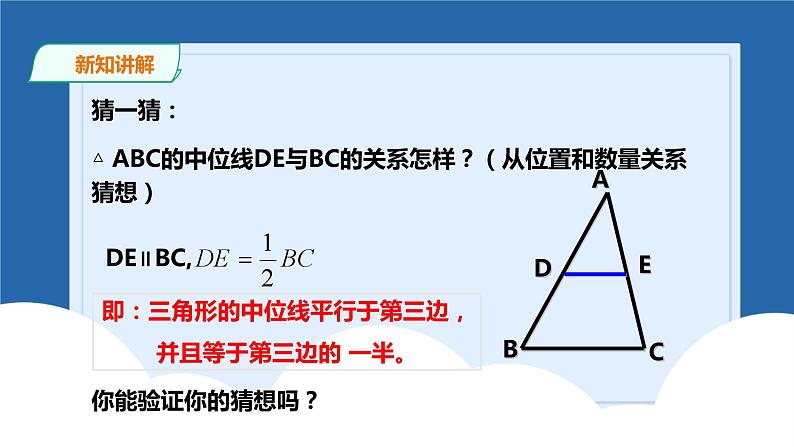
△ ABC的中位线DE与BC的关系怎样？（从位置和数量关系猜想）
即：三角形的中位线平行于第三边，并且等于第三边的 一半。
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE,∠AED=∠CEF,
∴△ABC≌△CDA(SAS).
∴AD=CF,∠ADE=∠F.
∴四边形ABCD是平行四边形.
∴DF∥BC,DF=BC.
(一组对边平等且相等的四边形是平行四边形)
如图，在△ABC中，D, E分别是AB, AC的中点.
若∠ADE=65°，则∠B= ；若BC=8cm， 则DE= cm.
② 若AC=4cm,BC=6cm，AB=8cm，则△DEF 的周长=______
1、 三角形三条中位线围成的三角形的周长是原三角形的周长的 .
2、三角形三条中位线围成的三角形的面积是原三角形的面积的 .
③图中有_____个平行四边形.
④若△ABC的面积为24，△DEF的面积是____.
如图,任意画一个四边形，顺次连结四边形四条边的中点，所得的四边形有什么特点？请证明你的结论，并与同伴交流。
解：四边形EFGH是平行四边形. 连接AC，在△ABC中， 因为E、F分别是AB、BC边的中点，即EF是△ABC的中位线. 所以EF//AC，EF= AC 在△ADC中，同理可得 HG//AC，HG= AC 所以EF//HG，EF=HG 所以四边形EFGH是平行四边形
（1）顺次连结对角线相等的四边形各边中点所得的四边形 是什么？ （2）顺次连结对角线垂直的四边形各边中点所得的四边形是什么？ （3）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么？
顺次连结对角线相等的四边形各边中点所得的四边形是菱形
（2）顺次连结对角线垂直的四边形各边中点所得的四边形是矩形
（3）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是正方形
变式1：如图, MN 为△ABC 的中位线,若∠ABC =59°则∠AMN = , 若MN =13 ,则BC =_______.
变式2：如图,已知△ABC中,AB = 4㎝,BC=4.6 ㎝ AC=6㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长是 ㎝.
变式3：如下图：在Rt △ ABC中，∠A=90°,D、E、F分别是各边中点, AB=9cm，AC=12cm，则△DEF的周长=______cm。
变式4：如图：工人师傅要把一块三角形的钢板，通过切割焊接成一个与其面积相等的平行四边形．请你设计一种方案并在图中标出焊接线，然后证明你的结论．　　　　　　　　　　　　　
沿中位线将三角形分割开，将得到的小三角形绕AC的中点旋转180度再与梯形拼接即可，如图所示：