
- 专题8.1 基本立体图形-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册) 试卷 1 次下载
- 专题8.2 立体图形的直观图-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册) 试卷 1 次下载
- 专题8.4 空间点、直线、平面之间的位置关系-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册) 试卷 0 次下载
- 专题8.5 空间直线、平面的平行-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册) 试卷 0 次下载
- 专题8.6 空间直线、平面的垂直(一)-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册) 试卷 0 次下载
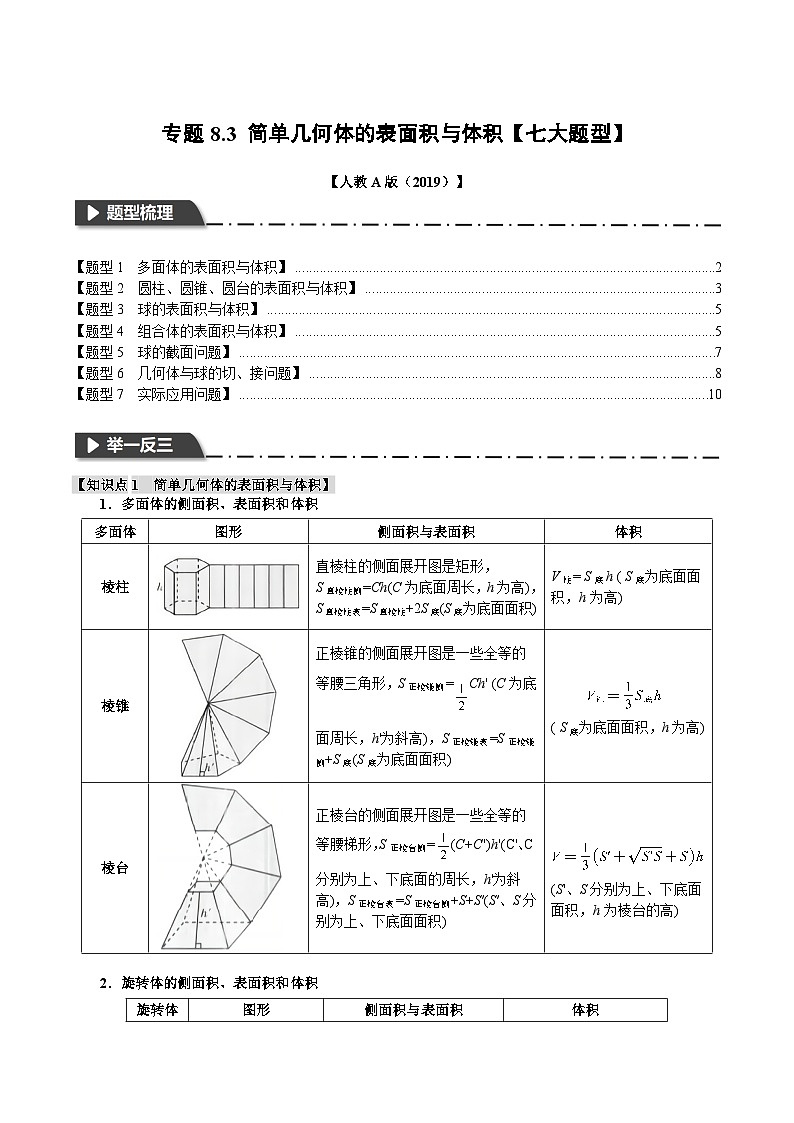
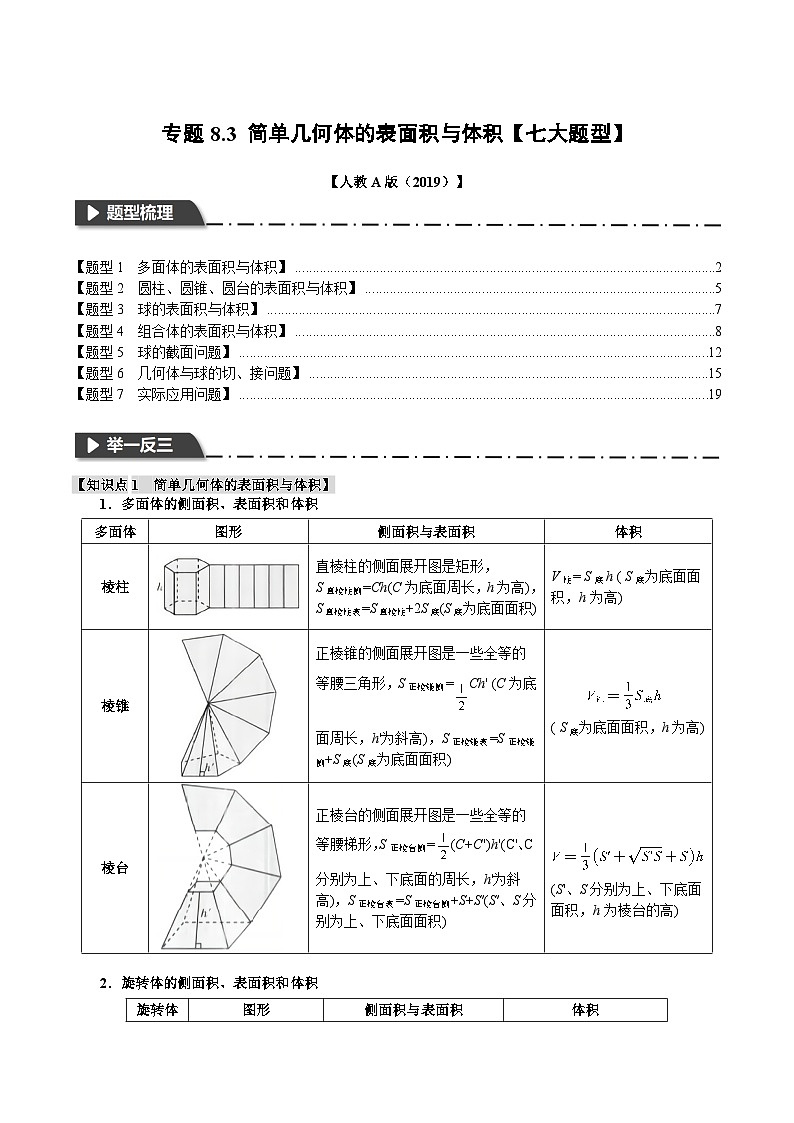
专题8.3 简单几何体的表面积与体积-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册)
展开TOC \ "1-3" \h \u
\l "_Tc28374" 【题型1 多面体的表面积与体积】 PAGEREF _Tc28374 \h 2
\l "_Tc5237" 【题型2 圆柱、圆锥、圆台的表面积与体积】 PAGEREF _Tc5237 \h 5
\l "_Tc24495" 【题型3 球的表面积与体积】 PAGEREF _Tc24495 \h 7
\l "_Tc28717" 【题型4 组合体的表面积与体积】 PAGEREF _Tc28717 \h 8
\l "_Tc13537" 【题型5 球的截面问题】 PAGEREF _Tc13537 \h 12
\l "_Tc24107" 【题型6 几何体与球的切、接问题】 PAGEREF _Tc24107 \h 15
\l "_Tc11848" 【题型7 实际应用问题】 PAGEREF _Tc11848 \h 19
【知识点1 简单几何体的表面积与体积】
1.多面体的侧面积、表面积和体积
2.旋转体的侧面积、表面积和体积
3.空间几何体表面积与体积的常见求法
(1)常见的求几何体体积的方法
①公式法:直接代入公式求解.
②等体积法:四面体的任何一个面都可以作为底面,只需选用底面面积和高都易求出的形式即可.
③补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,三棱柱补成四棱柱等.
④分割法:将几何体分割成易求解的几部分,分别求体积.
(2)求组合体的表面积与体积的方法
求组合体的表面积的问题,首先应弄清它的组成部分,其表面有哪些底面和侧面,各个面的面积应该
怎样求,然后根据公式求出各个面的面积,最后相加或相减.求体积时也要先弄清各组成部分,求出各简单几何体的体积,再相加或相减.
【题型1 多面体的表面积与体积】
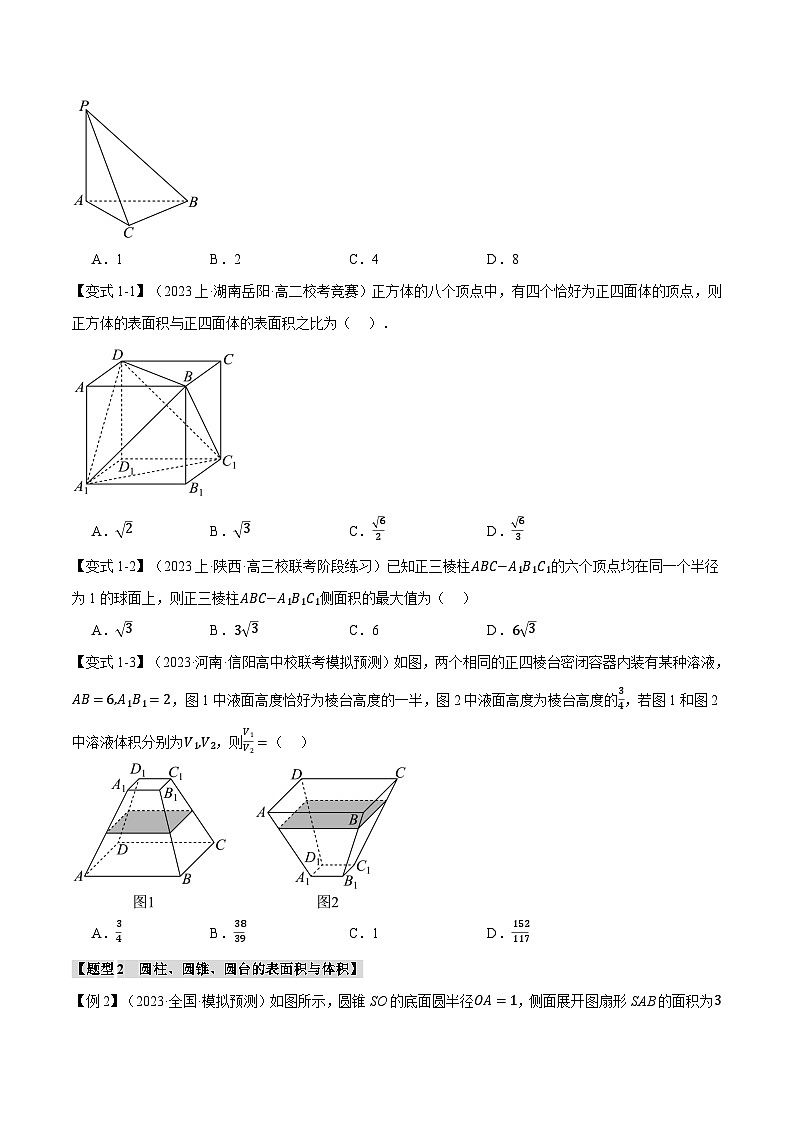
【例1】(2023上·黑龙江·高二统考学业考试)《九章算术》中记载,四个面都为直角三角形的四面体称之为鳖臑.现有一个“鳖臑”,PA⊥底面ABC,AC⊥BC,且PA=3,AC=BC=2,则该四面体的体积为( )
A.1B.2C.4D.8
【解题思路】根据锥体的体积公式运算求解.
【解答过程】由题意可知:三棱锥P−ABC的高为PA=3,
所以该四面体的体积为13×3×12×2×2=2.
故选:B.
【变式1-1】(2023上·湖南岳阳·高二校考竞赛)正方体的八个顶点中,有四个恰好为正四面体的顶点,则正方体的表面积与正四面体的表面积之比为( ).
A.2B.3C.62D.63
【解题思路】设正方体的棱长为a,可求出正四面体的棱长,继而求得两种几何体的表面积即可.
【解答过程】正方体的棱长为a,此时正四面体的棱长为2a,
则正方体的表面积为6a2,
正四面体的表面积为4×12×(2a)2sinπ3=23a2,
两者之比为6a223a2=3,
故选:B.
【变式1-2】(2023上·陕西·高三校联考阶段练习)已知正三棱柱ABC−A1B1C1的六个顶点均在同一个半径为1的球面上,则正三棱柱ABC−A1B1C1侧面积的最大值为( )
A.3B.33C.6D.63
【解题思路】利用正三棱柱外接球的性质得到a,ℎ的关系式,从而利用二次函数的性质或基本不等式即可得解.
【解答过程】解法一:
设正三棱柱底面边长为a,高为h,底面外接圆的半径为r,
则2r=asin60°=2a3,故r=a3,所以a32+ℎ22=1,即a23=1−ℎ24,
又三棱柱的侧面积S=3aℎ,
所以S2=9a2ℎ2=271−ℎ24ℎ2=274−ℎ4+4ℎ2=−274ℎ2−22+27≤27,
当ℎ=2时,等号成立,则三棱柱的侧面积S=3aℎ最大值为33.
解法二:
设正三棱柱底面边长为a,高为h,底面外接圆的半径为r,
则2r=asin60°=2a3,故r=a3,所以a32+ℎ22=1,
因为a23+ℎ24=1≥2a23⋅ℎ24=aℎ3,所以aℎ≤3,
当且仅当a=62,ℎ=2时,等号成立,则三棱柱的侧面积S=3aℎ最大值为33.
故选:B.
【变式1-3】(2023·河南·信阳高中校联考模拟预测)如图,两个相同的正四棱台密闭容器内装有某种溶液,AB=6,A1B1=2,图1中液面高度恰好为棱台高度的一半,图2中液面高度为棱台高度的34,若图1和图2中溶液体积分别为V1,V2,则V1V2=( )
A.34B.3839C.1D.152117
【解题思路】根据棱台的体积公式,求出V1,V2,即可解出.
【解答过程】设四棱台的高度为ℎ,在图1中,中间液面四边形的边长为4,在图2中,中间液面四边形的边长为5,
则V1=1336+16+36×16⋅ℎ2=38ℎ3,V2=134+25+4×25⋅3ℎ4=39ℎ4,
所以V1V2=152117.
故选:D.
【题型2 圆柱、圆锥、圆台的表面积与体积】
【例2】(2023·全国·模拟预测)如图所示,圆锥SO的底面圆半径OA=1,侧面展开图扇形SAB的面积为3π,则此圆锥的体积为( )
A.22π3B.4πC.πD.22π
【解题思路】根据圆锥侧面积公式求出母线长,再求出其高,最后利用体积公式即可.
【解答过程】设圆锥的母线长为l,则圆锥的侧面积S=12×2π×1×l=3π,所以l=3,
所以圆锥的高SO=32−1=22,
故圆锥的体积V=13×π×12×22=223π.
故选:A.
【变式2-1】(2023上·山东·高三校考期中)如图,圆锥的母线长为2,点M为母线AB的中点,从点M处拉一条绳子绕圆锥的侧面转一周到达B点,这条绳子的长度最短值为5,则此圆锥的表面积为( )
A.πB.54πC.32πD.2π
【解题思路】作出圆锥侧面展开图,根据给定条件求出展开图扇形圆心角,再求出圆锥底面圆半径即可作答.
【解答过程】将圆锥侧面沿母线AB剪开,其侧面展开图为扇形,如图,
从点M处拉一条绳子,绕圆锥的侧面转一周达到B点,最短距离即为线段BM长,则有BM=5,
而M是线段AB'中点,又母线长为2,于是得AM2+AB2=5=BM2,即∠BAB'=π2,
设圆锥底面圆半径为r,从而有:2πr=2⋅π2,解得r=12,
所以圆锥的表面积为S=πr2+πr⋅AB=5π4.
故选:B.
【变式2-2】(2023·浙江温州·高二统考学业考试)已知一个圆台的上底面半径为2,下底面的半径为5,其侧面积为35π,则该圆台的体积为( )
A.208πB.156πC.104πD.52π
【解题思路】根据圆台的侧面积公式求出母线,再求圆台的高结合圆台体积公式求体积即可.
【解答过程】设圆台上下底面的半径分别为r′,r,母线为l,
由题意可得:S侧=πr′+rl=35π⇒l=5,
则圆台的高为ℎ=l2−r−r′2=4,
所以圆台的体积为V=13πℎr2+rr′+r′2=52π.
故选:D.
【变式2-3】(2023上·辽宁·高三校联考期中)如图,在圆锥PO中,用一个平行于底面的平面去截圆锥PO,可得一个圆锥PO1和一个圆台O1O,若圆锥PO1的体积是圆锥PO体积的18,则圆锥PO1与圆台O1O的侧面积的比值为( )
A.12B.14C.23D.13
【解题思路】根据体积之比可得半径之比,即可根据圆锥和圆台的侧面积的公式即可求解.
【解答过程】设圆锥PO1,PO的底面圆半径分别为r,R,它们的母线长分别为l,L.
因为VPO1VPO=rR3=18,所以rR=12.从而lL=12,
即R=2r,L=2l.所以SPO1侧SOO1侧=πrlπ×2r⋅2l−πrl=13·
故选:D.
【题型3 球的表面积与体积】
【例3】(2023下·陕西西安·高一期中)两个球表面积的比为1:4,则体积的比为( )
A.1:2B.1:4
C.1:8D.不确定
【解题思路】由表面积的比得到半径之比,再得到体积之比.
【解答过程】设两球的半径分别为r1,r2,
∵表面积之比S1S2=4πr124πr22=14,∴ r1r2=12,
∴体积之比V1V2=43πr1343πr23=18.
故选:C.
【变式3-1】(2023上·上海·高二专题练习)若两球的体积之和是12π,经过两球球心的截面圆周长之和为 6π,则两球的半径之差为( )
A.1B.2C.3D.4
【解题思路】设两球的半径分别为R,r(R>r),根据题意得到方程,解出即可.
【解答过程】设两球的半径分别为R,r(R>r),则由题意得4π3R3+4π3r3=12π2πR+2πr=6π,
解得R=2r=1,故R−r=1;
故选:A.
【变式3-2】(2023·陕西商洛·统考一模)将一个底面半径为3,高为4的圆柱形铁块熔化为铁水,恰好制成一个实心铁球,则该实心铁球的半径是( )
A.2B.3C.4D.6
【解题思路】根据题意,求得圆柱的体积,结合球的体积公式,列出方程,即可求解.
【解答过程】由题意,可得圆柱的体积为V=πr2ℎ=π×32×4=36π,
设该实心铁球的半径为R,则43πR3=36π,解得R=3.
故选:B.
【变式3-3】(2023上·四川南充·高二校考阶段练习)如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的表面积与球的表面积之比为( )
A.65B.54C.32D.76
【解题思路】根据圆柱的表面积公式和球的表面积公式求解.
【解答过程】设球半径为r,则圆柱底面半径为r,高为2r,
所以圆柱的表面积S1与球的表面积S2之比为S1S2=2πr2+2πr⋅2r4π2=32,
故选:C.
【题型4 组合体的表面积与体积】
【例4】(2023上·山东滨州·高三校联考阶段练习)我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,是过去官员或私人签署文件时代表身份的信物。图1是明清时期的一个金属印章摆件,除去顶部的环以后可以看作是一个正四棱柱和一个正四棱锥组成的几何体,如图2.已知正四棱柱和正四棱锥的高相等,且正四棱锥的底面边长为4,侧棱长为23,则该几何体的体积是( )
A.32B.643C.1283D.64
【解题思路】根据正四棱锥的几何性质,建立方程,求得其高,结合体积公式,可得答案.
【解答过程】解:因为正四棱锥的底面边长为4,所以底面的对角线长为42,
设正四棱柱和正四棱锥的高为ℎ,
因为正四棱锥的侧棱长为23,所以ℎ2+222=232,解得ℎ=2,
故该几何体的体积为4×4×2+13×4×4×2=1283.
故选:C.
【变式4-1】(2023上·河南周口·高三校联考阶段练习)中国是瓷器的故乡,“瓷器”一词最早见之于许慎的《说文解字》中.某瓷器如图1所示,该瓷器可以近似看作由上半部分圆柱和下半部分两个圆台组合而成,其直观图如图2所示,已知圆柱的高为18cm,底面直径AB=12cm,CD=20cm,EF=14cm,中间圆台的高为3cm,下面圆台的高为4cm,若忽略该瓷器的厚度,则该瓷器的侧面积约为( )
A.375πcm2B.377πcm2C.379πcm2D.381πcm2
【解题思路】先计算两个圆台的母线长,根据圆柱和圆台的侧面积公式和可得该瓷器的侧面积.
【解答过程】由AC=32+CD−AB22=32+20−1222=5cm,CE=42+CD−EF22=42+20−1422=5cm,
可得该瓷器的侧面积为12π×18+5×(6+10)π+5×(7+10)π=381πcm2.
故选:D.
【变式4-2】(2023·陕西安康·校联考模拟预测)陀螺是中国民间最早的娱乐工具之一,如图所示,某陀螺可以视为由圆锥SO和圆柱OO1组合而成,点M,N在圆锥SO的底面圆周上,且△SMN的面积为7,sin∠MSN=74,圆锥SO的侧面积为42π,圆柱OO1的母线长为3,则该几何体的体积为( )
A.40π3B.44π3C.52π3D.56π3
【解题思路】该几何体是由一个圆锥和一个圆柱组成的,由S△SMN=7,sin∠MSN=74可得圆锥母线,结合圆锥的侧面积可得圆锥半径、高,而圆柱底面半径等于圆锥底面半径,圆柱高已知,由圆锥、圆柱体积公式即可得解.
【解答过程】设圆锥的底面半径为r,母线长为l,则△SMN的面积为12SM×SNsin∠MSN=12l×l×74=7,解得l=22,
因为圆锥SO的侧面积为πrl=22πr=42π,所以r=2,SO=l2−r2=2.
故该几何体的体积为V=V圆柱+V圆锥=4π×3+13×4π×2=44π3.
故选:B.
【变式4-3】(2023上·湖北·高二荆州中学校考阶段练习)贯耳瓶流行于宋代,清代亦有仿制,如图所示的青花折枝花卉纹六方贯耳瓶是清乾隆时期的文物,现收藏于首都博物馆,若忽略瓶嘴与贯耳,把该瓶瓶体看作3个几何体的组合体,上面的几何体Ⅰ是直棱柱,中间的几何体Ⅱ是棱台,下面的几何体Ⅲ也是棱台,几何体Ⅲ的下底面与几何体Ⅰ的底面是全等的六边形,几何体Ⅲ的上底面面积是下底面面积的9倍,若几何体Ⅰ、Ⅱ、Ⅲ的高之比分别为3:3:5,则几何体Ⅰ、Ⅱ、Ⅲ的体积之比为( )
A.3:9:25B.9:21:35C.3:39:65D.9:39:65
【解题思路】设上面的六棱柱的底面面积为S,高为3m,根据棱柱和棱台的体积公式直接计算,然后求比可得.
【解答过程】设上面的六棱柱的底面面积为S,高为3m,由上到下的三个几何体体积分别记为V1,V2,V3,
则V1=3mS,
V2=13S+9S+9S2×3m=13mS,
V3=13S+9S+9S2×5m=653mS,
所以V1:V2:V3=3mS:13mS:653mS=9:39:65.
故选:D.
【知识点2 球的截面、几何体与球的切、接问题】
1.球的截面
(1)球的截面形状
①当截面过球心时,截面的半径即球的半径,此时球的截面就是球的大圆;
②当截面不过球心时,截面的半径小于球的半径,此时球的截面就是球的小圆.
(2)球的截面的性质
①球心和截面圆心的连线垂直于截面;
②球心到截面的距离d与球的半径R及截面的半径r之间满足关系式:.
图形解释如下:
在球的轴截面图中,截面与球的轴截面的关系如图所示.若设球的半径为R,以O'为圆心的截面的半径
为r,OO'=d.则在Rt△OO'C中,有,即.
2.几何体与球的切、接问题
常见的与球有关的组合体问题有两种:一种是内切球,另一种是外接球.
常见的几何体与球的切、接问题的解决方案:
【题型5 球的截面问题】
【例5】(2023·全国·高三专题练习)某同学在参加《通用技术》实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为43的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),若其中一个截面圆的周长为4π,则该球的体积是( )
A.256π3B.64πC.16πD.32π3
【解题思路】求出球心到截面圆所在平面的距离以及截面圆的半径,利用勾股定理可求得球的半径,再利用球的体积公式即可求得结果.
【解答过程】由题意可得,球心到截面圆所在的平面的距离d=432=23,
设截面圆的半径为r,球的半径为R,则2πr=4π,解得r=2,
所以R=r2+d2=4,
所以该球的体积为43πR3=256π3,
故选:A.
【变式5-1】(2023上·湖北荆州·高三沙市中学校考阶段练习)三棱锥A−BCD的四个顶点都在表面积为20π的球O上,点A在平面BCD的射影是线段BC的中点,AB=BC=23,则平面BCD被球O截得的截面面积为( )
A.23πB.3π
C.4πD.33π
【解题思路】分别找出△BCD和△ABC的外接圆圆心F和H,通过过F作平面BCD的垂线,过H作平面ABC的垂线,两垂线的交点即为三棱锥A−BCD外接球球心O,再通过几何关系求出△BCD外接圆半径,即可求其被球O截得的圆的面积.
【解答过程】
设BC中点为E,∵点A在平面BCD的射影是线段BC的中点E,
∴AE⊥平面BCD,AE⊥BC,∴AB=AC,
又∵AB=BC,∴△ABC是等边三角形.
取AC中点为G,连接BG交AE于H,则H是△ABC外心.
连接ED,在ED上取F,使得FD=2EF,则F为△BCD外心.
过F作平面BCD的垂线,过H作平面ABC的垂线,
两垂线的交点即为三棱锥A−BCD外接球球心O,
则四边形OHEF是矩形,OF=HE=13AE=13×32×23=1.
连接OB,BF,设△BCD外接圆半径FD=BF=r,设球O半径为OB=R.
∵球O的表面积为20π,∴4πR2=20π⇒R=5.
∴在Rt△OBF中,r=BF=R2−OF2=5−1=2,
∴平面BCD被球O截得的截面面积πr2=4π.
故选:C.
【变式5-2】(2023·全国·高三专题练习)已知三棱锥P−ABC满足PA⊥底面ABC,在△ABC中,AB=6,AC=8,AB⊥AC,D是线段AC上一点,且AD=3DC,球O为三棱锥P−ABC的外接球,过点D作球O的截面,若所得截面圆的面积的最小值与最大值之和为44π,则球O的表面积为( )
A.72πB.86πC.112πD.128π
【解题思路】先找到外接球球心,过BC的中点M作OM//PA,则OM⊥平面ABC,取OM=12PA,则O为P−ABC外接球球心,过点D作球O的截面,最大的截面过球心,最小的截面是过D且与OD垂直的截面,由此可用PA表示出两截面圆半径.
【解答过程】如图,M是BC边中点,E是AC边中点,∵AB⊥AC,∴M是△ABC的外心,
作OM//PA,∵PA⊥平面ABC,∴OM⊥平面ABC,AM,MD⊂平面ABC,
∴OM⊥AM,OM⊥MD,取OM=12PA,易得OA=OP,
∴O是三棱锥P−ABC的外接球的球心.
E是AC中点,则ME//AB,ME=12AB=3,∴ME⊥AC,
∵AD=3DC,∴ED=14AC=2,∴MD=ME2+ED2=32+22=13,
设PA=2a,则OM=a,OD2=OM2+MD2=a2+13,又AM=12BC=1262+82=5,
∴OA2=OM2+AM2=a2+25,
过D且与OD垂直的截面圆半径为r,则r=OA2−OD2=23,
这是最小的截面圆半径,最大的截面圆半径等于球半径OA,
∴πOA2+πr2=(a2+25)π+12π=44π,a2=7,
OA2=a2+25=7+25=32,S球=4πOA2=4π×32=128π.
故选:D.
【变式5-3】(2023下·浙江·高二校联考阶段练习)在三棱锥A−BCD中,AB,BC,BD两两垂直,且AB=BC=BD=4,半径为1的球O在该三棱锥内部且与面ABC、面ABD、面BCD均相切.若平面α与球O相切,则三棱锥A−BCD的外接球被平面α所截得的截面面积的最小值为( )
A.8+23πB.6+23πC.8−23πD.6−23π
【解题思路】先推出球的截面面积与球心距离的关系,再根据条件将三棱锥A−BCD看作正方体的一部分,求出外接球的球心和半径,运用前面推出的关系求解.
【解答过程】设截面圆与球心O1的距离为h,球O1的半径为R,截面圆的半径为r,则r2=R2−ℎ2,
即h越大,截面的面积越小;
由题意三棱锥A−BCD是正方体AEGF−BCHD的一部分,
其外接球的球心为正方体对角线AH的中点O1,
外接球的半径R,则R=42+42+422=23,如下图:
以BC为x轴,BD为y轴,BA为z轴建立坐标系,则O1,1,1,O12,2,2,∴OO1=2−12+2−12+2−12=3,
O1到球O球面上最远的点距离为ℎ=OO1+1=3+1,
此时以最远点为切点的平面α截外接球O1截面圆的半径为r=232−3+12=8−23,
即截面面积的最小值为S=r2π=8−23π;
故选:C.
【题型6 几何体与球的切、接问题】
【例6】(2023上·上海闵行·高二校考期末)我国古代数学名著《九章算术》,将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.如图所示,在长方体ABCD−A1B1C1D1中,已知AB=BC=2,AA1=3.
(1)求证:四棱锥D1−ABCD是一个“阳马”,并求该“阳马”的体积;
(2)求该“阳马”D1−ABCD的外接球的表面积.
【解题思路】(1)根据DD1⊥平面ABCD,且ABCD是矩形,可证明四棱锥是“阳马”,根据锥体的体积公式可求其体积;
(2)根据长方体的外接球即为四棱锥的外接球,长方体的对角线就是外接球的直径,结合球体的表面积公式求解.
【解答过程】(1)因为长方体ABCD−A1B1C1D1中,DD1⊥平面ABCD,且ABCD是矩形,
所以四棱锥D1−ABCD中,底面ABCD是矩形,且侧棱DD1⊥底面ABCD,
所以四棱锥D1−ABCD是一个“阳马”,
体积V=13SABCD×DD1=13×2×2×3=4;
(2)长方体的外接球即为四棱锥的外接球,
因为AB=BC=2,AA1=3.
∴长方体的对角线长为22+22+32=17,
则长方体的外接球的半径R=172,
∴该“阳马”外接球的表面积为S=4πR2=4π×(172)2=17π.
【变式6-1】(2023·全国·高三专题练习)如图所示,在棱长为1的正方体内有两个球相外切且分别与正方体内切,求两球半径之和.
【解题思路】作正方体的对角面,设出两球半径,根据正方体的对角线长列出等式,即可求得答案.
【解答过程】作正方体的对角面,得如图所示的截面图:其中AB,CD为正方体的棱,AD,BC为正方体的面对角线,AC为体对角线,
球心O1和O2在AC上,过O1,O2分别作AD,BC的垂线交于E,F两点.
设小球半径为r,大球半径为R,则由题意知AB=1,∴AC=3,
得AO1=r2+r2+r2=3r,CO2=R2+R2+R2=3R,
∴r+R+3(r+R)=3,
∴R+r=33+1=3−32,即两球半径之和为3−32.
【变式6-2】(2023上·江西景德镇·高二校考期中)已知圆锥的顶点为P,母线PA,PB所成角的余弦值为14,轴截面等腰三角形的顶角为90°,若△PAB的面积为215.
(1)求该圆锥的侧面积;
(2)求圆锥的内切球体积.
【解题思路】(1)先由已知得出l=2r,sin∠APB=154,再由三角形面积公式得出l,从而得出r以及圆锥的侧面积.
(2)画出截面图形,先由相似三角形知识求出内切球半径,再由体积公式即可求解.
【解答过程】(1)如图所示:
令圆锥母线长、底面半径分别为l、r,
由圆锥的轴截面为等腰三角形且顶角为90°知,l=2r,
又cs∠APB=14⇒sin∠APB=1−cs2∠APB=1−142=154,
又因为△PAB的面积为215,
∴S△PAB=12PA⋅PB⋅sin∠APB=12l2×154=215⇒l=4,
又l=2r,所以r=22,
∴侧面积为S=12×2πr×l=π×22×4=82π.
(2)如图所示:
设内切球半径为CO=CD=R,球心C在PO上面,则△POA∼△PDC,
所以CDAO=PCPA,
由(1)可知,圆锥的高PO=AO=ℎ=r=22l=22,PA=l=4,
则有R22=22−R4,解得R=4−22,
所以圆锥的内切球体积为V=43πR3=43π4−223=6410−72π3.
【变式6-3】(2023下·辽宁·高一校联考阶段练习)《九章算术.商功》中,将四个面都是直角三角形的四面体称为鳖臑;在鳖臑ABCD中,AB⊥平面BCD,BC⊥CD,且AB=BC=CD=1,求
(1)四面体ABCD的表面积;
(2)四面体ABCD内切球半径;
(3)四面体ABCD外接球的表面积.
【解题思路】(1)根据四个面均为直角三角形,求出各个面的面积再相加即可;
(2)根据等体积法即可求解;
(3)根据直角三角形的性质找出外接球球心,再得到外接球半径,根据球的表面积公式计算即可得到答案.
【解答过程】(1)因为AB⊥面BCD,BC,BD,CD⊂面BCD,
所以AB⊥BC,AB⊥BD,AB⊥CD,
又因为BC⊥CD,AB,BC⊂面ABC,AB∩BC=B,所以CD⊥面ABC,
因为AC⊂面ABC,所以CD⊥AC.
所以∠ABC=∠ABD=∠ACD=∠BCD=90°.
由题意得,AB=BC=CD=1
则S△ABC=12AB⋅BC=12,同理S△BCD=12,
因为在Rt△ABC中,AC=AB2+BC2=2,
所以S△ACD=12AC⋅CD=22,同理S△ABD=22,
所以四面体ABCD的表面积S=S△ABC+S△ABD+S△ACD+S△BCD=1+2;
(2)设内切球球心为O,半径为r,
显然VA−BCD=13AB⋅S△BCD=13×1×12=16,
由体积相等得
VA−BCD=VO−ABC+VO−ABD+VO−ACD+VO−BCD=13rS△ABC+S△ABD+S△ACD+S△BCD,
得到r=3VA−BCDS=122+12−12;
(3)由题意得,∠ABD=∠ACD=90∘,
所以取AD中点为P,
则PA=PB=PC=PD
所以P为四面体外接球的球心,AD为直径,
在Rt△ABD中,AD=AB2+BD2=3,
所以四面体外接球的半径为r=AD2=32,
所以四面体外接球面积为S=4πr2=4πr2×34=3π.
【题型7 实际应用问题】
【例7】(2023上·上海·高二期中)某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
(1)求这种“笼具”的体积(结果精确到0.1cm3);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
【解题思路】(1)根据题意,结合圆锥和圆柱的体积公式,即可求解;
(2)根据题意,求得该组合体的表面积,结合题意,即可求解.
【解答过程】(1)设圆柱的底面半径为r,高为ℎ,圆锥的母线长为l,高为ℎ1,
则2πr=24π,可得r=12,且ℎ1=202−122=16cm,
所以笼具的体积V=πr2ℎ−13πr2ℎ1=π⋅(122×30−13×122×16)=3552π≈11158.9cm2.
(2)圆柱的侧面积S1=2πrℎ=720πcm2,
圆柱的底面积S2=πr2=144πcm2,
圆锥的侧面积为S3=πrl=240πcm2,
故笼具的表面积S=S1+S2+S3=1104πcm2.
故制造50个这样的笼具总造价为:1104π×50×8104=1104π25元,
答:这种笼具的体积约为11158.9cm2,生产50个笼具需要1104π25元.
【变式7-1】(2023·全国·高一随堂练习)用铁皮裁剪成两个圆和一个长方形,焊成一个体积固定的圆柱体容器
(1)为使用料最省,应如何设计这个圆柱体?
(2)为使接缝线最短,应如何设计这个圆柱体?
【解题思路】由体积固定,将圆柱表面积和接缝总长用体积和底面半径表示,求出取最值的条件.
【解答过程】(1)设圆柱体积为V,底面半径r,高为h,则V=πr2ℎ,
圆柱用料,即表面积为S=2πr2+2πrℎ=2πr2+2Vr=2(πr2+V2r+V2r)≥332πV2,
当且仅当πr2=V2r,即πr2ℎ=2πr3,ℎ=2r时,等号成立,
所以设计时,使圆柱的轴截面为正方形,可使用料最省.
(2)设接缝总长度为C,
则C=4πr+ℎ=4πr+Vπr2=2πr+2πr+Vπr2≥334πV,
当且仅当2πr=Vπr2,即2πr=ℎ时,等号成立,
所以设计时,使圆柱的高等于底面周长,可使接缝最短.
【变式7-2】(2023下·山东青岛·高一校考期中)如图,某种水箱用的“浮球”是由两个半球和一个圆柱筒组成,已知半球的直径是6cm,圆柱筒长2cm.
(1)这种“浮球”的体积是多少cm3?
(2)要在100个这样的“浮球”表面涂一层胶质,如果每平方厘米需要涂胶20克,那么共需涂胶约多少克?
【解题思路】(1)利用球和圆柱体积公式即可求解得到结果;
(2)结合球的表面积和圆柱侧面积公式可求得几何体的表面积,
进而确定所需胶的质量.
【解答过程】(1)∵该半球的直径d=6cm,
∴“浮球”的圆柱筒直径也是6cm,R=3cm,
∴两个半球的体积之和为V球=43πR3=43π×27=36πcm3,
又V圆柱=πR2ℎ=π×9×2=18πcm3,
该“浮球”的体积是V=V球+V圆柱=36π+18π=54πcm3.
(2)上下两个半球的表面积S球表=4πR2=4π×9=36πcm2,
“浮球”的圆柱筒侧面积为S圆柱侧=2πRℎ=2π×3×2=12πcm2,
∴1个“浮球”的表面积为36π+12π=48πcm2,
∴100个“浮球”的表面积的和为100×48π=4800πcm2,
∵每平方厘米需要涂胶20克,
∴共需要胶的质量为20×4800πcm2=96000π(克).
【变式7-3】(2023上·上海普陀·高二校考期中)某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r+1(l为圆柱的高,为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为1千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.
(1) 写出y关于r的函数表达式,并求该函数的定义域;
(2) 若预算为8万元,求所能建造的储油罐中r的最大值(精确到0.1),并求此时储油罐的体积V(单位: 立方米,精确到0.1立方米).
【解题思路】(1)先利用公式计算两个半球的表面积(不含底)以及圆柱的侧面积,再根据每平方米建造费用可得y关于r的函数表达式,注意r的范围.
(2)根据预算可得关于r的不等式,求出其解后可得r的最大值,利用公式可求该几何体的体积.
【解答过程】(1) 半球的表面积S1=2πr2(不含底),圆柱的侧面积S2=2πr⋅l.
于是y=3×2S1+1×S2=3×4πr2+1×2πr⋅(2r+1)=16πr2+2πr.
定义域为12,+∞.
(2) 16πr2+2πr≤80,即r2+18r−5π≤0,解得r≤−18+164+20π2≈1.2.
V=43πr3+πr2⋅(2r+1)=103πr3+πr2,
经计算得V≈22.7(立方米).
故r的最大值为1.2(米),此时储油罐的体积约为22.7立方米.
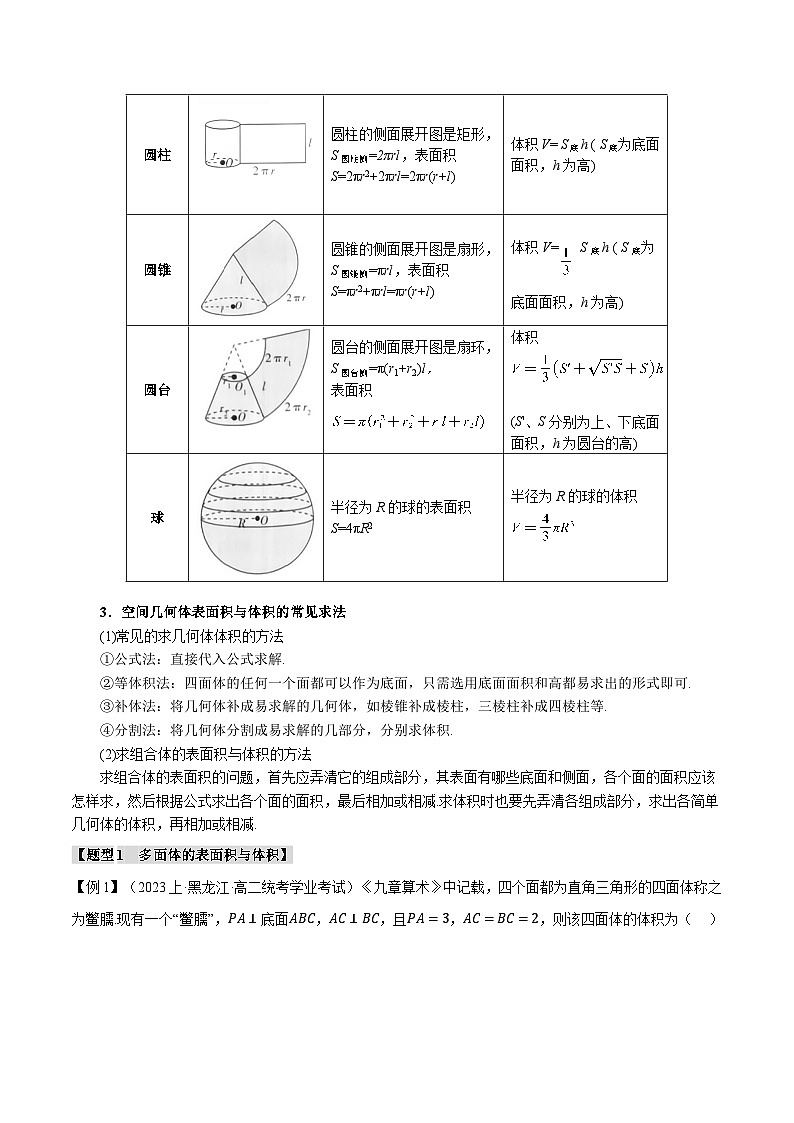
多面体
图形
侧面积与表面积
体积
棱柱
直棱柱的侧面展开图是矩形,
S直棱柱侧=Ch(C为底面周长,h为高),
S直棱柱表=S直棱柱+2S底(S底为底面面积)
V柱= S底h ( S底为底面面积,h为高)
棱锥
正棱锥的侧面展开图是一些全等的等腰三角形,S正棱锥侧=Ch' (C为底面周长,h'为斜高),S正棱锥表=S正棱锥侧+S底(S底为底面面积)
( S底为底面面积,h为高)
棱台
正棱台的侧面展开图是一些全等的等腰梯形,S正棱台侧=(C+C')h'(C'、C分别为上、下底面的周长,h'为斜高),S正棱台表=S正棱台侧+S+S′(S′、S分别为上、下底面面积)
(S'、S分别为上、下底面面积,h为棱台的高)
旋转体
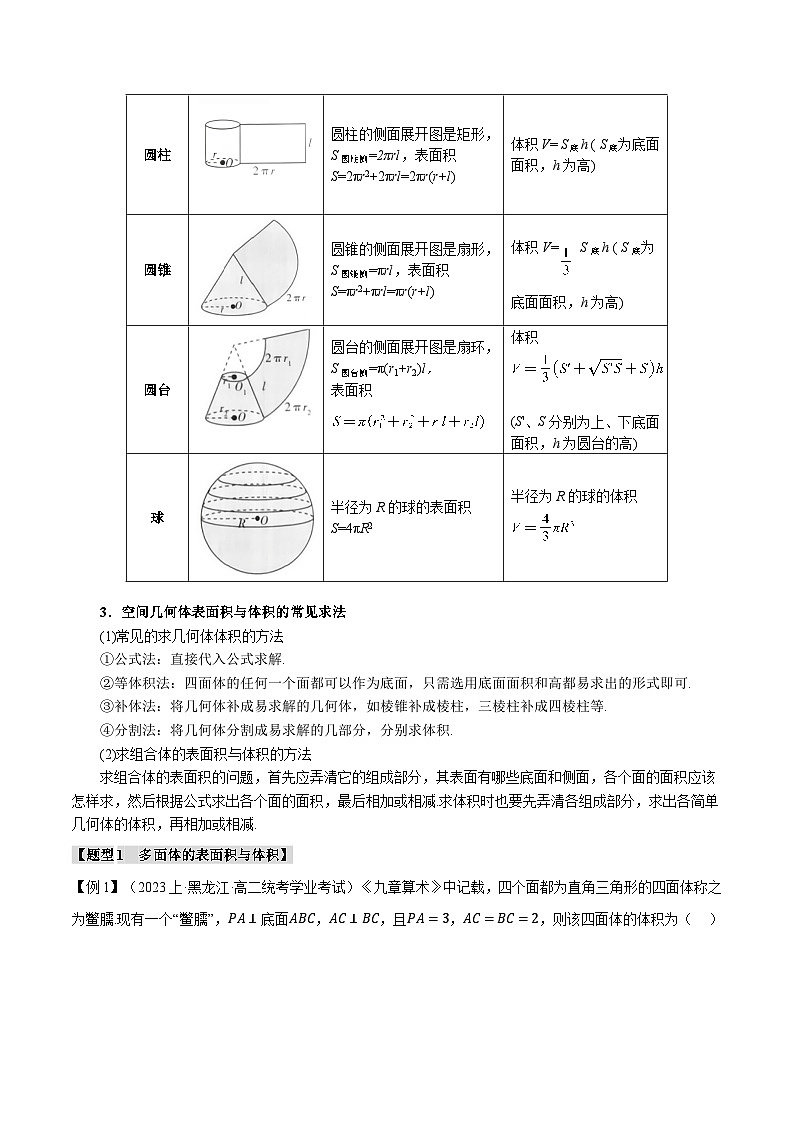
图形
侧面积与表面积
体积
圆柱
圆柱的侧面展开图是矩形,S圆柱侧=2πrl,表面积S=2πr2+2πrl=2πr(r+l)
体积V= S底h ( S底为底面面积,h为高)
圆锥
圆锥的侧面展开图是扇形,S圆锥侧=πrl,表面积
S=πr2+πrl=πr(r+l)
体积V= S底h ( S底为底面面积,h为高)
圆台
圆台的侧面展开图是扇环,S圆台侧=π(r1+r2)l,
表面积
体积
(S'、S分别为上、下底面面积,h为圆台的高)
球
半径为R的球的表面积S=4πR2
半径为R的球的体积
专题6.5 平面向量的应用-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册): 这是一份专题6.5 平面向量的应用-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册),文件包含专题65平面向量的应用举一反三人教A版必修第二册原卷版docx、专题65平面向量的应用举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
专题6.3 向量的数量积-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册): 这是一份专题6.3 向量的数量积-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册),文件包含专题63向量的数量积举一反三人教A版必修第二册原卷版docx、专题63向量的数量积举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
专题6.2 平面向量的运算-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册): 这是一份专题6.2 平面向量的运算-2023-2024学年高一数学下学期高效讲练测(人教A版必修第二册),文件包含专题62平面向量的运算举一反三人教A版必修第二册原卷版docx、专题62平面向量的运算举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。












