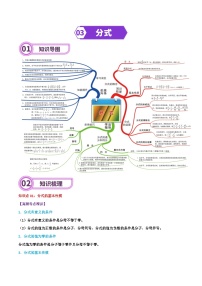
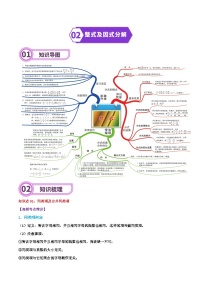
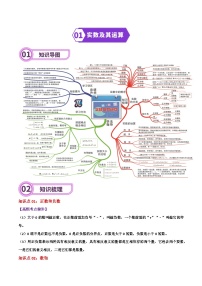
专题10 平面直角坐标系与函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测)
展开知识点01:坐标确定位置及点的坐标规律
【高频考点精讲】
1.各个象限内,点P(a,b)的坐标特征
(1)第一象限:a>0,b>0;(2)第二象限:a<0,b>0;
(3)第三象限:a<0,b<0;(4)第四象限:a>0,b<0。
2.坐标轴上,点P(a,b)的坐标特征
(1)x轴上:a为任意实数,b=0;(2)y轴上:b为任意实数,a=0;(3)坐标原点:a=0,b=0。
3.两坐标轴夹角平分线上,点P(a,b)的坐标特征
(1)一、三象限:a=b;(2)二、四象限:a=﹣b。
知识点02:坐标与图形性质
【高频考点精讲】
1.“点到坐标轴的距离”与“点的坐标”的区别
(1)到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关。
(2)“距离”是非负数,但是“坐标”可以是负数,由距离求坐标时,需要加上恰当的符号。
2.由图形中已知点的坐标求面积时,过已知点向坐标轴作垂线,求出相关线段的长度,是解决此类问题的基本方法和规律。
3.如果坐标系内的四边形是不规则四边形,可以借助平行于坐标轴的辅助线,将图形割补成边与坐标轴平行(或垂直)且顶点坐标已经的规则图形,通过规则图形面积的和差来计算不规则图形的面积。
检测时间:90分钟 试题满分:100分 难度系数:0.56
1.(2分)(2023•盐城)在平面直角坐标系中,点A(1,2)在( )
A.第一象限B.第二象限C.第三象限D.第四象限
解:∵点A(1,2)的横坐标和纵坐标均为正数,
∴点A(1,2)在第一象限.
故选:A.
2.(2分)(2023•内蒙古)若实数m,n是一元二次方程x2﹣2x﹣3=0的两个根,且m<n,则点(m,n)所在象限为( )
A.第一象限B.第二象限C.第三象限D.第四象限
解:由题意,∵m,n是一元二次方程x2﹣2x﹣3=0的两个根,
∴m+n=2>0,mn=﹣3<0.
∴m,n异号,且m,n中绝对值较大的为正.
又m<n,
∴m<0,n>0.
∴(m,n)在第二象限.
故选:B.
3.(2分)(2023•鄂州)如图,在平面直角坐标系中,O为原点,OA=OB=3,点C为平面内一动点,BC=,连接AC,点M是线段AC上的一点,且满足CM:MA=1:2.当线段OM取最大值时,点M的坐标是( )
A.(,)B.(,)
C.(,)D.(,)
解:∵点C为平面内一动点,BD=,
∴点C在以点B为圆心,为半径的OB上,
在x轴的负半轴上取点D(﹣,0),
连接BD,分别过C、M作CF⊥OA,ME⊥OA,垂足为F、E,
∵OA=OB=,
∴AD=OD+OA=,
∴=,
∵CM:MA=1:2,
∴==,
∵∠OAM=∠DAC,
∴△OAM∽△DAC,
∴==,
∴当CD取得最大值时,OM取得最大值,结合图形可知当D,B,C三点共线,且点B在线段DC上时,CD取得最大值,
∵OA=OB=,OD=,
∴BD==,
∴CD=BC+BD=9,
∵=,
∴OM=6,
∵y轴⊥x轴,CF⊥OA,
∴∠DOB=∠DFC=90°,
∵∠BDO=∠CDF,
∴△BDO∽△CDF,
∴=,即=,
解得CF=,
同理可得,△AEM∽△AFC,
∴==,即=,
解得ME=,
∴OE==,
∴当线段OM取最大值时,点M的坐标是(,),
故选D.
4.(2分)(2023•台州)如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位置的坐标为(﹣2,2),则“炮”所在位置的坐标为( )
A.(3,1)B.(1,3)C.(4,1)D.(3,2)
解:如图所示:“炮”所在位置的坐标为:(3,1).
故选:A.
5.(2分)(2023•金昌)如图1,正方形ABCD的边长为4,E为CD边的中点.动点P从点A出发沿AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,线段PE的长为y,y与x的函数图象如图2所示,则点M的坐标为( )
A.(4,2)B.(4,4)C.(4,2)D.(4,5)
解:由题意可知,当点P在边AB上时,y的值先减小后增大,
当点P在边BC上时,y的值逐渐减小,
∴M点的横坐标为AB的长度,纵坐标为BE的长度,
∵AB=4,EC=ED=AB=×4=2,
∴BE===2,
∴M(4,2),
故选:C.
6.(2分)(2023•齐齐哈尔)如图,在正方形ABCD中,AB=4,动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M
运动的路程为x(0≤x≤4),△DMN的面积为S,下列图象中能反映S与x之间函数关系的是( )
A.B.
C.D.
解:0≤x≤4时,M在AB上,N在BC上,依题意可知:
设AM=BN=x,
∴CN=4﹣x,
S=S正方形ABCD﹣S△AMD﹣S△BMN﹣S△DNC
=4×4﹣×4x﹣×(4﹣x)x﹣×4×(4﹣x)
=(x﹣2)2+6;
∴该二次函数图象开口向上,
当x=2时,二次函数的最小值为6;
当x=0或4时,二次函数的最大值为8;
故选:A.
7.(2分)(2023•绥化)如图,在菱形ABCD中,∠A=60°,AB=4,动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A﹣B﹣C向终点C运动;点N以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( )
A.B.
C.D.
解:连接BD,过B作BE⊥AD于E,当0≤x<2时,点M在AB上,
在菱形ABCD中,∠A=60°,AB=4,
∴AB=AD,
∴△ABD是等边三角形,
∴AE=ED=AD=2,BE=AE=2,
∵AM=2x,AN=x,
∴,
∵∠A=∠A,
∴△AMN∽△ABE,
∴∠ANM=∠AEB=90°,
∴=x,
∴y=x×x=x2,
当2≤x≤4时,点M在BC上,
y=,
综上所述,当 0≤x<2时的函数图象是开口向上的抛物线的一部分,当2≤x≤4时,函数图象是直线的一部分,
故选:A.
8.(2分)(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
A.6B.3C.D.
解:如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,
\
结合图象可知,当点P在AO上运动时,,
∴PB=PC,,
又∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∴△APB≌△APC(SSS),
∴∠BAO=∠CAO=30°,
当点P在OB上运动时,可知点P到达点B时的路程为,
∴OB=,即AO=OB=,
∴∠BAO=∠ABO=30°,
过点O作OD⊥AB,垂足为D,
∴AD=BD,则AD=AO•cs30°=3,
∴AB=AD+BD=6,
即等边三角形ABC的边长为6.
故选:A.
9.(2分)(2023•浙江)如图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A.B.
C.D.
解:当水的深度未超过球顶时,
水槽中能装水的部分的宽度由下到上由宽逐渐变窄,再变宽,
所以在匀速注水过程中,水的深度变化先从上升较慢变为较快,再变为较慢;
当水的深度超过球顶时,
水槽中能装水的部分宽度不再变化,
所以在匀速注水过程中,水的深度的上升速度不会发生变化.
综上,水的深度先上升较慢,再变快,然后变慢,最后匀速上升.
故选:D.
10.(2分)(2023•大庆)如图1,在平行四边形ABCD中,∠ABC=120°,已知点P在边AB上,以1m/s的速度从点A向点B运动,点Q在边BC上,以m/s的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处,此时两点都停止运动.图2是△BPQ的面积y(m2)与点P的运动时间t(s)之间的函数关系图象(点M为图象的最高点),则平行四边形ABCD的面积为( )
A.12m2B.12m2C.24m2D.24m2
解:由题意可知:AB:BC=1:,设AB=a,则BC=,
如图,过点P作PE垂直于CB的延长线于点E,
∵PA=t,则PB=a﹣t,BQ=,
在Rt△PBE中,∠PBE=180°﹣∠ABC=60°,
∴PE=,
则y=,化简得:y=.
由二次函数图象可知,函数的顶点纵坐标为3,
∴==3,
∴a2=16,
∵a为正数,
∴a=4,
∴AB=4,则BC=,
如图,过点A作AF垂直于CB的延长线于点F,
在Rt△ABF中,∠ABF=60°,
∴AF==,
∴S▱ABCD=BC×AF==24 (m2).
故答案为:C.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023•西藏)函数中自变量x的取值范围是 x≠5 .
解:由题意可得:x﹣5≠0,
即x≠5,
故答案为:x≠5.
12.(2分)(2023•黑龙江)在函数y=中,自变量x的取值范围是 x≥﹣3 .
解:根据题意得:x+3≥0,解得:x≥﹣3.
故答案为:x≥﹣3.
13.(2分)(2023•衢州)在如图所示的方格纸上建立适当的平面直角坐标系,若点A的坐标为(0,1),点B的坐标为(2,2),则点C的坐标为 (1,3) .
解:如图:由A的坐标为(0,1),点B的坐标为(2,2),坐标可确定原点位置和坐标系:由图可得C(1,3),故答案为:(1,3).
14.(2分)(2023•巴中)已知a为正整数,点P(4,2﹣a)在第一象限中,则a= 1 .
解:∵点P(4,2﹣a)在第一象限,
∴2﹣a>0,
∴a<2,
又a为正整数,
∴a=1.
故答案为:1.
15.(2分)(2023•广安)函数y=的自变量x的取值范围是 x≥﹣2且x≠1 .
解:根据题意得:,
解得:x≥﹣2且x≠1.
故答案为:x≥﹣2且x≠1.
16.(2分)(2023•齐齐哈尔)如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,连接AB,过点O作OA1⊥AB于点A1,过点A1作A1B1⊥x轴于点B1;过点B1作B1A2⊥AB于点A2,过点A2作A2B2⊥x轴于点B2;过点B2作B2A3⊥AB于点A3,过点A3作A3B3⊥x轴于点B3;…;按照如此规律操作下去,则点A2023的坐标为 (4﹣,) .
解:在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,
∴△OAB 是等腰直角三角形,∠OBA=45°,
∵OA1⊥AB,
∴△OA1B 是等腰直角三角形,
同理可得:△OA1B1,△A1B1B均为等腰直角三角形,
∴A1(2,2),
根据图中所有的三角形均为等腰直角三角形,依次可得:A2(3,1),A3(4﹣,),A4(4﹣,),
由此可推出:点A2023的坐标为(4﹣,),
故答案为:(4﹣,).
17.(2分)(2022•钢城区)规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它绕原点顺时针旋转90°,由数字0和1组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点O(0,0)按序列“011…”作变换,表示点O先向右平移一个单位得到O1(1,0),再将O1(1,0)绕原点顺时针旋转90°得到O2(0,﹣1),再将O2(0,﹣1)绕原点顺时针旋转90°得到O3(﹣1,0)…依次类推.点(0,1)经过“011011011”变换后得到点的坐标为 (﹣1,﹣1) .
解:将点(0,1)经过一次011变换,
即先向右平移一个单位得到(1,1),
再绕点O顺时针旋转90得到(1,﹣1),
再绕点O顺时针旋转90得到(﹣1,﹣1);
如此将点(﹣1,﹣1)经过011变换得到点(0,1),
再将点(0,1)经过011变换得到点(﹣1,﹣1).
故答案为:(﹣1,﹣1).
18.(2分)(2023•烟台)如图1,在△ABC中,动点P从点A出发沿折线AB→BC→CA匀速运动至点A后停止.设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中点F为曲线DE的最低点,则△ABC的高CG的长为 .
解:如图过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+BQ=12时,点P到达点Q,此时当P在BC上运动时,AP最小,
∴BC=7,BQ=4,QC=3,
在Rt△ABQ中,AB=8,BQ=4,
∴AQ=,
∵S△ABC=AB×CG=AQ×BC,
∴CG=.
故答案为:.
19.(2分)(2023•贵州)如图,是贵阳市城市轨道交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,若贵阳北站的坐标是(﹣2,7),则龙洞堡机场的坐标是 (9,﹣4) .
解:由题中条件确定点O即为平面直角坐标系原点,
龙洞堡机场的坐标为(9,﹣4);
故答案为:(9,﹣4).
20.(2分)(2023•泰安)已知,△OA1A2,△A3A4A5,△A6A7A8,…都是边长为2的等边三角形,按如图所示摆放.点A2,A3,A5,…都在x轴正半轴上,且A2A3=A5A6=A8A9=…=1,则点A2023的坐标是 (2023,) .
解:如图,过点A1,A4,A7,A10,A13,……A2023分别作x轴的垂线,
∵△A1A2O是边长为2正三角形,
∴OB=BA2=1,A1B==,
∴点A1横坐标为1,
由题意可得,点A2横坐标为2,点A3横坐标为3,点A4横坐标为4,…
因此点A2023横坐标为2023,
∵2023÷3=674……1,而674是偶数,
∴点A2023在第一象限,
∴点A2023的纵坐标为,
即点A2023(2023,),
故答案为:(2023,).
三.解答题(共8小题,满分60分)
21.(6分)(2023•九龙坡区校级模拟)如图,在矩形ABCD中AB=3,BC=4.点E为CB中点,动点P从点E出发,沿折线E→C→D→C运动,当它回到点C时停止,设点P运动的路程为x,连接AP,PD.设三角形ADP的面积为y.
(1)求出y与x的函数关系式,并注明x的取值范围,在x的取值范围内画出y的函数图象;
(2)根据函数图象,写出该函数的一条性质;
(3)根据函数图象,直接写出当y=2时x的值.
解:(1)∵在矩形ABCD中,点E是BC的中点,BC=4,AB=3;
∴EC=BC=×4=2,AD=BC=4,DC=AB=3.
在矩形ABCD中,点P在EC之间移动时,△ADP底边AD上的高=矩形的宽AB=3;
点P在DC之间移动时,△ADP底边AD上的高=PD.
点P从E到C移动时,即0≤x≤2时,△ADP的面积y===6;
点P从C到D移动时,即2<x≤5时,△ADP的面积y===10﹣2x;
点P从D到C移动时,即5<x≤8时,△ADP的面积y===2x﹣10;
∴y=,
在x的取值范围内画出y的函数图象如图.
(2)根据图象可知:当0≤x≤2时,y不变;当2<x<5时,y随着x的增大而减小;当5≤x≤8时,y随着x的增大而增大.
(3)y=2时,x的值是4或6.
22.(6分)(2023•同心县模拟)如图是某片区平面示意图,超市的坐标是(﹣2,4),市场的坐标是(1,3).
(1)画出相应的平面直角坐标系;
(2)分别写出体育场、火车站和文化宫的坐标;
(3)若在(﹣3,﹣2)处建汽车站,在(2,﹣1)处建花坛,请在平面示意图中标出汽车站和花坛的位置.
解:(1)如图;
(2)由图可知,体育场(﹣4,2)、火车站(﹣1,1),文化宫(0,﹣2);
(3)汽车站和花坛的位置如图所示.
23.(8分)(2023•大连)如图1,在平面直角坐标系xOy中,点A,B分别在x轴和y轴上,直线AB与直线y=x相交于点C,点P是线段OA上一个动点(不与点A重合),过点P作x轴的垂线与直线AB相交于点D.设点P的横坐标为t.△DPA与△COA重叠部分的面积为S.S关于t的函数图象如图2所示(其中0≤t<m与m≤t<4时,函数的解析式不同).
(1)点A的坐标是 (4,0) ,△COA的面积是 .
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
解:(1)如图1,设PD交OC于点C,
从图2知,OA=4,即点A(4,0),
当点D和点B重合时,S=S△AOC=;
故答案为:(4,0),;
(2)S=S△AOC==AO•yC=2yC,
则yC=,
则点C(,),则m=,
由点A、C的坐标得,直线AC的表达式为:y=﹣x+2,
则点B(0,2);
由直线AC的表达式知,tan∠BOA=;
当≤t<4时,
则S=AP×PD=AP×PA•tan∠BOA=(4﹣t)2×=(t﹣4)2;
当0≤t<时,
如图1,则S=S△OCA﹣S△OPH=﹣PH•OP=﹣t2,
则S=.
24.(8分)(2023•永州)小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如表的一组数据:
(1)探究:根据上表中的数据,请判断和y=kt+b(k,b为常数)哪一个能正确反映总水量y与时间t的函数关系?并求出y关于t的表达式;
(2)应用:
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升?
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
解:(1)根据上表中的数据,y=kt+b(k,b为常数)能正确反映总水量y与时间t的函数关系,
∵当t=1时,y=7,当t=2时,y=12,
∴,
∴,
∴y=5t+2;
(2)①当t=20时,y=100+2=102,
即估算小明在第20分钟测量时量筒的总水量是102毫升;
②当t=24×60=1440分钟时,y=5×1440+2=7202(毫升),
当t=0时,y=2,
∴=144(天),
答:估算这个水龙头一个月(按30天计)的漏水量可供一人饮用144天.
25.(8分)(2023•怀远县校级模拟)如图(1),是边长为1的正方形OBB1C,以对角线OB1为一边作第2个正方形OB1B2C1,再以对角线OB2为一边作第3个正方形OB2B3C2,…依次下去,则:
(1)第2个正方形的边长= ,第10个正方形的边长= ()9 ,第n个正方形的边长为 ()n﹣1 .
(2)如图(2)所示,若以O为坐标原点,OC所在直线为x轴,OB所在直线为y轴,则点B3的坐标是 (2,﹣2) ,点B5的坐标是 (﹣4,﹣4) ,点B2014的坐标是 (﹣21007,0) .
解:(1)∵第1个正方形的边长为1,
∴由勾股定理可以得出:
第2个正方形的边长为:OB1==,
第3个正方形的边长为:2=()2,
第4个正方形的边长为:2=()3,
第5个正方形的边长为:4=()4,
…
第10个正方形的边长为:()9,
第 n个正方形的边长为:()n﹣1;
故答案为:,,()n﹣1;
(2)根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以,
∵从B到B3经过了3次变化,
∵45°×3=135°,1×()3=2.
∴点B3所在的正方形的边长为2,点B3位置在第四象限.
∴点B3的坐标是(2,﹣2);
可得出:B1点坐标为(1,1),
B2点坐标为(2,0),
B3点坐标为(2,﹣2),
B4点坐标为(0,﹣4),
B5点坐标为(﹣4,﹣4),
B6(﹣8,0),
B7(﹣8,8),
B8(0,16),
B9(16,16),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,
∵2014÷8=251…6,
∴从B到B2014与B6都在x轴负半轴上,
∴()2014=21007,
∴点B2014的坐标是(﹣21007,0).
故答案为:(2,﹣2),(﹣4,﹣4),(﹣21007,0).
26.(8分)(2023•靖江市模拟)如图1,已知∠MQN,QA、QB分别从QM、QN同时开始旋转,QA按逆时针方向旋转,旋转到与QN重合时停止旋转,QB按顺时针方向旋转,旋转到与QM重合后,立刻按原速度逆时针返回,与QN重合停止旋转.根据观察,QA、QB最终同时停止旋转,旋转过程中∠AQB的大小记作y(°),旋转时间记作t(s),y与t之间的关系如图2所示.
(1)依据图象,请直接填写:∠MQN= 120 °;QA旋转的速度是 °/s;a+b= 27秒 ;
(2)当∠AQB=40°时,求旋转时间t的值.
解:(1)根据图象,y轴上的点是120°,是最大值,也就是没运动时的角度,
所以∠MQN=120°.
观察图象得到运动6秒时,QA,QB两条线重合,所以VQA+VQB==20°/s,
因为在最终停止运动,QB运动两个路程,QA运动一个路程,
所以VQB=2VQA,
VQA=(VQB+VQA)=°/s,
当运动a秒时,QB到QM,
所以a=120÷=9(秒),
当运动b秒时,QB运动到QM,又返回到QN,
所以b=(120×2)÷=18(秒),
即a+b=27(秒).
故答案为:120°,°/s,27秒.
(2)当QA、QB未相遇时,
t=(120﹣40)÷20=4(秒),
当QA、QB相遇后,QB没到QM时,
t=(120+40)÷20=8(秒)
当QA、QB相遇后,且QB到达过QM,
t﹣(t﹣120)=40,
解得t=12,
所以当AOB=40时,t=4s,t=8s,t=12s.
27.(8分)(2023•庆云县模拟)我们在研究一个新函数时,常常会借助图象研究新函数的性质,在经历列表、描点、连线的步骤后,就可以得到函数图象,利用此方法对函数 y=﹣(|x|﹣2)2 进行探究.
[绘制图象]
(1)填写下面的表格,并且在平面直角坐标系中描出各点,画出该函数的图象.
[观察探究]
(2)结合图象,写出该函数的一条性质: 函数图象关于y轴对称(答案不唯一) ;
(3)方程﹣(|x|﹣2)2=﹣1的解是 x=﹣3或x=﹣1或x=1或x=3 ;
(4)若关于x的方程﹣(|x|﹣2)2=x+b有两个不相等的实数解,则b的取值范围是 b<﹣4或﹣ .
[延伸思考]
(5)将该函数的图象经过怎样的变换可以得到函数为y2=﹣(|x﹣1|﹣2)2+3的图象?写出变换过程,并直接写出当2<y2≤3时,自变量X的取值范围.
解:(1)如图所示;
(2)由图象知:函数图象关于y轴对称(答案不唯一),
故答案为:函数图象关于y轴对称(答案不唯一);
(3)方程﹣(|x|﹣2)2=﹣1的解为x=﹣3或x=﹣1或x=1或x=3,
故答案为:x=﹣3或x=﹣1或x=1或x=3;
(4)由图象知,b<﹣4时,直线y=x+b与图象y=﹣(|x|﹣2)2有两个交点,
当﹣(x﹣2)2=x+b有两个相等的实数根时,则x2﹣3x+4+b=0,
∴Δ=(﹣3)2﹣4(4+b)=0,
∴b=﹣,
当﹣(x+2)2=x+b有两个相等的实数根时,则x2+5x+4+b=0,
∴Δ=52﹣4(4+b)=0,
∴b=,
∴方程﹣(|x|﹣2)2=x+b有两个不相等的实数解时,b<﹣4或﹣,
故答案为:b<﹣4或﹣;
(5)将函数y=﹣(|x|﹣2)2向右平移1个单位,再向上平移3个单位可得函数y2=﹣(|x﹣1|﹣2)2+3的图象,
当2<﹣(|x﹣1|﹣2)2+3≤3,
∴﹣1<﹣(|x﹣1|﹣2)2≤0,
∴﹣1<|x﹣1|﹣2<1,
∴1<|x﹣1|<3,
∴﹣3<x﹣1<﹣1或1<x﹣1<3,
∴﹣2<x<0或2<x<4.
28.(8分)(2023•七星区校级模拟)如图①,四边形ABCD中,AB∥CD,∠ADC=90°.
(1)动点M从A出发,以每秒1个单位的速度沿路线A→B→C→D运动到点D停止.设运动时间为a,△AMD的面积为S,S关于a的函数图象如图②所示,求AD、CD的长.
(2)如图③,动点P从点A出发,以每秒2个单位的速度沿路线A→D→C运动到点C停止.同时,动点Q从点C出发,以每秒5个单位的速度沿路线C→D→A运动到点A停止.设运动时间为t,当Q点运动到AD边上时,连接CP、CQ、PQ,当△CPQ的面积为8时,求t的值.
解:(1)由函数图象可知,点M从A出发,从点C到D耗时16秒,即CD=16,
此时S=CD•AD=16×AD=96,解得:AD=12,
∴AD=12,CD=16;
(2)由题意得,当Q运动到A停止的时间为,而点P运动到D的时间为=6,
当点P、Q都在AD边上,此时有以PQ为底边,CD为高的三角形CPQ,
设运动的时间为t,则AP=2t,DQ=5t﹣16,而≤t<,
当点P在Q上方时,则PQ=AD﹣AP﹣QD=12﹣2t﹣5t+16=28﹣7t,
△CPQ的面积=PQ×CD=(28﹣7t)×16=8,解得:t=(满足条件);
当点P在点Q下方时,PQ=DQ﹣(AD﹣AP)=5t﹣16﹣(12﹣2t)=7t﹣28,
△CPQ的面积=PQ×CD=(7t﹣28)×16=8,解得:t=(满足条件);
当点P在CD上时,点Q运动到A时,×(28﹣2t)×12=8,解得t=,
综上,t=或或
时间t
(单位:分钟)
1
2
3
4
5
…
总水量y
(单位:毫升)
7
12
17
22
27
…
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
Y=(|x|﹣2)2
…
…
专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题12反比例函数教师版docx、专题12反比例函数学生版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题13 二次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题13 二次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题13二次函数教师版docx、专题13二次函数学生版docx等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
专题11 一次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题11 一次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题11一次函数教师版docx、专题11一次函数学生版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。