初中数学湘教版九年级下册2.6 弧长与扇形面积示范课课件ppt

这是一份初中数学湘教版九年级下册2.6 弧长与扇形面积示范课课件ppt，共29页。PPT课件主要包含了半径和圆心角，弧长是弧的长度，Sπr2，温馨提示，等边三角形，旋转了120°，圆心角，弓形的面积公式，弓形所在的弧为劣弧时，弓形所在的弧为优弧时等内容，欢迎下载使用。

1.经历探索弧长计算公式和扇形面积计算公式的过程.2.会运用弧长计算公式和扇形面积的计算公式进行计算.
问题1 半径为r的圆，周长是多少？面积是多少？
问题2 什么是弧长？问题3 弧长和哪些量有关？
如图所示是一把圆弧形状的扇子的示意图,你能求出做这把扇子用了多少纸吗？
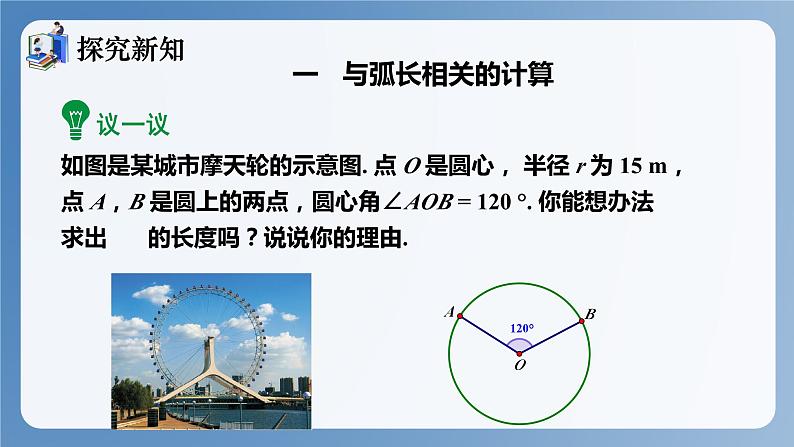
如图是某城市摩天轮的示意图. 点 O 是圆心， 半径 r 为 15 m， 点 A，B 是圆上的两点，圆心角∠AOB = 120 °. 你能想办法求出 的长度吗？说说你的理由.
一 与弧长相关的计算
如果∠AOB = n°，你能求出 的长吗？
在同圆或等圆中,如果圆心角相等, 那么它们所对的弧长_______.
1°的圆心角所对的弧长 l =_____ .
n°的圆心角所对的弧长 l =______ .
用弧长公式进行计算时，要注意公式中n的意义：n表示1°圆心角的倍数，它是不带单位的.
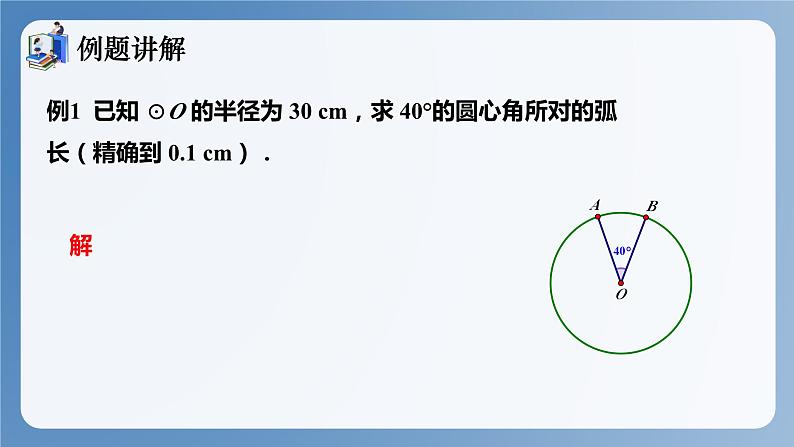
例1 已知 ⊙O 的半径为 30 cm，求 40°的圆心角所对的弧长（精确到 0.1 cm）．
例2 如图，一个边长为 10 cm 的等边三角形木板 ABC 在水平桌面上绕顶点 C 按顺时针方向旋转到△A′B′C 的位置，求顶点 A 从开始到结束所经过的路程为多少.
∠A′CB′ = 60°
∠ACA′ = 120°
点A经过的路程长等于 的长.
解：∵ 等边三角形 ABC 的边长为 10 cm，∴ 所在圆的半径为10 cm.∴答：顶点 A 从开始到结束时所经过的路程为 cm.
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
蓝色部分是一个扇形， 记作扇形 OAB．
我们可以发现，扇形面积与组成扇形的圆心角的大小有关，在同一个圆中，圆心角越大， 扇形面积也越大.
二 与弧长相关的计算
如何求半径为 r，圆心角为 n°的扇形的面积呢？
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为 r, 1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
如果设圆心角为n°的扇形的面积为S，圆的半径为r，那么扇形的面积为
公式中 n 的意义：n 表示 1° 圆心角的倍数，它是不带单位的；
比较扇形面积（ S ）公式和弧长（ l ）公式，你能用弧长来表示扇形的面积吗？
扇形的面积与哪些因素有关？
大小不变时，对应的扇形面积与 有关， 越长，面积越大.
圆的 不变时，扇形面积与 有关， 越大，面积越大.
总结：扇形的面积与圆心角、半径有关.
例1 如图，⊙O 的半径为 1.5 cm，圆心角∠AOB ＝ 58°，求扇形 OAB 的面积（精确到 0.1 cm2）．
解 ∵ r ＝ 1.5 cm ，n ＝ 58 ，
例2 如图,是一条圆弧形弯道，已知 OA ＝20 m，OC ＝ 12 m， 的长度为 9π m，求圆弧形弯道的面积.
解设∠AOB = n°，∵ OC = 12 m， 的长度为 9π m，∴ 解得 n = 135，即圆心角∠COD = 135 ° .∴∴S扇形ACDB = S扇形OAB - S扇形OCD = 150π - 54π = 96π（m2）答：这条圆弧形弯道的面积为 96π m2.
例3 如图，水平放置的圆柱形排水管道的截面半径是0.6 m，其中水面高 0.3 m，求截面上有水部分的面积（结果保留小数点后两位）．
解：如解图，连结OA，OB，作弦AB的垂直平分线，垂足为D，交弧AB于点C，连接AC.∵OC=0.6 m，DC=0.3 m，∴OD=OC-DC=0.3（m）.∴OD=DC.又AD⊥DC，∴AD是线段OC的垂直平分线.∴AC=AO=OC.
从而∠AOD=60°，∠AOB=120°.有水部分的面积
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
1.（2022浙江丽水）某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为2 m，高为2m，则改建后门洞的圆弧长是(　　)
A. m B. m C. m D. m
2. 如图，⊙A、 ⊙B、 ⊙C、 ⊙D 两两不相交，且半径都是 2 cm，则图中阴影部分的面积是 .
3. （山西中考）如图是某商品的标志图案, AC 与 BD是☉O 的两条直径,首尾顺次连接点 A , B , C , D ,得到四边形 ABCD ．若 AC ＝ 10 cm, ∠BAC ＝36°, 则图中阴影部分的面积为（ ）A. 5π cm2 B. 10π cm2C. 15π cm2 D. 20π cm2
4.如图是一个闹钟正面的内、外轮廓线．内轮廓线由一段圆弧和一条弦 AB 组成，圆心为 O，半径为3.2 cm，圆心角∠AOB＝ 83°，求内轮廓线的圆弧的长度．
n = 360°-83°= 277°
答：内轮廓线的圆弧长为 15.5 cm.
5.（2022黑龙江齐齐哈尔）如图，在△ABC中，AB＝AC，以AB为直径作⊙O，AC与⊙O交于点D，BC与⊙O交于点E，过点C作CF∥AB，且 CF＝CD，连接BF.(1)求证：BF是⊙O的切线；
(1)证明：如图，连接BD，∵AB是⊙O的直径，∴∠BDA＝90°，∴∠BDC＝90°，∵AB＝AC，∴∠ABC＝∠ACB.
6.（2022山东泰安）如图，四边形ABCD中，∠A＝60°，AB∥CD，DE⊥AD交AB于点E，以点E为圆心，DE为半径，且DE＝6的圆交CD于点F，则阴影部分的面积为(　　)
A. 6π－9B. 12π－9C. 6π－D. 12π－
S弓形=S扇形-S三角形S弓形=S扇形+S三角形
1.教材P81第1、2、3题. 2.完成同步练习册中本课时的练习.