




精品解析:+四川省遂宁市射洪市2023-2024学年七年级上学期期末考试数学试题
展开本试卷共150分.考试时间120分钟.
答卷前,考生务必将学校、姓名、准考证号填写和填涂在答题卡上.作答时,将选择题答案用2B铅笔填涂在答题卡上,试卷中注有“▲”的地方,需要你用0.5mm黑色签字笔在答题卡规定的地方作答;写在本试题卷上无效.考试结束后,将答题卡交回.
一、选择题:(每小题都有A、B、C、D四个选项,其中只有一个选项是正确的,每小题3分,共60分)
1. 同学们,我们是初中2023级的学生,数字2023的倒数是( )
A. 2023B. C. D.
【答案】B
【解析】
【分析】本题考查了倒数的定义,熟练掌握倒数的定义是解答本题的关键.乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数,正数的倒数是正数,负数的倒数是负数,0没有倒数.根据定义求解即可.
【详解】解:∵.
∴2023的倒数是.
故选B.
2. 在,0,,四个数中,最小的那个数是( )
A. B. 0C. D.
【答案】A
【解析】
【分析】本题考查的是有理数的大小比较.利用有理数大小比较的方法:正数都大于零,负数都小于零,正数大于负数;两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小;直接按顺序排列,选择答案即可.
【详解】解:∵,
∴四个数中,最小的数是,
故选:A.
3. 手机移动支付给生活带来便捷,如图是张老师2021年9月18日微信账单收支明细(正数表示收入,负数表示支出,单位:元),张老师当天微信收支的最终结果是( )
A. 收入19元B. 支出8元C. 支出5元D. 收入6元
【答案】D
【解析】
【分析】根据有理数的加法运算求解即可.
详解】根据题意,有:(元),
即张老师当天微信收支的最终结果是收入6元,
故选:D.
【点睛】本题主要考查了正负数的应用,有理数的加法运算,掌握正负数的实际意义,列出算式是解答本题的关键.
4. 2023年10月8日晚,伴随圣火缓缓熄灭,杭州第19届亚运会圆满闭幕.亚运是体育盛会,也是文化旅游的盛会.在刚刚过去的中秋国庆假期,杭州市消费总金额约为237亿元.将237亿元用科学记数法表示为( )
A. 元B. 元
C. 元D. 元
【答案】A
【解析】
【分析】本题考查了科学记数法的表示方法,科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【详解】解:,
故选:A.
5. -a、b两数在数轴上的位置如图,下列结论正确的是( )
A. a>0,b<0B. a<b
C. , D. >
【答案】C
【解析】
【分析】先由数轴上a,b两点的位置确定a,b的符号,及绝对值的大小,即可求解.
【详解】根据数轴得到,且,
∴,
A、,,故该选项错误;
B、,故该选项错误;
C、,,故该选项正确;
D、,故该选项错误;
故选:C.
【点睛】本题考查了数轴,根据点在数轴上的位置判断式子的正负,数轴上的数右边的数总是大于左边的数的特点.
6. 已知点M在数轴上表示的数是-4,点N与点M的距离是3,则点N表示的数是( )
A. -1B. -7C. -1或-7D. -1或1
【答案】C
【解析】
【分析】在数轴上与表示-4的点距离是4个单位长度的点有两个,一个在表示点M的左边3个单位长度,一个在点M的右边3个单位长度,由此求得答案即可.
【详解】解:在数轴上与表示-4的点距离是3个单位长度的点所表示的数是-4-3=-7或-4+3=-1.
∴点N表示的数是-7或-1.
故选:C.
【点睛】此题考查数轴上两点间的距离,分类探讨是解决问题的关键.
7. 下列代数式中符合书写要求的是( )
A. B. C. D.
【答案】D
【解析】
【详解】解:A. ,故原选项不合题意;
B. ,故原选项不合题意;
C. ,故原选项不合题意;
D. 符合书写要求,符合题意.
故选:D
8. 下列计算正确的是( )
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查了合并同类项,在合并同类项时,只对同类项的系数进行相加减,字母部分保持不变.
【详解】解:A、,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、与不是同类项,不能合并,原式计算错误,不符合题意;
D、,原式计算正确,符合题意;
故选D.
9. 下列判断大小正确的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】此题考查了有理数比较大小,准确利用绝对值和符号法则化简各数是解题的关键.
【详解】解:A.则,故选项正确,符合题意;
B.,则,故选项错误,不符合题意;
C.,∵,∴,故选项错误,不符合题意;
D.,则,故选项错误,不符合题意.
故选:A.
10. 如果与是同类项,则的值为( )
A. 4B. C. 8D. 12
【答案】B
【解析】
【分析】根据所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项,得出m,n的值,进而得出答案.
【详解】解:∵与是同类项,
∴,
∴,
∴.
故选:B.
【点睛】本题主要考查的是同类项的定义,熟练掌握同类项的概念是解题的关键.
11. 为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共200本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本.设购买甲种读本x本,则购买乙种读本的费用为( )
A. 元B. 元
C. 元D. 元
【答案】B
【解析】
【分析】本题主要考查列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.根据乙种读本的单价×乙种读本的数量列式即可得出答案.
【详解】解:根据题意知,购买甲种读本x本,
则购买乙种读本的费用为元,
故选:B.
12. 若代数式的值与的取值无关,则的值为( )
A. B. 1C. 0D. 2
【答案】D
【解析】
【分析】本题考查了整式的加减即化简求值问题,原式去括号合并后,根据结果与的取值无关,得到的值,代入式子计算即可,熟练掌握运算法则是解题的关键.
【详解】解:
=
=
=,
∵与的取值无关,
∴,解得,
∴,
故选:D.
13. 下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
【分析】根据三视图的定义、结合图形对各个几何体进行观察即可判断.
【详解】正方体从前往后看和从上往下看,看到的图形形状都是正方形,①符合题意;
球从前往后看和从上往下看,看到的图形形状都是圆,②符合题意;
圆锥从前往后看和从上往下看,看到的图形形状分别是三角形和圆,③不合题意;
圆柱从前往后看和从上往下看,看到的图形形状分别是矩形和圆,④不合题意,
故选B.
【点睛】本题考查的是简单几何体的三视图,理解三视图的概念、正确观察图形是解题的关键.
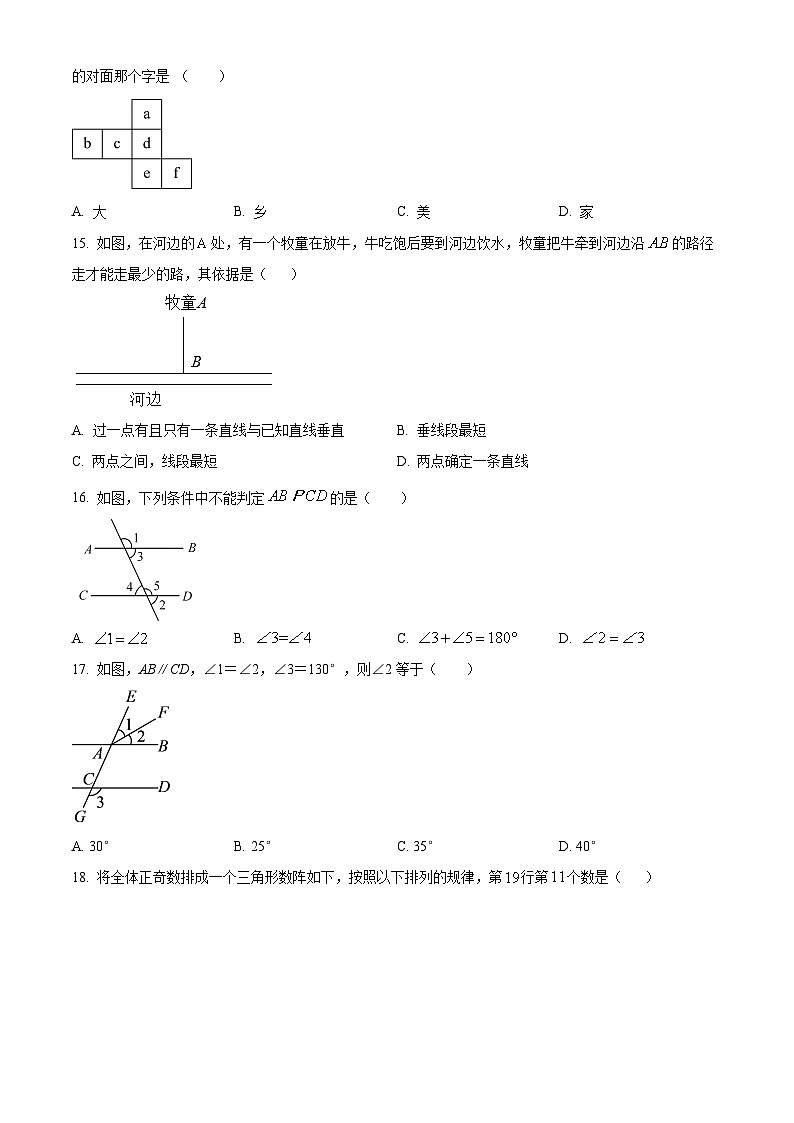
14. 下图是正方体的表面展开图,上面字母“”分别对应写有“我爱大美家乡”六个字,则“爱”的对面那个字是 ( )
A. 大B. 乡C. 美D. 家
【答案】C
【解析】
【分析】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“a”与“e”是相对面,
“b”与“d”是相对面,
“c”与“f”是相对面.
∵字母“”分别对应写有“我爱大美家乡”六个字,
∴“b”对应爱,“d”对应美,
∴“爱”的对面那个字是美,
故选:C.
15. 如图,在河边的处,有一个牧童在放牛,牛吃饱后要到河边饮水,牧童把牛牵到河边沿的路径走才能走最少的路,其依据是( )
A. 过一点有且只有一条直线与已知直线垂直B. 垂线段最短
C. 两点之间,线段最短D. 两点确定一条直线
【答案】B
【解析】
【分析】根据题意可直接进行求解.
【详解】解:由题意可把河边看作一条直线,则牧童把牛牵到河边沿的路径走才能走最少的路,其依据是点到直线,垂线段最短;
故选B.
【点睛】本题主要考查垂线段最短,熟练掌握点到直线,垂线段最短是解题的关键.
16. 如图,下列条件中不能判定的是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据平行线的判定逐项判断即可.
【详解】解:A、∵,
∴,不能判定,则此项符合题意;
B、∵,
∴(内错角相等,两直线平行),则此项不符合题意;
C、∵,
∴(同旁内角互补,两直线平行),则此项不符合题意;
D、∵,
∴(同位角相等,两直线平行),则此项不符合题意;
故选:A.
【点睛】本题考查了平行线的判定,能灵活运用平行线的判定进行推理是解题关键.
17. 如图,AB∥CD,∠1=∠2,∠3=130°,则∠2等于( )
A. 30°B. 25°C. 35°D. 40°
【答案】B
【解析】
【分析】根据AB∥CD,∠3=130°,求得∠GAB=∠3=130°,利用平行线的性质求得∠BAE=180°﹣∠GAB=180°﹣130°=50°,由∠1=∠2 求出答案即可.
【详解】解:∵AB∥CD,∠3=130°,
∴∠GAB=∠3=130°,
∵∠BAE+∠GAB=180°,
∴∠BAE=180°﹣∠GAB=180°﹣130°=50°,
∵∠1=∠2,
∴∠2=∠BAE=×50°=25°.
故选:B.
【点睛】此题考查平行线的性质:两直线平行同位角相等,两直线平行同旁内角互补,熟记性质定理是解题的关键.
18. 将全体正奇数排成一个三角形数阵如下,按照以下排列的规律,第行第个数是( )
A. B. C. D.
【答案】A
【解析】
【分析】先找出每一行第一个数的变化规律,即可求出第行第个数.
【详解】解:第1行第1个数为:1=12;
第2行第1个数为:3=22-1;
第3行第1个数为:7=32-2;
第4行第1个数为:13=42-3;
第n行第1个数为:n2-(n-1),
∴第19行第1个数为:192-18=343
∴第19行第11个数为:343+(11-1)×2=363.
故选A.
【点睛】此题考查的是数字规律题,找出每一行第一个数的变化规律是解决此题的关键.
19. 规定符号表示a,b两个数中较小的一个,规定符号表示两个数中较大的一个,例如,,则的结果为( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了新定义,有理数的大小比较,以及整式的加减,根据题意得出和的值是解题的关键.
【详解】解:
,
故选B.
20. 如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点;第二次操作:分别取线段和的中点;第三次操作:分别取线段和的中点;……连续这样操作10次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
【答案】A
【解析】
【分析】根据,分别为的中点,求出的长度,再由的长度求出的长度,找到的规律即可求出的值.
【详解】解:∵,分别为的中点,
∴,
∵分别为的中点,
∴,
根据规律得到,
∴,故选A.
【点睛】本题是对线段规律性问题的考查,准确根据题意找出规律是解决本题的关键,相对较难.
二、填空题:(请把答案填在答题卡上,每空3分,共30分)
21. 用代数式表示:x的2倍与y的平方的差___________.
【答案】
【解析】
【分析】根据“x的2倍即2x,再表示与y的平方的差”可列出代数式.
【详解】解:根据题意得;2x-y2.
故答案为:.
【点睛】本题考查列代数式,关键根据语句的描述理解代数式中的运算顺序,从而得到代数式.
22. 在中,非负整数的个数为______.
【答案】3
【解析】
【分析】本题考查有理数的分类,根据非负整数包括:正整数和0,进行判断即可.
【详解】解:中,非负整数有,共3个;
故答案为:3.
23. 把多项式按照的降幂排列是____.
【答案】
【解析】
【分析】本题考查了多项式的重新排列,我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列,称为按这个字母的降幂或升幂排列.根据x的指数从大到小排列即可.
【详解】解:
.
24. 若,则__________.
【答案】
【解析】
【分析】根据几个非负数的和为零,则每个非负数均为零求出的值,再代入求值即可.
【详解】∵,,,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查了非负数的性质,代入求值,熟练掌握知识点是解题的关键.
25. 若,则的补角的度数为______.
【答案】
【解析】
【分析】本题主要考查了求一个角的补角,解题的关键是熟练掌握互为补角的两个角和为.
【详解】解:,
即的补角的度数为.
故答案:.
26. 当,时,代数式的值为____.
【答案】
【解析】
【分析】此题考查了整式加减的化简求值,先去括号并合并同类项后,把字母的值代入化简结果计算即可.
【详解】解:
当,时,
原式
故答案为:
27. 如图,是一段高铁行驶路线图,图中字母表示的5个点表示5个车站,在这段路线上往返行车,需印制________种车票.
【答案】20
【解析】
【分析】本题考查线段的数量问题,根据图形求得线段个数即可求解.
【详解】解:根据题意,这段路线有10条线段,
∴在这段路线上往返行车,需印制种车票,
故答案为:20.
28. 已知的值为4,则代数式的值为____.
【答案】0
【解析】
【分析】此题考查了求代数式的值,根据题意可得,再整体代入变形后得到的代数式即可得到答案.
【详解】解:∵的值为4,
∴,
∴
故答案为:0
29. 一个几何体由一些大小相同的小正方体组成,如图是它的主视图、左视图和俯视图,那么组成该几何体所需小正方体的个数是____.
【答案】6
【解析】
【分析】本题主要考查了从不同的方向看几何体,根据三个方向看到的图形确定每个位置的小立方体数即可得到答案.
【详解】解:由三视图可知,在俯视图中每个位置的小正方体数如下所示:
∴一共需要小正方体的个数是,
故答案为:6.
30. 如图,,点在上,,平分,且平分.下列结论:①;②;③;④;其中正确的是____.(请填写序号)
【答案】①②③④
【解析】
【分析】本题考查了平行线的判定与性质,角平分线的定义等知识,熟练掌握平行线的判定与性质是解题的关键.①根据角平分线的定义得出,,再根据,即可得出,于是推出;②由角平分线的定义结合已知推出,再根据内错角相等,两直线平行即可得出;③由两直线平行,内错角相等得出,结合角平分线的定义得出,结合①的结论即可得出;④先证,再根据平行线的性质即可得证.
【详解】解:平分,
,
平分,
,
,
,
,
即,
故①正确;
平分,
,
,
,
,
故②正确;
平分,
,
,
,
,
由①知,
,
故③正确;
平分,
,
,
,
,
,
故④正确.
其中正确的有:①②③④,
故答案为:①②③④.
三、计算或解答题:(共60分)
31. 计算
(1);
(2);
(3);
(4).
【答案】(1)11 (2)
(3)50 (4)3
【解析】
【分析】此题考查了有理数的混合运算,熟练掌握有理数的运算法则和运算顺序是解题的关键.
(1)先计算乘法,再计算减法即可;
(2)先计算乘方、除法、乘法,最后计算加法即可;
(3)逆用乘法分配律进行计算即可;
(4)除法变乘法后,利用乘法分配律进行计算即可.
【小问1详解】
;
【小问2详解】
;
【小问3详解】
=
=
【小问4详解】
=
32. 先化简,再求值,其中,.
【答案】,
【解析】
【分析】本题考查了整式加减的化简求值,熟练掌握整式加减的化简求值时解题的关键.先去括号,然后合并同类项,得到化简结果,再将,代入计算,即得答案.
【详解】原式
,
当,时,
原式.
33. 已知代数式,马小虎同学在做整式加减运算时,误将“”看成“”了,计算的结果是.
(1)请你帮马小虎同学求出正确的结果;
(2)x是最大的负整数,将x代入(1)问的结果求值.
【答案】(1)
(2)18
【解析】
【分析】(1)根据题意可得进行计算即可得到B的值,再计算即可;
(2)根据题意可得为最大的负整数,则,再将其代入即可求出解答.
【小问1详解】
由题意可得,
,
∴
.
【小问2详解】
由题意可得为最大的负整数,
∴,
∴当时,
.
【点睛】本题主要考查整式的加减混合运算,掌握整式的加减混合运算法则是解题的关键.
34. 如图,在中,平分,过点D作交CB于点E,过点E作交于点F,则可推得平分,其推导过程和推理依据如下:
解:∵,(已知)
∴ .( )
又∵,(已知)
∴ , ( )
( )
∴.(等量代换)
又∵平分,(已知)
∴.( )
∴ .(等量代换)
∴平分.(角平分线定义)
请完善以上推导过程和推理依据,并按照顺序将相应内容填写在答题卡指定区域内.
【答案】;两直线平行,内错角相等;;两直线平行,内错角相等;;两直线平行,同位角相等;角平分线定义;
【解析】
【分析】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.根据平行线的性质及角平分线定义求解即可.
【详解】解:∵(已知)
∴(两直线平行,内错角相等)
∵(已知)
∴(两直线平行,内错角相等)
(两直线平行,同位角相等)
∴(等量代换)
又∵平分(已知)
∴(角平分线定义)
∴(等量代换)
∴平分.(角平分线定义)
故答案为:;两直线平行,内错角相等;;两直线平行,内错角相等;;两直线平行,同位角相等;角平分线定义;.
35. 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的.如下所示是该市自来水收费价格见价目表.
(1)填空:若该户居民2月份用水,则应收水费 元;
(2)若该户居民3月份用水(其中),则应收水费多少元?(用的整式表示并化简)
(3)若该户居民4,5月份共用水(5月份用水量超过了4月份),设4月份用水,求该户居民4,5月份共交水费多少元?(用整式表示并化简)
【答案】(1)8 (2)元
(3)4,5月份交的水费为元或元或36元
【解析】
【分析】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
(1)根据表格中的收费标准,求出水费即可;
(2)根据a的范围,求出水费即可;
(3)根据5月份用水量超过了4月份,得到4月份用水量少于,当4月份的用水量少于时,5月份用水量超过;4月份用水量不低于,但不超过时,5月份用水量不少于,但不超过;4月份用水量超过,但少于时,5月份用水量超过但少于三种情况分别求出水费即可.
【小问1详解】
根据题意得:(元);
【小问2详解】
根据题意得:(元);
【小问3详解】
由5月份用水量超过了4月份,得到4月份用水量少于,
当4月份用水量少于时,5月份用水量超过,
则4,5月份共交水费为(元);
当4月份用水量不低于,但不超过时,5月份用水量不少于,但不超过,
则4,5月份交的水费为(元);
当4月份用水量超过,但少于时,5月份用水量超过但少于,
则4,5月份交的水费为(元).
综上所述,4,5月份交的水费为元或元或36元.
36. 如图,直线,直线与分别交于点G,H,.小明将一个直角三角形按如图①放置,使点N、M分别在直线上,且在点C、H的右侧,.
(1)填空: 度;
(2)若的平分线交直线于点O,如图②.
①当时,求α的度数;
②小明将三角形沿直线左右移动,保持,点N、M分别在直线和直线上移动,请直接写出的度数(用含α的式子表示).
【答案】(1)90 (2)①;②或
【解析】
【分析】本题主要考查平行线的性质,角平分线的定义,分类讨论是解题的关键.
(1)过P点作,根据平行线的性质可得,,进而可求解;
(2)①由平行线的性质可得,结合角平分线的定义可得,再利用平行线的性质可求解;
②可分两种情况:点N在G的右侧时,点N在G的左侧时,利用平行线的性质及角平分线的定义计算可求解.
【小问1详解】
过P点作,
∴,
∵,
∴,
∴,
∴,
故答案为:(或);
【小问2详解】
①∵,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴;
②点N在G的右侧时,如图②,
∵,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴;
点N在G的左侧时,如图,
∵,
∴,
∴,
∵,
∴,
∵平分,
∴,
∴,
综上所述,的度数为或.价目表
每月用水量
单价
不超出的部分
2元
超出但不超出的部分
4元
超出的部分
8元
注:水费按月结算.
四川省遂宁市射洪市四川省射洪中学校2023-2024学年八年级上学期11月期中数学试题: 这是一份四川省遂宁市射洪市四川省射洪中学校2023-2024学年八年级上学期11月期中数学试题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省遂宁市射洪市四川省射洪中学校2023-2024学年七年级上学期11月期中数学试题: 这是一份四川省遂宁市射洪市四川省射洪中学校2023-2024学年七年级上学期11月期中数学试题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省遂宁市射洪中学校2023—2024学年九年级上学期11月期中数学试题: 这是一份四川省遂宁市射洪中学校2023—2024学年九年级上学期11月期中数学试题,共8页。试卷主要包含了已知下列各式,代数式有意义的的取值范围是,设,,则下列运算中错误的是,把方程的左边配方后可得方程,方程,则的值是等内容,欢迎下载使用。












