山东省青岛市平度市、胶州市、黄岛区2023-2024学年九年级上学期期末数学试题(含答案)

这是一份山东省青岛市平度市、胶州市、黄岛区2023-2024学年九年级上学期期末数学试题(含答案)，共14页。试卷主要包含了已知，则下列各式不一定成立的是，在中，，，则的形状等内容，欢迎下载使用。

（考试时间：120分钟；满分120分）
说明：
1．本试题分第I卷和第Ⅱ卷两部分，共25题．第I卷为选择题，共10小题，30分；第Ⅱ卷为填空题、作图题、解答题，共15小题，90分．
2．所有题目均在答题卡上作答，在试题上作答无效．
第I卷（共30分）
一、选择题（本大题共10小题，每小题3分，共30分）
在每个题给出的四个选项中，只有一项是符合题目要求的．
1．如图是一把做工精湛的紫砂壶，其俯视图的大致形状是（ ）
（第1题）
A．B．C．D．
2．2024年1月4日，第22届瓦萨国际滑雪节开幕式在长春净月潭国家森林公园启幕．如图，一名滑雪运动员沿着倾斜角为的斜坡，从点滑行到点，若，则这名滑雪运动员下降的高度为（ ）
（第2题）
A．B．C．D．
3．小明拿一个等边三角形木框在阳光下玩，等边三角形木框在地上的投影不可能是（ ）
A．一个点B．线段C．等腰三角形D．等边三角形
4．如图是一把直角三角尺，，，，，且，则这把三角尺中与的周长比为（ ）
（第4题）
A．7：5B．49：25C．14：5D．196：25
5．已知，则下列各式不一定成立的是（ ）
A．B．C．D．
6．若点是二次函数图象的最低点，则点的坐标是（ ）
A．B．C．D．
7．在中，，，则的形状（ ）
A．一定是锐角三角形B．一定是直角三角形
C．一定是钝角三角形D．无法确定
8．已知线段，，，，则下列图形中线段的数量关系能得到的是（ ）
A．B．C．D．
9．如图，在一个长为80m，宽为50m的矩形停车场中有四块相同的矩形停车区域，它们的面积之和为，四块停车区域之间以及周边留有宽度相同的行车通道，如果设行车通道的宽度为，那么列出的方程为（ ）
（第9题）
A．B．
C．D．
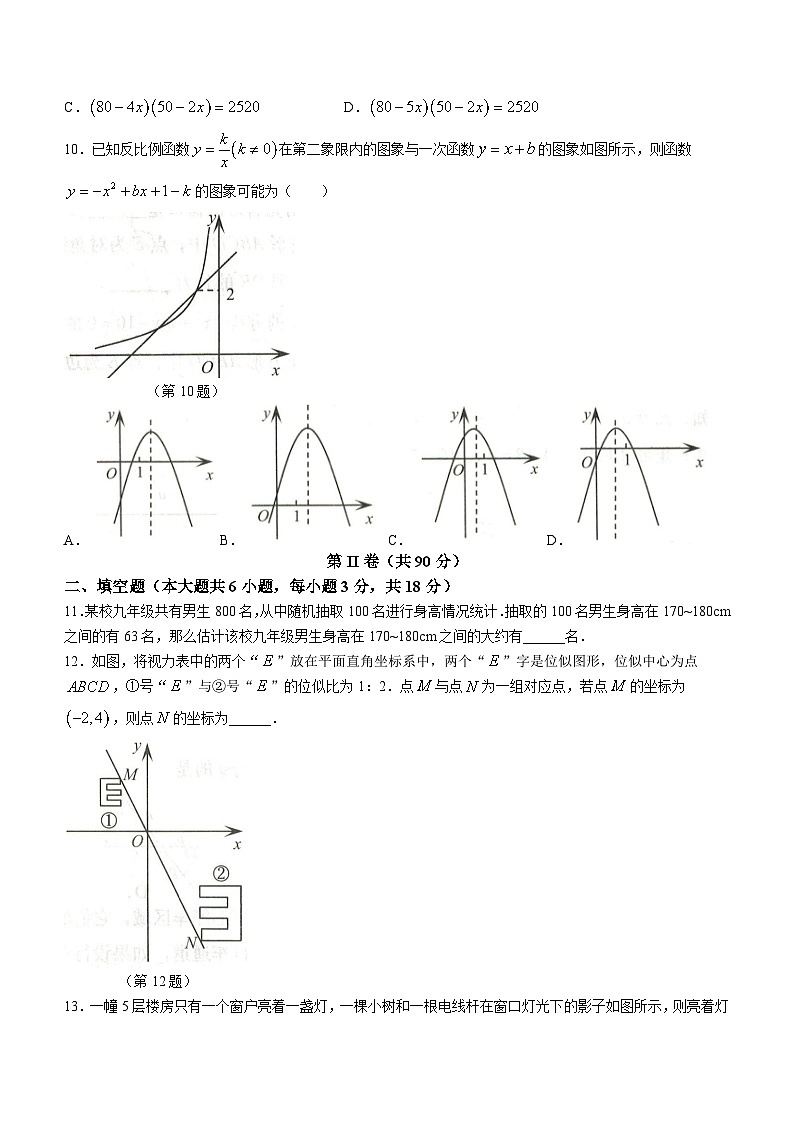
10．已知反比例函数在第二象限内的图象与一次函数的图象如图所示，则函数的图象可能为（ ）
（第10题）
A．B．C．D．
第II卷（共90分）
二、填空题（本大题共6小题，每小题3分，共18分）
11．某校九年级共有男生800名，从中随机抽取100名进行身高情况统计．抽取的100名男生身高在170~180cm之间的有63名，那么估计该校九年级男生身高在170~180cm之间的大约有______名．
12．如图，将视力表中的两个“”放在平面直角坐标系中，两个“”字是位似图形，位似中心为点，①号“”与②号“”的位似比为1：2．点与点为一组对应点，若点的坐标为，则点的坐标为______．
（第12题）
13．一幢5层楼房只有一个窗户亮着一盏灯，一棵小树和一根电线杆在窗口灯光下的影子如图所示，则亮着灯的窗口是______．（填写相应的数字序号即可）
（第13题）
14．如图，在菱形中，点为对角线上一点，且，连接，若，，则的长为______．
（第14题）
15．已知关于的方程的一个根是5，则它的另一个根是______．
16．如图，在正方形中，点为边的中点，交于点，过点作于点，则=______．
（第16题）
三、作图题（本题满分4分）
请用直尺、圆规作图，不写作法，但要保留作图痕迹．
17．已知：线段．
（第17题）
求作：矩形，使得，．
四、解答题（本大题共8小题，共68分）
18．（本题满分8分，每小题4分）
（1）解方程：．
（2）已知关于的一元二次方程有实数根，求的取值范围．
19．（本题满分6分）
杭州亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人，组合名为“江南忆”，出自唐朝诗人白居易的名句“江南忆，最忆是杭州”，它融合了杭州的历史人文、自然生态和创新基因．现有三张不透明的卡片，其正面图案分别为杭州亚运会吉祥物“宸宸”、“琮琮”、“莲莲”图案（卡片依次记为，，），卡片除正面图案不同外，其余均相同．现将这三张卡片背面向上洗匀，从中随机抽取一张，记录图案后放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求两次抽出的卡片上的图案都是“宸宸”的概率．
（第19题）
20．（本题满分8分）
如图，某小区有南北两个门，北门在南门的正北方向，小红自小区北门处出发，沿南偏西．53°方向前往小区居民活动中心处；小强自南门处出发，沿正西方向行走300m到达处，再沿北偏西30°方向前往小区居民活动中心处与小红汇合，两人所走的路程相同，求该小区北门与南门之间的距离．（结果保留整数，参考数据：，，，）
（第20题）
21．（本题满分8分）
如图，一次函数的图象与反比例函数的图象相交于点和点，与轴交于点，与轴交于点．
（第21题）
（1）求反比例函数与一次函数的关系式；
（2）根据图象直接写出的解集．
22．（本题满分8分）
在探究图形变化规律的过程中，结合数学知识之间的内在联系，通过类比、迁移，可以获得宝贵的数学经验．
【探究1】
如图1，和均为等腰直角三角形，，连接，，且点，，在同一条直线上，则=______°；
【探究2】
如图2，和均为等腰直角三角形，，连接，，延长交于点，则=______°
【探究3】
如图3，和均为等腰三角形，，，连接，，延长交于点，若，则=______°（用含的式子表示）
【探究4】
如图4，和均为等腰三角形，，，连接，，延长交的延长线于点，若，则=______°
（第22题）
23．（本题满分8分）
如图，在四边形中，两条对角线相交于点，，垂足为点，，垂足为点，，点，分别是，的中点，连接，，，．
（第23题）
（1）求证：；
（2）从下列条件中任选一个作为已知条件后，试判断四边形的形状，并证明你的结论．
①，②．
选择的条件：______（填写序号）．
（注：如果选择①，②分别进行解答，按第一个解答计分）
24．（本题满分10分）
“活力海洋之都，精彩宜人之城”，青岛获评2023年中国十大旅游目的地必去城市．为宣传青岛城市文化，某景区研发出一款文创纪念品，投入景区内进行销售．已知该文创纪念品每件的成本为20元，销售一段时间发现，每天的销售量（件）与销售单价（元/件）之间的关系如图所示，图象是直线的一部分．
（1）求与之间的函数关系式；
（2）该景区要想使这种文创纪念品的销售利润每天达到6000元，每件文创纪念品的定价应为多少元？
（3）若规定该文创纪念品的利润率不得高于60%，当销售单价定为多少元时，每天的获利最大？最大利润是多少？
（第24题）
25．（本题满分12分）
如图1，在矩形中，，，点从点出发，沿方向匀速运动，速度为2cm/s；同时，点从点出发，沿方向匀速运动，速度为1cm/s．过点作，交于点，连接，，设运动时间为，请解答下列问题：
（第25题）
（1）当为何值时，？
（2）设的面积为，求与之间的函数关系式；
（3）在运动过程中，是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由；
（4）如图2，点为的中点，连接，当为等腰三角形时，请直接写出的值．
2023—2024学年度第一学期阶段性学情检测
九年级数学试题参考答案及评分标准
说明：
1．如果考生的解法与本解法不同，可参照本评分标准制定相应评分细则．
2．当考生的解答在某一步出现错误，影响了后继部分时，如果这一步以后的解答未改变这道题的内容和难度，可视影响程度决定后面部分的给分，但不得超过后面部分应给分数的一半；如果这一步以后的解答有较严重的错误，就不给分．
3．为阅卷方便，本解答中的推算步骤写得较为详细，但允许考生在解答过程中，合理省略非关键性的推算步骤．
4．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
一、选择题（本大题共10小题，每小题3分，共30分）
二、填空题（本大题共6小题，每小题3分，共18分）
11．50412．13．3
14．15．－116．3：2
三、作图题（本大题满分4分）
作图
结论
四、解答题（本大题共8小题，共68分）
18．（本题共2小题，每小题4分，满分8分）
（1），
（2）由题意得
又∵
∴
∴且
19．（本题满分6分）
解：
一共有9种等可能的结果，其中两次抽出的卡片上的图案都是“宸宸”的结果有1种．
（两次抽出的卡片上的图案都是“宸宸”）=
20．（本题满分8分）
解：过点作，垂足为，过点作，垂足为由题意可得
（第20题）
∴四边形为矩形
∴，
在中
，
∴，
在中
，（）
∴，（）
∵
∴
∴
∴，（）
∴（）
答：该小区北门与南门之间的距离为481（473）米．
（备注：学生使用不同三角函数求得的数值只要符合要求均为正确答案）
21．（本题满分8分）
（1）把代入可得
解得
∴反比例函数的关系式为
点和点的坐标分别为，
把，代入得
解得
∴一次函数的关系式为
（2）
22．（本题满分8分）
【探究1】90
【探究2】90
【探究3】
【探究4】60
23．（本题满分8分）
（1）∵，
∴
又∵，
∴
∴
∵点，分别是，的中点
∴，
∴
（第23题）
（2）选择的条件①
四边形是矩形
∵，
∴四边形是平行四边形
在中，，
∴
∴
∵点是的中点
∴
∴
∴
∴平行四边形是矩形
选择的条件②
四边形是矩形
∵，
∴四边形是平行四边形
∵
∴
∵点是的中点
∴
∴
∴平行四边形是矩形
24．（本题满分10分）
（1）设函数关系式为
把和代入可得
解得
∴与之间的函数关系式为
（2）
解得，
∴该景区要想使这种文创纪念品的销售利润每天达到6000元，每件文创纪念品的定价应为40元或80元．
（3）由题意得
解得
设每天获得的利润为
∵
∴抛物线开口向下
∵对称轴为直线
∴当时，随的增大而增大
∴当时，取得最大值，最大值为
答：当销售单价定为32元时，每天的获利最大，最大利润是4080元．
25．（本小题满分12分）
（1）由题意可得，
∴
∵四边形是矩形
∴，
当时，
∴四边形是平行四边形
∴
∵
∴即
解得
∴
解得
∴当时，．
（2）
=
=
=
∴与t之间的函数关系式为．
（3）假设存在合题意的
解得
∴在运动过程中，当时，．
（4）或
（注：写出其中任意一个答案得2分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
A
C
C
B
A
D
D
B