




最新高考数学一轮复习【讲通练透】 第01讲 导数的概念与运算(三大题型)(讲通)
展开2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题。错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
第01讲 导数的概念与运算
目录
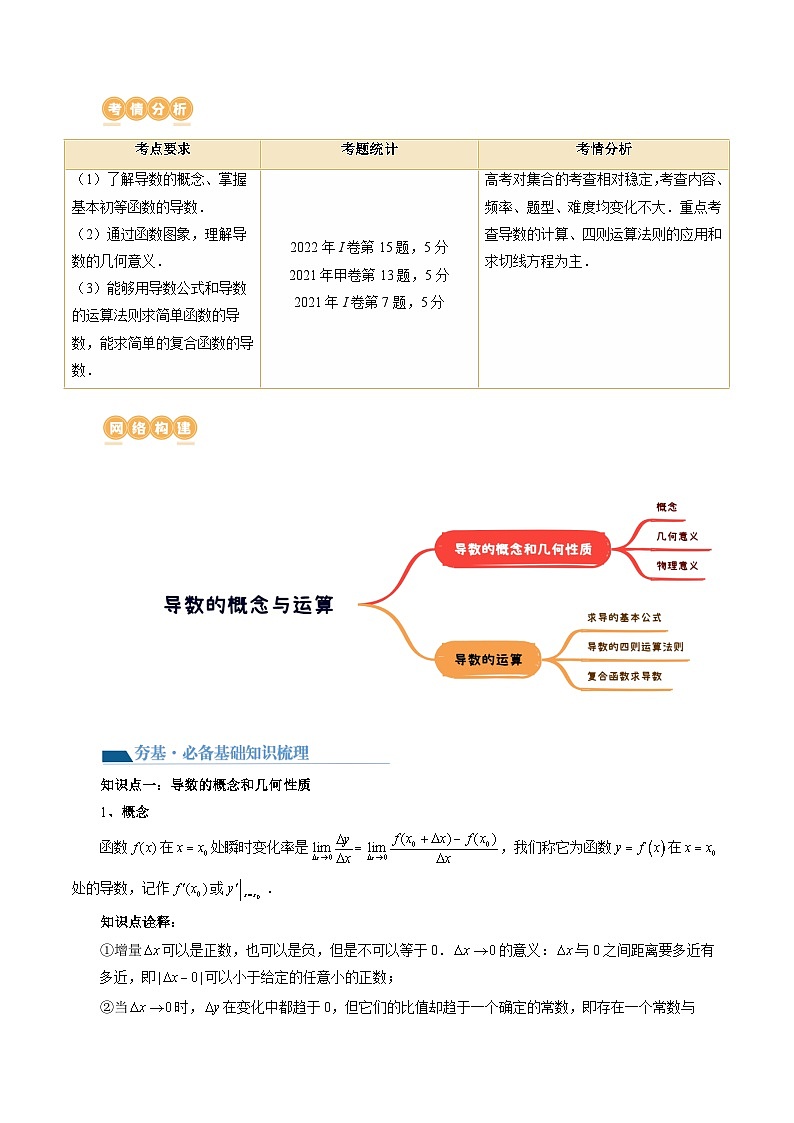
知识点一:导数的概念和几何性质
1、概念
函数在处瞬时变化率是,我们称它为函数在处的导数,记作或.
知识点诠释:
①增量可以是正数,也可以是负,但是不可以等于0.的意义:与0之间距离要多近有
多近,即可以小于给定的任意小的正数;
②当时,在变化中都趋于0,但它们的比值却趋于一个确定的常数,即存在一个常数与
无限接近;
③导数的本质就是函数的平均变化率在某点处的极限,即瞬时变化率.如瞬时速度即是位移在这一时
刻的瞬间变化率,即.
2、几何意义
函数在处的导数的几何意义即为函数在点处的切线的斜率.
3、物理意义
函数在点处的导数是物体在时刻的瞬时速度,即;在点的导数是物体在时刻的瞬时加速度,即.
知识点二:导数的运算
1、求导的基本公式
2、导数的四则运算法则
(1)函数和差求导法则:;
(2)函数积的求导法则:;
(3)函数商的求导法则:,则.
3、复合函数求导数
复合函数的导数和函数,的导数间关系为:
【解题方法总结】
1、在点的切线方程
切线方程的计算:函数在点处的切线方程为,抓住关键.
2、过点的切线方程
设切点为,则斜率,过切点的切线方程为:,
又因为切线方程过点,所以然后解出的值.(有几个值,就有几条切线)
注意:在做此类题目时要分清题目提供的点在曲线上还是在曲线外.
题型一:导数的定义
【例1】(2023·全国·高三专题练习)已知函数的图象如图所示,函数的导数为,则( )
A.B.
C.D.
【对点训练1】(2023·云南楚雄·高三统考期末)已知某容器的高度为20cm,现在向容器内注入液体,且容器内液体的高度h(单位:cm)与时间t(单位:s)的函数关系式为,当时,液体上升高度的瞬时变化率为3cm/s,则当时,液体上升高度的瞬时变化率为( )
A.5cm/sB.6cm/sC.8cm/sD.10cm/s
【对点训练2】(2023·河北衡水·高三衡水市第二中学期末)已知函数的导函数是,若,则( )
A.B.1C.2D.4
【对点训练3】(2023·全国·高三专题练习)若函数在处可导,且,则( )
A.1B.C.2D.
【对点训练4】(2023·高三课时练习)若在处可导,则可以等于( ).
A.B.
C.D.
【解题方法总结】
对所给函数式经过添项、拆项等恒等变形与导数定义结构相同,然后根据导数定义直接写出.
题型二:求函数的导数
【例2】(2023·全国·高三专题练习)求下列函数的导数.
(1);
(2);
(3)
(4);
【对点训练5】(2023·高三课时练习)求下列函数的导数:
(1);
(2);
(3);
(4);
(5);
(6).
【对点训练6】(2023·海南·统考模拟预测)在等比数列中,,函数,则__________.
【对点训练7】(2023·辽宁大连·育明高中校考一模)已知可导函数,定义域均为,对任意满足,且,求__________.
【对点训练8】(2023·河南·高三校联考阶段练习)已知函数的导函数为,且,则______.
【对点训练9】(2023·全国·高三专题练习)已知函数,则__________.
【解题方法总结】
对所给函数求导,其方法是利用和、差、积、商及复合函数求导法则,直接转化为基本函数求导问题.
题型三:导数的几何意义
方向1、在点P处切线
【例3】(2023·广东广州·统考模拟预测)曲线在点处的切线方程为__________.
【对点训练10】(2023·全国·高三专题练习)曲线在点处的切线方程为______.
【对点训练11】(2023·全国·高三专题练习)已知函数,为的导函数.若的图象关于直线x=1对称,则曲线在点处的切线方程为______
【对点训练12】(2023·湖南·校联考模拟预测)若函数是奇函数,则曲线在点处的切线方程为______.
方向2、过点P的切线
【对点训练13】(2023·江西·校联考模拟预测)已知过原点的直线与曲线相切,则该直线的方程是______.
【对点训练14】(2023·浙江金华·统考模拟预测)已知函数,过点存在3条直线与曲线相切,则实数的取值范围是___________.
【对点训练15】(2023·浙江绍兴·统考模拟预测)过点作曲线的切线,写出一条切线方程:__________.
【对点训练16】(2023·海南海口·校联考模拟预测)过轴上一点作曲线的切线,若这样的切线不存在,则整数的一个可能值为_________.
【对点训练17】(2023·全国·模拟预测)过坐标原点作曲线的切线,则切点的横坐标为___________.
【对点训练18】(2023·广西南宁·南宁三中校考模拟预测)若过点有条直线与函数的图象相切,则当取最大值时,的取值范围为__________.
【对点训练19】(2023·全国·模拟预测)已知函数,其导函数为,则曲线过点的切线方程为______.
方向3、公切线
【对点训练20】(2023·云南保山·统考二模)若函数与函数的图象存在公切线,则实数a的取值范围为( )
A.B.
C.D.
【对点训练21】(2023·宁夏银川·银川一中校考二模)若直线与曲线相切,直线与曲线相切,则的值为___________.
【对点训练22】(2023·河北邯郸·统考三模)若曲线与圆有三条公切线,则的取值范围是____.
【对点训练23】(2023·湖南长沙·湖南师大附中校考模拟预测)若曲线和曲线恰好存在两条公切线,则实数a的取值范围为__________.
【对点训练24】(2023·江苏南京·南京师大附中校考模拟预测)已知曲线与曲线有且只有一条公切线,则________.
【对点训练25】(2023·福建南平·统考模拟预测)已知曲线和曲线有唯一公共点,且这两条曲线在该公共点处有相同的切线l,则l的方程为________.
方向4、已知切线求参数问题
【对点训练26】(2023·江苏·校联考模拟预测)若曲线有两条过的切线,则a的范围是______.
【对点训练27】(2023·山东聊城·统考三模)若直线与曲线相切,则的最大值为( )
A.0B.1C.2D.
【对点训练28】(2023·重庆·统考三模)已知直线y=ax-a与曲线相切,则实数a=( )
A.0B.C.D.
【对点训练29】(2023·海南·校联考模拟预测)已知偶函数在点处的切线方程为,则( )
A.B.0C.1D.2
【对点训练30】(2023·全国·高三专题练习)已知是曲线上的任一点,若曲线在点处的切线的倾斜角均是不小于的锐角,则实数的取值范围是( )
A.B.C.D.
【对点训练31】(2023·全国·高三专题练习)已知,,直线与曲线相切,则的最小值是( )
A.16B.12C.8D.4
方向5、切线的条数问题
【对点训练32】(2023·河北·高三校联考阶段练习)若过点可以作曲线的两条切线,则( )
A.B.C.D.
【对点训练33】(2023·全国·高三专题练习)若过点可以作曲线的两条切线,则( )
A.B.C.D.
【对点训练34】(2023·湖南·校联考二模)若经过点可以且仅可以作曲线的一条切线,则下列选项正确的是( )
A.B.C.D.或
方向6、切线平行、垂直、重合问题
【对点训练35】(2023·全国·高三专题练习)若函数与的图象有一条公共切线,且该公共切线与直线平行,则实数( )
A.B.C.D.
【对点训练36】(2023·全国·高三专题练习)已知直线与曲线相交于,且曲线在处的切线平行,则实数的值为( )
A.4B.4或-3C.-3或-1D.-3
【对点训练37】(2023·江西抚州·高三金溪一中校考开学考试)已知曲线在点处的切线互相垂直,且切线与轴分别交于点,记点的纵坐标与点的纵坐标之差为,则( )
A.B.
C.D.
【对点训练38】(2023·全国·高三专题练习)若函数的图象上存在两条相互垂直的切线,则实数的值是( )
A.B.C.D.
【对点训练39】(2023·上海闵行·高三上海市七宝中学校考期末)若函数的图像上存在两个不同的点,使得在这两点处的切线重合,则称为“切线重合函数”,下列函数中不是“切线重合函数”的为( )
A.B.
C.D.
【对点训练40】(2023·全国·高三专题练习)已知A,B是函数,图象上不同的两点,若函数在点A、B处的切线重合,则实数a的取值范围是( )
A.B.C.D.
方向7、最值问题
【对点训练41】(2023·全国·高三专题练习)设点在曲线上,点在曲线上,则最小值为( )
A.B.
C.D.
【对点训练42】(2023·全国·高三专题练习)设点在曲线上,点在曲线上,则的最小值为( )
A.B.
C.D.
【对点训练43】(2023·全国·高三专题练习)设点在曲线上,点在曲线上,则的最小值为( )
A.B.
C.D.
【对点训练44】(2023·全国·高三专题练习)已知实数,,,满足,则的最小值为( )
A.B.8C.4D.16
【对点训练45】(2023·全国·高三专题练习)设函数,其中,.若存在正数,使得成立,则实数的值是( )
A.B.C.D.1
【对点训练46】(2023·宁夏银川·银川二中校考一模)已知实数满足,,则的最小值为( )
A.B.C.D.
【对点训练47】(2023·四川成都·川大附中校考二模)若点是曲线上任意一点,则点到直线距离的最小值为( )
A.B.C.D.
方向8、牛顿迭代法
【对点训练48】(2023·湖北咸宁·校考模拟预测)英国数学家牛顿在17世纪给出一种求方程近似根的方法一Newtn-Raphsn methd译为牛顿-拉夫森法.做法如下:设是的根,选取作为的初始近似值,过点做曲线的切线:,则与轴交点的横坐标为,称是的一次近似值;重复以上过程,得的近似值序列,其中,称是的次近似值.运用上述方法,并规定初始近似值不得超过零点大小,则函数的零点一次近似值为( )(精确到小数点后3位,参考数据:)
A.2.207B.2.208C.2.205D.2.204
【对点训练49】(多选题)(2023·安徽芜湖·统考模拟预测)牛顿在《流数法》一书中,给出了高次代数方程根的一种解法.具体步骤如下:设是函数的一个零点,任意选取作为的初始近似值,过点作曲线的切线,设与轴交点的横坐标为,并称为的1次近似值;过点作曲线的切线,设与轴交点的横坐标为,称为的2次近似值.一般地,过点()作曲线的切线,记与轴交点的横坐标为,并称为的次近似值.对于方程,记方程的根为,取初始近似值为,下列说法正确的是( )
A.B.切线:
C.D.
【对点训练50】(多选题)(2023·全国·模拟预测)牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法一牛顿法.首先,设定一个起始点,如图,在处作图象的切线,切线与轴的交点横坐标记作:用替代重复上面的过程可得;一直继续下去,可得到一系列的数,,,…,,…在一定精确度下,用四舍五入法取值,当,近似值相等时,该值即作为函数的一个零点.若要求的近似值(精确到0.1),我们可以先构造函数,再用“牛顿法”求得零点的近似值,即为的近似值,则下列说法正确的是( )
A.对任意,
B.若,且,则对任意,
C.当时,需要作2条切线即可确定的值
D.无论在上取任何有理数都有
【对点训练51】(2023·全国·高三专题练习)牛顿迭代法(Newtn's methd)又称牛顿–拉夫逊方法(Newtn–Raphsnmethd),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设是的根,选取作为初始近似值,过点作曲线的切线,与轴的交点的横坐标(),称是的一次近似值,过点作曲线的切线,则该切线与轴的交点的横坐标为,称是的二次近似值.重复以上过程,直到的近似值足够小,即把作为的近似解.设,,,,构成数列.对于下列结论:
①();
②();
③;
④().
其中正确结论的序号为__________.
【解题方法总结】
函数在点处的导数,就是曲线在点处的切线的斜率.这里要注意曲线在某点处的切线与曲线经过某点的切线的区别.(1)已知在点处的切线方程为.(2)若求曲线过点的切线方程,应先设切点坐标为,由过点,求得的值,从而求得切线方程.另外,要注意切点既在曲线上又在切线上.
1.(2021·全国·统考高考真题)若过点可以作曲线的两条切线,则( )
A.B.
C.D.
2.(2020·全国·统考高考真题)若直线l与曲线y=和x2+y2=都相切,则l的方程为( )
A.y=2x+1B.y=2x+C.y=x+1D.y=x+
3.(2020·全国·统考高考真题)函数的图像在点处的切线方程为( )
A.B.
C.D.考点要求
考题统计
考情分析
(1)了解导数的概念、掌握基本初等函数的导数.
(2)通过函数图象,理解导数的几何意义.
(3)能够用导数公式和导数的运算法则求简单函数的导数,能求简单的复合函数的导数.
2022年I卷第15题,5分
2021年甲卷第13题,5分
2021年I卷第7题,5分
高考对集合的考查相对稳定,考查内容、频率、题型、难度均变化不大.重点考查导数的计算、四则运算法则的应用和求切线方程为主.
基本初等函数
导函数
(为常数)
2024年高考数学一轮复习讲练测(新教材新高考)第01讲 导数的概念与运算(练习)(原卷版+解析): 这是一份2024年高考数学一轮复习讲练测(新教材新高考)第01讲 导数的概念与运算(练习)(原卷版+解析),共21页。
2024年高考数学一轮复习讲练测(新教材新高考)第01讲 导数的概念与运算(讲义)(原卷版+解析): 这是一份2024年高考数学一轮复习讲练测(新教材新高考)第01讲 导数的概念与运算(讲义)(原卷版+解析),共53页。试卷主要包含了概念,几何意义,物理意义,已知切线求参数问题,切线的条数问题,切线平行,最值问题,牛顿迭代法等内容,欢迎下载使用。
(课标全国版)高考数学第一轮复习讲练测 第12讲 导数的概念及运算(讲+练)原卷版+解析: 这是一份(课标全国版)高考数学第一轮复习讲练测 第12讲 导数的概念及运算(讲+练)原卷版+解析,文件包含课标全国版高考数学第一轮复习讲练测第12讲导数的概念及运算练原卷版+解析docx、课标全国版高考数学第一轮复习讲练测第12讲导数的概念及运算讲原卷版+解析docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。













