山东省济宁市梁山县2023-2024学年九年级上学期期末数学试题

这是一份山东省济宁市梁山县2023-2024学年九年级上学期期末数学试题，共14页。试卷主要包含了精心选一选，相信自己的判断力！等内容，欢迎下载使用。

友情提示：
亲爱的同学，这份试卷将展示你的学识与才华，记录你的智慧与收获，相信你独特的思考、个性化的体验、富有创意的表达一定是最棒的！
你将要解答的这份试题分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，36分，第Ⅱ卷为非选择题，84分，试题满分120分，考试时间为120分钟．
第Ⅰ卷每小题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，须先用橡皮擦干净，再涂改其他答案．第Ⅱ卷在答题卡上作答，答题时按照题目顺序在各题目的答题区域内作答．考试时，不允许使用计算器．
另外，答题前请务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目、座号等填写（涂）准确吆！
第Ⅰ卷（选择题 共36分）
一、精心选一选，相信自己的判断力！（本题共12小题，每小题3分）
注意可以用各种不同的方法来解决你面前的选择题哦！
1．若关于方程是一元二次方程，则的取值范围是（ ）
A．B．C．D．
2．将抛物线向左平移1个单位长度，再向上平移3个单位长度，得到的抛物线的解析式为（ ）
A．B．C．D．
3．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．如图，黑白棋子摆成的图案里下一黑棋，黑棋落在（ ）号位置上使棋子构成的图形既是轴对称图形也是中心对称图形．
A．1B．2C．3D．4
4．下列事件中，属于随机事件的是（ ）
A．抛掷1枚骰子，出现6点向上B．任意画一个三角形，其内角和是
C．抛物线关于轴成轴对称D．圆内接四边形的对角互补
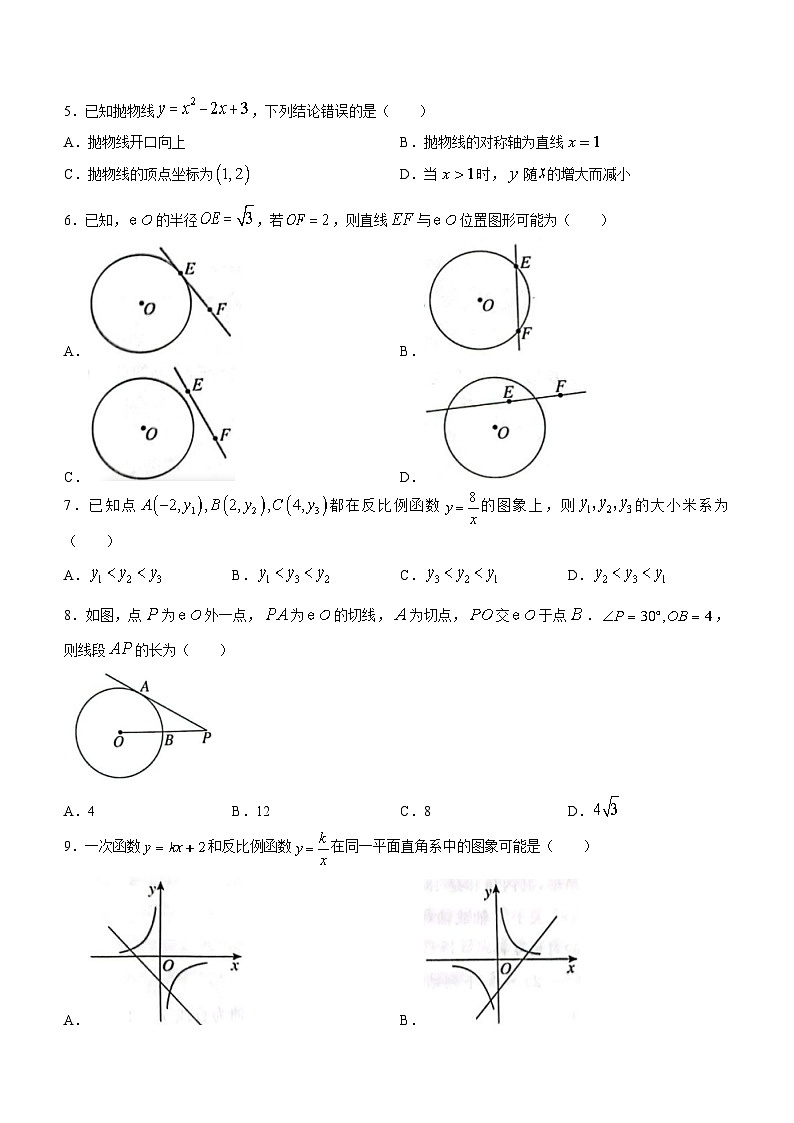
5．已知抛物线，下列结论错误的是（ ）
A．抛物线开口向上B．抛物线的对称轴为直线
C．抛物线的顶点坐标为D．当时，随的增大而减小
6．已知，的半径，若，则直线与位置图形可能为（ ）
A．B．
C．D．
7．已知点都在反比例函数的图象上，则的大小米系为（ ）
A．B．C．D．
8．如图，点为外一点，为的切线，为切点，交于点．，则线段的长为（ ）
A．4B．12C．8D．
9．一次函数和反比例函数在同一平面直角系中的图象可能是（ ）
A．B．
C．D．
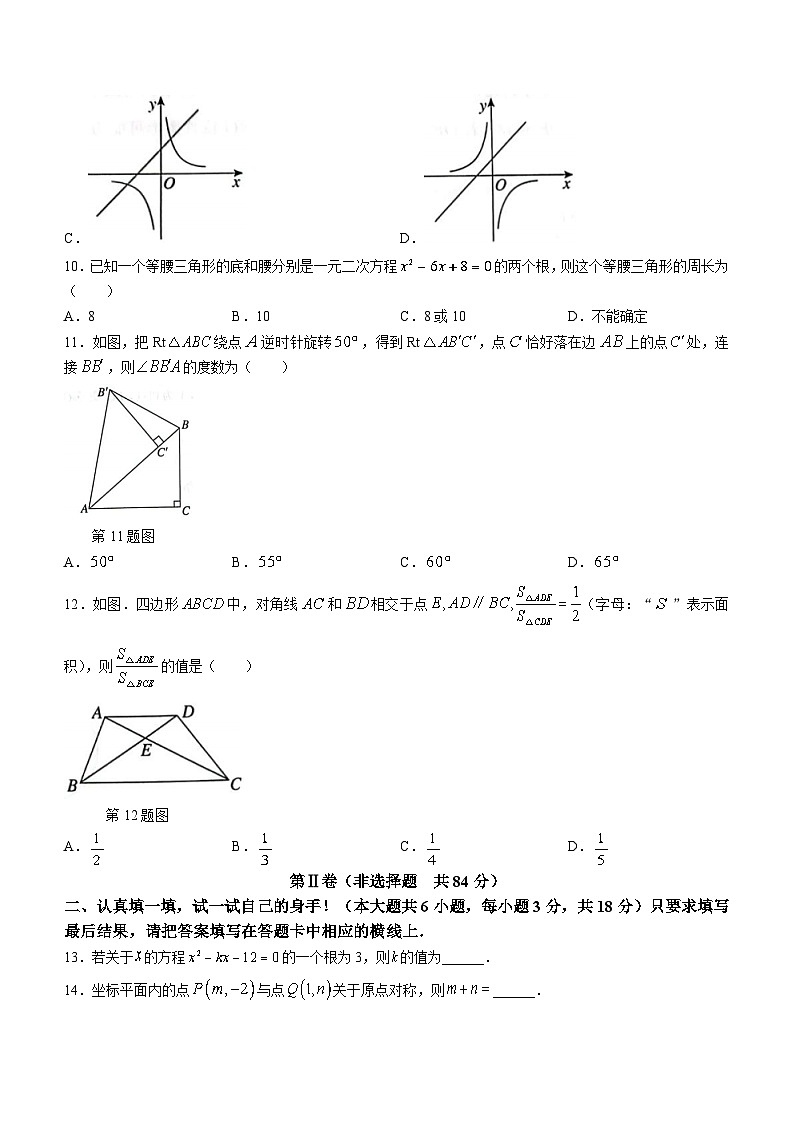
10．已知一个等腰三角形的底和腰分别是一元二次方程的两个根，则这个等腰三角形的周长为（ ）
A．8B．10C．8或10D．不能确定
11．如图，把Rt绕点逆时针旋转，得到Rt，点恰好落在边上的点处，连接，则的度数为（ ）
第11题图
A．B．C．D．
12．如图．四边形中，对角线和相交于点（字母：“”表示面积），则的值是（ ）
第12题图
A．B．C．D．
第Ⅱ卷（非选择题 共84分）
二、认真填一填，试一试自己的身手！（本大题共6小题，每小题3分，共18分）只要求填写最后结果，请把答案填写在答题卡中相应的横线上．
13．若关于的方程的一个根为3，则的值为______．
14．坐标平面内的点与点关于原点对称，则______．
15．如图，在扇形中，，则阴影部分的面积是______．
第15题图
16．如图，设在小孔口前处有一支长的蜡烛经小孔形成的像，恰好照在距小孔后面处的屏幕上，则像的长______．
第16题图
17．如图，反比例函数的图象与直线交于点与轴交于点，轴于点，连接，则的值为______．
第17题图
18．已知函数的大致图象如图所示，如果方程（为实数）有2个不相等的实数根，则的取值范围是______．
三、专心解一解（本大题共8小题，满分66分）请认真读题，冷静思考．解答题应写出文字说明、证明过程或演算步骤．
19．（本题满分7分）
关于的一元二次方程．
（1）若方程有实数根，求实数的取值范围；
（2）设分别是方程的两个根，且满足，求实数的值．
20．（本题满分6分）
如图，的三个顶点坐标分别是．
（1）将先向左平移4个单位长度，再向上平移2个单位长度，得到，画出；
（2）与关于原点成中心对称，画出．
21．（本题满分7分）
如图，是的直径，是的一条弦，且于，连接．
（1）求证：；
（2）若，求的半径的长．
22．（本题满分8分）
2022年虎年新春，中国女足3:2逆转韩国，时隔16年再夺亚洲杯总冠军；2022年国庆，中国女篮高歌猛进，时隔28年再夺世界杯亚军，展现了中国体育的风采！为了培养青少年人才储备，梁山某初中开展了“阳光体育活动”，决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了一些学生（每名学生必选且只能选择这五项活动中的一种）．根据以下统计图提供的信息，请解答下列问题：
（1）本次被调查的学生有______名；补全条形统计图；
（2）学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛，请用画树状图法分析甲和乙同学同时被选中的概率．
23．（本题满分8分）
商场销售一批名牌衬衫，平均每天可售出40件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，前场平均每天可多售出4件．
（1）若商场平均每天要盈利2400元，每件衬衫应降价多少元？
（2）若该商场要每天盈利最大，每件衬衫应降价多少元？盈利最大是多少元？
24．（本题满分9分）
已知一次函数与反比例函数的图象交于两点．
（1）求一次函数和反比例函数的表达式；
（2）求的面积；
（3）结合图象直接写出不等式的解集．
25．（本题满分9分）
如图，是的外接圆，是的直径，点是的中点，过点的切线与的延长线交于点．
（1）求证：；
（2）若的半径为，求的长．
26．（本题满分12分）
已知抛物线．
（1）当抛物线经过点时，
①求抛物线的解析式；
②如果是抛物线上两点（点在点的左侧），且两点之间的水平距离为2，请求出这两点纵坐标之和的最大值；
（2）当二次函数的自变量满足时，函数有最大值为7，求的值．
请再仔细检查一下，也许你会做的更好，考试成功的秘诀在于把会做的题做对，祝你成功！
2023-2024上学期末
九年级参考答案
一、（每小题3分）1．A 2．C 3．B 4．A 5.D 6．A
7．B 8．D 9．C 10．B 11．D 12．C
二、（每小题3分，共18分）
13． 14．1 15. 16．14
17. 5 18．m＝0或m＞4
三、解答题
19．（7分）
解：（1）由题意有△=[﹣（2m﹣1）]2﹣4（m2+1）≥0，
解得m≤﹣，
所以实数m的取值范围是m≤﹣；
（2）由根与系数的关系得：x1+x2=2m﹣1，x1•x2=m2+1，
∵x12+x22=x1x2+10，
∴（x1+x2）2﹣2x1•x2=x1x2+10，
∴（2m﹣1）2﹣3（m2+1）=10，
∴m2﹣4m﹣12=0，
解得m1=6，m2=﹣2，
∵m≤﹣，
∴m=6舍去，
∴m=﹣2．
20．（6分）
（1）为所求；
（2）为所求．

21．（7分）
（1）证明：
∵AB是⊙O的直径，CD⊥AB，
=．
∴∠A=∠2．
又∵OA=OC，
∴∠1=∠A．
∴∠1＝∠2．
（2）∵AB为⊙O的直径，弦CD⊥AB，CD=6
∴∠CEO＝90º，CE＝ED＝3．
设⊙O的半径是R，EB=2，则OE=R-2
∵在Rt△OEC中，
解得：
∴⊙O的半径是．
22．（8分）
（1） 100
补全条形统计图如下：

（2）画树状图如下：

共有12种等可能的结果，其中甲和乙同学同时被选中的结果有2种，
∴甲和乙同学同时被选中的概率为．
23．（8分）
解：（1）设每件衬衫应降价x元
由题意得：
整理得：，即
解得：或
因为商场的目标是扩大销售，增加盈利，尽快减少库存
所以
答：每件衬衫应降价20元；
（2）设每件衬衫应降价x元时，平均每天利润为w元，则
由题意得：
由二次函数的性质可知：当时，w随x的增大而增大；当时，w随x的增大而减小
则当时，w有最大值为2500元
答：每件衬衫降价15元时，商场平均每天盈利最多，每天最多盈利2500元.
24．（9分）
（1）解：∵反比例函数y的图象经过点A（﹣3，2），
∴m＝﹣3×2＝﹣6，
∵点B（1，n）在反比例函数图象上，
∴n＝﹣6．
∴B（1，﹣6），
把A，B的坐标代入y＝kx+b，则，
解得k＝﹣2，b＝﹣4，
∴一次函数的解析式为y＝﹣2x﹣4，反比例函数的解析式为y；
（2）解：如图，设直线AB交y轴于C，
则C（0，﹣4），
∴S△AOB＝S△OCA+S△OCB4×34×1＝8；
（3）解：观察函数图象知，
不等式kx+b的解集为x＜﹣3或0＜x＜1．
25.（9分）
（1）证明：连接OB，如图所示：

∵是⊙O的切线，
∴，
∴．
∵点B是的中点，
∴，
∴．
∵，
∴，
∴，
∴，
即．
（2）解：过点O作，如图所示：

∵，
∴.
∵，
∴四边形为矩形，
∴
∴．
26.（12分）
（1）解：①抛物线经过点，
，
，
抛物线的解析式为；
②,是抛物线上两点(点在点的左侧)，且两点之间的水平距离为2，
设，则，
，
，
当时，，两点纵坐标之和的最大值为5；
（2）解：二次函数的对称轴为直线，
当时，
自变量满足时，函数有最大值为7，
当时，函数取得最大值，
，
；
当时，
自变量满足时，函数有最大值为7，
当时，函数取得最大值，
，
．
当时，
自变量满足时，函数有最大值为，
当时，函数取得最大值，
，
解得：，均不符合题意，舍去，
综上：的值为4或．