北京市西城区2023-2024学年八年级上学期期末数学试卷

这是一份北京市西城区2023-2024学年八年级上学期期末数学试卷，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.火纹是一种常见的装饰图案，多用于建筑、家具设计等.下列火纹图案中，可以看成处轴对称图形的是( )
A. B.
C. D.
2.下列运算中，正确的是( )
A. x8÷x2=x4B. (x3)4=x7C. (−2x3)3=−8x9D. x4+x=x5
3.在平面直角坐标系xOy中，点P(−2,3)关于x轴的对称点坐标是( )
A. (−2,−3)B. (2,−3)C. (2,3)D. (−3,−2)
4.下列各式从左到右变形一定正确的是( )
A. xy=x2y2B. −x−yx+y=−1C. xy=x+zy+zD. x+yx2−y2=1x+y
5.如图，在△ABC中，∠A=90°，∠C=30°，BD是△ABC的角平分线.若点D到BC的距离为3，则AC的长为( )
A. 12B. 7.5C. 9D. 6
6.如果a2−3a−7=0，那么代数式(a−1)2+a(a−4)−2的值为( )
A. −15B. −8C. 6D. 13
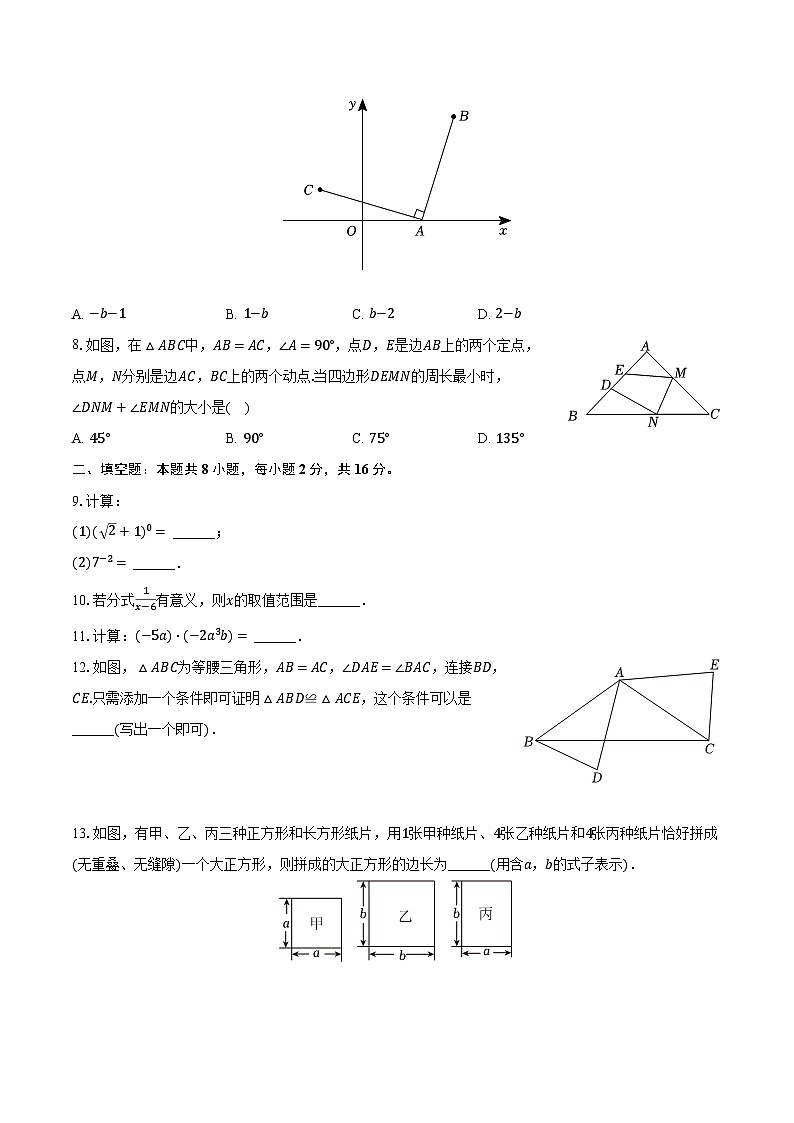
7.如图，在平面直角坐标系xOy中，已知点A(2,0)，B(3,b)(b>0)，AC⊥AB且AC=AB，则点C的横坐标为( )
A. −b−1B. 1−bC. b−2D. 2−b
8.如图，在△ABC中，AB=AC，∠A=90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点.当四边形DEMN的周长最小时，∠DNM+∠EMN的大小是( )
A. 45°B. 90°C. 75°D. 135°
二、填空题：本题共8小题，每小题2分，共16分。
9.计算：
(1)( 2+1)0= ______；
(2)7−2= ______．
10.若分式1x−6有意义，则x的取值范围是______．
11.计算：(−5a)⋅(−2a3b)= ______．
12.如图，△ABC为等腰三角形，AB=AC，∠DAE=∠BAC，连接BD，CE.只需添加一个条件即可证明△ABD≌△ACE，这个条件可以是______(写出一个即可)．
13.如图，有甲、乙、丙三种正方形和长方形纸片，用1张甲种纸片、4张乙种纸片和4张丙种纸片恰好拼成(无重叠、无缝隙)一个大正方形，则拼成的大正方形的边长为______(用含a，b的式子表示)．
14.甲、乙两名同学作为志愿者帮助图书馆清点一批图书，甲3h清点完这批图书的13，乙加入清点剩余的图书，两人合作2.4h清点完剩余的图书.如果乙单独清点这批图书需要几小时？若设乙单独清点这批图书需要xh，则根据题意可列方程为______．
15.在正三角形纸片ABC上按如图方式画一个正五边形DEFGH，其中点F，G在边BC上，点E，H分别在边AB，AC上，则∠BEF的大小是______°.
16.如图，动点C与线段AB构成△ABC，其边长满足AB=9，CA=2a+2，CB=2a−3.点D在∠ACB的平分线上，且∠ADC=90°，则a的取值范围是______，△ABD的面积的最大值为______．
三、解答题：本题共10小题，共84分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
分解因式：
(1)xy3−xy；
(2)2x2−20x+50．
18.(本小题11分)
(1)计算：(a−3b)(2a+b)；
(2)先化简，再求值：(a−2+2a−a2a+2)÷a−2a2+4a+4，其中a=32．
19.(本小题8分)
如图，点C，D在AB上，AC=BD，EA=FB，∠A=∠B，ED，FC相交于点G．
(1)求证：∠ADE=∠BCF；
(2)求证：EG=FG．
20.(本小题7分)
解方程：6x+1=xx+3．
21.(本小题9分)
已知：如图，∠AOB．
求作：射线OC，使∠AOC=3∠AOB，且点C在直线OA的下方．
作法：①在射线OA上取一点P，过点P作射线OA的垂线，与射线OB相交于点M；
②在MP的延长线上取一点N，使PN=PM；
③以点O为圆心，OM长为半径画弧，再以点M为圆心，MN长为半径画弧，两弧在直线OA下方相交于点C；
④作射线OC．
所以射线OC即为所求作的射线．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连接ON，CM．
∵PM⊥OA，PN=PM，
∴ON=OM.(______)(填推理的依据)
∴∠ ______=2∠POM．
∵OC=OM，
∴OC=ON．
在△OCM和△ONM中，
OC=ONOM=OM=，( )
∴△OCM≌△ONM.(______)(填推理的依据)
∴∠ ______=∠NOM．
∴∠AOC=∠POM+∠COM=3∠POM，
即∠AOC=3∠AOB．
22.(本小题8分)
阅读材料：
如果整数x，y满足x=a2+b2，y=c2+d2，其中a，b，c，d都是整数，那么一定存在整数m，n，使得xy=m2+n2．
例如，25=32+42，40=22+62，25×40=302+(−10)2或25×40=182+262，…
根据上述材料，解决下列问题：
(1)已知5=12+22，74=52+72，5×74=192+32或5×74=m2+172，…
若m>0，则m= ______；
(2)已知41=42+52，y=c2+d2(c,d为整数)，41y=m2+n2.若m=5c−4d，求n(用含c，d的式子表示)；
(3)一般地，上述材料中的m，n可以用含a，b，c，d的式子表示，请直接写出一组满足条件的m，n(用含a，b，c，d的式子表示)．
23.(本小题9分)
在△ABC中，AB2a−3①2a−3+9>2a+2②2a+2+2a−3>9③，
不等式①②显然成立，
由③得：a>2.5；
延长AD交CB延长线于M，过M作MH⊥AB交AB延长线于H，
∵CD平分∠ACB，
∴∠MCD=∠ACD，
∵∠ADC=90°，
∴∠CDM=180°−90°=90°，
∴∠ADC=∠MDC，
∵CD=CD，∠MCD=∠ACD，
∴△ACD≌△MCD(ASA)，
∴AD=MD，CM=AC=2a+2，
∴BM=CM−BC=5，
∵S△ABD=12S△ABM，
∴当△ABM的面积最大时，△ABD的面积最大，
∵△ABM的面积=12AB⋅MH，AB=9，MH≤MB=5，
∴△ABD面积的最大值=12×9×5×12=454．
故答案为：a>2.5，454．
由三角形三边关系定理得到2a+2+9>2a−3①2a−3+9>2a+2②2a+2+2a−3>9③，即可求出a>2.5；延长AD交CB延长线于M，由ASA证明△ACD≌△MCD，推出AD=MD，CM=AC=2a+2，得到BM=CM−BC=5，又S△ABD=12S△ABM，因此当△ABM的面积最大时，△ABD的面积最大，而AB=9，MH≤MB=5，即可求出△ABD的面积的最大值．
本题考查三角形三边关系，全等三角形的判定和性质，垂线段最短，三角形的面积，关键是掌握三角形三边关系定理，构造全等三角形．
17.【答案】解：(1)原式=xy(y2−1)=xy(y+1)(y−1)；
(2)原式=2(x2−10x+25)
=2(x−5)2．
【解析】(1)提取公因式后利用平方差公式分解即可；
(2)原式提取公因式，再利用完全平方公式分解即可．
此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
18.【答案】解：(1)(a−3b)(2a+b)
=2a2+ab−6ab−3b2
=2a2−5ab−3b2；
(2)(a−2+2a−a2a+2)÷a−2a2+4a+4
=(a−2)(a+2)+2a−a2a+2⋅(a+2)2a−2
=2a−4a+2⋅(a+2)2a−2
=2(a−2)a+2⋅(a+2)2a−2
=2(a+2)
=2a+4，
当a=32时，原式=2×32+4=3+4=7．
【解析】(1)利用多项式乘多项式的法则进行计算，即可解答；
(2)先利用异分母分式加减法法则计算括号里，再算括号外，然后把a的值代入化简后的式子进行计算即可解答．
本题考查了分式的化简求值，多项式乘多项式，准确熟练地进行计算是解题的关键．
19.【答案】证明：(1)∵AC=BD，
∴AD=BC，
在△ADE和△BCF中，
AD=BC∠A=∠BAE=BF，
∴△ADE≌△BCF(SAS)，
∴∠ADE=∠BCF；
(2)∵△ADE≌△BCF，
∴DE=CF，∠ADE=∠BCF，
∴DG=CG，
∴EG=FG．
【解析】(1)由全等三角形的性质可得△ADE≌△BCF，可得∠ADE=∠BCF；
(2)由全等三角形的性质可得△ADE≌△BCF，可得DE=CF，∠ADE=∠BCF，可证DG=CG，即可求解．
本题考查了全等三角形的判定与性质，掌握全等三角形的判定方法是解题的关键．
20.【答案】解：原方程去分母得：6(x+3)+x(x+3)=x2，
去括号得：6x+18+x2+3x=x2，
移项，合并同类项得：9x=−18，
系数化为1得：x=−2，
经检验，x=−2是分式方程的解，
故原方程的解为x=−2．
【解析】利用解分式方程的步骤解方程即可．
本题考查解分式方程，熟练掌握解方程的方法是解题的关键．
21.【答案】线段的垂直平分线上的点到线段的两个端点的距离相等 MON SSS MOC
【解析】(1)解：图形如图所示：
(2)证明：连接ON，CM．
∵PM⊥OA，PN=PM，
∴ON=OM(线段的垂直平分线上的点到线段的两个端点的距离相等)，
∴∠MON=2∠POM．
∵OC=OM，
∴OC=ON．
在△OCM和△ONM中，
OC=ONOM=OMMC=MN，
∴△OCM≌△ONM(SSS)，
∴∠MOC=∠NOM．
∴∠AOC=∠POM+∠COM=3∠POM，
即∠AOC=3∠AOB．
故答案为：线段的垂直平分线上的点到线段的两个端点的距离相等，MON，MC=MN，SSS，MOC．
(1)根据要求作出图形；
(2)证明△OCM≌△ONM(SSS)，推出∠MOC=∠NOM，可得结论．
本题考查作图−复杂作图，全等三角形的判定和性质等知识，解题的关键是学会构造全等三角形解决问题．
22.【答案】9
【解析】解：(1)∵5×74=m2+172，
∴370=m2+289．
∴m2=81，
∵m>0，
∴m=9．
故答案为：9．
(2)∵41y=m2+n2，m=5c−4d，y=c2+d2，
∴41(c2+d2)=(5c−4d)2+n2．
∴41c2+41d2=25c2−40cd+16d2+n2．
∴n2=16c2+40cd+25d2．
∴n2=(4c+5d)2．
∴n=4c+5d或n=−4c−5d．
(3)∵x=a2+b2，y=c2+d2，xy=m2+n2，
∴(a2+b2)(c2+d2)=m2+n2．
∴a2c2+a2d2+b2c2+b2d2=m2+n2．
∴(a2c2+b2d2)+(a2d2+b2c2)=m2+n2．
∴(a2c2+b2d2+2abcd)+(a2d2+b2c2−2abcd)=m2+n2．
∴(ac+bd)2+(ad−bc)2=m2+n2．
∴m和n的一组值为：m=ac+bd，n=ad−bc(答案不唯一)．
(1)5×74=370，172=289，那么m2=370−289=81，根据m>0可得m的值；
(2)把41y=m2+n2中的m和y换掉，整理，可得n2的值，进而可得n的值；
(3)把xy=m2+n2.中的x和y换掉，整理得到两个完全平方式相加等于m2+n2的形式，得到m和n的一组值即可．
本题考查因式分解的应用．把所给等式整理成含有完全平方式的形式是解决本题的关键．用到的知识点为：a2±2ab+b2=(a±b)2；两个数的平方相等，那么这两个数相等或互为相反数．
23.【答案】(1)解：①∵BE⊥AC，
∴∠AEB=∠DEC=90°，
∵∠DBA=∠DCA，AC=CD，
∴△ABE≌△DCE(AAS)，
∴AE=DE，
∴∠DAE=∠ADE=45°；
②AC=2DE+BD．
理由：∵△ABE≌△DCE，
∴BE=CE，AE=DE，
∴AC=AE+CE=DE+DE+BD=2DE+BD；
(2)证明：过点F作FG⊥AM，交AM的延长线于点G，过点C作CH⊥AM于点H，过点A作AN⊥BD，交BD的延长线于点N，过点D作DK⊥AC于点K，

∵∠ABD=∠DCA，∠DKC=∠ANB=90°，AB=CD，
∴△ABN≌△DCK(AAS)，
∴AN=DK，
又∵AD=DA，
∴Rt△ADN≌Rt△DAK(HL)，
∴∠ADN=∠DAK，
∵∠ADN=∠FDG，
∴∠FDG=∠DAK，
∵M为CF的中点，
∴CM=FM，
∵∠CMH=∠FMG，∠CHM=∠FGM，
∴△CMH≌△FMG(AAS)，
∴CH=FG，
∵∠AHC=∠G=90°，
∴△ACH≌△DFG(AAS)，
∴AC=DF．
【解析】(1)①证明△ABE≌△DCE(AAS)，由全等三角形的性质得出AE=DE，则可得出答案；
②由全等三角形的性质得出BE=CE，AE=DE，则可得出结论；
(2)过点F作FG⊥AM，交AM的延长线于点G，过点C作CH⊥AM于点H，过点A作AN⊥BD，交BD的延长线于点N，过点D作DK⊥AC于点K，证明△ABN≌△DCK(AAS)，得出AN=DK，证明Rt△ADN≌Rt△DAK(HL)，得出∠ADN=∠DAK，证明△CMH≌△FMG(AAS)，由全等三角形的性质得出CH=FG，证明△ACH≌△DFG(AAS)，由全等三角形的性质得出AC=DF．
本题是三角形的综合题，考查了全等三角形的判定与性质，等腰直角三角形的性质，平行线的性质，熟练掌握全等三角形的判定与性质是解题的关键．
24.【答案】H、K
【解析】解：(1)当t=1时，A(2,1)，B(5,1)，
∴AB=3，
∵四边形ABCD为正方形，
∴C(2,4)，D(5,4)，
①设点(x,y)是图形N的“双称图形”，
第一次对称后的坐标为(−x,y)，
第二次对称轴的坐标为(2+x,y)，
∴2≤2+x≤5，1≤y≤4，
∴0≤x≤3，1≤y≤4，
∴H和K是图形N的“双称图形”，
故答案为：H、K；
②由①可知，E2(2+m,2)，F2(m+4,2)，G2(m+3,3)，
当△E2F2G2与正方形ABCD有交点时，
m+4≥12+m≤5，
∴−3≤m≤3；
(2)设点(x,y)是图形N的“双称图形”，
第一次对称后的坐标为(−x,y)，
第二次对称轴的坐标为(2t+x,y)，
∴A2(4t,1)，B2(4t+3,1)，C2(4t,4)，D2(4t+3,1)，
∵正方形ABCD和正方形A2B2C2D2有交点，
∴4t≤2t+34t+3≥2t，
∴−32≤t≤32．
(1)由于两条对称轴都垂直于x轴，所以经过两次对称变化后，点的纵坐标不变；根据正方形的性质，写出A，B，C，D的坐标；
①设点(x,y)是图形N的“双称图形”，根据两次对称变化的坐标变化，求出x，y的取值范围，然后判断H，R，K是否是图形N的“双称图形”；
②根据①得出的x，y的变化规律，求出E，F，G的两次对称后的坐标，然后判断当两次对称后的三角形与正方形有交点时m的取值即可；
(2)根据(1)中两次对称后坐标的变化规律，得出A，B，C，D两次对称后的坐标，然后根据两个正方形有交点求出t的取值范围即可．
本题主要考查了四边形的综合题，根据对称的性质得出坐标变化规律是本题解题的关键．
25.【答案】2 ②④
【解析】解：(1)如图1，∵EF⊥BD于点F，
∴∠DFE=∠BFE=90°，
∵∠EDF=45°，
∴∠DEF=∠EDF=45°，
∴FD=FE，
∵△ABC是等边三角形，点D在BC延长线上，BE平分∠ABD，
∴∠ABD=60°，
∴∠ABE=∠DBE=12∠ABD=30°，
∴FE=12BE，
∴BEFD=BEFE=2，
故答案为：2．
(2)如图1，∵BE=2FE，DE= FD2+FE2= 2FE，
∴BE≠DE，
∴点E不在BD的垂直平分线上，
∴点E不一定在BD的垂直平分线上，
故①错误；
如图2，连接CE，∵AB=CB，BE平分∠ABC，
∴BE垂直平分AC，
∴AE=CE，
∵点E在AD的垂直平分线上，
∴AE=DE，
∴CE=DE，
∵EF⊥CD于点F，
∴CF=DF，
∴点F是线段CD的中点，
故②正确；
如图3，连接AF，
∵DF=BC=AC，CF=DF，∠BAC=∠ACB=60°，
∴CF=AC=BC，
∴∠CFA=∠CAF，
∴∠ACB=∠CFA+∠CAF=2∠CAF=60°，
∴∠CAF=30°，
∴∠BAF=∠BAC+∠CAF=90°，
∴AB⊥AF，
∴AD与AD不垂直，
故③错误；
如图2，∵∠BFE=90°，∠FBE=30°，
∴∠BEF=90°−∠FBE=60°，
∵BE垂直平分AC，
∴AE=CE，
∴∠AEB=∠CEB，
∴∠AEC=2∠CEB，
∵CE=DE，EF⊥CD，
∴∠DEF=∠CEF，
∴∠DEC=2∠CEF，
∴∠AED=∠AEC+∠DEC=2(∠CEB+∠CEF)=2∠BEF=120°，
∴点D运动过程中，∠AED的大小始终不变，
故④正确，
故答案为：②④．
(1)由EF⊥BD于点F，得∠DFE=∠BFE=90°，则∠DEF=∠EDF=45°，所以FD=FE，由△ABC是等边三角形，BE平分∠ABD，得∠ABE=∠DBE=12∠ABD=30°，则FE=12BE，所以BEFD=BEFE=2，于是得到问题的答案；
(2)当∠EDF=45°时，由BE=2FE，DE= FD2+FE2= 2FE，得BE≠DE，则点E不在BD的垂直平分线上，可判断①错误；连接CE，由AB=CB，BE平分∠ABC，得BE垂直平分AC，则AE=CE，因为点E在AD的垂直平分线上，所以AE=DE，则CE=DE，所以点F是线段CD的中点，可判断②正确；连接AF，可证明CF=AC=BC，则∠CFA=∠CAF=30°，所以∠BAF=90°，则AB⊥AF，所以AD与AD不垂直，可判断③错误；由∠BFE=90°，∠FBE=30°，得∠BEF=60°，再证明∠AEC=2∠CEB，∠DEC=2∠CEF，则∠AED=2∠BEF=120°，可判断④正确，于是得到问题的答案．
此题重点考查等边三角形的性质、等腰直角三角形的判定与性质、线段的垂直平分线的性质、三角形的一个外角等于与它不相邻的两个内角的和、直角三角形的两个锐角互余等知识，此题综合性强，难度较大，属于考试压轴题．
26.【答案】18 17
【解析】解：(1)∵2−0=|0−2|，
∴d(A,B)=5×2+4×2=18，
∵2−0